Геометрия расстояния

редактировать

Геометрия расстояния - это характеристика, а изучение устанавливает точек на основе только при заданных значениях расстояний между парами элементов. Говоря более абстрактно, это исследование полуметрических пространств и изометрических преобразований между ними. С этой точки зрения, его можно рассматривать как предмет в рамках общей топологии.

Исторически первым результатом в геометрии расстояний является формула Герона в 1 веке нашей эры. Современная теория началась в 19 веке с работ Артура Кэли, за которыми последовали более обширные разработки в 20-м веке Карлом Менгером и другими.

Проблемы с геометрией расстояния возникают всякий раз, когда нужно вывести форму конфигурации точек (относительные положения ) по расстояниям между ними, например, в биологии, сенсорная сеть, съемка, навигация, картография и физика.

Содержание

1 Введение и определения
- 1.1 Первая проблема: гиперболическая навигация
- 1.2 Вторая проблема: уменьшение размерности
- 1.3 Определения
  - 1.3.1 Полиметрическое пространство
  - 1.3.2 Изометрическое вложение
  - 1.3.3 Аффинная независимость
2 Кэли –Детерминанты Менгера
3 История
4 Теорема Менгера о характеризации
5 Характеризация с помощью определителей Кэли – Менгера
- 5.1 Вложение $n + 1 {\ displaystyle n + 1}$ $n + 1$ точек в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$
- 5.2 Встраивание $n + 2 {\ displaystyle n + 2}$ $n + 2$ и $n + 3 {\ displaystyle n + 3}$ $n+3$ точек
- 5.3 Встраивание произвольного количества точек
6 Приложения
7 См. также
8 Ссылка ces

Введение и определения

Концепции дистанционной геометрии сначала будут объяснены путем описания двух конкретных проблем.

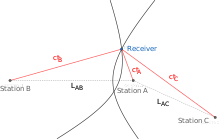
Проблема гиперболической навигации

Первая проблема: гиперболическая навигация
Рассмотрим три наземные радиостанции A, B, C, местоположение которых известно. Радиоприемник находится в неизвестном месте. Время, необходимое для прохождения радиосигнала от станций до приемника, $t A, t B, t C {\ displaystyle {\ displaystyle t_ {A}, t_ {B}, t_ {C}}}$ ${\ displaystyle {\ displaystyle t_ {A}, t_ {B}, t_ {C}}}$ , неизвестны, но разница во времени, $t A - t B {\ displaystyle {\ displaystyle t_ {A} -t_ {B}}}$ ${\ displaystyle {\ displaystyle t_ {A} -t_ {B}}}$ и $t A - t C {\ displaystyle {\ displaystyle t_ {A} -t_ {C}}}$ ${\ displaystyle {\ displaystyle t_ {A} -t_ {C }}}$ , известны. По ним можно узнать разницу расстояний $c (t A - t B) {\ displaystyle c ({\ displaystyle t_ {A} -t_ {B}})}$ ${\ displaystyle c ({\ displaystyle t_ {A} -t_ {B}}) }$ и $c (t A - t C) {\ displaystyle c ({\ displaystyle t_ {A} -t_ {C}})}$ ${\ displaystyle c ({\ displaystyle t_ {A} -t_ {C}})}$ , из которого можно определить положение получателя.

Вторая проблема: уменьшение размерности
В анализе данных часто дается список данных, представленных в виде векторов $v = (x 1, ⋯, xn) ∈ R n {\ displaystyle \ mathbf {v} = (x_ {1}, \ cdots, x_ {n}) \ in \ mathbb {R} ^ {n}}$ ${\ displaystyle \ mathbf {v} = (x_ {1}, \ cdots, x_ {n}) \ in \ mathbb {R} ^ {n}}$ , и нужно выяснить, лежат ли они в аффинном подпространстве малой размерности. Низкоразмерное представление данных имеет множество преимуществ, таких как экономия места для хранения, времени вычислений и лучшего понимания данных.

Определения

Теперь мы формализуем некоторые определения, которые естественным образом возникают при рассмотрении наших проблем.

Полиметрический интервал

Дан список точек на $R = {P 0, ⋯, P n} {\ displaystyle R = \ {P_ {0}, \ cdots, P_ {n} \}}$ ${\ dis стиль воспроизведения R = \ {P_ {0}, \ cdots, P_ {n} \}}$ , $n ≥ 0 {\ displaystyle n \ geq 0}$ $n \ geq 0$ , мы можем произвольно указать расстояния между парами точек списком $dij>0 {\ displaystyle d_ {ij}>0}$ $d_{ij}>0$ , $0 ≤ i < j ≤ n {\displaystyle 0\leq i$ ${\ displaystyle 0 \ leq i <j \ leq n}$ . Это определяет полуметрическое пространство : метрическое пространство без неравенства треугольника.

Явно мы определяем полуметрическое пространство как непустое множество $R {\ displaystyle R}$ $R$ с полуметрическим $d: R × R → [0, ∞) {\ displaystyle d: R \ times R \ to [ 0, \ infty)}$ ${\ displaystyle d: R \ times R \ to [ 0, \ infty)}$ такая, что для всех $x, y ∈ R {\ displaystyle x, y \ in R}$ $x, y \ in R$ ,

Положительность: $d (x, y) = 0 {\ displaystyle d (x, y) = 0}$ $d (x, y) = 0$ тогда и только тогда, когда $x = y {\ displaystyle x = y}$ $x = y$ .
Симметрия: $d (x, y) = d (y, x) {\ d isplaystyle d (x, y) = d (y, x)}$ $d (x, y) = d (y, x)$ .

Любое метрическое пространство a fortiori является полуметрическим пространством. В частности, $R k {\ displaystyle \ mathbb {R} ^ {k}}$ $\ mathbb {R} ^ {k}$ , $k {\ displaystyle k}$ $k$ -мерный евклидово space, это каноническое метрическое пространство в дистанционной геометрии.

Неравенство треугольника опущено в определении, потому что мы не хотим налагать больше ограничений на расстояния $dij {\ displaystyle d_ {ij}}$ $d_ {ij}$ , чем простое требование, чтобы они положительные.

На практике полуметрические пространства естественным образом возникают из-за неточных измерений. Например, для трех точек $A, B, C {\ displaystyle A, B, C}$ $A, B, C$ на линии, где $d AB = 1, d BC = 1, d AC = 2 {\ displaystyle d_ {AB} = 1, d_ {BC} = 1, d_ {AC} = 2}$ ${\ displaystyle d_ {AB} = 1, d_ {BC} = 1, d_ {AC} = 2}$ , неточное измерение может дать $d AB = 0,99, d BC = 0,98, d AC = 2,00 {\ displaystyle d_ {AB} = 0,99, d_ {BC} = 0,98, d_ {AC} = 2,00}$ ${\ displaystyle d_ {AB} = 0,99, d_ {BC} = 0,98, d_ {AC} = 2,00}$ , нарушая неравенство треугольника.

Изометрическое вложение

Даны два полуметрических пространства, $(R, d), (R ′, d ′) {\ displaystyle (R, d), (R ', d')}$ $(R,d),(R',d')$ , изометрическое вложение от $R {\ displaystyle R}$ $R$ до $R ′ {\ displaystyle R '}$ $R'$ - это карта $f: R → R ′ {\ displaystyle f: R \ to R '}$ $f:R\to R'$ , которая сохраняет полуметрическую, то есть для всех $x, y ∈ R { \ Displaystyle х, у \ в R}$ $x, y \ in R$ , $d (х, у) = d '(е (х), е (у)) {\ Displaystyle d (х, у) = d' (е (х), f (y))}$ $d(x,y)=d'(f(x),f(y))$ .

Например, с учетом конечного полуметрического пространства $(R, d) {\ displaystyle (R, d)}$ ${\ displaystyle (R, d) }$ , определенного выше, изометрическое вложение в определяется следующим образом: точек $A 0, A 1,…, A n ∈ R k {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {k }}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {k}}}$ , такое, что $d (A i, A j) = dij {\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$ ${\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$ для всех $0 ≤ i < j ≤ n {\displaystyle 0\leq i$ ${\ displaystyle 0 \ leq i <j \ leq n}$ .

Аффинная независимость

Даны точки $A 0, A 1,…, A n ∈ R k {\ textstyle A_ {0}, A_ { 1}, \ ldots, A_ {n} \ in {\ di splaystyle \ mathbb {R} ^ {k}}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {k}}}$ , они определены как аффинно независимые, если и только если они не могут поместиться в один $l {\ displaystyle l}$ ${\ displaystyle l }$ -мерное аффинное подпространство $R k {\ displaystyle \ mathbb {R} ^ {k}}$ ${\ displaystyle \ mathbb {R} ^ {k}}$ для любого $l < n {\displaystyle l$ ${\ displaystyle l <n}$ , если $n {\ displaystyle n}$ $n$ -симплекс они охватывают, $vn {\ displaystyle v_ {n}}$ $v_ {n}$ , имеет положительный $n {\ displaystyle n}$ $n$ -volume, то есть $V oln (vn)>0 {\ displaystyle Vol_ {n} (v_ {n})>0}$ $Vol_{n}(v_{n})>0$ .

В общем, когда $k ≥ n {\ displaystyle k \ geq n}$ ${\ displaystyle k \ geq n}$ , они аффинно независимы, поскольку общий n-симплекс невырожден. Например, 3 точки на плоскости, как правило, не коллинеарны, потому что треугольник, который они охватывают, не вырождается в отрезок прямой. Точно так же 4 точки в пространстве, как правило, не компланарны, потому что тетраэдр, который они охватывают, не вырождается в плоский треугольник.

Когда $n>k {\ displaystyle n>k}$ $n>k$ , они должны быть аффинно зависимыми. Это можно увидеть, отметив, что любые $n {\ displaystyle n}$ $n$ - симплекс, который может поместиться внутри $R k {\ displaystyle \ mathbb {R} ^ {k}}$ $\ mathbb {R} ^ {k}$ , должен быть «плоским».

Определители Кэли – Менгера

Кэли– Определители Менгера, названные в честь Артура Кэли и Карла Менгера, являются определителями матриц расстояний между наборами точек.

Пусть $A 0, A 1,…, A n {\ textstyle A_ { 0}, A_ {1}, \ ldots, A_ {n}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$ быть n + 1 точкой в полуметрическом пространстве, их определитель Кэли – Менгера определяется как

$CM (A 0, ⋯, A n) = | 0 d 01 2 d 02 2 ⋯ d 0 n 2 1 d 01 2 0 d 12 2 ⋯ d 1 n 2 1 d 02 2 d 12 2 0 ⋯ d 2 n 2 1 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ d 0 n 2 d 1 n 2 d 2 n 2 ⋯ 0 1 1 1 1 ⋯ 1 0 | {\ displaystyle CM (A_ {0}, \ cdots, A_ {n}) = {\ begin {vmatrix} 0 d_ {01 } ^ {2} d _ {02} ^ {2} \ cdots d_ {0n} ^ {2} 1 \\ d_ {01} ^ {2} 0 d_ {12} ^ {2} \ cdots d_ {1n} ^ {2} 1 \\ d_ {02} ^ {2} d_ {12} ^ {2} 0 \ cdots d_ {2n} ^ {2} 1 \\\ vdots \ vdots \ vdots \ ddots \ vdots \ vdots \ \ d_ {0n} ^ {2} d_ {1n} ^ {2} d_ {2n} ^ {2} \ cdots 0 1 \\ 1 1 1 \ cdots 1 0 \ end {vmatrix}}}$ ${\ displaystyle CM (A_ {0}, \ cdots, A_ {n}) = { \ begin {vmatrix} 0 d_ {01} ^ {2} d_ {02} ^ {2} \ cdots d_ {0n} ^ {2} 1 \\ d_ {01} ^ {2} 0 d_ { 12} ^ {2} \ cdots d_ {1n} ^ {2} 1 \\ d_ {02} ^ {2} d_ {12} ^ {2} 0 \ cdots d_ {2n} ^ {2} 1 \\ \ vdots \ vdots \ vdots \ ddots \ vdots \ vdots \\ d_ {0n} ^ {2} d_ {1n} ^ {2} d_ {2n} ^ {2} \ cdots 0 1 \\ 1 1 1 \ cdots 1 0 \ end {vmatrix}}}$

Если $A 0, A 1,…, A n ∈ R k {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {k}}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {k}}}$ , то они составляют вершины (возможно, вырожденного ) n-симплекса $vn {\ displaystyle {\ displaystyle v_ {n}}}$ ${\ displaystyle {\ displaystyle v_ {n}}}$ в $Р К {\ Displaystyle \ mathbb {R} ^ {k}}$ $\ mathbb {R} ^ {k}$ . Можно показать, что n-мерный объем симплекса $vn {\ displaystyle {\ displaystyle v_ {n}}}$ ${\ displaystyle {\ displaystyle v_ {n}}}$ удовлетворяет

$V oln (vn) 2 = (- 1) n + 1 (n!) 2 2 n CM (A 0, ⋯, A n) {\ displaystyle Vol_ {n} (v_ {n}) ^ {2} = {\ frac {(-1) ^ {n + 1}} {(n!) ^ {2} 2 ^ {n}}} CM (A_ {0}, \ cdots, A_ {n})}$ ${\ displaystyle Vol_ {n} (v_ {n}) ^ {2} = {\ frac {( -1) ^ {n + 1}} {(n!) ^ {2} 2 ^ {n}}} CM (A_ {0}, \ cdots, A_ {n})}$ .

Обратите внимание, что для случая $n = 0 {\ displaystyle n = 0}$ $n = 0$ , имеем $V ol 0 (v 0) = 1 {\ displaystyle Vol_ {0} (v_ {0}) = 1}$ ${\ displaystyle Vol_ {0} (v_ {0}) = 1}$ , что означает, что «0-мерный объем» 0-симплекса равен 1, то есть в 0-симплексе есть 1 точка.

$A 0, A 1,…, A n {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$ аффинно независимы, если $V oln ( vn)>0 {\ displaystyle Vol_ {n} (v_ {n})>0}$ $Vol_{n}(v_{n})>0$ , то есть $(- 1) n + 1 CM (A 0, ⋯, A n)>0 {\ displaystyle (- 1) ^ {n + 1} CM (A_ {0}, \ cdots, A_ {n})>0}$ $(-1)^{n+1}CM(A_{0},\cdots,A_{n})>0$ . Таким образом, определители Кэли – Менгера предоставляют вычислительный способ доказательства аффинной независимости.

Если $k < n {\displaystyle k$ ${\ displaystyle k <n}$ , то точки должны быть аффинно зависимыми, таким образом $CM (A 0, ⋯, A n) = 0 {\ displaystyle CM (A_ {0}, \ cdots, A_ { n}) = 0}$ ${\ displaystyle CM (A_ {0}, \ cdots, A_ {n}) = 0}$ . В статье Кэли 1841 г. изучается частный случай $k = 3, n = 4 {\ displaystyle k = 3, n = 4}$ ${\ displaystyle k = 3, n = 4}$ , то есть любых 5 точек $A 0, ⋯, A 5 {\ displaystyle A_ {0}, \ cdots, A_ {5}}$ ${\ displaystyle A_ {0}, \ cdots, A_ {5}}$ в трехмерном пространстве должен иметь $CM (A 0, ⋯, A 4) = 0 {\ displaystyle CM (A_ {0}, \ cdots, A_ {4}) = 0}$ ${\ displaystyle CM (A_ {0}, \ cdots, A_ {4}) = 0}$ .

История

Первым результатом дистанционной геометрии является формула Герона из 1 века нашей эры, которая дает площадь треугольника из расстояний между его тремя вершинами. Формула Брахмагупты из 7 века нашей эры обобщает ее на циклические четырехугольники. Тарталья из 16 века нашей эры обобщил его, чтобы дать объем тетраэдра, исходя из расстояний между его четырьмя вершинами.

Современная теория дистанционной геометрии началась с Автора Кэли и Карла Менгера. Кэли опубликовал определитель Кэли в 1841 году, который является частным случаем общего определителя Кэли – Менгера. В 1928 году Менгер доказал характеристическую теорему для всех полуметрических пространств, которые изометрически вложимы в n-мерное евклидово пространство $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ . В 1931 году Менгер использовал отношения расстояния, чтобы дать аксиоматическую трактовку евклидовой геометрии.

Книга Леонарда Блюменталя дает общий обзор дистанционной геометрии на уровне аспирантуры, большая часть которой рассматривается на английском языке для выпускников. первый раз, когда он был опубликован.

характеризационная теорема Менгера

Менгер доказал следующую характеризационную теорему полуметрических пространств:

полуметрическое пространство $(R, d) {\ displaystyle (R, d)}$ ${\ displaystyle (R, d) }$ изометрически встраивается в $n {\ displaystyle n}$ $n$ -мерное евклидово пространство $R n {\ displaystyle \ mathbb {R} ^ {n }}$ $\ mathbb {R} ^ {n}$ , но не в $R m {\ displaystyle \ mathbb {R} ^ {m}}$ $\ mathbb {R} ^ {m}$ для любого $0 ≤ m < n {\displaystyle 0\leq m$ ${\ displaystyle 0 \ leq m <n}$ , если и только если:

$R {\ displaystyle R}$ $R$ содержит $(n + 1) {\ displaystyle (n + 1)}$ $(n+1)$ -точечное подмножество $S {\ displaystyle S}$ $S$ , который является изометрическим с аффинно независимым $(n + 1) {\ displaystyle (n + 1)}$ $(n+1)$ -точечным подмножеством $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ ;
любой $(n + 3) {\ displaystyle (n + 3)}$ ${\ displaystyle (n + 3)}$ -точечное подмножество $S ′ {\ Displaystyle S '}$ $S'$ , полученный добавлением любых двух дополнительных точек $R {\ displaystyle R}$ $R$ к $S {\ displaystyle S}$ $S$ , это конгруэнтно подмножеству точек $(n + 3) {\ displaystyle (n + 3)}$ ${\ displaystyle (n + 3)}$ $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ .

Доказательство этой теоремы в несколько ослабленном виде (для метрических пространств вместо полуметрических пространств) находится в.

Характеризация через определители Кэли – Менгера

В книге Блюметаля доказаны следующие результаты.

Встраивание $n + 1 {\ displaystyle n + 1}$ $n + 1$ точек в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$
Учитывая полуметрическое пространство $(S, d) {\ displaystyle (S, d)}$ ${\ displaystyle (S, d)}$ , где $S = {P 0, ⋯, P n} {\ displaystyle S = \ {P_ {0}, \ cdots, P_ {n} \}}$ ${\ displaystyle S = \ {P_ {0}, \ cdots, P_ {n} \}}$ и $d (P i, P j) = dij ≥ 0 {\ displaystyle d (P_ {i}, P_ {j }) = d_ {ij} \ geq 0}$ ${\ displaystyle d (P_ {i}, P_ {j}) = d_ {ij} \ geq 0 }$ , $0 ≤ i < j ≤ n {\displaystyle 0\leq i$ ${\ displaystyle 0 \ leq i <j \ leq n}$ , изометрическое вложение $(S, d) {\ displaystyle (S, d)}$ ${\ displaystyle (S, d)}$ в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ определяется как $A 0, A 1,…, A n ∈ R n {\ textstyle A_ { 0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {n}}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in {\ displaystyle \ mathbb {R} ^ {n}}}$ , s uch, что $d (A i, A j) = dij {\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$ ${\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$ для всех $0 ≤ i < j ≤ n {\displaystyle 0\leq i$ ${\ displaystyle 0 \ leq i <j \ leq n}$ .

И снова возникает вопрос, существует ли такое изометрическое вложение для $(S, d) {\ displaystyle (S, d)}$ ${\ displaystyle (S, d)}$ .

Необходимое условие легко увидеть: для всех $k = 1, ⋯, n {\ displaystyle k = 1, \ cdots, n}$ ${\ displaystyle k = 1, \ cdots, n}$ , пусть $vk {\ displaystyle v_ {k}}$ $v_ {k}$ будет k-симплексом, образованным $A 0, A 1,…, A k {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {k}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {k}}$ , затем

$(- 1) k + 1 CM (P 0, ⋯, P k) = (- 1) k + 1 CM (A 0, ⋯, A k) = 2 k (k!) k V olk (vk) 2 ≥ 0 {\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) = (- 1) ^ {k + 1} CM (A_ {0}, \ cdots, A_ {k}) = 2 ^ {k} (k!) ^ {K} Vol_ {k} (v_ {k}) ^ {2} \ geq 0}$ ${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) = (- 1) ^ { k + 1} CM (A_ {0}, \ cdots, A_ {k}) = 2 ^ {k} (k!) ^ {k} Vol_ {k} (v_ {k}) ^ {2} \ geq 0 }$

верно и обратное. То есть, если для всех $k = 1, ⋯, n {\ displaystyle k = 1, \ cdots, n}$ ${\ displaystyle k = 1, \ cdots, n}$ ,

$(- 1) k + 1 CM (P 0, ⋯, P k) ≥ 0 {\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0}$ ${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k }) \ geq 0}$ ,

, тогда такое вложение существует.

Кроме того, такое внедрение является уникальным с точностью до изометрии в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ . То есть, учитывая любые два изометрических вложения, определенные как $A 0, A 1,…, A n {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$ , и $A 0 ′, A 1 ′,…, A n ′ {\ textstyle A '_ {0}, A' _ {1}, \ ldots, A '_ {n}}$ ${\textstyle A'_{0},A'_{1},\ldots,A'_{n}}$ существует (не обязательно уникальная) изометрия $T: R n → R n {\ displaystyle T: \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$ ${\ displaystyle T: \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$ , такое, что $T (A k) = A k ′ {\ displaystyle T (A_ {k}) = A '_ {k}}$ $T(A_{k})=A'_{k}$ для всех $k = 0, ⋯, n {\ displaystyle k = 0, \ cdots, n}$ ${\ displaystyle k = 0, \ cdots, n}$ . Такой $T {\ displaystyle T}$ $T$ уникален тогда и только тогда, когда $CM (P 0, ⋯, P n) ≠ 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}) \ neq 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}) \ neq 0}$ , то есть $A 0, A 1,…, A n {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ { n}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$ аффинно независимы.

Встраивание $n + 2 {\ displaystyle n + 2}$ $n + 2$ и $n + 3 {\ displaystyle n + 3}$ $n+3$ точек

Если $n + 2 {\ displaystyle n + 2}$ $n + 2$ очков $P 0, ⋯, P n + 1 {\ displaystyle P_ {0}, \ cdots, P_ {n +1}}$ ${\ displaystyle P_ {0}, \ cdots, P_ {n + 1}}$ может быть встроено в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ как $A 0, ⋯, A n + 1 {\ displaystyle A_ {0}, \ cdots, A_ {n + 1}}$ ${\ displaystyle A_ {0}, \ cdots, A_ {n + 1}}$ , то кроме условий выше, дополнительное необходимое условие состоит в том, что $(n + 1) {\ displaystyle (n + 1)}$ $(n+1)$ -симплекс, образованный $A 0, A 1,…, A n + 1 {\ textstyle A_ {0}, A_ {1}, \ ldots, A_ { n + 1}}$ ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n + 1}}$ , не должно иметь $(n + 1) {\ displaystyle (n + 1)}$ $(n+1)$ -мерного объема. То есть $CM (P 0, ⋯, P n, P n + 1) = 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0 }$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ .

Верно и обратное. То есть, если для всех $k = 1, ⋯, n {\ displaystyle k = 1, \ cdots, n}$ ${\ displaystyle k = 1, \ cdots, n}$ ,

$(- 1) k + 1 CM (P 0, ⋯, P k) ≥ 0 {\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0}$ ${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k }) \ geq 0}$ ,

$CM (P 0, ⋯, P n, P n + 1) = 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ ,

, тогда такое вложение существует.

Для встраивания $n + 3 {\ displaystyle n + 3}$ $n+3$ точек в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ , необходимые и достаточные условия аналогичны:

Для всех $k = 1, ⋯, n {\ displaystyle k = 1, \ cdots, n}$ ${\ displaystyle k = 1, \ cdots, n}$ , $(- 1) k + 1 CM (P 0, ⋯, P k) ≥ 0 {\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0}$ ${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k }) \ geq 0}$ ;
$CM (P 0, ⋯, п N, P N + 1) знак равно 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ ;
$CM (P 0, ⋯, П N, п N + 2) знак равно 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 2}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 2}) = 0}$ ;
$CM (P 0, ⋯, P п, п п + 1, п п + 2) знак равно 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}$ .

Встраивание произвольного числа точек

В общем случае $n + 3 {\ displaystyle n + 3}$ $n+3$ оказывается достаточно.

В общем, учитывая полуметрическое пространство $(R, d) {\ displaystyle (R, d)}$ ${\ displaystyle (R, d) }$ , оно может быть изометрически встроено в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ тогда и только тогда, когда существует $P 0, ⋯, P n ∈ R {\ displaystyle P_ {0}, \ cdots, P_ {n} \ in R}$ ${\ displaystyle P_ {0}, \ cdots, P_ {n} \ in R}$ , такая, что для всех $k = 1, ⋯, n {\ displaystyle k = 1, \ cdots, n}$ ${\ displaystyle k = 1, \ cdots, n}$ , $(- 1) k + 1 CM ( P 0, ⋯, P k) ≥ 0 {\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0}$ ${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k }) \ geq 0}$ и для любого $P n + 1, P n + 2 ∈ R {\ displaystyle P_ {n + 1}, P_ {n + 2} \ in R}$ ${\ displaystyle P_ {n + 1}, P_ {n + 2} \ in R}$ ,

$CM (P 0, ⋯, P n, P n + 1) знак равно 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}$ ;
$CM (P 0, ⋯, P n, P n + 2) знак равно 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 2}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 2}) = 0}$ ;
$CM (P 0, ⋯, P n, P n + 1, P n + 2) = 0 {\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}$ .

И такое вложение уникально вплоть до изометрии в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ .

Кроме того, если $CM (P 0, ⋯, P n) ≠ 0 {\ displaystyle CM (P_ { 0}, \ cdots, P_ {n}) \ neq 0}$ ${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}) \ neq 0}$ , то он не может быть изометрически встроен в любой $R m, m < n {\displaystyle \mathbb {R} ^{m},m$ ${\ displaystyle \ mathbb {R} ^ {m}, m <n}$ . И такое вложение уникально с точностью до уникальной изометрии в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ .

Таким образом, определители Кэли – Менгера дают конкретный способ вычислить, можно ли вложить полуметрическое пространство в $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ , для некоторого конечного $n {\ displaystyle n}$ $n$ , и если да, то какие является минимальным $n {\ displaystyle n}$ $n$ .

Приложения

Существует множество применений геометрии расстояний.

В телекоммуникационных сетях, таких как GPS, известны положения некоторых датчиков (которые называются якорями), а также известны некоторые расстояния между датчиками: проблема состоит в том, чтобы определить положения всех датчиков. Гиперболическая навигация - это одна из технологий, предшествующих GPS, которая использует Геометрия расстояния для определения местоположения судов в зависимости от времени, которое требуется сигналам для достижения якорей.

В химии много применений. Такие методы, как ЯМР, позволяют измерять расстояния между парами атомов данной молекулы, и проблема состоит в том, чтобы вывести трехмерную форму молекулы на основе этих расстояний.

Вот некоторые программные пакеты для приложений:

DGSOL. Решает задачи геометрии на больших расстояниях в макромолекулярном моделировании.
Xplor-NIH. На основе X-PLOR для определения структуры молекул на основе данных экспериментов ЯМР. Он решает проблемы геометрии расстояния с помощью эвристических методов (таких как Simulated Annealing ) и методов локального поиска (таких как Conjugate Gradient Minimization ).
TINKER. Молекулярное моделирование и дизайн. проблемы с геометрией.
SNLSDPclique. Код MATLAB для определения местоположения датчиков в сети датчиков на основе расстояний между датчиками.

См. также

Матрица евклидовых расстояний
Многомерное масштабирование (статистическое метод, используемый при измерении расстояний со случайными ошибками)
Метрическое пространство
Формула Тартальи
Триангуляция
Трилатерация

Ссылки