В физических науках функция Эйри (или функция Эйри первого вида ) Ai (x) - это специальная функция, названная в честь британского астронома Джорджа Бидделла Эйри (1801–1892). Функция Ai (x) и связанная с ней функция Bi (x) являются линейно независимыми решениями дифференциального уравнения

, известное как уравнение Эйри или уравнение Стокса . Это простейшее линейное дифференциальное уравнение второго порядка с точкой поворота (точка, в которой характер решения меняется с колебательного на экспоненциальный).
Функция Эйри является решением не зависящего от времени уравнения Шредингера для частицы, заключенной в треугольной потенциальной яме, и для частицы в одномерной постоянной силе поле. По той же причине он также служит для обеспечения однородных полуклассических приближений вблизи точки поворота в приближении ВКБ, когда потенциал может быть локально аппроксимирован линейной функцией положения. Решение с треугольной потенциальной ямой имеет прямое отношение к пониманию электронов, захваченных в полупроводниковых гетеропереходах.
Функция Эйри также лежит в основе формы интенсивности вблизи оптической направленной каустики, такой как радуга. Исторически именно эта математическая проблема побудила Эйри разработать эту специальную функцию.
A другая функция, также названная в честь Эйри, важна в микроскопии и астрономии ; он описывает шаблон из-за дифракции и интерференции, создаваемых точечным источником света (который намного меньше, чем предел разрешающей способности микроскопа или телескопа ).
Содержание
- 1 Определения
- 2 Свойства
- 3 Асимптотические формулы
- 4 Комплексные аргументы
- 5 Связь с другими специальными функциями
- 6 Преобразование Фурье
- 7 Другие варианты использования термина функция Эйри
- 7.1 Коэффициент пропускания интерферометра Фабри – Перо
- 7.2 Дифракция на круглой апертуре
- 8 История
- 9 См. Также
- 10 Примечания
- 11 Ссылки
- 12 Внешние ссылки
Определения

График Ai (x) красным цветом и Bi (x) синим
Для реальных значений x функция Эйри первого рода может быть определена с помощью несобственный интеграл Римана :

которое сходится по тесту Дирихле. Для любого действительного числа  существует положительное действительное число
существует положительное действительное число  такое, что функция
такое, что функция  - возрастающая, неограниченная и выпуклая с непрерывной и неограниченной производной на интервале
- возрастающая, неограниченная и выпуклая с непрерывной и неограниченной производной на интервале  . Сходимость интеграла на этом интервале может быть доказана с помощью теста Дирихле после замены
. Сходимость интеграла на этом интервале может быть доказана с помощью теста Дирихле после замены  .
.
y = Ai (x) удовлетворяет уравнению Эйри

Это уравнение имеет два линейно независимых решения. С точностью до скалярного умножения Ai (x) является решением, удовлетворяющим условию y → 0 при x → ∞. Стандартным выбором для другого решения является функция Эйри второго рода, обозначаемая Bi (x). Он определяется как решение с той же амплитудой колебаний, что и Ai (x) при x → −∞, которое отличается по фазе на π / 2:
![{\ displaystyle \ operatorname {Bi} (x) = {\ frac {1} {\ pi}} \ int _ {0 } ^ {\ infty} \ left [\ exp \ left (- {\ tfrac {t ^ {3}} {3}} + xt \ right) + \ sin \ left ({\ tfrac {t ^ {3}}) {3}} + xt \ right) \, \ right] dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3bcd1d018bad9c90fe2a8575dbb9038f2371ad4)
Свойства
Значения Ai (x) и Bi (x) и их производные при x = 0 равны

Здесь Γ обозначает гамма-функцию. Отсюда следует, что вронскиан для Ai (x) и Bi (x) равен 1 / π.
Когда x положительный, Ai (x) положительный, выпуклый и экспоненциально убывающий до нуля, тогда как Bi (x) положительный, выпуклый и экспоненциально возрастающий. Когда x отрицателен, Ai (x) и Bi (x) колеблются около нуля с постоянно увеличивающейся частотой и постоянно уменьшающейся амплитудой. Это подтверждается приведенными ниже асимптотическими формулами для функций Эйри.
Функции Эйри ортогональны в том смысле, что

снова с использованием неправильного интеграла Римана.
Асимптотические формулы
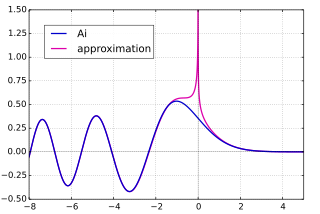
Ai (синий) и синусоидальная / экспоненциальная асимптотика Ai (пурпурный)
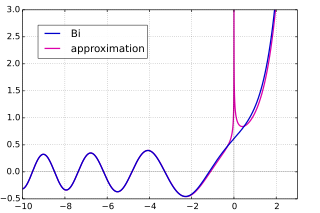
Bi (синий) и синусоидальная / экспоненциальная асимптотика Bi (пурпурный)
Как объяснено ниже, функции Эйри могут быть расширены до комплексной плоскости, давая целые функции. Асимптотика функций Эйри при | z | стремится к бесконечности при постоянном значении arg (z) зависит от arg (z): это называется феноменом Стокса. Для | arg (z) | < π we have the following асимптотическая формула для Ai (z):
![{\ displaystyle \ operatorname {Ai} (z) \ sim {\ dfrac {e ^ {- {\ frac {2} {3} } z ^ {\ frac {3} {2}}}} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0 } ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (n + {\ frac {5} {6}}) \ Gamma (n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {n}} {2 \ pi n! z ^ {3n / 2}}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e89d2a50ade6755bc8c233375d7c8fee8ea4516)
и аналогичный для Bi (z), но применим только когда | arg (z) | < π/3:
![{\ displaystyle \ operatorname {Bi} (z) \ sim {\ frac {e ^ {{\ frac {2} {3}} z ^ { \ frac {3} {2}}}} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {\ Gamma (n + {\ frac {5} {6}}) \ Gamma (n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {n}} {2 \ pi n! Z ^ {3n / 2}}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c08bd4d24ec332406e1c1a96d83002b8e3be44ac)
Более точная формула для Ai (z) и формула для Bi (z), когда π / 3 < |arg(z)| < π or, equivalently, for Ai(−z) and Bi(−z) when |arg(z)| < 2π/3 but not zero, are:
![{\ displaystyle {\ begin {align} \ operatorname {Ai} (-z) \ sim {} {\ frac {\ sin \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4 }} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {( -1) ^ {n} \ Gamma (2n + {\ frac {5} {6}}) \ Gamma (2n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n}} {2 \ pi (2n)! z ^ {3n}}} \ right] \\ [6pt] {} - {\ frac {\ cos \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4}} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1 } {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (2n + {\ frac {11} {6}}) \ Gamma (2n + {\ frac {7} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n + 1}} {2 \ pi (2n + 1)! Z ^ {3n + 3/2}}} \ right] \\ [6pt] \ operatorname {Bi} (-z) \ sim {} {\ frac {\ cos \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4}} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4} }}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (2n + {\ frac {5} {6}}) \ Gamma (2n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n}} {2 \ pi (2n)! z ^ {3n}}} \ right] \\ [6pt] {} + {\ frac {\ sin \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4 }} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (2n + {\ frac {11} {6}}) \ Gamma (2n + {\ frac {7} { 6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n + 1}} {2 \ pi (2n + 1)! Z ^ {3n + 3/2}}} \ right ]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a8b6907a3908d270c8d98fa305880b40caee7b)
Когда | arg (z) | = 0 это хорошие приближения, но они не являются асимптотическими, потому что соотношение между Ai (−z) или Bi (−z) и указанным выше приближением стремится к бесконечности, когда синус или косинус стремится к нулю. Также доступны асимптотические расширения для этих пределов. Они перечислены в (Abramowitz and Stegun, 1954) и (Olver, 1974).
Также можно получить асимптотические выражения для этих производных Ai '(z) и Bi' (z). Как и раньше, когда | arg (z) | <π:
![{\displaystyle \operatorname {Ai} '(z)\sim -{\dfrac {z^{\frac {1}{4}}e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d491607498d24f9877d42607185e408a784e8e51)
Когда | arg (z) | <π/3 we have:
![{\displaystyle \operatorname {Bi} '(z)\sim {\frac {z^{\frac {1}{4}}e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56643de7b1a34d11f96e74847567dfbe63f56c9f)
Аналогично, выражение для Ai '(- z) и Bi' (- z), когда | arg ( z) | < 2π/3 but not zero, are
![{\displaystyle {\begin{aligned}\operatorname {Ai} '(-z)\sim {}-{\frac {z^{\frac {1}{4}}\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]{}-{\frac {z^{\frac {1}{4}}\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\[6pt]\operatorname {Bi} '(-z)\sim {}{\frac {z^{\frac {1}{4}}\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]{}-{\frac {z^{\frac {1}{4}}\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/297bf831c84b567992feda77bcee4d67e8093ac0)
Комплексные аргументы
Мы можем расширить определение функции Эйри на комплексную плоскость с помощью

где интеграл ведется по пути C, начинающемуся в бесконечно удаленной точке с аргументом −π / 3 и заканчивающемуся в бесконечно удаленной точке с аргументом π / 3. В качестве альтернативы мы можем использовать дифференциальное уравнение y ′ ′ - xy = 0, чтобы расширить Ai (x) и Bi (x) до целых функций на комплексной плоскости.
Асимптотическая формула для Ai (x) все еще действительна в комплексной плоскости, если взято главное значение x и x отделен от отрицательной действительной оси. Формула для Bi (x) верна, если x находится в секторе {x ∈ C : | arg (x) | < (π/3)−δ} for some positive δ. Finally, the formulae for Ai(−x) and Bi(−x) are valid if x is in the sector {x ∈ C : | arg (x) | < (2π/3)−δ}.
Из асимптотического поведения функций Эйри следует, что и Ai (x), и Bi (x) имеют бесконечное количество нулей на отрицательной действительной оси. Функция Ai (x) не имеет других нулей в комплексной плоскости, а функция Bi (x) также имеет бесконечно много нулей в секторе {z ∈ C : π / 3 < |arg(z)| < π/2}.
Plots
![{\ displaystyle \ Re \ left [\ operatorname {Ai} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92d14f4ea89c98289bdd7724aa97a65bc37be26c) | ![{\ displaystyle \ Im \ left [\ operatorname {Ai} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f188455d8f10f38330bed9927837e68fdbc9df46) |  | ![{\ displaystyle \ operatorname {arg } \ left [\ operatorname {Ai} (x + iy) \ right] \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2722a1be5b008fee5231676bfbecc9a6a15f6da) |
|---|
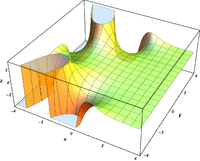 |  |  |  |
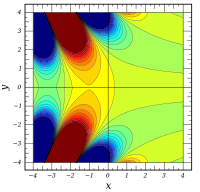 | 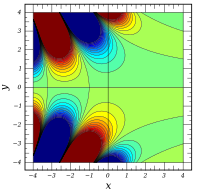 |  |  |
![{\ displaystyle \ Re \ left [\ operatorname {Bi} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2dd29c05abcff762111d663f165d7c1055d3de) | ![{\ displaystyle \ Im \ left [\ operatorname {Bi} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/456ed57b8b06b7da31229c0cb6989b24c2d9b3d8) |  | ![{\ displaystyle \ operatorname {arg} \ left [\ operatorname {Bi} (x + iy) \ right] \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef422f3f85b66c485cf5b87ffa8b57b1b3e254a1) |
|---|
 |  | 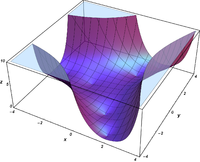 | 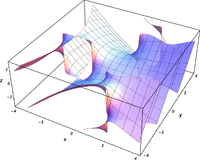 |
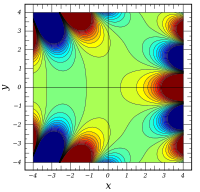 |  | 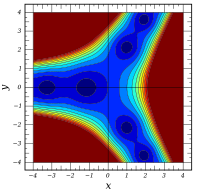 | 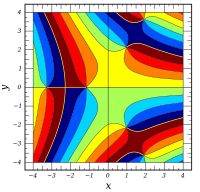 |
Связь с другими специальными функциями
Для положительных аргументов функции Эйри связаны с модифицированными функциями Бесселя :

Здесь I ± 1/3 и K 1/3 - решения

Первая производная функции Эйри равна

Функции K 1/3 и K 2/3 могут быть представлены в терминах быстро сходящихся интегралов (см. также модифицированные функции Бесселя )
Для отрицательных аргументов функция Эйри связана с функциями Бесселя :

Здесь J ± 1/3 - решения

Функции счетчика Hi (x) и -Gi (x) решают уравнение y ′ ′ - xy = 1 / π. Их также можно выразить через функции Эйри:

преобразование Фурье
Используя определение функции Эйри Ai (x), несложно показать ее преобразование Фурье определяется как

Другие варианты использования термина функция Эйри
Коэффициент пропускания интерферометра Фабри – Перо

«функция Эйри» в смысле пропускания интерферометра Фабри-Перо
Функция пропускания интерферометра Фабри-Перо также называется функцией Эйри :

где обе поверхности имеют коэффициент отражения R и

- коэффициент ловкости.
Дифракция на круглой апертуре

«Функция Эйри» в смысле дифракции на круглой апертуре.
Независимо, в третьем значении термина, форма диска Эйри, возникающий в результате дифракции волны на круглой апертуре, иногда также обозначается как функция Эйри (см., Например, здесь ). Этот вид функции тесно связан с функцией Бесселя.
История
Функция Эйри названа в честь британского астронома и физика. Джордж Бидделл Эйри (1801–1892), который столкнулся с этим в своем раннем исследовании оптики в физике (Airy 1838). Обозначение Ai (x) было введено Гарольдом Джеффрисом. Эйри стал британским королевским астрономом в 1835 году и занимал этот пост до своего выхода на пенсию в 1881 году.
См. Также
- Использовано доказательство гипотезы Виттена матричнозначное обобщение функции Эйри.
- дзета-функция Эйри
Примечания
Ссылки
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. "Глава 10". Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое издание оригинала с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 446. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Эйри (1838), «Об интенсивности света вблизи каустика», Труды Кембриджского философского общества, University Press, 6 : 379–402, Bibcode : 1838TCaPS... 6..379A
- Фрэнк Уильям Джон Олвер (1974). Асимптотика и специальные функции, Глава 11. Academic Press, New York.
- Press, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, BP (2007), «Раздел 6.6.3. Функции Эйри», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Валле, Оливье; Соарес, Мануэль (2004), Функции Эйри и приложения к физике, Лондон: Imperial College Press, ISBN 978-1-86094-478-9, MR 2114198, заархивировано из оригинала 13 января 2010 г., извлечено 14 мая 2010 г.
Внешние ссылки
- , Энциклопедия математики, EMS Press, 2001 [1994]
- Вайсштейн, Эрик У. «Функции Эйри». MathWorld.
- Страницы функций Wolfram для функций Ai и Bi. Включает формулы, средство оценки функций и калькулятор построения графиков.
- Олвер, Ф. В. Дж. (2010), «Эйри и связанные функции», в Олвер, Фрэнк У. Дж. ; Lozier, Daniel M.; Бойсверт, Рональд Ф.; Кларк, Чарльз У. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248

 График Ai (x) красным цветом и Bi (x) синим
График Ai (x) красным цветом и Bi (x) синим 






![{\ displaystyle \ operatorname {Bi} (x) = {\ frac {1} {\ pi}} \ int _ {0 } ^ {\ infty} \ left [\ exp \ left (- {\ tfrac {t ^ {3}} {3}} + xt \ right) + \ sin \ left ({\ tfrac {t ^ {3}}) {3}} + xt \ right) \, \ right] dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3bcd1d018bad9c90fe2a8575dbb9038f2371ad4)


 Ai (синий) и синусоидальная / экспоненциальная асимптотика Ai (пурпурный)
Ai (синий) и синусоидальная / экспоненциальная асимптотика Ai (пурпурный)  Bi (синий) и синусоидальная / экспоненциальная асимптотика Bi (пурпурный)
Bi (синий) и синусоидальная / экспоненциальная асимптотика Bi (пурпурный) ![{\ displaystyle \ operatorname {Ai} (z) \ sim {\ dfrac {e ^ {- {\ frac {2} {3} } z ^ {\ frac {3} {2}}}} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0 } ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (n + {\ frac {5} {6}}) \ Gamma (n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {n}} {2 \ pi n! z ^ {3n / 2}}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e89d2a50ade6755bc8c233375d7c8fee8ea4516)
![{\ displaystyle \ operatorname {Bi} (z) \ sim {\ frac {e ^ {{\ frac {2} {3}} z ^ { \ frac {3} {2}}}} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {\ Gamma (n + {\ frac {5} {6}}) \ Gamma (n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {n}} {2 \ pi n! Z ^ {3n / 2}}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c08bd4d24ec332406e1c1a96d83002b8e3be44ac)
![{\ displaystyle {\ begin {align} \ operatorname {Ai} (-z) \ sim {} {\ frac {\ sin \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4 }} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {( -1) ^ {n} \ Gamma (2n + {\ frac {5} {6}}) \ Gamma (2n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n}} {2 \ pi (2n)! z ^ {3n}}} \ right] \\ [6pt] {} - {\ frac {\ cos \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4}} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1 } {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (2n + {\ frac {11} {6}}) \ Gamma (2n + {\ frac {7} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n + 1}} {2 \ pi (2n + 1)! Z ^ {3n + 3/2}}} \ right] \\ [6pt] \ operatorname {Bi} (-z) \ sim {} {\ frac {\ cos \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4}} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4} }}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (2n + {\ frac {5} {6}}) \ Gamma (2n + {\ frac {1} {6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n}} {2 \ pi (2n)! z ^ {3n}}} \ right] \\ [6pt] {} + {\ frac {\ sin \ left ({\ frac {2} {3}} z ^ {\ frac {3} {2}} + {\ frac {\ pi} {4 }} \ right)} {{\ sqrt {\ pi}} \, z ^ {\ frac {1} {4}}}} \ left [\ sum _ {n = 0} ^ {\ infty} {\ dfrac {(-1) ^ {n} \ Gamma (2n + {\ frac {11} {6}}) \ Gamma (2n + {\ frac {7} { 6}}) \ left ({\ frac {3} {4}} \ right) ^ {2n + 1}} {2 \ pi (2n + 1)! Z ^ {3n + 3/2}}} \ right ]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a8b6907a3908d270c8d98fa305880b40caee7b)

![{\ displaystyle \ Re \ left [\ operatorname {Ai} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92d14f4ea89c98289bdd7724aa97a65bc37be26c)
![{\ displaystyle \ Im \ left [\ operatorname {Ai} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f188455d8f10f38330bed9927837e68fdbc9df46)

![{\ displaystyle \ operatorname {arg } \ left [\ operatorname {Ai} (x + iy) \ right] \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2722a1be5b008fee5231676bfbecc9a6a15f6da)








![{\ displaystyle \ Re \ left [\ operatorname {Bi} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2dd29c05abcff762111d663f165d7c1055d3de)
![{\ displaystyle \ Im \ left [\ operatorname {Bi} (x + iy) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/456ed57b8b06b7da31229c0cb6989b24c2d9b3d8)

![{\ displaystyle \ operatorname {arg} \ left [\ operatorname {Bi} (x + iy) \ right] \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef422f3f85b66c485cf5b87ffa8b57b1b3e254a1)















 «функция Эйри» в смысле пропускания интерферометра Фабри-Перо
«функция Эйри» в смысле пропускания интерферометра Фабри-Перо 

 «Функция Эйри» в смысле дифракции на круглой апертуре.
«Функция Эйри» в смысле дифракции на круглой апертуре.