Гетеропереход

редактировать

A гетеропереход - это интерфейс, который возникает между двумя слоями или областями разнородных полупроводников. Эти полупроводниковые материалы имеют неравные запрещенные зоны в отличие от гомоперехода. Часто бывает выгодно создавать электронные энергетические диапазоны во многих приложениях твердотельных устройств, включая полупроводниковые лазеры, солнечные элементы и транзисторы. Комбинация нескольких гетеропереходов в устройстве называется гетероструктурой, хотя эти два термина обычно используются как взаимозаменяемые. Требование, чтобы каждый материал был полупроводником с неравной шириной запрещенной зоны, является несколько слабым, особенно на малых масштабах длины, где электронные свойства зависят от пространственных свойств. Более современное определение гетероперехода - это граница раздела между любыми двумя твердотельными материалами, включая кристаллические и аморфные структуры металлических, изолирующих проводников на быстрых ионах и полупроводников.

В 2000 г. Нобелевская премия по физике была присуждена совместно Герберту Кремеру из Калифорнийского университета, Санта-Барбара, Калифорния, США и Жорес И. Алферов из Института Иоффе, Санкт-Петербург, Россия за «разработку полупроводниковых гетероструктур, используемых в высокоскоростной фотографии и оптоэлектронике ».

Содержание

1 Производство и применение
2 Выравнивание энергетических полос
3 Несоответствие эффективных масс
4 Гетеропереходы в наномасштабе
5 См. Также
6 Ссылки
7 Дополнительная литература

Производство и применение

Производство гетеропереходов обычно требует использования молекулярно-лучевой эпитаксии (MBE) или химического осаждения из паровой фазы (CVD) для точного контроля осаждения. толщину и создают четко подобранную по решетке резкую границу раздела. Недавно исследуемой альтернативой является механическое наложение слоистых материалов в гетероструктуры Ван-дер-Ваальса.

Несмотря на свою дороговизну, гетеропереходы нашли применение во множестве специализированных приложений, где их уникальные характеристики имеют решающее значение:

Солнечные элементы: Гетеропереходы обычно образуются через поверхность раздела кристаллической кремниевой подложки и пассивирующего слоя аморфного кремния в солнечных элементах. Гетеропереход со структурой солнечных элементов с внутренним тонким слоем (HIT) был впервые разработан в 1983 году и коммерциализирован компанией Sanyo / Panasonic. В настоящее время солнечные элементы HIT являются рекордсменами по эффективности однопереходных кремниевых солнечных элементов с эффективностью преобразования 26,7%.
Лазеры: использование гетеропереходов в лазерах было впервые предложено в 1963 году, когда Герберт Кремер, выдающийся ученый в этой области, предположил, что инверсия населенности может быть значительно усилена гетероструктурами. За счет включения материала с прямой запрещенной зоной меньшего размера, такого как GaAs, между двумя более крупными запрещенными слоями, такими как AlAs, носители могут быть ограничены так, чтобы генерация может возникать при комнатной температуре с низкими пороговыми токами. Материаловедению потребовалось много лет, чтобы догнать идеи Кремера, но теперь это отраслевой стандарт. Позже было обнаружено, что шириной запрещенной зоны можно управлять, используя преимущества квантовых размерных эффектов в гетероструктурах с квантовыми ямами. Кроме того, гетероструктуры могут использоваться в качестве волноводов с индексом шага, который возникает на границе раздела, что является еще одним важным преимуществом их использования в полупроводниковых лазерах. Полупроводниковые диодные лазеры, используемые в CD и DVD проигрывателях, и волоконно-оптических приемопередатчиках изготавливаются с использованием чередующихся слоев различных III-V и II-VI составные полупроводники для формирования лазерных гетероструктур.
Биполярные транзисторы: когда гетеропереход используется в качестве основы - эмиттерный переход транзистора с биполярным переходом, чрезвычайно высокое прямое усиление и низкое обратное усиление. Это обеспечивает очень хорошую работу на высоких частотах (значения от десятков до сотен ГГц) и низкие токи утечки. Это устройство называется биполярным транзистором с гетеропереходом (HBT).
Полевые транзисторы: Гетеропереходы используются в транзисторах с высокой подвижностью электронов (HEMT), которые могут работать со значительными более высокие частоты (более 500 ГГц). Правильный профиль легирования и выравнивание полос приводят к чрезвычайно высокой подвижности электронов за счет создания двумерного электронного газа в пределах свободной от примеси области где может происходить очень небольшое рассеяние.

Выравнивание энергетических зон

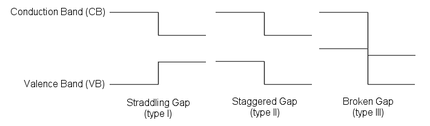
Три типа полупроводниковых гетеропереходов, организованных путем выравнивания зон.

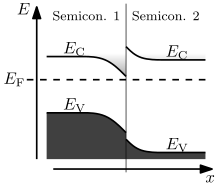Зонная диаграмма для встречной щели, n-n полупроводниковый гетеропереход в равновесии.

Поведение полупроводникового перехода в решающей степени зависит от выравнивания энергетических зон на границе раздела. Полупроводниковые интерфейсы можно разделить на три типа гетеропереходов: встречный зазор (тип I), ступенчатый зазор (тип II) или разорванный зазор (тип III), как показано на рисунке. Вдали от стыка изгиб полосы может быть вычислен на основе обычной процедуры решения уравнения Пуассона.

. Существуют различные модели для прогнозирования выравнивания полосы.

Простейшей (и наименее точной) моделью является правило Андерсона, которое предсказывает выравнивание полос на основе свойств границ раздела вакуум-полупроводник (в частности, сродства вакуума к электрону ). Основным ограничением является пренебрежение химической связью.
Было предложено общее правило анионов, которое предполагает, что, поскольку валентная зона связана с анионными состояниями, материалы с одинаковыми анионами должны иметь очень малые смещения валентных зон. Однако это не объясняет данные, а связано с тенденцией к тому, что два материала с разными анионами имеют тенденцию иметь большие смещения валентной зоны, чем смещения зоны проводимости.
Tersoff предложила модель щелевого состояния, основанную на более знакомом переходах металл-полупроводник, где смещение зоны проводимости задается разницей в высоте барьера Шоттки. Эта модель включает дипольный слой на границе раздела между двумя полупроводниками, который возникает в результате туннелирования электронов из зоны проводимости одного материала в зазор другого (аналог металла -индуцированные состояния разрыва ). Эта модель хорошо согласуется с системами, в которых оба материала близко согласованы по решетке, например GaAs / AlGaAs.
Правило 60:40 является эвристическим для конкретного случая переходов между полупроводником GaAs и полупроводниковый сплав Al xGa1-x As. Поскольку x в Al xGa1 − x При изменении стороны от 0 до 1, отношение $Δ EC / Δ EV {\ displaystyle \ Delta E_ {C} / \ Delta E_ {V} }$ $\ Delta E_C / \ Delta E_V$ стремится поддерживать значение 60/40. Для сравнения, правило Андерсона предсказывает $Δ EC / Δ EV = 0,73 / 0,27 {\ displaystyle \ Delta E_ {C} / \ Delta E_ {V} = 0,73 / 0,27}$ $\ Delta E_C / \ Delta E_V = 0,73 / 0,27$ для GaAs / AlAs перехода (x = 1).

Типичный метод измерения смещений полос - вычисление их по измерению энергии экситонов в спектре люминесценции .

Эффективная масса несоответствие

Когда гетеропереход образован двумя разными полупроводниками, может быть изготовлена квантовая яма из-за различия в зонной структуре. Чтобы вычислить статические уровни энергии в пределах достигнутой квантовой ямы, становится важным понимание изменения или несоответствия эффективной массы на гетеропереходе. Квантовая яма, определенная в гетеропереходе, может рассматриваться как потенциал с конечной ямой с шириной $l w {\ displaystyle l_ {w}}$ $l_w$ . Кроме того, в 1966 г. Conley et al. и Бен-Дэниел и Дюк сообщили о граничном условии для огибающей функции в квантовой яме, известном как граничное условие Бен-Дэниела-Дьюка. Согласно им, огибающая функция в изготовленной квантовой яме должна удовлетворять граничному условию, которое гласит, что $ψ (z) {\ displaystyle \ psi (z)}$ ${\ displaystyle \ psi (z)}$ и $1 m ∗ ∂ ∂ Z ψ (z) {\ displaystyle {\ frac {1} {m ^ {*}}} {\ partial \ over {\ partial z}} \ psi (z) \,}$ ${\ displaystyle {\ frac {1} {m ^ {*}}} {\ partial \ over {\ partial z}} \ psi (z) \,}$ оба непрерывно в интерфейсных областях.

Математические детали разработаны для примера квантовой ямы.

Использование уравнения Шредингера для конечной ямы шириной $lw {\ displaystyle l_ {w}}$ $l_w$ с центром в 0, уравнение для полученной квантовой ямы можно записать как:

- ℏ 2 2 mb ∗ d 2 ψ (z) dz 2 + V ψ (z) = E ψ ( z) для z < − l w 2 ( 1) {\displaystyle -{\frac {\hbar ^{2}}{2m_{b}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}+V\psi (z)=E\psi (z)\quad \quad {\text{ for }}z<-{\frac {l_{w}}{2}}\quad \quad (1)}

- \ frac {\ hbar ^ 2} {2m_b ^ *} \ frac {\ mathrm {d} ^ 2 \ psi (z)} {\ mathrm {d} z ^ 2} + V \ psi ( z) = E \ psi (z) \ quad \ quad \ text {for} z <- \ frac {l_w} {2} \ quad \ quad (1)

- ℏ 2 2 mw ∗ d 2 ψ (z) dz 2 = E ψ (z) для - lw 2 < z < + l w 2 ( 2) {\displaystyle \quad \quad -{\frac {\hbar ^{2}}{2m_{w}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}=E\psi (z)\quad \quad {\text{ for }}-{\frac {l_{w}}{2}}

\ quad \ quad - \ frac {\ hbar ^ 2} {2m_w ^ *} \ frac {\ mathrm {d} ^ 2 \ psi ( z)} {\ mathrm {d} z ^ 2} = E \ psi (z) \ quad \ quad \ text {for} - \ frac {l_w} {2} <z <+ \ frac {l_w} {2} \ quad \ quad (2)

- ℏ 2 2 mb ∗ d 2 ψ (z) dz 2 + V ψ (z) знак равно E ψ (z) для z>+ lw 2 (3) {\ displaystyle - {\ frac {\ hbar ^ {2}} {2m_ {b} ^ {*}}} {\ frac {\ mathrm {d} ^ {2} \ psi (z)} {\ mathrm {d} z ^ {2}}} + V \ psi (z) = E \ psi (z) \ quad {\ text {for}} z>+ {\ frac {l_ {w}} {2}} \ quad \ quad (3)}

-\frac{\hbar^2}{2m_b^*} \frac{\mathrm{d}^2 \psi(z)}{\mathrm{d}z^2} + V \psi(z) = E \psi(z) \quad \text{ for } z>+ \ frac {l_w} {2} \ quad \ quad (3)

Решение для приведенных выше уравнений хорошо известно, только с разными (модифицированными) k и $κ {\ displaystyle \ kappa}$ $\ каппа$

k = 2 mw E ℏ κ = 2 mb (V - E) ℏ ( 4) {\ displaystyle к = {\ гидроразрыва {\ sqrt {2m_ {w} E}} {\ hbar}} \ quad \ quad \ kappa = {\ frac {\ sqrt {2m_ {b} (VE)}} { \ hbar}} \ quad \ quad (4)}

k = \ frac {\ sqrt {2 m_w E}} { \ hbar} \ quad \ quad \ kappa = \ frac {\ sqrt {2 m_b (V- E)}} {\ hbar} \ quad \ quad (4)

В точке z = $+ lw 2 {\ displaystyle + {\ frac {l_ {w}} {2}}}$ $+ \ frac {l_w} {2}$ даже -чистое решение может быть получено из

A cos ⁡ (klw 2) = B exp ⁡ (- κ lw 2) (5) {\ displaystyle A \ cos ({\ frac {kl_ {w}} {2}}) = B \ exp (- {\ frac {\ kappa l_ {w}} {2}}) \ quad \ quad (5)}

A \ cos (\ frac {k l_w} {2}) = B \ exp (- \ frac {\ kappa l_w} {2}) \ quad \ quad (5)

Взяв производную от (5) и умножив обе части на $1 m ∗ {\ displaystyle {\ frac {1} {m ^ {*}}}}$ $\ frac {1} {m ^ *}$

- k A mw ∗ sin ⁡ (klw 2) = - κ B mb ∗ exp ⁡ (- κ lw 2) (6) {\ displaystyle - {\ frac {kA} {m_ {w} ^ {*}}} \ sin ({\ frac {kl_ {w}} {2}}) = - {\ frac {\ kappa B} { m_ {b} ^ {*}}} \ exp (- {\ frac {\ kappa l_ {w}} {2}}) \ quad \ quad (6)}

- \ frac {kA} {m_w ^ *} \ sin (\ frac {k l_w} {2}) = - \ frac { \ kappa B} {m_b ^ *} \ exp (- \ frac {\ kappa l_w} {2}) \ quad \ quad (6)

Разделив (6) на (5), Функция решения с четностью может быть получена,

f (E) = - kmw ∗ tan ⁡ (klw 2) - κ mb ∗ = 0 (7) {\ displaystyle f (E) = - {\ frac {k} {m_ {w} ^ {*}}} \ tan ({\ frac {kl_ {w}} {2}}) - {\ frac {\ kappa} {m_ {b} ^ {*}}} = 0 \ quad \ quad (7)}

f (E) = - \ frac {k} {m_w ^ *} \ tan (\ frac {k l_w} {2}) - \ frac {\ kappa} {m_b ^ *} = 0 \ quad \ quad (7)

Аналогично для нечетной четности s olution,

е (E) = - kmw * кроватка ⁡ (klw 2) + κ mb * = 0 (8) {\ displaystyle f (E) = - {\ frac {k} {m_ {w} ^ { *}}} \ cot ({\ frac {kl_ {w}} {2}}) + {\ frac {\ kappa} {m_ {b} ^ {*}}} = 0 \ quad \ quad (8)}

f (E) = - \ frac {k} {m_w ^ *} \ cot (\ frac {k l_w} {2}) + \ frac {\ kappa} {m_b ^ *} = 0 \ quad \ quad (8)

Для численного решения взятие производных от (7) и (8) дает

четность:

dfd E = 1 mw ∗ dkd E tan ⁡ (klw 2) + kmw ∗ сек 2 ⁡ (klw 2) × lw 2 dkd E - 1 mb ∗ d κ d E (9-1) {\ displaystyle {\ frac {df} {dE}} = {\ frac {1} {m_ {w} ^ {*}}} {\ frac {dk} {dE}} \ tan ({\ frac {kl_ {w}} {2}}) + {\ frac {k} {m_ {w} ^ { *}}} \ sec ^ {2} ({\ frac {kl_ {w}} {2}}) \ times {\ frac {l_ {w}} {2}} {\ frac {dk} {dE}} - {\ frac {1} {m_ {b} ^ {*}}} {\ frac {d \ kappa} {dE}} \ quad \ quad (9-1)}

\ frac {df} {dE} = \ frac {1} {m_w ^ *} \ frac {dk} {dE} \ tan (\ frac {k l_w} { 2}) + \ frac {k} {m_w ^ *} \ sec ^ 2 (\ frac {k l_w} {2}) \ times \ frac {l_w} {2} \ frac {dk} {dE} - \ frac {1} {m_b ^ *} \ frac {d \ kappa} {dE} \ quad \ quad (9-1)

нечетная четность:

dfd E = 1 mw ∗ dkd E детская кроватка ⁡ (klw 2) - kmw ∗ csc 2 ⁡ (klw 2) × lw 2 dkd E + 1 mb ∗ d κ d E (9 - 2) {\ displaystyle {\ frac {df} {dE}} = {\ frac {1} {m_ {w} ^ {*}}} {\ frac {dk} {dE}} \ cot ({\ frac {kl_ {w}} {2}}) - {\ frac {k} {m_ {w} ^ {*}}} \ csc ^ {2} ({\ frac {kl_ {w}} {2}}) \ times {\ frac {l_ {w}} { 2}} {\ frac {dk} {dE}} + {\ fra c {1} {m_ {b} ^ {*}}} {\ frac {d \ kappa} {dE}} \ quad \ quad (9-2)}

\ frac {df} {dE} = \ frac {1} {m_w ^ *} \ frac {dk} {dE} \ cot ( \ frac {k l_w} {2}) - \ frac {k} {m_w ^ *} \ csc ^ 2 (\ frac {k l_w} {2}) \ times \ frac {l_w} {2} \ frac {dk} {dE} + \ frac {1} {m_b ^ *} \ frac {d \ kappa} {dE} \ quad \ quad (9-2)

где $dkd E = 2 mw ∗ 2 E ℏ d κ d E = - 2 mb ∗ 2 V - E ℏ {\ displaystyle {\ frac {dk} {dE}} = {\ frac {\ sqrt {2m_ {w} ^ {*}}} {2 {\ sqrt {E}} \ hbar}} \ quad \ quad \ quad {\ frac {d \ kappa} {dE}} = - {\ frac {\ sqrt {2m_ {b} ^ {*}}} {2 {\ sqrt {VE}} \ hbar}}}$ $\ frac {dk} {dE} = \ frac {\ sqrt {2 m_w ^ *}} {2 \ sqrt E \ hbar} \ quad \ quad \ quad \ frac {d \ kappa} {dE} = - \ frac {\ sqrt {2 m_b ^ *}} {2 \ sqrt {VE} \ hbar}$ .

Разница в эффективных массах материалов приводит к большей разнице в энергиях основного состояния.

Наноразмерные гетеропереходы

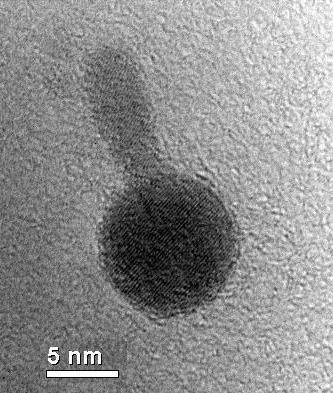
Изображение наноразмерного гетероперехода между оксидом железа (Fe 3O4- сфера) и сульфидом кадмия (CdS - стержень), полученное с помощью TEM. Этот смещенный переход со ступенчатой щелью (тип II) был синтезирован Хантером МакДэниелом и доктором Мунсаб Шимом в Университете Иллинойса в Урбане-Шампейне в 2007 году.

В квантовых точках энергии зон зависят от кристалла. размер из-за квантовых размерных эффектов . Это позволяет проектировать смещение полосы в наноразмерных гетероструктурах. Можно использовать те же материалы, но изменить тип соединения, скажем, с двухстороннего (тип I) на ступенчатый (тип II), путем изменения размера или толщины задействованных кристаллов. Наиболее распространенная система с наноразмерной гетероструктурой - это ZnS на CdSe (CdSe @ ZnS), имеющая смещение поперечного зазора (тип I). В этой системе гораздо большая запрещенная зона ZnS пассивирует поверхность флуоресцентного ядра CdSe, тем самым увеличивая квантовую эффективность люминесценция. Существует дополнительный бонус в виде повышенной термостабильности благодаря более прочным связям в оболочке из ZnS, о чем свидетельствует большая ширина запрещенной зоны. Поскольку и CdSe, и ZnS растут в кристаллической фазе цинковой обманки и имеют близкую решетку, предпочтительным является рост ядра-оболочки. В других системах или при других условиях выращивания можно вырастить анизотропные структуры, подобные той, что видна на изображении справа.

Было показано, что движущей силой для переноса заряда между зонами проводимости в этих структурах является смещение зоны проводимости. Уменьшая размер нанокристаллов CdSe , выращенных на TiO 2, Robel et al. обнаружили, что электроны быстрее переходят из более высокой зоны проводимости CdSe в TiO 2. В CdSe квантовый размерный эффект гораздо более выражен в зоне проводимости из-за меньшей эффективной массы, чем в валентной зоне, и это имеет место в большинстве полупроводников. Следовательно, проектирование смещения зоны проводимости обычно намного проще с помощью наноразмерных гетеропереходов. Для шахматных (тип II) смещенных наноразмерных гетеропереходов может происходить фотоиндуцированное разделение зарядов, поскольку там самое низкое энергетическое состояние для дырок может быть на одной стороне перехода, тогда как самая низкая энергия для электронов с противоположной стороны. Было высказано предположение, что для фотокатализа, особенно для расщепления воды с помощью солнечной энергии, можно использовать наноразмерные гетеропереходы с анизотропной шахматной щелью (тип II).

См. Также

Гомопереход, p – n переход - переход, включающий два типа одного и того же полупроводника.
Переход металл – полупроводник - переход металла на полупроводник.