Интерферометр Фабри - Перо

редактировать

Интерференционные полосы, показывающие тонкую структуру, из эталона Фабри - Перо. В качестве источника используется охлаждающая дейтериевая лампа .

В оптике, интерферометр Фабри - Перо (FPI ) или эталон представляет собой оптический резонатор , сделанный из двух параллельных отражающих поверхностей (то есть: тонких зеркал ). Оптические волны могут проходить через оптический резонатор, только когда они находятся в резонансе с ним. Он назван в честь Шарля Фабри и Альфреда Перо, которые разработали прибор в 1899 году. Эталон происходит от французского эталон, что означает «измерительный прибор» или «эталон».

Эталоны широко используются в телекоммуникациях, лазерах и спектроскопии для управления и измерения длин волн света. Последние достижения в технологии изготовления позволяют создавать очень точные перестраиваемые интерферометры Фабри - Перо. Устройство называется интерферометром, когда расстояние между двумя поверхностями (вместе с ним и длиной резонанса) может быть изменено, и эталоном, когда расстояние фиксировано (однако эти два часто используются как взаимозаменяемые)..

Содержание

1 Базовое описание
2 Приложения
3 Теория
- 3.1 Потери в резонаторе, выходящий свет, резонансные частоты и формы спектральных линий
- 3.2 Общее распределение Эйри: коэффициент усиления внутреннего резонанса
- 3.3 Другие распределения Эйри
- 3.4 Распределение Эйри как сумма профилей мод
- 3.5 Характеристика резонатора Фабри-Перо: лоренцевская ширина линии и точность
- 3.6 Сканирование резонатора Фабри-Перо: ширина линии Эйри и изящество
- 3.7 Частотно-зависимые коэффициенты отражения зеркал
- 3.8 Резонатор Фабри-Перо с собственными оптическими потерями
- 3.9 Описание резонатора Фабри-Перо в пространстве длин волн
4 См. Также
5 Примечания
6 Ссылки
7 Внешние ссылки

Основное описание

Интерферометр Фабри - Перо, использующий пару частично отражающих, слегка заклиненных оптических плоскостей. На этом рисунке угол клина сильно преувеличен; на самом деле необходима лишь доля градуса, чтобы избежать призрачных полос. Низкое качество изображения по сравнению с высоким качеством изображения соответствует коэффициентам отражения зеркала 4% (голое стекло) и 95%.

Сердцем интерферометра Фабри-Перо является пара частично отражающих стеклянных оптических плоскостей, расположенных на расстоянии друг от друга. Расстояние от микрометров до сантиметров, при этом отражающие поверхности обращены друг к другу. (В качестве альтернативы эталон Фабри - Перо использует одну пластину с двумя параллельными отражающими поверхностями.) Плоскости в интерферометре часто имеют клиновидную, чтобы задние поверхности не создавались интерференционными полосами; задние часто также имеют антибликовое покрытие .

В типичной системе освещения обеспечивается диффузным датчиком, установленным в фокальной поверхности коллимирующей линзы . Фокусирующая линза после пары плоских поверхностей создала бы перевернутое изображение источника, если бы плоские поверхности отсутствовали; весь свет, излучаемый из точки на выходнике, фокусируется в единственной точке плоскости изображения системы. На прилагаемой иллюстрации прослеживается только один луч, испускаемый из точки A источника. Когда луч проходит через спаренные плоскости, он многократно отражается, создавая несколько прошедших лучей, которые собираются фокусирующей линзой и переносятся в точку A 'на экране. Полная картина интерференции имеет вид набора концентрических колец. Острота колец зависит от отражающей способности плоских поверхностей. Если коэффициент отражения высокий, что приводит к высокой добротности , монохроматический свет набор узких ярких колец на темном фоне. Считается, что интерферометр Фабри - Перо с высокой добротностью обладает высокой точностью.

Приложения

Коммерческое устройство Фабри-Перо

Телекоммуникационные сети, использующие мультиплексирование с разделением по длине волны 400>, имеют мультиплексоры ввода-вывода с банками миниатюрных настроек плавленый кварц или алмаз эталоны. Это небольшие переливающиеся кубики стороной около 2 мм, закрепленные на небольших высокоточных стойках. Материалы выбраны таким образом, чтобы поддерживать стабильное расстояние от зеркала до зеркала и поддерживать стабильные частоты при изменении температуры. Он обладает увеличенной теплопроводностью. В 2005 году некоторые производители телекоммуникационного оборудования начали использовать твердые эталоны, которые сами по себе являются оптическими волокнами. Это устраняет большинство трудностей, связанных с установкой, выравниванием и охлаждением.
Дихроичные фильтры изготавливаются путем нанесения серии эталонных слоев на оптическую поверхность посредством осаждения из паровой фазы. Эти оптические фильтры обычно имеют более точные полосы отражения и пропускания, чемающие поглощающие фильтры. При правильной конструкции они работают холоднее, чем поглощающие фильтры, потому что могут отражать вредную длину волны. Дихроичные фильтры широко используются в оптическом оборудовании, таком как источники света, камеры, астрономическое оборудование и лазерные системы.
Оптические волномеры и некоторые анализаторы оптического фактора используют Fabry– Интерферометры Перо с различными свободными спектральными диапазонами для определения длины волны света с большой точностью.
Лазерные резонаторы часто называют одного резонатора Фабри - Перо, хотя для многих типов лазеров коэффициент отражения зеркала близка к 100%, что делает его более похожим на интерферометр Жира - Турнуа. В полупроводниковых диодных лазерах иногда используется истинная геометрия. Фабри - Перо из за сложности покрытия торцевых поверхностей кристалла. Квантовые каскадные лазеры часто используют резонаторы Фабри-Перо для поддержания генерации без необходимости в каких-либо покрытиях граней из-за высокого усиления.
Эталоны часто помещаются внутри лазерного резонатора. при создании одномодовых лазеров. Без эталона лазер обычно будет излучать свет в диапазоне длин волн, соответствующем ряду мод >, которые аналогичны модам Фабри - Перо. Вставка эталона в резонатор лазера может подавить все моды резонатора, кроме одной, тем изменяя работу лазера лазера с многомодового на одномодовый.
Эталоны Фабри - Перо могут увеличить длину в лазерной абсорбционной спектрометрии, в частности в методх кольцевого опускания резонанса.
Эталон Фабри-Перо может быть использован для создания спектрометра , способного наблюдать эффект Зеемана, где спектральные линии расположены слишком близко друг к другу, чтобы их можно было отличить от нормального спектрометр.
В астрономии эталон используется для выбора изображения одного для построения изображения. Наиболее распространенной является строка H-alpha строки солнце. Линия Ca-K от Солнца также обычно отображается с использованием эталонов.
Датчик метана для Марса (MSM) на индийском Мангальяна является примером Фабри-Перо. Это был первый космический инструмент Фабри Перо на момент запуска Мангальяна. Он показал не отличное излучение, поглощенное метаном, поглощенное углекислым газом и другими газами, позже его назвали картографом альбедо.
При обнаружении гравитационных волн полость используется для хранения фотонов в течение почти миллисекунды, пока они отражаются вверх и вниз между зеркалами. Это увеличивает время, в течение которого гравитационная волна может взаимодействовать со светом, что приводит к лучшей чувствительности на низких частотах. Этот принцип используется в таких детекторах, как LIGO и Virgo, которые состоят из интерферометра Майкельсона с резонатором Фабри - Перо длиной в несколько километров в оба оружия. Меньшие резонаторы, обычно называемые очистителями мод, используются для пространственной фильтрации и стабилизации частоты основного лазера.

Теория

Потери в резонаторе, выходящий свет, резонансные частоты и формы спектральных линий

Спектральный отклик резонатора Фабри-Перо основан на интерференции между светом, направленным в него, и светом, циркулирующий в резонаторе. Конструктивная интерференция возникает, если два луча находятся в фазе , что приводит к резонансному усилению света внутри резонатора. Если два луча не совпадают, внутри резонатора сохраняется лишь небольшая часть выпущенного света. Сохраненный, прошедший и отраженный свет спектрально модифицируется по сравнению с падающим светом.

Предположим, что двухзеркальный резонатор Фабри-Перо геометрической длины $ℓ {\ displaystyle \ ell}$ $\ ell$ , однородно заполненный средой с показателем преломления $n {\ displaystyle n}$ $n$ . Свет попадает в резонатор при нормальном падении. Время прохождения света $t RT {\ displaystyle t _ {\ rm {RT}}}$ ${\ displaystyle t _ {\ rm {RT}}}$ в резонаторе со скоростью $c = c 0 / n {\ displaystyle c = c_ {0} / n}$ ${\ displaystyle c = c_ {0} / n}$ , где $c 0 {\ displaystyle c_ {0}}$ $c_ {0}$ - скорость света в вакууме, а свободный спектральный диапазон $Δ ν FSR {\ displaystyle \ Delta \ nu _ {\ rm {FSR}}}$ ${\ displaystyle \ Delta \ nu _ {\ rm {FSR} }}$ даются как

t RT = 1 Δ ν FSR = 2 ℓ c. {\ displaystyle t _ {\ rm {RT}} = {\ frac {1} {\ Delta \ nu _ {\ rm {FSR}}}} = {\ frac {2 \ ell} {c}}.}

{\ displaystyle t _ {\ rm {RT}} = {\ frac {1} {\ Delta \ nu _ {\ rm {FSR}}}} = {\ frac {2 \ ell} {c}}.}

Коэффициенты отражения электрического поля и интенсивности $ri {\ displaystyle r_ {i}}$ $r_ {i}$ и $R i {\ displaystyle R_ {i}}$ $R_ {i}$ , соответственно, при зеркало $i {\ displaystyle i}$ $я$ are

| г я | 2 = R i. {\ displaystyle | r_ {i} | ^ {2} = R_ {i}.}

{\ displaystyle | r_ {i} | ^ {2} = R_ {я}.}

Если нет других потерь в резонаторе, затухание света за круговой обход количественно определяет константную скорость затухания выходного сигнала $1 / τ выход, {\ displaystyle 1 / \ tau _ { \ rm {out}},}$ ${\ displaystyle 1 / \ tau _ {\ rm {out}},}$

R 1 R 2 = e - t RT / τ выход, {\ displaystyle R_ {1} R_ {2} = e ^ {- t _ {\ rm {RT}} / \ tau _ {\ rm {out}}},}

{\ displaystyle R_ {1} R_ {2} = e ^ {- t _ {\ rm { RT}} / \ tau _ {\ rm {out}}},}

и время распада фотона $τ c {\ displaystyle \ tau _ {c}}$ $\ tau_c$ резонатора тогда определяется как

1 τ c = 1 τ out = - ln ⁡ (R 1 R 2) t RT. {\ displaystyle {\ frac {1} {\ tau _ {c}}} = {\ frac {1} {\ tau _ {\ rm {out}}}} = {\ frac {- \ ln {(R_ { 1} R_ {2})}} {t _ {\ rm {RT}}}}.}

{\ displaystyle {\ frac {1} {\ tau _ {c}}} = {\ frac {1} {\ tau _ {\ rm {out}}}} = {\ frac {- \ ln {(R_ {1}) R_ {2})}} {t_ {\ rm {RT}}}}.}

С $ϕ (ν) {\ displaystyle \ phi (\ nu)}$ ${\ displaystyle \ phi (\ nu)}$ количественная оценка однопроходный фазовый сдвиг, который свет проявляет при распространении от одного зеркала к другому, фазовый сдвиг в оба конца на частоте $ν {\ displaystyle \ nu}$ $\ nu$ накапливается до

2 ϕ (ν) = 2 π ν t RT. {\ displaystyle 2 \ phi (\ nu) = 2 \ pi \ nu t _ {\ rm {RT}}.}

{\ displaysty ле 2 \ фи (\ ню) = 2 \ пи \ ню т _ {\ rm {RT}}.}

Резонансы на частотах, на которые светет проявляет конструктивную интерференцию после одного пути и туда обратно. Каждый режим резонатора с его индексом режима $q {\ displaystyle q}$ $q$ , где $q {\ displaystyle q}$ $q$ - целое число в интервале [ $- ∞ {\ displaystyle - \ infty}$ ${\ displaystyle - \ infty}$ ,..., −1, 0, 1,..., $∞ {\ displaystyle \ infty}$ $\ infty$ ], является новой с резонансной частоты $ν q {\ displaystyle \ nu _ {q}}$ ${\ displaystyle \ nu _ {q}}$ и волновым числом $kq {\ displaystyle k_ {q}}$ ${\ displaystyle k_ {q}}$ ,

ν q = q Δ ν FSR ⇒ kq = 2 π q Δ ν FSR c. {\ displaystyle \ nu _ {q} = q \ Delta \ nu _ {\ rm {FSR}} \ Rightarrow k_ {q} = {\ frac {2 \ pi q \ Delta \ nu _ {\ rm {FSR}} } {c}}.}

{\ displaystyle \ nu _ {q} = q \ Delta \ nu _ {\ rm {FSR}} \ Rightarrow k_ {q} = {\ frac {2 \ pi q \ Delta \ nu _ {\ rm {FSR}}} {c}}.}

Два режима с противоположными значениями $± q {\ displaystyle \ pm q}$ ${\ displaystyle \ pm q}$ и $± k {\ displaystyle \ pm k}$ ${\ displaystyle \ pm k}$ модального индекса и волнового числа, соответственно, физически представляющие противоположные направления распространения, имеют одно и то же абсолютное значение $| ν q | {\ displaystyle \ left | \ nu _ {q} \ right |}$ ${\ displaystyle \ left | \ nu _ {q} \ right |}$ частоты.

Затухающее электрическое поле с окружением $ν q {\ displaystyle \ nu _ {q}}$ ${\ displaystyle \ nu _ {q}}$ представлен затухающим гармоническим колебанием с начальной амплитудой $E q, s {\ displaystyle E_ {q, s}}$ ${\ displaystyle E_ {q, s}}$ и постоянной времени затухания $2 τ c {\ displaystyle 2 \ tau _ {c}}$ ${\ displaystyle 2 \ tau _ {c}}$ . В векторной записи это может быть выражено как

E q (t) = E q, s e i 2 π ν q t e - t 2 τ c. {\ displaystyle E_ {q} (t) = E_ {q, s} e ^ {i2 \ pi \ nu _ {q} t} e ^ {- {\ frac {t} {2 \ tau _ {c}} }}.}

{\ стиль отображения E_ {q} (t) = E_ {q, s} e ^ {i2 \ pi \ nu _ {q} t} e ^ {- {\ frac {t} {2 \ tau _ {c}}}}.}

Преобразование Фурье электрического поля во времени дает электрическое поле на единицу частотного интервала,

E ~ q (ν) = ∫ - ∞ + ∞ E q (t) e - i 2 π ν tdt = E q, s 1 (2 τ c) - 1 + i 2 π (ν - ν q). {\ Displaystyle {\ тильда {E}} _ {q} (\ nu) = \ int _ {- \ infty} ^ {+ \ infty} E_ {q} (t) e ^ {- i2 \ pi \ nu t } \, dt = E_ {q, s} {\ frac {1} {(2 \ tau _ {c}) ^ {- 1} + i2 \ pi (\ nu - \ nu _ {q})}}. }

{\ Displaystyle {\ тильда {E}} _ {q} (\ nu) = \ int _ {- \ infty} ^ {+ \ infty} E_ {q} (t) e ^ {- i2 \ pi \ nu t } \, dt = E_ {q, s} {\ frac {1} {(2 \ tau _ {c}) ^ {- 1} + i2 \ pi (\ nu - \ nu _ {q})}}. }

Каждая мода имеет нормированную форму спектральной линии на единицу частотного интервала, заданную как

γ ~ q (ν) = 1 τ c | E ~ q (ν) E q, s | 2 знака равно 1 τ с 1 (2 τ с) - 2 + 4 π 2 (ν - ν q) 2, {\ displaystyle {\ tilde {\ gamma}} _ {q} (\ nu) = {\ frac { 1} {\ tau _ {c}}} \ left | {\ frac {{\ tilde {E}} _ {q} (\ nu)} {E_ {q, s}}} \ right | ^ {2} = {\ frac {1} {\ tau _ {c}}} {\ frac {1} {(2 \ tau _ {c}) ^ {- 2} +4 \ pi ^ {2} ( \ nu - \ nu _ {q}) ^ {2}}},}

{\ displaystyle {\ tilde {\ gamma}} _ {q} (\ nu) = {\ frac {1} {\ tau _ {c}} } \ left | {\ frac {{\ tilde {E}} _ {q} (\ nu)} {E_ {q, s}}} \ right | ^ {2} = {\ frac {1} {\ tau _ {c}}} {\ frac {1} {(2 \ tau _ {c}) ^ {- 2} +4 \ pi ^ {2} ( \ nu - \ nu _ {q}) ^ {2}}},}

, интеграл частоты которого равен единице. Вводя ширину линии при полной ширине полувысоте (FWHM) $Δ ν c {\ displaystyle \ Delta \ nu _ {c}}$ ${\ displaystyle \ Delta \ nu _ {c}}$ ${\ displaystyle \ Delta \ nu _ {c}}$ формы спектральной линии Лоренца, мы получаем

Δ ν c = 1 2 π τ c ⇒ γ ~ q (ν) = 1 π Δ ν c / 2 (Δ ν c / 2) 2 + (ν - ν q) 2 = 2 π Δ ν c (Δ ν в) 2 + 4 (ν - ν q) 2, {\ displaystyle \ Delta \ nu _ {c} = {\ frac {1} {2 \ pi \ tau _ {c}}} \ Rightarrow {\ tilde {\ гамма}} _ {q} (\ nu) = {\ frac {1} {\ pi}} {\ frac {\ Delta \ nu _ {c} / 2} {(\ Delta \ nu _ {c} / 2) ^ {2} + ( \ nu - \ nu _ {q}) ^ {2}}} = {\ frac {2} {\ pi}} {\ frac {\ Delta \ nu _ {c}} {(\ Delta \ nu _ {c }) ^ {2} +4 (\ nu - \ nu _ {q}) ^ {2}}},}

{\ displaystyle \ Delta \ nu _ {c} = {\ frac {1} {2 \ pi \ tau _ {c}} } \ Rightarrow {\ тильда {\ gamma}} _ {q} (\ nu) = {\ frac {1} {\ pi}} {\ frac {\ Delta \ nu _ {c} / 2} {(\ Delta \ nu _ {c} / 2) ^ {2} + (\ nu - \ nu _ {q}) ^ {2 }}} = {\ frac {2} {\ pi}} {\ frac {\ Delta \ nu _ {c}} {(\ Delta \ nu _ {c}) ^ {2} +4 (\ nu - \ ню _ {q}) ^ {2}}},}

выражается либо через половину ширины -максимальная (HWHM) ширина линии $Δ ν c / 2 {\ displaystyle \ Delta \ nu _ {c} / 2}$ ${\ displaystyle \ Delta \ nu _ {c} / 2}$ или ширина линии FWHM $Δ ν c {\ displaystyle \ Delta \ ню _ {c}}$ ${\ displaystyle \ Delta \ nu _ {c}}$ . После калибровки по высоте пика, равной единице, мы получаем лоренцев линии:

γ q, L (ν) = π 2 Δ ν c γ ~ q (ν) = (Δ ν c / 2) 2 (Δ ν c / 2) 2 + (ν - ν q) 2 знак равно (Δ ν с) 2 (Δ ν с) 2 + 4 (ν - ν q) 2. {\ displaystyle \ gamma _ {q, L} (\ nu) = {\ frac {\ pi} {2}} \ Delta \ nu _ {c} {\ tilde {\ gamma}} _ {q} (\ nu) = {\ frac {(\ Delta \ nu _ {c} / 2) ^ {2}} {(\ Delta \ nu _ {c} / 2) ^ {2} + (\ nu - \ nu _ {q}) ^ {2}}} = {\ frac {(\ Дельта \ nu _ {c}) ^ {2}} {(\ Delta \ nu _ {c}) ^ {2} +4 (\ nu - \ nu _ {q}) ^ {2}}}.}

{\ displaystyle \ gamma _ {q, L} (\ ню) = {\ гидроразрыва {\ пи} {2}} \ Delta \ nu _ {c} {\ tilde {\ gamma}} _ {q} (\ nu) = {\ frac { (\ Delta \ nu _ {c} / 2) ^ {2}} {(\ Delta \ nu _ {c} / 2) ^ {2} + (\ nu - \ nu _ {q}) ^ {2} }} = {\ frac {(\ Delta \ nu _ {c}) ^ {2}} {(\ Delta \ nu _ {c}) ^ {2} +4 (\ nu - \ nu _ {q}) ^ {2}}}.}

При повторении вышеуказанного преобразования Фурье для всех режимов с индексом моды $q {\ displaystyle q}$ $q$ в резонаторе один получает полный модовый спектр резонатора.

ширина линии $Δ ν c {\ displaystyle \ Delta \ nu _ {c}}$ ${\ displaystyle \ Delta \ nu _ {c}}$ и свободный спектральный диапазон $Δ ν FSR {\ displaystyle \ Delta \ nu _ {\ rm {FSR}}}$ ${\ displaystyle \ Delta \ nu _ {\ rm {FSR} }}$ не зависит от частоты, тогда как в длинных волнах линии не может быть правильно определена, а свободный спектральный диапазон зависит от длины волны, и поскольку резонансные частоты $ν q {\ displaystyle \ nu _ {q}}$ ${\ displaystyle \ nu _ {q}}$ В масштабе, пропорциональном частот, спектральный отклик резонатора Фабри-Перо естественным образом анализируется и отображается в частотном пространстве.

Общее распределение Эйри: коэффициент усиления внутреннего резонанса

Электрические поля в резонаторе Фабри-Перо. Коэффициент отражения электрического поля зеркала равенства

r 1 {\ displaystyle r_ {1}}

r_1

r 2 {\ displaystyle r_ {2}}

r_2

. Указанные характерные электрические поля, создаваемые электрические полем

E inc {\ displaystyle E _ {\ rm {inc}}}

{\ displaystyle E _ {\ rm {inc}}}

, падающим на зеркало 1:

E refl, 1 {\ displaystyle E_ { \ rm {refl, 1}}}

{\ displaystyle E _ {\ rm {refl, 1}}}

установлен отраженный в зеркале 1,

E laun {\ displaystyle E _ {\ rm {laun}}}

{\ displaystyle E _ {\ rm {laun}}}

запущен через зеркало 1,

E circ {\ displaystyle E _ {\ rm {circ}}}

{\ displaystyle E _ {\ rm {circ}}}

E b-circ {\ displaystyle E _ {\ text {b-circ}}}

{\ displaystyle E _ {\ text {b-circ}} }

циркулирует внутри резонатора в прямом и обратном направлениях соответственно,

ERT {\ displaystyle E _ {\ rm {RT}}}

{\ displaystyle E _ {\ rm {RT}}}

распространяется внутри резонатора после одного обхода,

E trans {\ displaystyle E _ {\ rm {trans}}}

{\ displaystyle E _ {\ rm {trans}}}

передается через зеркало 2,

E back {\ displaystyle E _ {\ rm {back}}}

{\ displaystyle E _ { \ rm {назад}}}

передается через зеркало 1, а общее поле

E refl {\ displaystyle E _ {\ rm {refl}}}

{\ displaystyle E _ {\ rm {refl}} }

распространяется в обратном направлении. Интерференция возникает с левой и правой сторон зеркала 1 между

E refl, 1 {\ displaystyle E _ {\ rm {refl, 1}}}

{\ displaystyle E _ {\ rm {refl, 1}}}

E back {\ displaystyle E _ { \ rm {back}}}

{\ displaystyle E _ { \ rm {назад}}}

, в результате получается

E refl {\ displaystyle E _ {\ rm {refl}}}

{\ displaystyle E _ {\ rm {refl}} }

, а между

E laun { \ displaystyle E _ {\ rm {laun}}}

{\ displaystyle E _ {\ rm {laun}}}

ERT {\ displaystyle E _ {\ rm {RT}}}

{\ displaystyle E _ {\ rm {RT}}}

, в результате получается

E circ {\ displaystyle E _ {\ rm {circ}}}

{\ displaystyle E _ {\ rm {circ}}}

соответственно.

Реакция резонатора Фабри-Перо на электрическое поле, падающее на зеркало 1, описывается распределениями Эйри (названными в честь математика и астроном Джордж Бидделл Эйри ), которые количественно определяют интенсивность света в прямом или обратном направлении пространства в различных параметров положения в параметрах выпущенного или вне резонатора. Отклик резонатора Фабри-Перо легче всего получить с помощью метода циркулирующего поля. Этот подход предполагает установившееся состояние и связывает электрические поля друг с другом (см. Рисунок «Электрические поля в резонаторе Фабри-Перо»).

Поле $E circ {\ displaystyle E _ {\ rm {circ}}}$ ${\ displaystyle E _ {\ rm {circ}}}$ может быть связано с полем $E laun {\ displaystyle E _ {\ rm { Laun}}}$ ${\ displaystyle E _ {\ rm {laun}}}$ , который запускается в резонатор с помощью

E circ = E laun + ERT = E laun + r 1 r 2 e - i 2 ϕ E circ ⇒ E circ E laun = 1 1 - r 1 r 2 e - i 2 ϕ. {\ displaystyle E _ {\ rm {circ}} = E _ {\ rm {laun}} + E _ {\ rm {RT}} = E _ {\ rm {laun}} + r_ {1} r_ {2 } e ^ {-i2 \ phi} E _ {\ rm {circ}} \ Rightarrow {\ frac {E _ {\ rm {circ}}} {E _ {\ rm {laun}}}} = {\ frac {1} {1-r_ {1} r_ {2} e ^ {- i2 \ phi}}}.}

{\ displaystyle E _ {\ rm {circ}} = E _ {\ rm {laun}} + E _ {\ rm {RT}} = E _ {\ rm {l aun}} + r_ {1} r_ {2} e ^ {- i2 \ phi} E _ {\ rm {circ}} \ Rightarrow { \ frac {E _ {\ rm {circ}}} {E _ {\ rm {laun}}}} = {\ frac {1} {1-r_ {1} r_ {2} e ^ {- i2 \ phi }}}.}

Общее распределение Эйри, которое учитывает только физические процессы, проявляющиеся светом внутри резонатора, определяет как интенсивность, циркулирующая в резонаторе, относительно к запускаемой интенсивности,

A circ = I circ I laun = | E c i r c | 2 | Э л а у н | 2 = 1 | 1 - r 1 r 2 e - i 2 ϕ | 2 = 1 (1 - R 1 R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ). {\ displaystyle A _ {\ rm {circ}} = {\ frac {I _ {\ rm {circ}}} {I _ {\ rm {laun}}}} = {\ frac {\ left | E _ {\ rm {circ}} \ right | ^ {2}} {\ left | E _ {\ rm {laun}} \ right | ^ {2}}} = {\ frac {1} {\ left | 1-r_ {1} r_ {2} e ^ {- i2 \ phi} \ right | ^ {2}}} = {\ frac {1} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ { 1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

{\ displaystyle A _ {\ rm {circ}} = {\ frac {I_ {\ rm {circ}}} {I _ {\ rm {laun}}}} = {\ frac {\ left | E _ {\ rm {circ}} \ right | ^ {2}} {\ left | E _ {\ rm {laun}} \ right | ^ {2}}} = {\ frac {1} {\ left | 1-r_ {1} r_ {2} e ^ {- i2 \ phi} \ right | ^ {2}}} = {\ frac {1} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ { 1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

$Цикл {\ displaystyle A _ {\ rm {circ}}}$ ${\ displaystyle A _ {\ rm {circ}}}$ представляет спектрально зависимое усиление внутреннего резонанс, который резонатор обеспечивает свету, который в него попадает (см. Рисунок «Усиление резонанса в резонаторе Фабри-Перо»). На резонансных частотах $ν q {\ displaystyle \ nu _ {q}}$ ${\ displaystyle \ nu _ {q}}$ , где $sin ⁡ (ϕ) {\ displaystyle \ sin (\ phi)}$ ${\ displaystyle \ sin (\ phi)}$ равно нулю, коэффициент усиления внутреннего резонанса равен

A circ (ν q) = 1 (1 - R 1 R 2) 2. {\ displaystyle A _ {\ rm {circ}} (\ nu _ {q}) = {\ frac {1} {\ left (1 - {\ sqrt {R_ {1} R_ {2}}} \ right) ^ {2}}}.}

{\ displaystyle A _ {\ rm {circ}} (\ nu _ {q}) = {\ frac {1} {\ left (1 - {\ sqrt {R_ {1} R_ {2}}} \ right) ^ {2}}}.}

Другие распределения Эри

Резонансное усиление в резонаторе Фабри-Перо. (вверху) Спектрально-зависимое усиление внутреннего резонанса, равное общему распределению Эйри

A circ {\ displaystyle A _ {\ text {circ}}}

{\ displaystyle A_ {\ text {circ}}}

. Свет, попадающий в резонатор, резонансно усиливается этим фактором. Для кривой с

R 1 = R 2 = 0,9 {\ displaystyle R_ {1} = R_ {2} = 0,9}

{\ displaystyle R_ {1} = R_ {2} = 0,9}

пиковое значение находится на

Круг (ν q) = 100 {\ displaystyle A _ {\ text {circ}} (\ nu _ {q}) = 100}

{\ displaystyle A _ {\ text {circ}} (\ nu _ {q}) = 100}

, вне шкалы ординат. (внизу) Спектрально зависимое усиление внешнего резонанса, равное распределение Эйри

A circ '{\ displaystyle A _ {\ text {circ}} ^ {\ prime}}

{\ displaystyle A _ {\ text {circ}} ^ {\ prime}}

. Свет, падающий на резонатор, резонансно усиливается этим фактором.

После того, как установлено усиление внутреннего резонанса, общее распределение Эйри, все остальные распределения Эйри могут быть выведены с помощью простых масштабных коэффициентов. Интенсивность, вводимая в резонатор, равна переданной части, падающая на зеркало 1,

I laun = (1 - R 1) I inc, {\ displaystyle I _ {\ text {laun}} = \ left (1 - R_ {1} \ right) I _ {\ text {inc}},}

{\ displaystyle I _ {\ text {laun}} = \ left (1-R_ {1} \ right) I _ {\ text {inc}},}

и интенсивности, прошедшие через зеркало 2, отраженные от зеркала 2 и прошедшие через зеркало 1, меньше себя прошедшие и отраженные / прошедшие доли мощности циркулирует внутри резонатора,

I trans = (1 - R 2) I circ, I b-circ = R 2 I circ, I back = (1 - R 1) I b-circ, {\ displaystyle {\ begin {выровнено} I _ {\ text {trans}} = \ left (1-R_ {2} \ right) I _ {\ text {circ}}, \\ I _ {\ text {b-circ}} = R_ { 2} I _ {\ text {circ}}, \\ I _ {\ text {back}} = \ left (1-R_ {1} \ right) I _ {\ text {b-circ}}, \ end {выровнено}}

{\ displaystyle {\ begin {align} I _ {\ text {trans}} = \ left (1-R_ {2} \ right) I _ {\ text {circ}}, \\ I _ {\ text {b-circ}} = R_ {2} I _ {\ text {circ}}, \\ I _ {\ text {back}} = \ left ( 1-R_ {1} \ right) I _ {\ text {b-circ}}, \ end {align}}}

соответственно, другие дистрибутивы Эйри $A {\ displaystyle A}$ $A$ в отношении запуска $Я запускаю {\ displaystyle I _ {\ text {laun}} }$ ${\ displaystyle I _ {\ text {laun}}}$ и $A ′ {\ displaystyle A ^ {\ prime} }$ ${\ displaystyle A ^ {\ prime}}$ относительно падающего излучения $I в c {\ displaystyle I _ {\ text {inc}}}$ ${\ displaystyle I _ {\ текст {inc}}}$ равны

A circ = 1 R 2 A b-circ = 1 R 1 R 2 A RT = 1 1 - R 2 A trans = 1 (1 - R 1) R 2 A назад = 1 1 - R 1 R 2 A излучение, A circ ′ = 1 R 2 A b-circ ′ = 1 R 1 R 2 A RT ′ = 1 1 - R 2 A trans ′ = 1 (1 - R 1) R 2 A back ′ = 1 1 - R 1 R 2 A emit ′, A circ ′ = (1 - R 1) А круг. {\ displaystyle {\ begin {align} A _ {\ text {circ}} = {\ frac {1} {R_ {2}}} A _ {\ text {b-circ}} = {\ frac {1 } {R_ {1} R_ {2}}} A _ {\ text {RT}} = {\ frac {1} {1-R_ {2}}} A _ {\ text {trans}} = {\ frac {1} {(1-R_ {1}) R_ {2}}} A _ {\ text {back}} = {\ frac {1} {1-R_ {1} R_ {2}}} A _ { \ text {emit}}, \\ A _ {\ text {circ}} '= {\ frac {1} {R_ {2}}} A _ {\ text {b-circ}}' = {\ frac {1} {R_ {1} R_ {2}}} A _ {\ text {RT}} '= {\ frac {1} {1-R_ {2}}} A _ {\ text {trans}}' = {\ frac {1} {(1 -R_ {1}) R_ {2}}} A _ {\ text {back}} '= {\ frac {1} {1-R_ {1} R_ {2} }} A _ {\ text {emit}} ', \\ A _ {\ text {circ}}' = \ left (1-R_ {1} \ right) A _ {\ text {circ}}. \ End {align}}}

{\begin{aligned}A_{\text{circ}}={\frac {1}{R_{2}}}A_{\text{b-circ}}={\frac {1}{R_{1}R_{2}}}A_{\text{RT}}={\frac {1}{1-R_{2}}}A_{\text{trans}}={\frac {1}{(1-R_{1})R_{2}}}A_{\text{back}}={\frac {1}{1-R_{1}R_{2}}}A_{\text{emit}},\\A_{\text{circ}}'={\frac {1}{R_{2}}}A_{\text{b-circ}}'={\frac {1}{R_{1}R_{2}}}A_{\text{RT}}'={\frac {1}{1-R_{2}}}A_{\text{trans}}'={\frac {1}{(1-R_{1})R_{2}}}A_{\text{back}}'={\frac {1}{1-R_{1}R_{2}}}A_{\text{emit}}',\\A_{\text{circ}}'=\left(1-R_{1}\right)A_{\text{circ}}.\end{aligned}}

Индекс "emit" обозначает распределение Эйри, которые рассматривают объем интенсивностей, излучаемых с разных сторон резонатора.

Интенсивность обратного прохода $Я вернулся {\ displaystyle I _ {\ text {back}}}$ ${\ displaystyle I _ {\ text {back}}}$ не может быть измерена, потому что также используется отраженный назад свет добавлен к обратному свету. - распространяющийся сигнал. Измеримый случай силы, возникающий в результате интерференции обоих распространяющихся в обратном направлении электрических полей, приводит к распределению Эйри

A refl ′ = I refl I inc = | E refl | 2 | E inc | 2 = (R 1 - R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ) (1 - R 1 R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ). {\ displaystyle A _ {\ text {refl}} ^ {\ prime} = {\ frac {I _ {\ text {refl}}} {I _ {\ text {inc}}}} = {\ frac {\ слева | E_ {\ text {refl}} \ right | ^ {2}} {\ left | E _ {\ text {inc}} \ right | ^ {2}}} = {\ frac {\ left ({{\ sqrt {R_ {1}}} - {\ sqrt {R_ {2}}}} \ right) ^ {2} +4 {\ sqrt { R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

{\ displaystyle A _ {\ text {refl}} ^ {\ prime} = {\ frac {I _ {\ text {refl}}} {I _ {\ text {inc}}}} = {\ frac {\ left | E _ {\ text {refl}} \ right | ^ {2}} {\ left | E _ {\ text {inc}} \ right | ^ {2}}} = {\ frac {\ left ({{\ sqrt {R_ {1}}} - {\ sqrt {R_ {2}}}} \ right) ^ {2} +4 {\ sqrt { R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

Легко показать, что в резонаторе Фабри-Перо, несмотря на возникновение конструктивной и деструктивной интерференции, энергия сохраняется на всех частотах:

A trans '+ A refl ′ = I trans + I refl I inc = 1. {\ displaystyle A _ {\ text {trans}} ^ {\ prime} + A _ {\ text {refl}} ^ {\ prime} = {\ frac {I_ {\ text {trans}} + I _ {\ text {refl}}} {I _ {\ text {inc}}}} = 1.}

{\ displaystyle A _ {\ text {trans}} ^ {\ prime} + A _ {\ text {refl}} ^ {\ prime} = {\ frac {I _ {\ text {trans}} + I _ {\ text {refl}}} {I _ {\ text {inc}}}} = 1.}

Коэффициент усиления внешнего резонанса (см. Рисунок «Повышение резонанса в аппарате Фабри-Перо резонатор») равно

A circ ′ = I circ I inc = (1 - R 1) A circ = 1 - R 1 (1 - R 1 R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ). {\ Displaystyle A _ {\ text {circ}} ^ {\ prime} = {\ frac {I _ {\ text {circ} }} {I _ {\ text {inc}}}} = (1-R_ {1}) A _ {\ text {circ}} = {\ frac {1-R_ {1}} {\ влево ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} + 4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} ( \ phi)}}.}

{\ displaystyle A_ {\ text {circ}} ^ {\ prime} = {\ frac {I _ {\ текст {circ}}} {I _ {\ text {inc}}}} = (1-R_ {1}) A _ {\ text {circ}} = {\ frac {1-R_ {1}} {\ влево ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} ( \ phi)}}.}

На резонансных частотах $ν q {\ displaystyle \ nu _ {q}}$ ${\ displaystyle \ nu _ {q}}$ , где $sin ⁡ (ϕ) {\ displaystyle \ sin ( \ phi)}$ ${\ displaystyle \ sin (\ phi)}$ равенство нулю, коэффициент усиления внешнего резонанса равен

A circ ′ (ν q) = 1 - R 1 (1 - R 1 R 2) 2. {\ displaystyle A _ {\ текст {circ}} ^ {\ prime} (\ nu _ {q}) = {\ frac {1-R_ {1}} {\ left (1 - {\ sqrt {R_ {1}) R_ {2}}) } \ right) ^ {2}}}.}

{\ displaystyle A _ {\ text {circ}} ^ {\ prime} (\ nu _ {q}) = {\ frac {1-R_ {1}} {\ left (1 - {\ sqrt {R_ {1} R_ {2}}} \ right) ^ {2}}}.}

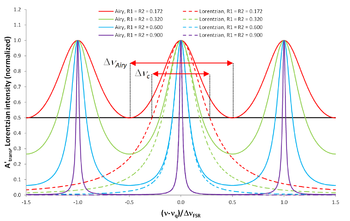
Распределение Эйри

A транс '{\ displaystyle A _ {\ text {trans}} ^ {\ prime}}

{\ displaystyle A_ {\ text {trans}} ^ {\ prime}}

(сплошные линии), соответствующий свету, проходящему через резонатор Фабри-Перо, рассчитанному для различных значений коэффициентов отражения

R 1 = R 2 {\ displaystyle R_ {1} = R_ {2}}

{\ displaystyle R_ {1} = R_ { 2}}

, и сравнение с одной лоренцевой линией (пунктирные линии), рассчитанной для того же

R 1 = R 2 {\ displaystyle R_ {1} = R_ {2}}

{\ displaystyle R_ {1} = R_ { 2}}

. На половину линии (черная линия) с уменьшением коэффициентов отражения ширины линии на полувысоте

Δν Эйри {\ displaystyle \ Delta \ nu _ {\ text {Airy}}}

{\ displaystyle \ Delta \ nu _ {\ text {Эйри }}}

распределения Эйри расширяется по сравнению с шириной линии на полувысоте

Δ ν c {\ displaystyle \ Delta \ nu _ {c}}

{\ displaystyle \ Delta \ nu _ {c}}

формирует лоренцевой линии:

R 1 = R 2 = 0,9, 0,6, 0, 32, 0,172 {\ displaystyle R_ {1} = R_ {2} = 0.9,0.6,0.32,0.172}

{\ displaystyle R_ {1} = R_ {2} = 0.9,0.6,0.32,0.172}

дает

Δ ν Эйри / Δ ν c = 1.001, 1.022, 1.132, 1.717 { \ displaystyle \ Delta \ nu _ {\ text {Airy}} / \ Delta \ nu _ {c} = 1.001,1.022,1.132,1.717}

{\ displaystyle \ Delta \ nu _ {\ text {Эйри}} / \ Delta \ nu _ {c} = 1.001,1.022,1.132,1.717}

соответственно.

Обычно свет проходит через резонатор Фабри-Перо. Следовательно, часто используется распределение Эйри:

A trans '= I trans I inc = (1 - R 1) (1 - R 2) A circ = (1 - R 1) (1 - R 2) (1 - R 1 R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ). {\ displaystyle A _ {\ text {trans}} ^ {\ prime} = {\ frac {I _ {\ text {trans}}} {I _ {\ text {inc}}}} = (1-R_ { 1}) (1-R_ {2}) A _ {\ text {circ}} = {\ frac {(1-R_ {1}) (1-R_ {2})} {\ left ({1 - { \ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}}. }

{\ displaystyle A _ {\ text {trans}} ^ {\ prime} = {\ frac {I _ {\ text {trans }}} {I _ {\ text {inc}}}} = (1-R_ {1}) (1-R_ {2}) A _ {\ text {circ}} = {\ frac {(1-R_ {1}) (1-R_ {2})} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ { 1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

Он в роли $Я транс {\ displaystyle I _ {\ text {trans}}}$ ${\ displaystyle I _ { \ text {trans}}}$ интенсивности $I inc {\ displaystyle I _ {\ text {inc}}}$ ${\ displaystyle I _ {\ текст {inc}}}$ источник света, падающего на зеркало 1, который проходит через зеркало 2 (см. Рисунок «Распределение Эйри $Транс '{\ displaystyle A _ {\ text {trans}} ^ {\ prime}}$ ${\ displaystyle A_ {\ text {trans}} ^ {\ prime}}$ "). Его пиковое значение на резонансных частотах $ν q {\ displaystyle \ nu _ {q}}$ ${\ displaystyle \ nu _ {q}}$ равно

A trans ′ (ν q) = (1 - R 1) (1 - R 2) (1 - К 1 К 2) 2. {\ displaystyle A _ {\ text {trans}} ^ {\ prime} (\ nu _ {q}) = {\ frac { (1-R_ {1}) (1-R_ {2})} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2}}}.}

{\ displaystyle A _ {\ text {trans}} ^ {\ prime} (\ nu _ {q}) = {\ frac {(1-R_ { 1}) (1-R_ {2})} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2}}}.}

Для $R 1 = R 2 {\ displaystyle R_ {1} = R_ {2} }$ ${\ displaystyle R_ {1} = R_ { 2}}$ пиковое значение равно единице, т. Е. Весь свет, падающий на резонатор, проходит; следовательно, свет не отражается, $A refl ′ = 0 {\ displaystyle A _ {\ text {refl}} ^ {\ prime} = 0}$ ${\ displaystyle A _ {\ text {refl}} ^ {\ prime} = 0}$ , в результате деструктивного взаимодействия между полями $E refl, 1 {\ displaystyle E _ {{\ text {refl}}, 1}}$ ${\ displaystyle E _ {{\ text {refl}}, 1}}$ и $E back {\ displaystyle E _ {\ text {back}}}$ ${\ displaystyle E _ {\ text {back}}}$ .

$Транс '{\ displaystyle A _ {\ text {trans}} ^ {\ prime}}$ ${\ displaystyle A_ {\ text {trans}} ^ {\ prime}}$ был получен в подходе с циркулирующим полем с учетом дополнительного фазового сдвига $ei π / 2 {\ displaystyle e ^ { i \ pi / 2}}$ ${\ displaystyle e ^ {i \ pi / 2}}$ во время каждой передачи через зеркало,

E circ = it 1 E inc + r 1 r 2 e - i 2 ϕ E circ ⇒ E circ E inc = it 1 1 - r 1 r 2 e - i 2 ϕ, E trans = it 2 E circ e - i ϕ ⇒ E trans E inc = - t 1 t 2 e - i ϕ 1 - r 1 r 2 e - я 2 ϕ, {\ displaystyle {\ begin {align} E _ {\ text {circ}} = it_ {1} E _ {\ text {inc}} + r_ {1} r_ {2} e ^ {- i2 \ phi} E _ {\ text {circ}} \ Rightarrow {\ frac {E _ {\ text {circ}}} {E _ {\ text {inc}}}} = {\ frac {it_ {1}} {1- r_ {1} r_ {2} e ^ {- i2 \ phi}}}, \\ E _ {\ text {trans}} = it_ {2} E _ {\ text {circ}} e ^ {- i \ phi} \ Rightarrow {\ f rac {E _ {\ text {trans}}} {E _ {\ text {inc}}}} = {\ frac {-t_ {1} t_ {2} e ^ {- i \ phi}} {1-r_ {1} r_ {2} e ^ {- i2 \ phi }}}, \ end {align}}}

{\ displaystyle { \ begin {align} E _ {\ text {circ}} = it_ {1} E _ {\ text {inc}} + r_ {1} r_ {2} e ^ {- i2 \ phi} E _ {\ текст {circ}} \ Rightarrow {\ frac {E _ {\ text {circ}}} {E _ {\ text {inc}}}} = {\ frac {it_ {1}} {1-r_ {1} r_ {2} e ^ {- i2 \ phi}}}, \\ E _ {\ text {trans}} = it_ {2} E _ {\ text {circ}} e ^ {-i \ phi} \ Стрелка вправо {\ frac {E _ {\ text {trans}}} {E _ {\ text {inc}}}} = {\ frac {-t_ {1} t_ {2} e ^ {- i \ phi}} {1-r_ {1} r_ {2} e ^ {- i2 \ phi}}}, \ end {align}}}

, что дает

A trans ′ = I trans I inc = | E транс | 2 | E inc | 2 = | - t 1 t 2 e - i ϕ | 2 | 1 - r 1 r 2 e - i 2 ϕ | 2 = (1 - R 1) (1 - R 2) (1 - R 1 R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ). {\ displaystyle A _ {\ text {trans}} ^ {\ prime} = {\ frac {I _ {\ text {trans}}} {I _ {\ text {inc}}}} = {\ frac {\ слева | E_ {\ text {trans}} \ right | ^ {2}} {\ left | E _ {\ text {inc}} \ right | ^ {2}}} = {\ frac {\ left | -t_ {1} t_ {2} e ^ {- i \ phi} \ right | ^ {2}} {\ left | 1-r_ {1} r_ {2} e ^ {- i2 \ phi} \ right | ^ {2}}} = {\ frac {(1-R_ {1}) (1-R_ {2})} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}}) \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

{\ displaystyle A _ {\ text {trans}} ^ {\ prime} = {\ frac {I _ {\ text {trans}}} {I _ {\ текст {inc}}}} = {\ frac {\ left | E _ {\ text {trans}} \ right | ^ {2}} {\ left | E _ {\ text {inc}} \ right | ^ {2}}} = {\ frac {\ left | -t_ {1} t_ {2} e ^ {- i \ phi} \ right | ^ {2}} {\ left | 1-r_ {1} r_ {2} e ^ {- i2 \ phi} \ right | ^ {2}}} = {\ frac {(1-R_ {1}) (1- R_ {2})} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}}.}

В качестве альтернативы, $транс '{ \ displaystyle A _ {\ text {trans}} ^ {\ prime}}$ ${\ displaystyle A_ {\ text {trans}} ^ {\ prime}}$ может быть получен с помощью метода распада туда и обратно, отслеживая бесконечное количество циклов, которые падающее электрическое поле $E inc {\ displaystyle E _ {\ text {inc}}}$ ${\ displaystyle E _ {\ текст {inc}}}$ проявляется после входа в резонатор и накопления электрического поля $E trans {\ displaystyle E _ {\ text {trans}}}$ ${\ displaystyle E _ {\ text {trans}}}$ передается во всех круговых обходах. Поле, передаваемое после первого распространения, и все меньшие и меньшие поля, передаваемые после каждого последовательного поля через резонатор, равны

E trans, 1 = E inc it 1 it 2 e - i ϕ = - E inc t 1 t 2 e - я ϕ, E транс, m + 1 = E транс, mr 1 r 2 e - я 2 ϕ, {\ displaystyle {\ begin {align} E _ {\ text {trans, 1}} = E _ {\ текст {inc}} it_ {1} it_ {2} e ^ {- i \ phi} = - E _ {\ text {inc}} t_ {1} t_ {2} e ^ {- i \ phi}, \ \ E _ {{\ text {trans}}, m + 1} = E _ {{\ text {trans}}, m} r_ {1} r_ {2} e ^ {- i2 \ phi}, \ end {align}}}

{\ displaystyle {\ begin { выровнено} E _ {\ text {trans, 1}} = E _ {\ text {inc}} it_ {1} it_ {2} e ^ {- i \ phi} = - E _ {\ text {inc} } t_ {1} t_ {2} e ^ {- i \ phi}, \\ E _ {{\ text {trans}}, m + 1} = E _ {{\ text {trans}}, m} r_ {1} r_ {2} e ^ {- i2 \ phi}, \ end {align}}}

соответственно. Использование

∑ m = 0 ∞ xm = 1 1 - x ⇒ E trans = ∑ m = 1 ∞ E trans, m = E inc - t 1 t 2 e - i ϕ 1 - r 1 r 2 e - i 2 ϕ {\ displaystyle \ sum _ {m = 0} ^ {\ infty} x ^ {m} = {\ frac {1} {1-x}} \ Rightarrow E _ {\ text {trans}} = \ sum _ {m = 1} ^ {\ infty} E _ {{\ text {trans}}, m} = E _ {\ text {inc}} {\ frac {-t_ {1} t_ {2} e ^ {- я \ phi}} {1-r_ {1} r_ {2} e ^ {- i2 \ phi}}}}

{\ displaystyle \ sum _ {m = 0 } ^ {\ infty } x ^ {m} = {\ frac {1} {1-x}} \ Rightarrow E _ {\ text {trans}} = \ sum _ {m = 1} ^ {\ infty} E _ {{\ text {trans}}, m} = E _ {\ text {inc}} {\ frac {-t_ {1} t_ {2} e ^ {- i \ phi}} {1-r_ {1} r_ {2} е ^ {- i2 \ phi}}}}

дает тот же результат $E trans / E inc {\ displaystyle E _ {\ text {trans}} / E _ {\ text {inc}}}$ ${\ displaystyle E _ {\ text {trans}} / E _ {\ text {inc}}}$ , как указано выше, поэтому такое же распределение Эйри $A trans '{\ displaystyle A _ {\ text {trans}} ^ {\ prime}}$ ${\ displaystyle A_ {\ text {trans}} ^ {\ prime}}$ происходит. Однако этот подход вводит в заблуждение с физической точки зрения, поскольку он предполагает, что интерференция имеет место между выведенными лучами после зеркала 2, вне резонатора, а не между выпущенными и циркулирующими лучами после зеркала 1 внутри резонатора. Пропадающего излучения, и никакого усиления резонанса внутри не происходит, когда используется именно интерференция, изменяет спектральный состав, распределение спектральной силы внутри резонатора таким образом.

Распределение Эйри как сумма профилей мод

Физически распределение Эйри представляет собой сумму профилей мод продольных мод резонатора. Исходя из этого электрического поля $E {\ displaystyle E_ {circ}}$ ${\ displaystyle E_ {circ}}$ , циркулирующего внутри резонатора, мы рассматриваем экспоненциальное затухание во времени поля через оба зеркала резонатора, Фурье преобразует его в частотное пространство для нормализованных форм спектральных линий $γ ~ q (ν) {\ displaystyle {\ tilde {\ gamma}} _ {q} (\ nu)}$ ${\ displaystyle {\ тильда {\ гамма}} _ {q} (\ ню)}$ , делит его на круг -время срабатывания $t RT {\ displaystyle t _ {\ rm {RT}}}$ ${\ displaystyle t _ {\ rm {RT}}}$ для учета того, как полная циркулирующая напряженность электрического поля распределяется в продольном направлении в резонаторе и выводится за единицу времени, в результате чего получаются профили излучаемых режимов 672>γ q, испускать (ν) знак равно 1 t RT γ ~ q (ν), {\ displaystyle \ gamma _ {q, {\ rm {emit}}} (\ nu) = {\ frac {1} {t_ {\ rm {RT}}}} {\ tilde {\ gamma}} _ {q} (\ nu),} ${\ displaystyle \ gamma _ {q, {\ rm {emit}}} (\ Nu) = {\ гидроразрыва {1} {t _ {\ rm {RT}}}} {\ tilde {\ gamma}} _ {q} (\ nu),}$

, а затем суммирует профили излучаемых мод всех продольных мод

∑ q = - ∞ ∞ γ q, излучение (ν) = 1 - R 1 R 2 (1 - R 1 R 2) 2 + 4 R 1 R 2 sin 2 ⁡ (ϕ) = A испускать, {\ displaystyle \ sum _ {q = - \ infty} ^ {\ infty} \ gamma _ {q, {\ rm {emit}}} (\ nu) = {\ frac {1-R_ {1} R_ {2}} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}} = A _ {\ rm {emit}},}

{\ displaystyle \ sum _ {q = - \ infty} ^ {\ infty} \ gamma _ {q, {\ rm {emit}}} (\ nu) = {\ frac {1-R_ {1} R_ {2}} {\ left ({1 - { \ sqrt {R_ {1} R_ {2}}}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} \ sin ^ {2} (\ phi)}} = A_ {\ rm {emit}},}

, что равняется распределению Эйри $A emit {\ displaystyle A _ {\ rm {emit}}}$ ${\ displaystyle A _ {\ rm {emit}}}$ .

Те же простые коэффициенты масштабирования, которые обеспечивают отношения между отдельными распределениями Эйри, также обеспечивают отношения между $γ q, emit (ν) {\ displaystyle \ gamma _ {q, {\ rm {emit}}} (\ nu) }$ ${\ displaystyle \ gamma _ {q, {\ rm {emit}}} ( \ nu)}$ и другие профили режима:

γ q, circ = 1 R 2 γ q, b-circ = 1 R 1 R 2 γ q, RT = 1 1 - R 2 γ q, trans Знак равно 1 (1 - R 1) р 2 γ q, назад = 1 1 - R 1 R 2 γ q, испускать, {\ displaystyle \ gamma _ {q, {\ rm {circ}}} = {\ frac {1 } {R_ {2}}} \ gamma _ {q, {\ text {b-circ}}} = {\ frac {1} {R_ {1} R_ {2}}} \ gamma _ {q, {\ rm {RT}}} = {\ frac {1} {1-R_ {2}}} \ gamma _ {q, {\ rm {trans}}} = {\ frac {1} {(1-R_ {1 }) R_ {2}}} \ gamma _ {q, {\ rm {back}}} = {\ frac {1} {1-R_ {1} R_ {2}}} \ gamma _ {q, {\ rm {emit}}},}

{\ displaystyle \ gamma _ {q, {\ rm {circ}}} = {\ frac {1} {R_ {2}} } \ gamma _ {q, {\ text {b-circ}}} = {\ frac {1} {R_ {1} R_ {2}}} \ gamma _ {q, {\ rm {RT}}} = {\ frac {1} {1-R_ {2}}} \ gamma _ {q, {\ rm {trans}}} = {\ frac {1} {(1-R_ {1}) R_ {2}} } \ gamma _ {q, {\ rm {back}}} = {\ frac {1} {1-R_ {1} R_ {2}}} \ gamma _ {q, {\ rm {emit}}}, }

γ q, circ ′ = 1 R 2 γ q, b-circ ′ = 1 R 1 R 2 γ q, RT ′ = 1 1 - R 2 γ q, trans ′ = 1 (1 - R 1) R 2 γ q, назад ′ = 1 1 - R 1 R 2 γ q, испускать ′, {\ displaystyle \ gamma _ {q, {\ rm {circ}}} ^ {\ prime} = {\ frac {1} {R_ {2}}} \ gamma _ {q, {\ text {b-circ}}} ^ {\ prime} = {\ frac {1} {R_ {1} R_ {2}}} \ gamma _ {q, {\ rm {RT}}} ^ {\ prime} = {\ frac {1} {1-R_ {2}}} \ gamma _ {q, {\ rm {trans}}} ^ {\ prime} = {\ frac {1} {(1 -R_ {1}) R_ {2}}} \ gamma _ {q, {\ rm {back}}} ^ {\ prime} = {\ frac {1} {1-R_ {1} R_ {2}} } \ gamma _ {q, {\ rm {emit}}} ^ {\ prime},}

{\ displaystyle \ gamma _ {q, {\ rm {circ}}} ^ {\ prime} = {\ frac {1} {R_ {2}}} \ gamma _ {q, {\ text {b-circ}}} ^ {\ prime} = {\ frac {1} {R _ {1} R_ {2}}} \ gamma _ {q, {\ rm {RT}}} ^ {\ prime} = {\ frac {1} {1-R_ {2}}} \ gamma _ {q, {\ rm {trans}}} ^ {\ prime} = {\ frac {1} {(1-R_ {1}) R_ {2}}} \ gamma _ {q, {\ rm {back}}} ^ {\ prime} = {\ frac {1} {1- R_ {1} R_ {2}}} \ gamma _ {q, {\ rm {emit}}} ^ {\ prime},}

γ q, circ ′ = (1 - R 1) γ q, cir c. {\ displaystyle \ gamma _ {q, {\ rm {circ}}} ^ {\ prime} = (1-R_ {1}) \ gamma _ {q, {\ rm {circ}}}.}

{\ displaystyle \ gamma _ {q, {\ rm {circ}}} ^ {\ prime} = (1-R_ {1}) \ gamma _ {q, {\ rm {circ}}}.}

Характеристика резонатора Фабри-Перо: лоренцевская ширина линии и точности

Критерий спектрального разрешения Тейлора предполагает, что две спектральные линии могут быть разрешены, если отдельные линии пересекаются с половинной интенсивностью. Запуская свет в резонатор Фабри-Перо, измеряя размер Эйри, можно получить полные потери путем пересчета лоренцевой ширины линии $Δ ν c {\ displaystyle \ Delta \ nu _ {c}}$ ${\ displaystyle \ Delta \ nu _ {c}}$ , отображает (синяя линия) относительно свободного спектрального диапазона на рисунке «Лоренцева ширина линии и четкость в зависимости от ширины линии Эйри и четкости резонатора Фабри-Перо».

Лоренцевская ширина линии и точность в зависимости от ширины линии по Эйри и точность резонатора Фабри-Перо. [Слева] Относительная ширина лоренцевой линии

Δ ν c / Δ ν FSR {\ displaystyle \ Delta \ nu _ {c} / \ Delta \ nu _ {\ rm {FSR}}}

{\ displaystyle \ Delta \ nu _ {c} / \ Delta \ nu _ {\ rm {FSR}}}

(синяя кривая), относительная ширина линии Эйри

Δ ν A iry / Δ ν FSR {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} / \ Delta \ nu _ {\ rm {FSR}}}

{\ displaystyle \ Delta \ nu _ {\ rm {Airy}} / \ Delta \ nu _ {\ rm {FSR}}}

(зеленая кривая) и его аппроксимация (красная кривая). [Справа] Лоренцевское изящество

F c {\ displaystyle {\ mathcal {F}} _ {c}}

{\ Displaystyle {\ math cal {F}} _ {c}}

(синяя кривая), Эйри изящество

FA iry {\ displaystyle {\ mathcal { F}} _ {\ rm {Airy}}}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Эйри}}}

(зеленая кривая) и ее аппроксимация (красная кривая) как функция значения отражательной способности

R 1 R 2 {\ displaystyle R_ {1} R_ { 2}}

{\ displaystyle R_ {1} R_ {2}}

. Точные решения ширины линии и изящества Эйри (зеленые линии) правильно разбиваются на

Δ ν A iry = Δ ν FSR {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm { FSR}}}

{\ Displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}}}

, эквивалент

FA iry = 1 {\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 1}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 1}

, тогда как их приближения (красные линии) неправильно не нарушаются. Вставки: Регион

R 1 R 2 < 0.1 {\displaystyle R_{1}R_{2}<0.1}

{\ disp Laystyle R_ {1} R_ {2} <0,1}

Физический смысл лоренцевой утонченности

F c {\ displaystyle {\ mathcal {F}} _ {c}}

{\ Displaystyle {\ math cal {F}} _ {c}}

Fabry- Резонатор Перо. Отображается ситуация для

R 1 = R 2 ≈ 4,32% {\ displaystyle R_ {1} = R_ {2} \ приблизительно 4,32 \%}

{\ displaystyle R_ {1} = R_ {2} \ приблизительно 4,32 \%}

, при котором

Δ ν с = Δ ν FSR {\ Displaystyle \ Delta \ nu _ {c} = \ Delta \ nu _ {\ rm {FSR}}}

{\ displaystyle \ Delta \ nu _ {c} = \ Delta \ nu _ {\ rm {FSR}}}

F c = 1 {\ displaystyle {\ mathcal {F}} _ {c} = 1}

{\ displaystyle {\ mathcal {F}} _ {c} = 1}

, т. е. две соседние лоренцевы линии (пунктирные цветные линии, только 5 линий показаны для ясности для каждой резонансной частоты,

ν q {\ displaystyle \ nu _ {q}}

{\ displaystyle \ nu _ {q}}

) пересекаются на сторону максимума (сплошная черная линия) и критерий Тейлора для спектрального разрешения двух пиков в результирующем разрешении распределения Эйри (сплошная фиолетовая линия, сумма 5 l

Основные лоренцев линии могут быть, пока соблюдается критерий Тейлора (см. рисунок «Физический смысл лоренцевой утонченности»). лоренцев изящество резонатора Фабри-Перо:

F c = Δ ν FSR Δ ν c = 2 π - ln ⁡ (R 1 R 2). {\ Displaystyle {\ mathcal {F}} _ {c} = {\ frac {\ Delta \ nu _ {\ rm {FSR}}} {\ Delta \ nu _ {c}}} = {\ frac {2 \ pi} {- \ ln (R_ {1} R_ {2})}}.}

{\ displaystyle {\ mathcal {F}} _ {c} = {\ frac {\ Delta \ nu _ {\ rm {FSR}}} {\ Delta \ nu _ {c}}} = {\ frac {2 \ pi} {- \ ln (R_ {1} R_ {2})}}.}

Он отображается как синяя линия на рисунке «Физический смысл лоренцевой ловкости». Лоренцевское изящество $F c {\ displaystyle {\ mathcal {F}} _ {c}}$ ${\ Displaystyle {\ math cal {F}} _ {c}}$ имеет фундаментальный физический смысл: оно качества, нас колько хорошо лоренцевы линии, лежащие в основе распределения Эйри, могут быть разрешены, когда измерения Эйри. В точке, где

Δ ν c = Δ ν FSR ⇒ R 1 R 2 = e - 2 π ≈ 0,001867, {\ displaystyle \ Delta \ nu _ {c} = \ Delta \ nu _ {\ rm { FSR}} \ Rightarrow R_ {1} R_ {2} = e ^ {- 2 \ pi} \ приблизительно 0,001867,}

{\ displaystyle \ Delta \ nu _ {c} = \ Delta \ nu _ {\ rm {FSR}} \ Rightarrow R_ {1} R_ {2} = e ^ {- 2 \ pi } \ приблизительно 0,001867,}

эквивалент $F c = 1 {\ displaystyle {\ mathcal {F}} _ {c} = 1}$ ${\ displaystyle {\ mathcal {F}} _ {c} = 1}$ , достигается критерий Тейлора для спектрального разрешения одного распределения Эйри. В этой точке $F c < 1 {\displaystyle {\mathcal {F}}_{c}<1}$ ${\ displaystyle {\ mathcal {F}} _ {c} <1}$ две спектральные линии нельзя различить. Для равных зеркальных отражений эта точка возникает, когда $R 1 = R 2 ≈ 4,32% {\ displaystyle R_ {1} = R_ {2} \ приблизительно 4,32 \%}$ ${\ displaystyle R_ {1} = R_ {2} \ приблизительно 4,32 \%}$ . Следовательно, ширина линии лоренцевых линий, лежащих в основе распределения Эйри-Перо, может быть определена путем определения распределения Эйри, следовательно, его потери в этом резонаторе могут быть спектроскопически до точки.

Сканирование резонатора Фабри-Перо: ширина линии Эйри и изящество

Физический смысл утонченности Эйри

FA iry {\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}}}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Эйри}}}

резонатора Фабри-Перо. При сканировании длины Фабри-Перо (или угла падающего света) распределения Эйри (цветные сплошные линии) следовать сигнала на отдельных частотах. Экспериментальный результат измерения представляет собой сумму индивидуальных распределений Эйри (черная пунктирная линия). Если сигналы возникают на частотах

ν m = ν q + m Δ ν A iry {\ displaystyle \ nu _ {m} = \ nu _ {q} + m \ Delta \ nu _ {\ rm {Airy}}}

{\ displaystyle \ nu _ {m} = \ nu _ {q} + m \ Delta \ nu _ {\ rm {Airy}}}

, где

m {\ displaystyle m}

m

- целое число, начинающееся с

q {\ displaystyle q}

q

, распределения Эйри в соседних частотах отделены друг от друга шириной линии

Δ ν A iry {\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}

{\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}

, тем самым выполняя критерий Тейлора для спектроскопического разрешения двух соседних вершин. Максимальное количество сигналов, которые могут быть разрешены, составляет

F A i r y {\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}}}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Эйри}}}

. В этом конкретном примере коэффициенты отражения

R 1 = R 2 = 0,59928 {\ displaystyle R_ {1} = R_ {2} = 0,59928}

{\ displaystyle R_ {1} = R_ {2} = 0,59928}

были выбраны таким образом, что

FA iry = 6 {\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 6}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 6}

- целое число, сигнал для

m = FA iry {\ displaystyle m = { \ mathcal {F}} _ {\ rm {Эйри}}}

{\ displaystyle m = {\ mathcal {F}} _ {\ rm {Эйри}}}

на частотах

ν q + FA iry Δ ν A iry = ν q + Δ ν FSR {\ displaystyle \ nu _ {q } + {\ mathcal {F}} _ {\ rm {Эйри}} \ Delta \ nu _ {\ rm {Airy}} = \ nu _ {q} + \ Delta \ nu _ {\ rm {FSR}}}

{\ displaystyle \ nu _ {q} + {\ mathcal {F}} _ {\ rm {Эйри}} \ Delta \ nu _ {\ rm {Airy}} = \ nu _ {q} + \ Delta \ nu _ {\ rm {FSR}}}

совпадает с сигналом для

m = q {\ displaystyle m = q}

{\ Displaystyle м = д}

ν q {\ displaystyle \ nu _ {q}}

{\ displaystyle \ nu _ {q}}

. В этом примере максимума

FA iry = 6 {\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 6}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 6}

пиков может быть разрешено при применении критерия Тейлора..

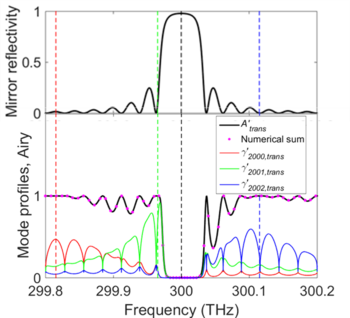
Пример резонатора Фабри-Перо с частотно-зависимой отражательной способностью зеркала (вверху) и полученными профилями искаженных мод (внизу)

γ q, trans '{\ displaystyle \ gamma _ {q, {\ rm {trans}} } ^ {\ prime}}

{\ displaystyle \ gamma _ {q, {\ rm {trans}}} ^ {\ prime}}

режимов с индексами

q = 2000, 2001, 2002 {\ displaystyle q = 2000,2001,2002}

{\ displaystyle q = 2000,2001,2002}

, сумма 6 миллионов профилей мод ( розовые точки, самые разные для нескольких частот) и распределение Эйри

Транс '{\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}

{\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}

. Вертикальные пунктирные линии обозначают максимум кривой отражательной способности (черные) и резонансные частоты отдельных мод (цветные).

Когда резонатор Фабри-Перо используется в качестве сканирующего интерферометра, т. Е. При переменном длине резонатора (или угол падения) можно спектрально спектрально спектральные линии на разных частотах в пределах одного свободного спектрального диапазона диапазона. Несколько распределений Эйри $Транс '(ν) {\ displaystyle A _ {\ rm {trans}} ^ {\ prime} (\ nu)}$ ${\ displaystyle A _ {\ rm {trans}} ^ {\ prime} (\ nu)}$ , каждый из которых создается отдельной спектральной линией, которые должны быть решенным. Следовательно, размер Эйри определяет функцию, и измерение дает сумму распределений Эйри. Параметры, которые правильно определяют эту ситуацию, - это ширина линии Эйри $Δ ν A iry {\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ ${\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ и тонкость Airy $FA iry {\ Displaystyle {\ mathcal {F}} _ {\ rm {Эйри}}}$ ${\ displaystyle {\ mathcal {F}} _ {\ rm {Эйри}}}$ . Ширина линии на FWHM $Δ ν A iry {\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ ${\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ распределения Эйри $A trans '(ν) {\ displaystyle A_ {\ rm {trans}} ^ {\ prime} (\ nu)}$ ${\ displaystyle A _ {\ rm {trans}} ^ {\ prime} (\ nu)}$ is

Δ ν A iry = Δ ν FSR 2 π arcsin ⁡ (1 - R 1 R 2 2 R 1 R 2 4). {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}} {\ frac {2} {\ pi}} \ arcsin \ left ({\ frac {1- {\ sqrt {R_ {1} R_ {2}}}} {2 {\ sqrt [{4}] {R_ {1} R_ {2}}}}} \ right).}

{\ displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}} {\ frac {2} {\ pi}} \ arcsin \ left ({\ frac {1 - {\ sqrt {R_ {1} R_ {2}}}} {2 {\ sqrt [{4} ] {R_ {1} R_ {2}}}}} \ right).}

Ширина линии Эйри $Δ ν Ири {\ displaystyle \ Delta \ nu _ {\ rm {Эйри}}}$ ${\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ отображается как зеленая кривая на рисунке «Лоренцевская ширина линии и изящество в сравнении с шириной линии Эйри и изяществом Фабри. -Резонатор Перо ».

Концепция определения ширины линии пиков Эйри нарушении полуширины на $Δ ν A iry = Δ ν FSR {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}}}$ ${\ Displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}}}$ (сплошная красная линия на рисунке "Распределение Эйри $A транс '{\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ ${\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ "), потому что в этот момент ширина линии Эйри мгновенно перескакивает бесконечное значение для функций $arcsin {\ displaystyle \ arcsin}$ ${\ displaystyle \ arcsin}$ . Для более низких значений отражательной способности $R 1 R 2 {\ displaystyle R_ {1} R_ {2}}$ ${\ displaystyle R_ {1} R_ {2}}$ ширина линии пиков Эйри на FWHM не определена. Предельный случай имеет место при

Δ ν A i r y = Δ ν F S R ⇒ 1 - R 1 R 2 2 R 1 R 2 4 = 1 ⇒ R 1 R 2 ≈ 0,02944. {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}} \ Rightarrow {\ frac {1 - {\ sqrt {R_ {1} R_ {2}}} } {2 {\ sqrt [{4}] {R_ {1} R_ {2}}}}} = 1 \ Rightarrow R_ {1} R_ {2} \ приблизительно 0,02944.}

{\ displaystyle \ Delta \ nu _ {\ rm {Эйри}} = \ Delta \ nu _ {\ rm {FSR}} \ Rightarrow {\ frac {1 - {\ sqrt {R_ {1} R_ {2}}}} {2 {\ sqrt [{4} ] {R_ {1} R_ {2}}}}} = 1 \ Rightarrow R_ {1} R_ {2} \ приблизительно 0,02944.}

Для равных коэффициентов отражения зеркала это точка достигается, когда $R 1 = R 2 ≈ 17,2% {\ displaystyle R_ {1} = R_ {2} \ приблизительно 17,2 \%}$ ${\ displaystyle R_ {1} = R_ {2} \ приблизительно 17,2 \%}$ (сплошная красная линия на рисунок «Распределение Эйри $А транс '{\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ ${\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ ").

Изящество распределения Эри резонатора Фабри-Перо, которое отображается как зеленая кривая на рисунке «Лоренцевская ширина линии и изящество в зависимости от ширины линии Эри и изящества резонатора Фабри-Перо» в прямом сравнении с лоренцевское изящество $F c {\ displaystyle {\ mathcal {F}} _ { c}}$ ${\ Displaystyle {\ math cal {F}} _ {c}}$ определяется как

FA iry = Δ ν FSR Δ ν A iry = π 2 [arcsin ⁡ (1 - R 1 R 2 2 R 1 R 2 4)] - 1. {\ displaystyle {\ mathcal {F}} _ {\ rm {Эйри}} = {\ frac {\ Delta \ nu _ {\ rm {FSR}}} {\ Delta \ nu _ {\ rm {Эйри}}}} = {\ frac {\ pi} {2}} \ left [\ arcsin \ left ({ \ frac {1 - {\ sqrt {R_ {1} R_ {2}}}}} {2 {\ sqrt [{4}] {R_ {1} R_ {2}}}}} \ right) \ right] ^ {- 1}.}

{\ displaystyle {\ mathcal {F}} _ {\ rm {Эйри}} = {\ frac {\ Delta \ nu _ {\ rm {FSR}}} {\ Delta \ nu _ {\ rm {Эйри}}}} = {\ frac {\ pi} {2}} \ left [\ arcsin \ left ({\ frac {1 - {\ sqrt { R_ {1} R_ {2}}}}} {2 {\ sqrt [{4}] {R_ {1} R_ {2}}}}} \ right) \ right] ^ {- 1}.}

При сканировании длины резонатора Фабри-Перо (или угла падающего света), тонкость Эйри количественно определяет максимальное количество распределений Эйри, создаваемых светом на отдельных частотах $ν m {\ displaystyle \ nu _ { m}}$ ${\ displaystyle \ nu _ {m}}$ в свободном спектральном диапазоне резонатора Фабри-Перо, чей соседние пики можно однозначно различить спектроскопически, то есть они не перекрываются на его FWHM (см. рисунок «Физический смысл тонкости Эйри»). Это определение тонкости Эйри согласуется с критерием Тейлора разрешающей способности спектрометра. Концепция ширины линии на полувысоте нарушается при $Δ ν A iry = Δ ν FSR {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}}}$ ${\ Displaystyle \ Delta \ nu _ {\ rm {Airy}} = \ Delta \ nu _ {\ rm {FSR}}}$ , следовательно, тонкость Эйри определяется только до $FA iry = 1 {\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 1}$ ${\ displaystyle {\ mathcal {F}} _ {\ rm {Airy}} = 1}$ , см. рисунок «Лоренцевская ширина линии и точность в зависимости от ширины линии Эри и точность резонатора Фабри-Перо».

Часто ненужное приближение $sin ⁡ (ϕ) ≈ ϕ {\ displaystyle \ sin {(\ phi)} \ приблизительно \ phi}$ ${\ displaystyle \ sin {(\ phi)} \ приблизительно \ phi}$ выполнено при выводе из $Транс ' {\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ ${\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ ширина линии Эйри $Δ ν A iry {\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ ${\ displaystyle \ Delta \ nu _ {\ rm {Airy}}}$ . В отличие от точного решения, приведенного выше, это приводит к

Δ ν A iry ≈ Δ ν FSR 1 π 1 - R 1 R 2 R 1 R 2 4 ⇒ FA iry = Δ ν FSR Δ ν A iry ≈ π R 1 К 2 4 1 - К 1 К 2. {\ displaystyle \ Delta \ nu _ {\ rm {Airy}} \ приблизительно \ Delta \ nu _ {\ rm {FSR}} {\ frac {1} {\ pi} } {\ frac {1 - {\ sqrt {R_ {1} R_ {2}}}} {\ sqrt [{4}] {R_ {1} R_ {2}}}} \ Rightarrow {\ mathcal {F} } _ {\ rm {Эйри}} = {\ frac {\ Delta \ nu _ {\ rm {FSR}}} {\ Delta \ nu _ {\ rm {Эйри}}}} \ приблизительно \ pi {\ frac { \ sqrt [{4}] {R_ {1} R_ {2}}} {1 - {\ sqrt {R_ {1} R_ {2}}}}}.}

{\ displaystyle \ Delta \ nu _ {\ rm {Airy}} \ приблизительно \ Delta \ nu _ {\ rm {FSR }} {\ frac {1} {\ pi}} {\ frac {1 - {\ sqrt {R_ {1} R_ {2}}}} {\ sqrt [{4}] {R_ {1} R_ {2 }}}} \ Rightarrow {\ mathcal {F}} _ {\ rm {Эйри}} = {\ frac {\ Delta \ nu _ {\ rm {FSR}}} {\ Delta \ nu _ {\ rm {Эйри }}}} \ приблизительно \ pi {\ frac {\ sqrt [{4}] {R_ {1} R_ {2}}} {1 - {\ sqrt {R_ {1} R_ {2}}}}}. }

Это приближение ширины линии Эйри, отображенное красным кривой на рисунке "Лоренцевская ширина линии и Изящество по сравнению с шириной линии Эйри и изяществом резонатора Фабри-Перо" отклоняется от правильной кривой при низких коэффициентах отражения и неправильно неается, когда $Δ ν A iry>Δ ν FSR {\ displaystyle \ Дельта \ nu _ {\ rm {Эйри}}>\ Delta \ nu _ {\ rm {FSR}}}$ $\Delta \nu _{\rm {Airy}}>\ Delta \ nu _ {\ rm {FSR}}$ . Это приближение обычно также используется для расчета тонкости Эйри.

Зависимые от частот коэффициенты отражения зеркал

Более общий случай резонатора Фабри-Перо с частотно-зависимыми коэффициентами отражения зеркал можно рассматривать с помощью тех же уравнений, что и выше, за исключением того, что время распада фотона $τ c (ν) {\ displaystyle \ tau _ {c} (\ nu)}$ ${\ displaystyle \ tau _ {c} (\ nu)}$ и ширина линии $Δ ν c (ν) {\ displaystyle \ Delta \ nu _ {c} (\ nu)}$ ${\ displaystyle \ Delta \ nu _ {c} (\ nu)}$ теперь становятся локальными функциями частоты. Ширина линии теряет свое значение, потому что она напоминает спектральную ширину полосы, значение которой теперь изменяется в пределах этой самой полосы. Также в этом случае финансирования Эйри представляет собой сумму всех основных профилей мод, которые могут быть сильно искажены. Пример распределения Эйри $A транс '{\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ ${\ displaystyle A _ {\ rm {trans}} ^ {\ prime}}$ и нескольких профилей основных мод $γ q, trans' (Ν) { \ displaystyle \ gamma _ {q, {\ rm {trans}}} ^ {\ prime} (\ nu)}$ ${\ displaystyle \ gamma _ {q, {\ rm {trans}}} ^ {\ prime} (\ nu)}$ приведен на рисунке «Пример резонатора Фабри-Перо с частотно-зависимой отражательной способностью зеркала».

Резонатор Фабри-Перо с собственными оптическими потерями

Собственные потери при распространении внутри резонатора могут быть количественно оценены с помощью коэффициента потерь интенсивности $α потерь {\ displaystyle \ alpha _ {\ rm { }}}$ ${\ displaystyle \ alpha _ {\ rm { потеря}}}$ на единицу самой потери или потери длины, что то же самое внутреннее при передаче туда и обратно $LRT, {\ displaystyle L _ {\ rm {RT}},}$ ${\ displaystyle L _ {\ rm {RT}},}$ такие, что

1 - LRT = e - α потеря 2 ℓ = e - t RT / τ потеря. {\ Displaystyle 1-L _ {\ rm {RT}} = e ^ {- \ alpha _ {\ rm {loss}} 2 \ ell} = e ^ {- t _ {\ rm {RT}} / \ tau _ {\ rm {loss}}.}

{\ Displaystyle 1-L _ {\ rm {RT}} = е ^ {- \ альфа _ {\ rm {loss}} 2 \ ell} = e ^ {- t _ {\ rm {RT}} / \ tau _ {\ rm {loss}}}.}

Дополнительные потери сокращают время распада фотона $τ c {\ displaystyle \ tau _ {c}}$ $\ tau_c$ резонатора:

1 τ c = 1 τ вых + 1 τ потеря = - ln ⁡ [R 1 R 2 (1 - LRT)] t RT = - ln ⁡ [R 1 R 2] t RT + c α потеря. {\ displaystyle {\ frac {1} {\ tau _ {c}}} = {\ frac {1} {\ tau _ {\ rm {out}}}} + {\ frac {1} {\ tau _ { \ rm {loss}}}} = {\ frac {- \ ln {[R_ {1} R_ {2} (1-L _ {\ rm {RT}})]}} {t _ {\ rm {RT }}}} = {\ frac {- \ ln {[R_ {1} R_ {2}]}} {t _ {\ rm {RT}}}} + c \ alpha _ {\ rm {loss}}. }

{\ displaystyle {\ frac {1} {\ tau _ {c}}} = {\ frac {1} {\ tau _ {\ rm {out}}}} + {\ frac {1} {\ tau _ { \ rm {loss}}}} = {\ frac {- \ ln {[R_ {1} R_ {2} (1-L _ {\ rm {RT}})]}} {t _ {\ rm {RT }}}} = {\ frac {- \ ln {[R_ {1} R_ {2}]}} {t _ {\ rm {RT}}}} + c \ alpha _ {\ rm {loss}}. }

где $c {\ displaystyle c}$ $c$ - скорость света в полости. Общее распределение Эйри или коэффициент усиления внутреннего резонанса $A circ {\ displaystyle A _ {\ rm {circ}}}$ ${\ displaystyle A _ {\ rm {circ}}}$ затем выводится, как указано выше, путем включения потерь на распространение через коэффициент амплитудных потерь $α потеря / 2 {\ displaystyle \ alpha _ {\ rm {loss}} / 2}$ ${\ displaystyle \ alpha _ {\ rm {потеря}} / 2}$ :

E circ = E laun + ERT = E laun + r 1 r 2 e - (α loss / 2) 2 ℓ e - я 2 ϕ E circ ⇒ E circ E laun = 1 1 - r 1 r 2 e - α потеря ℓ e - i 2 ϕ ⇒ {\ displaystyle E _ {\ rm {circ}} = E _ {\ rm {laun }} + E _ {\ rm {RT}} = E _ {\ rm {laun}} + r_ {1} r_ {2} e ^ {- (\ alpha _ {\ rm {loss}} / 2) 2 \ ell} e ^ {- i2 \ phi} E _ {\ rm {circ}} \ Rightarrow {\ frac {E _ {\ rm {circ}}} {E _ {\ rm {laun}}}} = { \ frac {1} {1 -r_ {1} r_ {2} e ^ {- \ alpha _ {\ rm {loss}} \ ell} e ^ {- i2 \ phi}}} \ Rightarrow}

{\ displaystyle E _ {\ rm {circ}} = E _ {\ rm {laun}} + E _ {\ rm {RT}} = E _ {\ rm {laun} } + r_ {1} r_ {2} e ^ {- (\ alpha _ {\ rm {loss}} / 2) 2 \ ell} e ^ {- i2 \ phi} E _ {\ rm {circ}} \ Стрелка вправо {\ frac {E _ {\ rm {circ}}} {E _ {\ rm {laun}}}} = {\ frac {1} {1-r_ {1} r_ {2} e ^ {- \ альфа _ {\ rm {lo ss}} \ ell} e ^ {- i2 \ phi}}} \ Rightarrow}

Цикл = Я кружок Я запускаю = | E c i r c | 2 | Э л а у н | 2 = 1 | 1 - r 1 r 2 e - α l o s s ℓ e - i 2 ϕ | 2 = 1 (1 - R 1 R 2 e - α l o s s) 2 + 4 R 1 R 2 e - α l o s s ℓ sin 2 ⁡ (ϕ). {\ displaystyle A _ {\ rm {circ}} = {\ frac {I _ {\ rm {circ}}} {I _ {\ rm {laun}}}} = {\ frac {\ left | E _ {\ rm {circ}} \ right | ^ {2}} {\ left | E _ {\ rm {laun}} \ right | ^ {2}}} = {\ frac {1} {\ left | 1-r_ {1} r_ {2} e ^ {- \ alpha _ {\ rm {loss}} \ ell} e ^ {- i2 \ phi} \ right | ^ {2}}} = {\ frac {1} {\ left ({1- {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ {\ rm {loss}} \ ell }} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ {\ rm {loss}} \ ell} \ sin ^ {2} (\ phi)}}.}

{\ displaystyle A _ {\ rm {circ}} = {\ frac {I _ {\ rm {circ}}} {I _ {\ rm { Laun}}}} = {\ frac {\ left | E _ {\ rm {circ}} \ right | ^ {2}} {\ left | E _ {\ rm {laun}} \ right | ^ {2}}} = {\ frac {1} {\ left | 1-r_ {1} r_ {2} e ^ {- \ alpha _ {\ rm {loss}} \ ell} e ^ {- i2 \ phi} \ right | ^ {2}}} = {\ frac {1} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ {\ rm {loss}} \ ell }} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ {\ rm {loss}} \ ell} \ sin ^ {2} (\ phi)}}.}

Получены другие распределения Эйри, как указано выше, с помощью данного распределения. В частности, передаточная функция с потерями становится

A trans ′ = I trans I inc = (1 - R 1) (1 - R 2) e - α loss ℓ A circ = (1 - R 1) (1 - R 2) e - α потеря ℓ (1 - R 1 R 2 e - α потеря ℓ) 2 + 4 R 1 R 2 e - α потеря ℓ sin 2 ⁡ (ϕ). {\ displaystyle A _ {\ text {trans}} ^ {\ prime} = {\ frac {I _ {\ rm {trans}}} {I _ {\ rm {inc}}}} = (1-R_ { 1}) (1-R_ {2}) e ​​^ {- \ alpha _ {\ rm {loss}} \ ell} A _ {\ rm {circ}} = {\ frac {(1-R_ {1 }) (1-R_ {2}) e ​​^ {- \ alpha _ {\ rm {loss}} \ ell}} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}} } e ^ {- \ alpha _ {\ rm {loss}} \ ell}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ { \ rm {loss}} \ ell} \ sin ^ {2} (\ phi)}}.}

{\ displaystyle A _ {\ text {trans}} ^ {\ prime} = {\ frac {I _ {\ rm {trans}}} {I _ {\ rm {inc}}}} = (1-R_ {1}) (1-R_ {2}) e ​​^ {- \ alpha _ {\ rm {loss}} \ ell} A _ {\ rm {circ}} = {\ frac {(1-R_ {1}) (1-R_ {2}) e ^ {- \ alpha _ {\ rm {loss}} \ ell}} {\ left ({1 - {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ {\ rm {loss}} \ ell}} \ right) ^ {2} +4 {\ sqrt {R_ {1} R_ {2}}} e ^ {- \ alpha _ {\ rm {loss}} \ ell} \ sin ^ {2} (\ phi)}}.}

Описание резонатора Фабри-Перо в простран волн

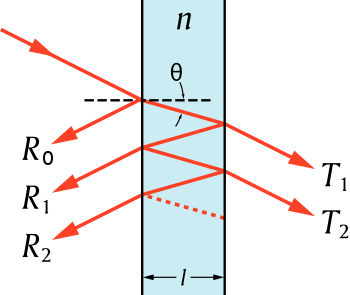
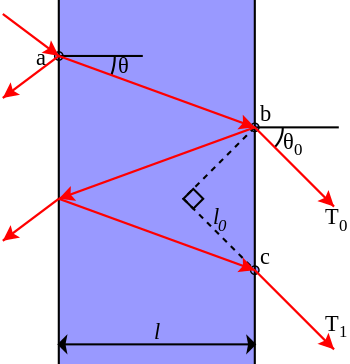
Эталон Фабри-Перо. Свет пронет в эталон и подвергается множественным внутренним отражениям.

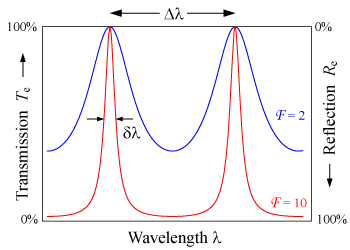
Степень пропускания эталона в зависимости от длины волны. Эталон высокой точности (красная линия) показывает более резкие пики и более низкие минимумы пропускания, чем эталон низкой точности (синий).

Утонченность как функция отражательной способности. Для очень высокой точности требуются зеркала с высокой степенью отражения.

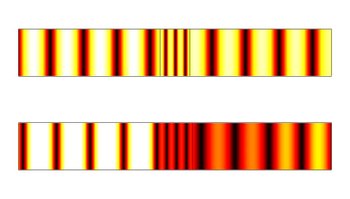
Воспроизвести медиа Анализ переходных процессов кремниевого эталона Фабри - Перо (n = 3,4) при нормальном падении. Верхняя анимация для толщины эталона, выбранная для обеспечения размера пропускания, нижняя анимация - для толщины, выбранной для обеспечения минимального пропускания.

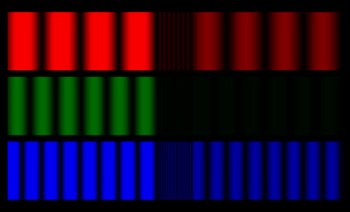
Воспроизвести медиа Переходный процесс ложного цвета для высокого показателя преломления, диэлектрическая плита в воздухе. Толщина / частоты были выбраны таким образом, чтобы красный (вверху) и синий (внизу) передавался максимально, тогда как зеленый (посередине) имел минимальное пропускание.

Различная функция передачи эталона вызывается помехами между множественными отражениями света между двумя отражающими поверхностями. Конструктивная интерференция возникает, если передаваемые лучи находятся в фазе , и это соответствует пику высокой передачи эталона. Если переданные лучи не совпадают, возникают деструктивные помехи, что соответствует минимуму передачи. Находятся ли многократно отраженные лучи в фазе или нет, зависит от длины волны (λ) света (в вакууме), угла, под которым свет проходит через эталон (θ), толщины эталона (ℓ) и показатель преломления материала между отражающими поверхностями (n).

Разность фаз между последовательной другой парой (т.е. T 2 и T 1 на диаграмме) задается как

δ = (2 π λ) 2 n ℓ cos ⁡ θ. {\ displaystyle \ delta = \ left ({\ frac {2 \ pi} {\ lambda}} \ right) 2n \ ell \ cos \ theta.}

{\ displaystyle \ delta = \ left ({\ frac {2 \ pi} {\ lambda}} \ right) 2n \ ell \ cos \ theta.}

Если обе поверхности имеют коэффициент отражения R, функция пропускания эталона определяется как

T e = (1 - R) 2 1-2 R cos ⁡ δ + R 2 = 1 + F sin 2 ⁡ (δ 2), {\ displaystyle T_ {e} = {\ frac {(1-R) ​​^ {2}} {1-2R \ cos \ delta + R ^ {2}}} = {\ frac {1} {1 + F \ sin ^ {2} \ left ({\ frac {\ delta} {2}} \ right)}},}

T_e = \ frac { (1 - R) ^ 2} {1 - 2R \ cos \ delta + R ^ 2} = \ frac {1} {1 + F \ sin ^ 2 \ left (\ frac {\ delta} {2} \ right) },

где

F = 4 R (1 - R) 2 {\ displaystyle F = {\ frac {4R} {(1-R) ​​^ {2}}}}

{\ displaystyle F = {\ frac {4R} {( 1-R) ^ {2}}}}

- коэффициент тонкости.

Максимальная передача ( $T e = 1 {\ displaystyle T_ {e} = 1}$ $T_e = 1$ ) возникает, когда разность длины оптического пути ( $2 nl cos ⁡ θ {\ displaystyle 2nl \ cos \ theta}$ $2 nl \ cos \ тета$ ) между каждым передаваемым лучом является целым числом, кратным длине волны. В отсутствие увеличения коэффициента отражения эталона R e является дополнением к коэффициенту пропускания, так что $T e + R e = 1 {\ displaystyle T_ {e} + R_ {e} = 1}$ $T_e + R_e = 1$ . Максимальный коэффициент отражения равен

R max = 1 - 1 1 + F = 4 R (1 + R) 2, {\ displaystyle R _ {\ max} = 1 - {\ frac {1} {1 + F}} = {\ frac {4R} {(1 + R) ^ {2}}},}

{\ displaystyle R _ {\ max} = 1 - {\ frac {1} {1 + F}} = {\ frac {4R} {(1 + R) ^ {2}}},}

, и это происходит, когда разница в длине пути половины нечетного кратного длины волны.

Разделение длинных волн между соседними пиками пропускания называется свободным спектральным диапазоном (FSR) эталона, Δλ, и определяется как:

Δ λ = λ 0 2 2 нг. ℓ соз ⁡ θ + λ 0 ≈ λ 0 2 2 нг ℓ соз ⁡ θ, {\ displaystyle \ Delta \ lambda = {\ frac {\ lambda _ {0} ^ {2}} {2n _ {\ mathrm {g} } \ ell \ cos \ theta + \ lambda _ {0}}} \ приблизительно {\ frac {\ lambda _ {0} ^ {2}} {2n _ {\ mathrm {g}} \ ell \ cos \ theta} },}

{\ displaystyle \ Delta \ lambda = {\ frac {\ lambda _ {0} ^ {2}} {2n _ {\ mathrm {g}} \ ell \ cos \ theta + \ lambda _ {0}}} \ приблизительно {\ frac {\ lambda _ {0} ^ {2}} {2n _ {\ mathrm {g}} \ ell \ cos \ theta}},}

где λ 0 - центральная длина волны ближайшего пика передачи, а $ng {\ displaystyle n _ {\ mathrm {g}}}$ $n _ {{\ mathrm {g}}}$ - групповой показатель преломления. FSR связан с полушириной на полувысоте, δλ, любой полосой передачи величиной, известной как точность:

F = Δ λ δ λ = π 2 arcsin ⁡ (1 F). {\ displaystyle {\ mathcal {F}} = {\ frac {\ Delta \ lambda} {\ delta \ lambda}} = {\ frac {\ pi} {2 \ arcsin \ left ({\ frac {1} {\ sqrt {F}}} \ right)}}.}

{\ displaystyle {\ mathcal { F}} = {\ frac {\ Delta \ lambda} {\ delta \ lambda}} = {\ гидроразрыв {\ pi} {2 \ arcsin \ left ({\ frac {1} {\ sqrt {F}}} \ справа)}}.}

Обычно это приблизительно (для R>0,5) приблизительно равно

F ≈ π F 2 = π R 1 2 1 - R. {\ displaystyle { \ mathcal {F}} \ приблизительно {\ frac {\ pi {\ sqrt {F}}} {2}} = {\ frac {\ pi R ^ {\ frac {1} {2}}} {1-R }}.}

{\ displaystyle {\ mathcal {F}} \ приблизительно {\ frac {\ pi {\ sqrt {F}}} {2}} = {\ frac {\ pi R ^ {\ frac {1 } {2}}} {1-R}}. }

Если два зеркала не равны, точность становится

F ≈ π (R 1 R 2) 1 4 1 - (R 1 R 2) 1 2. {\ displaystyle {\ mathcal {F}} \ приблизительно {\ frac {\ pi \ left (R_ {1} R_ {2} \ right) ^ {\ frac {1} {4}}} {1- \ left (R_ {1} R_ {2} \ right) ^ {\ frac {1} {2}}}}.}

{\ displaystyle {\ mathcal {F}} \ приблизительно {\ frac { \ pi \ left (R_ {1} R_ {2} \ right) ^ {\ frac {1} {4}}} {1- \ left (R_ {1} R_ {2} \ right) ^ {\ frac { 1} {2}}}}.}

Эталоны с высокой точностью показывают более резкие пики передачи с более низкими минимальными коэффициентами передачи. В случае наклонного падения точности будет зависеть от состояния поляризации луча, поскольку значение R, задаваемое уравнениями Френеля, обычно различается для p- и s-поляризаций.

На изображении показано два луча, один из которых (T 0) передается через эталон, а другой (T 1) перед передачей дважды отражается. При каждом отражении амплитуда уменьшается на $R {\ displaystyle {\ sqrt {R}}}$ $\ sqrt {R}$ , в то время как при каждой передаче через интерфейс амплитуда уменьшается на $T {\ displaystyle {\ sqrt {T}}}$ ${\ sqrt {T}}$ . При наличии силы для сохранения энергии требуется T + R = 1. В приведенном ниже выводе n - показатель преломления внутри эталона, а n 0 - показатель вне эталона. Предполагается, что n>n 0. Амплитуда падающего излучения точка принимает равную единицу, и вектор используются для представления амплитуды излучения. Тогда передаваемая амплитуда в точку b будет

t 0 = T eik ℓ / cos ⁡ θ, {\ displaystyle t_ {0} = T \, e ^ {ik \ ell / \ cos \ theta},}

{\ displaystyle t_ {0} = T \, e ^ {ik \ ell / \ cos \ theta},}

где $k = 2 π n / λ {\ displaystyle k = 2 \ pi n / \ lambda}$ ${\ displaystyle k = 2 \ pi n / \ lambda}$ - волновое число внутри эталона, а λ - длина волны вакуума. В точке c передаваемая амплитуда будет

t 1 ′ = T R e 3 i k ℓ / cos ⁡ θ. {\ displaystyle t '_ {1} = TR \, e ^ {3ik \ ell / \ cos \ theta}.}

t'_{1}=TR\,e^{3ik\ell /\cos \theta }.

Общая амплитуда обоих лучей будет суммой амплитуды двух лучей, измеренных вдоль линии, перпендикулярная область луча. Следовательно, амплитуда t 0 в точке b может быть добавлена к t '1, запаздывающему по фазе на значение $k 0 ℓ 0 {\ displaystyle k_ {0} \ ell _ {0}}$ $k_0 \ ell_0$ , где $k 0 = 2 π n 0 / λ {\ displaystyle k_ {0} = 2 \ pi n_ {0} / \ lambda}$ ${\ displaystyle k_ {0} = 2 \ pi n_ {0} / \ lambda}$ - волновое число вне эталона. Таким образом,

t 1 = TR e (3 ik ℓ / cos ⁡ θ) - ik 0 ℓ 0, {\ displaystyle t_ {1} = TR \, e ^ {\ left (3ik \ ell / \ cos \ theta \ справа) -ik_ {0} \ ell _ {0}},}

{\ displaystyle t_ {1} = TR \, e ^ {\ left (3ik \ ell / \ cos \ theta \ right) -ik_ {0} \ ell _ {0}},}

где ℓ 0 равно

ℓ 0 = 2 ℓ tan ⁡ θ sin ⁡ θ 0. {\ displaystyle \ ell _ {0} = 2 \ ell \ tan \ theta \ sin \ theta _ {0}.}

{ \ displaystyle \ ell _ {0} = 2 \ ell \ tan \ theta \ sin \ theta _ {0}.}

Разность фаз между двумя лучами составляет

δ = 2 k ℓ cos ⁡ θ - к 0 ℓ 0. {\ displaystyle \ delta = {2k \ ell \ over \ cos \ theta} -k_ {0} \ ell _ {0}.}

{\ displaystyle \ delta = {2k \ ell \ over \ cos \ theta} -k_ {0} \ ell _ {0}.}

Связь между θ и θ 0 определяется как закон Снеллиуса :

n грех ⁡ θ = n 0 грех ⁡ θ 0, {\ displaystyle n \ sin \ theta = n_ {0} \ sin \ theta _ {0},}

{\ displaystyle n \ sin \ theta = n_ {0} \ sin \ theta _ {0},}

так, чтобы разность фаз можно записать как

δ = 2 k ℓ cos ⁡ θ. {\ displaystyle \ delta = 2k \ ell \, \ cos \ theta.}

{\ displaystyl e \ delta = 2k \ ell \, \ cos \ theta.}

с точностью до постоянного мультипликативного фазового множителя амплитуды m-го переданного луча можно записать как

t m = T R m e i m δ. {\ displaystyle t_ {m} = TR ^ {m} e ^ {im \ delta}.}

{\ displaystyle t_ {m} = TR ^ {m} e ^ {im \ delta}.}

Полная передаваемая амплитуда - это сумма амплитуд всех отдельных лучей:

t = ∑ m = 0 ∞ tm = T ∑ m = 0 ∞ R meim δ. {\ displaystyle t = \ sum _ {m = 0} ^ {\ infty} t_ {m} = T \ sum _ {m = 0} ^ {\ infty} R ^ {m} \, e ^ {im \ delta }.}

{\ displaystyle t = \ sum _ {m = 0} ^ {\ infty} t_ {m} = T \ sum _ {m = 0} ^ {\ infty} R ^ {m} \, e ^ {im \ delta}.}

Ряд представляет собой геометрический ряд, сумма которого может быть выражена аналитически. Амп амплитуду можно переписать как

t = T 1 - R e i δ. {\ displaystyle t = {\ frac {T} {1-Re ^ {i \ delta}}}.}

{\ displaystyle t = {\ frac {T} {1-Re ^ {i \ delta}}}.}

Интенсивность луча будет в t раз больше его комплексно-сопряженного. Это также даст возможность пропускания:

T e = t t ∗ = T 2 1 + R 2 - 2 R cos ⁡ δ. {\ displaystyle T_ {e} = tt ^ {*} = {\ frac {T ^ {2}} {1 + R ^ {2} -2R \ cos \ delta}}.}

{\ displaystyle T_ {e} = tt ^ {*} = {\ frac {T ^ {2}} {1 + R ^ {2} -2R \ cos \ delta}}.}

Для асимметричной полости то есть одно с двумя разными зеркалами, общая форма передаточной функции:

T e = T 1 T 2 1 + R 1 R 2 - 2 R 1 R 2 cos ⁡ δ. {\ displaystyle T_ {e} = {\ frac {T_ {1} T_ {2}} {1 + R_ {1} R_ {2} -2 {\ sqrt {R_ {1} R_ {2}}} \ cos \ delta}}.}

{\ displaystyle T_ {e} = {\ frac {T_ {1} T_ {2} } {1 + R_ {1} R_ {2} -2 {\ sqrt {R_ {1} R_ {2}}} \ cos \ delta}}.}

Интерферометр Фабри - Перо отличается от эталона Фабри - Перо тем, что расстояние ℓ между пластинами можно настроить, чтобы увеличить длину волн, на которые возникают пики пропускания в интерферометре. Из-за угловой зависимости пропускания пики также могут быть смещены путем поворота эталона относительно луча.

Другое выражение для функций передачи уже было получено в описании в частотном пространстве как бесконечная сумма всех профилей продольных мод. Определение $γ = ln ⁡ (1 R) {\ displaystyle \ gamma = \ ln \ left ({\ frac {1} {R}} \ right)}$ $\ gamma = \ ln \ left (\ frac {1} {R} \ right)$ вышеуказанное выражение может быть записано как

Т е = Т 2 1 - R2 (sh ⁡ γ ch ⁡ γ - cos ⁡ δ). {\ displaystyle T_ {e} = {\ frac {T ^ {2}} {1-R ^ {2}}} \ left ({\ frac {\ sinh \ gamma} {\ cosh \ gamma - \ cos \ delta))}} \ right).}

{\ displaystyle T_ {e} = {\ frac {T ^ {2}} {1-R ^ {2}}} \ left ({\ frac {\ sinh \ гамма} {\ cos \ gamma - \ cos \ delta}} \ right).}

Второй член пропорционален свернутому лоренцевскому распределению, так что передаточная функция может быть записана как серия лоренцевых функций :

T e = 2 π T 2 1 - р 2 ∑ ℓ знак равно - ∞ ∞ L (δ - 2 π ℓ; γ), {\ displaystyle T_ {e} = {\ frac {2 \ pi \, T ^ {2}} {1- R ^ {2 }}} \, \ sum _ {\ ell = - \ infty} ^ {\ infty} L (\ delta -2 \ pi \ ell; \ gamma),}

{\ displaystyle T_ {e} = {\ frac {2 \ pi \, T ^ {2}} {1-R ^ {2}}} \, \ sum _ {\ ell = - \ infty} ^ {\ infty} L (\ delta -2 \ pi \ ell; \ gamma),}

где

L (x; γ) = γ π (x 2 + γ 2). {\ displaystyle L (x; \ gamma) = {\ frac {\ gamma} {\ pi \ left (x ^ {2} + \ gamma ^ {2} \ right)}}.}

{\ dis стиль игры L (x; \ gamma) = {\ frac {\ gamma} {\ pi \ left (х ^ {2} + \ гамма ^ {2} \ right)}}.}

См. также

Примечания

Ссылки

Эрнандес, Г. (1986). Интерферометры Фабри - Перо. Кембридж: Cambridge University Press. ISBN 0-521-32238-3.

Внешние ссылки

Advanced Design of Etalons - от Precision Photonics Corporation