 . Пятиугольный купол (пример) . Пятиугольный купол (пример) | |
| Символ Шлефли | {n} || t {n} |
| Грани | n треугольники,. n квадраты,. 1 n-угольник,. 1 2n-угольник |
| Edge | 5n |
| Vertices | 3n |
| Группа симметрии | Cnv, [1, n], (* nn), порядок 2n |
| Группа вращения | Cn, [1, n], (nn), порядок n |
| Двойные | ? |
| Свойства | выпуклый |
В геометрии, купол представляет собой твердое тело, образованное соединением двух многоугольников, один ( основание) с вдвое большим количеством ребер, чем у другого, чередующейся полосой равнобедренных треугольников и прямоугольников. Если треугольники равносторонние , а прямоугольники квадраты, а основание и противоположная грань - правильные многоугольники, треугольник, квадрат и пятиугольник купола - все они входят в число тел Джонсона и могут быть образованы путем взятия сечений кубооктаэдра, ромбокубооктаэдра и ромбикосододекаэдр соответственно.
Купол можно рассматривать как призму, где один из многоугольников свернут пополам путем слияния альтернативных вершин.
Куполу можно присвоить удлиненный символ Шлефли {n} || t {n}, представляющий правильный многоугольник {n}, соединенный параллелью его усечения, t {n} или {2n}.
Купола являются подклассом призматоидов.
Его двойник содержит форму, которая является своего рода сварным швом между половиной n-стороннего трапецоэдра и 2n-сторонним пирамида.
| n | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Имя | {2} || t {2} | {3} || t {3} | {4} || t {4} | {5} || t {5} | {6} || t {6} |
| Купол |  . Двухугольный купол . Двухугольный купол |  . Треугольный купол . Треугольный купол |  . Квадратный купол . Квадратный купол |  . Пятиугольный купол . Пятиугольный купол |  .. (Плоский) .. (Плоский) |
| Связанные. однородные. многогранники | Треугольная призма. | Кубоокта-. эдр. | Ромби-. кубокта-. эдр. | Ромб-. икосидодека-. эдр. | Ромби-. трехгексагональный. мозаика. |
 Плоскость «шестиугольник купола» в ромбитрихексагональной мозаике
Плоскость «шестиугольник купола» в ромбитрихексагональной мозаике Вышеупомянутые три многогранника являются единственными нетривиальными выпуклыми куполами с правильными гранями: "шестиугольный купол »- это плоская фигура, а треугольная призма может считаться« куполом »степени 2 (купол линейного сегмента и квадрата). Однако купола многоугольников более высокой степени могут быть построены с неправильными треугольными и прямоугольными гранями.
 40-гранный купол имеет 40 равнобедренных треугольников (синие), 40 прямоугольников (желтые), верхний правильный 40-угольник (красный) и нижний. обычный 80-угольник (скрытый).
40-гранный купол имеет 40 равнобедренных треугольников (синие), 40 прямоугольников (желтые), верхний правильный 40-угольник (красный) и нижний. обычный 80-угольник (скрытый). Определение купола не требует, чтобы основание (или сторона, противоположная основанию, которую можно назвать вершиной), было правильным многоугольником, но Удобно рассмотреть случай, когда купол имеет максимальную симметрию, C nv. В этом случае вершина представляет собой правильный n-угольник, а основание - это либо правильный 2n-угольник, либо 2n-угольник, у которого чередуются две разные длины сторон и те же углы, что и у правильного 2n-угольника. Систему координат удобно зафиксировать так, чтобы основание лежало в плоскости xy, а верх - в плоскости, параллельной плоскости xy. Ось z - это ось n-го сгиба, а плоскости зеркала проходят через ось z и делят пополам стороны основания. Они также либо делят пополам стороны или углы верхнего многоугольника, либо и то, и другое. (Если n четно, половина зеркальных плоскостей делит пополам стороны верхнего многоугольника и половину пополам углы, а если n нечетное, каждая зеркальная плоскость делит пополам одну сторону и один угол верхнего многоугольника.) Вершины основания могут быть обозначены от V 1 до V 2n, а вершины верхнего многоугольника могут быть обозначены от V 2n + 1 до V 3n. С помощью этих соглашений координаты вершин можно записать как:
где j = 1, 2,..., n.
Поскольку многоугольники V 1V2V2n + 2 V 2n + 1 и т. Д. Являются прямоугольниками, это накладывает ограничение на значения r b, r t и α. Расстояние V 1V2равно
, а расстояние V 2n + 1 V 2n + 2 равно
Они должны быть равны, и если это общее ребро обозначено s,
Эти значения должны быть вставлены в выражения для координат вершин, данные ранее.
| н / д | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |  . {4/3} . {4/3} |  . {5/3} . {5/3} |  . {7/3} . {7/3} |  . {8/3} . {8/3} |
| 5 | — | — |  . {7/5} . {7/5} |  . {8/5} . {8/5} |
| ⁄d | 3 | 5 | 7 |
|---|---|---|---|
| 2 |  . Перекрещенный треугольный куплоид . Перекрещенный треугольный куплоид |  . Пентаграмматический куплоид . Пентаграмматический куплоид |  . Гептаграмматический куплоид . Гептаграмматический куплоид |
| 4 | — |  . Перекрещенный пятиугольный куплоид . Перекрещенный пятиугольный куплоид |  . Перекрещенный гептаграмматический куплоид . Перекрещенный гептаграмматический куплоид |
Звездчатые купола существуют для всех оснований {n / d}, где / 5< /d< 6 and d is odd. At the limits the cupolae collapse into plane figures: beyond the limits the triangles and squares can no longer span the distance between the two polygons. When d is even, the bottom base {2n/d} becomes degenerate: we can form a cuploid or semicupola by withdrawing this degenerate face and instead letting the triangles and squares connect to each other here. In particular, the тетрагемигексаэдр может рассматриваться как {3/2} -куплоид. Все купола ориентируемы, а куплоиды все неориентируемы. Когда n / d>2 в куплоиде, треугольники и квадраты не покрывают все основание, и в основании остается небольшая мембрана, которая просто закрывает пустое пространство. Следовательно, куплоиды {5/2} и {7/2}, изображенные выше, имеют мембраны (не заполненные), тогда как куплоиды {5/4} и {7/4}, изображенные выше, не имеют.
Высота h {n / d} -куполки или куплоида определяется по формуле 
На изображениях выше звездным куполам дана согласованная цветовая схема, чтобы помочь идентифицировать их лица: базовый n / d-угольник красный, основание 2n / d-угольник желтый, квадраты синие, треугольники зеленые. У куплоидов основание n / d-угольник красное, квадраты - желтые, а треугольники - синие, так как другое основание было удалено.
 . Пятиугольный пример . Пятиугольный пример | |
| символ Шлефли | s {n} || t {n} |
| Лица | 3n треугольники. 1 n-угольник,. 1 2n-угольник |
| Ребра | 6n |
| Вершины | 3n |
| Группа симметрии | Cnv, [1, n], (* nn), порядок 2n |
| Группа вращения | Cn, [1, n], (nn), порядок n |
| Двойные | ? |
| Свойства | выпуклые |
n-угольная антикупола построена из правильного 2n-угольного основания, 3n треугольников двух типов и правильного n -кональный верх. При n = 2 верхняя грань двуугольника сводится к единственному ребру. Вершины верхнего многоугольника выровнены с вершинами нижнего многоугольника. Симметрия C nv, порядок 2n.
Антикупола не может быть построена со всеми правильными гранями, хотя некоторые могут быть сделаны регулярными. Если верхний n-угольник и треугольники правильные, то основание 2n-угольника не может быть плоским и правильным. В таком случае n = 6 образует правильный шестиугольник и окружающие равносторонние треугольники курносой шестиугольной мозаики, которая может быть замкнута в многоугольник нулевого объема с основанием в виде симметричного 12-угольника, имеющего форму большего шестиугольника., имеющий смежные пары коллинеарных ребер.
Две антикуполы могут быть увеличены вместе на их основе как a.
| n | 2 | 3 | 4 | 5 | 6... |
|---|---|---|---|---|---|
| Имя | s {2} || t {2} | s {3} || t {3} | s {4} || t {4} | s {5} || t {5} | s {6} || t {6} |
| Изображение |  . Дигонал . Дигонал |  . Треугольник . Треугольник |  . Квадрат . Квадрат | 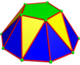 . Пятиугольник . Пятиугольник |  . Шестиугольник . Шестиугольник |
| Прозрачный |  |  |  |  | |
| Сетка |  |
hypercupolae или многогранные купола представляют собой семейство выпуклых неоднородных полихор (здесь четырехмерных фигур), аналогичных куполам. Основание каждого из них - это Платоново твердое тело и его расширение.
| Имя | Тетраэдрический купол | Кубический купол | Восьмигранный купол | Додекаэдрический купол | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Символ Шлефли | {3,3} || rr {3,3} | {4,3} || rr {4,3} | {3,4} || rr {3,4} | {5,3} || rr {5,3} | {6,3} || rr {6,3} | |||||
| Segmentochora. index | K4.23 | K4.71 | K4.107 | K4.152 | ||||||
| радиус окружности | 1 | sqrt ((3 + sqrt (2)) / 2). = 1,485634 | sqrt (2 + sqrt (2)). = 1,847759 | 3 + sqrt (5). = 5.236068 | ||||||
| Изображение |  |  |  |  | ||||||
| Концевые ячейки |   |   |   |   |   | |||||
| Вершины | 16 | 32 | 30 | 80 | ∞ | |||||
| Края | 42 | 84 | 84 | 210 | ∞ | |||||
| Грани | 42 | 24 {3} + 18 {4} | 80 | 32 {3} + 48 {4} | 82 | 40 {3} + 42 {4} | 194 | 80 {3} + 90 {4} + 24 {5} | ∞ | |
| Ячейки | 16 | 1 тетраэдр. 4 треугольные призмы. 6 треугольные призмы. 4 треугольные пирамиды. 1 кубооктаэдр | 28 | 1 куб. 6 квадратные призмы. 12 треугольные призмы. 8 треугольные пирамиды. 1 ромбокубооктаэдр | 28 | 1 октаэдр. 8 треугольные призмы. 12 треугольные призмы. 6 квадратные пирамиды. 1 ромбокубооктаэдр | 64 | 1 додек аэдр. 12 пятиугольных призм. 30 треугольных призм. 20 треугольных пирамид. 1 ромбикосододекаэдр | ∞ | 1 шестиугольная мозаика. ∞ гексагональные призмы. ∞ треугольные призмы. ∞ треугольные пирамиды. 1 ромбитрихексагональная мозаика |
| Связанная. однородная. полихора | 5-ячеечная. | рунцинированная тессеракта. | ранцинированная 24 -ячейка. | многогранник из 120 клеток. | многогранник с гексагональной мозаикой. | |||||