Изменение базиса

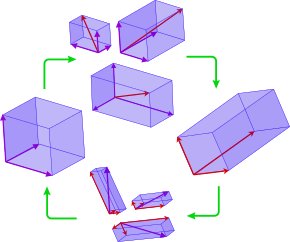
Изменение координат для векторного пространства A линейная комбинация одного базисного набора векторов (фиолетовый) получает новое векторы (красный). Если они линейно независимы, они образуют новый базовый набор. Линейные комбинации, связывающие первый набор с другим, расширяются до линейного преобразования, называемого изменением базиса. Вектор, представленный двумя разными базами (фиолетовая и красная стрелки).

In линейной алгебры, базис для векторного пространства - это линейно независимый набор , охватывающий векторное пространство. В этой статье рассматриваются в основном конечномерные векторные пространства, но многие из теорем справедливы и для бесконечномерных векторных пространств. Базисом векторного пространства размерности n является набор из n векторов (α 1,…, α n), называемых базисными векторами, с тем свойством, что каждый вектор в пространстве может быть выражен как уникальная линейная комбинация базисных векторов. Матричные представления из операторов также определяются выбранным базисом. Поскольку часто желательно работать с более чем одним базисом для векторного пространства, принципиально важно в линейной алгебре иметь возможность легко преобразовывать покоординатные представления векторов и операторов, взятых относительно одного базиса, в их эквивалентные представления с уважение к другому основанию. Такое преобразование называется изменением базиса . Например, если $A\; \in \; R\; n\; \times \; n\; \{\backslash \; displaystyle\; A\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{n\; \backslash \; times\; n\}\}$- это матрица, столбцы которой составляют основу $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\}$, вектор $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$(в стандартном базисе) может также может быть выражено как линейная комбинация столбцов $A\; \{\backslash \; displaystyle\; A\}$вектором $A\; -\; 1\; v\; \{\backslash \; displaystyle\; A\; ^\; \{-\; 1\}\; \backslash \; mathbf\; \{v\}\; \}$. Таким образом, по определению $A\; (A\; -\; 1\; v)\; =\; (AA\; -\; 1)\; v\; =\; v\; \{\backslash \; displaystyle\; A\; (A\; ^\; \{-\; 1\}\; \backslash \; mathbf\; \{v\})\; =\; (AA\; ^\; \{-\; 1\})\; \backslash \; mathbf\; \{v\}\; =\; \backslash \; mathbf\; \{v\}\}$. Если столбцы $A\; \{\backslash \; displaystyle\; A\}$образуют ортонормированный базис, то инверсия $A\; \{\backslash \; displaystyle\; A\}$- это его транспонирование, и у нас есть изменение базы как $AT\; v\; \{\backslash \; displaystyle\; A\; ^\; \{T\}\; \backslash \; mathbf\; \{v\}\}$, то есть вектор $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$Скалярные проекции на столбцы $A\; \{\backslash \; displaystyle\; A\}$.

Хотя символ R, используемый ниже, можно понимать как обозначение поля действительные числа, результаты действительны, если R заменяется любым полем F . Хотя ниже используется терминология векторных пространств, обсуждаемые результаты справедливы, когда R является коммутативным кольцом и векторное пространство везде заменяется на free R -модуль.

• 1 Предварительные сведения
  • 1.1 Матрица преобразований
  • 1.2 Единственность линейных преобразований
    • 1.2.1 Теорема
      • 1.2.1.1 Изоморфизм координат
  • 1.3 Матрица множества векторы
• 2 Изменение координат вектора
  • 2.1 Два измерения
  • 2.2 Три измерения
  • 2.3 Общий случай
• 3 Матрица линейного преобразования
  • 3.1 Изменение базиса
• 4 Матрица эндоморфизма
  • 4.1 Изменение базиса
• 5 Матрица билинейной формы
  • 5.1 Изменение базиса
• 6 Важные примеры
• 7 См. Также
• 8 Примечания
• 9 Ссылки
• 10 Внешние ссылки

Матрица преобразования

Стандартный базис для $R\; n\; \{\backslash \; displaystyle\; R\; ^\; \{n\}\}$- это упорядоченная последовательность $E\; n\; =\; \{e\; 1,\; \cdots ,\; en\}\; \{\backslash \; displaystyle\; E\_\; \{n\}\; =\; \backslash \; \{e\_\; \{1\},\; \backslash \; cdots,\; e\_\; \{n\}\; \backslash \}\}$, где $ej\; \{\backslash \; displaystyle\; e\_\; \{j\}\}$- элемент из $R\; n\; \{\backslash \; displaystyle\; R\; ^\; \{n\}\}$с $1\; \{\backslash \; displaystyle\; 1\}$в $j\; th\; \{\backslash \; displaystyle\; j\; ^\; \{\; \backslash \; text\; \{th\}\}\}$разместить и $0\; \{\backslash \; displaystyle\; 0\}$в другом месте. Например, стандартным основанием для $R\; 2\; \{\backslash \; displaystyle\; R\; ^\; \{2\}\}$будет

$E\; 2\; =\; \{(1\; 0),\; (0\; 1)\}\; \{\backslash \; displaystyle\; E\_\; \{2\}\; =\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{pmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\},\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; \backslash \; right\; \backslash \}\}$

Если $T:\; R\; n\; \to \; R\; m\; \{\backslash \; displaystyle\; T:\; R\; ^\; \{n\}\; \backslash \; rightarrow\; R\; ^\; \{m\}\}$- это линейное преобразование, $m\; \times \; n\; \{\backslash \; displaystyle\; m\; \backslash \; times\; n\}$матрица, связанная с $T\; \{\backslash \; displaystyle\; T\}$, является матрицей $MT\; \{\backslash \; displaystyle\; M\_\; \{T\}\}$, j-й столбец которого равен $T\; (ej)\; \in \; R\; m\; \{\backslash \; displaystyle\; T\; (e\_\; \{j\})\; \backslash \; in\; R\; ^\; \{m\}\}$, для $j\; =\; 1,\; \cdots ,\; n\; \{\backslash \; displaystyle\; j\; =\; 1,\; \backslash \; cdots,\; n\}$, то есть

$MT\; =\; [T\; (e\; 1)\; \cdots \; T\; (ej)\; \cdots \; T\; (en)]\; \in \; R\; м\; \times \; N\; \{\backslash \; Displaystyle\; M\_\; \{T\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; T\; (e\_\; \{1\})\; \backslash \; cdots\; T\; (e\_\; \{j\})\; \backslash \; cdots\; T\; (e\_\; \{n\})\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; in\; R\; ^\; \{m\; \backslash \; times\; n\}\}$

В этом случае мы имеем $T\; (x)\; =\; MT\; \cdot \; x\; \{\backslash \; displaystyle\; T\; (x)\; =\; M\_\; \{T\}\; \backslash \; cdot\; x\}$, $\forall \; x\; \in \; R\; n\; \{\backslash \; displaystyle\; \backslash \; forall\; x\; \backslash \; in\; R\; ^\; \{n\}\}$, где мы рассматриваем $x\; \{\backslash \; displaysty\; le\; x\}$как вектор-столбец, а умножение справа - это матричное умножение. Базовым фактом линейной алгебры является то, что векторное пространство Hom ($R\; n,\; R\; m\; \{\backslash \; displaystyle\; R\; ^\; \{n\},\; R\; ^\; \{m\}\}$) всех линейных преобразований из $R\; n\; \{\backslash \; displaystyle\; R\; ^\; \{n\}\}$to $R\; m\; \{\backslash \; displaystyle\; R\; ^\; \{m\}\}$естественно изоморфен пространство $R\; m\; \times \; n\; \{\backslash \; displaystyle\; R\; ^\; \{m\; \backslash \; times\; n\}\}$из $m\; \times \; n\; \{\backslash \; displaystyle\; m\; \backslash \; times\; n\}$матриц над $R\; \{\backslash \; displaystyle\; R\}$; то есть линейное преобразование $T:\; R\; n\; \to \; R\; m\; \{\backslash \; displaystyle\; T:\; R\; ^\; \{n\}\; \backslash \; rightarrow\; R\; ^\; \{m\}\}$во всех смыслах эквивалентно своей матрице $MT\; \{\backslash \; displaystyle\; M\_\; \{T\}\}$.

Уникальность линейных преобразований

Мы также воспользуемся следующим наблюдением.

Теорема

Пусть $V\; \{\backslash \; displaystyle\; V\}$и $W\; \{\backslash \; displaystyle\; W\}$- векторные пространства, пусть $B\; =\; \{\alpha \; 1,\; \cdots ,\; \alpha \; n\}\; \{\backslash \; displaystyle\; B\; =\; \backslash \; \{\backslash \; alpha\; \_\; \{1\},\; \backslash \; cdots,\; \backslash \; alpha\; \_\; \{n\}\; \backslash \}\}$быть основой для $V\; \{\backslash \; displaystyle\; V\}$, и пусть $C\; =\; \{\gamma \; 1,\; \cdots ,\; \gamma \; n\}\; \{\backslash \; displaystyle\; C\; =\; \backslash \; \{\backslash \; gamma\; \_\; \{1\},\; \backslash \; cdots,\; \backslash \; гамма\; \_\; \{n\}\; \backslash \}\}$- любые $n\; \{\backslash \; displaystyle\; n\}$векторы в $W\; \{\backslash \; displaystyle\; W\}$. Тогда существует уникальное линейное преобразование $T:\; V\; \to \; W\; \{\backslash \; displaystyle\; T:\; V\; \backslash \; rightarrow\; W\}$с $T\; (\alpha \; j)\; =\; \gamma \; j\; \{\backslash \; displaystyle\; T\; (\backslash \; alpha\; \_\; \{j\})\; =\; \backslash \; gamma\; \_\; \{j\}\}$, для $j\; =\; 1,\; \cdots ,\; n\; \{\backslash \; displaystyle\; j\; =\; 1,\; \backslash \; cdots,\; n\}$.

Этот уникальный $T\; \{\backslash \; displaystyle\; T\}$определяется как

$T\; (x\; 1\; \alpha \; 1\; +\; \cdots \; +\; xn\; \alpha \; n)\; =\; T\; (x\; 1\; \alpha \; 1)\; +\; \cdots \; +\; T\; (xn\; \alpha \; n)\; =\; Икс\; 1\; T\; (\alpha \; 1)\; +\; \cdots \; +\; xn\; T\; (\alpha \; N)\; знак\; равно\; x\; 1\; \gamma \; 1\; +\; \cdots \; +\; xn\; \gamma \; N\; \{\backslash \; Displaystyle\; T\; (x\_\; \{1\}\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; alpha\; \_\; \{n\})\; =\; T\; (x\_\; \{1\}\; \backslash \; alpha\; \_\; \{1\})\; +\; \backslash \; cdots\; +\; T\; (x\_\; \{n\}\; \backslash \; alpha\; \_\; \{n\})\; =\; x\_\; \{1\}\; T\; (\backslash \; alpha\; \_\; \{1\; \})\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; T\; (\backslash \; alpha\; \_\; \{n\})\; =\; x\_\; \{1\}\; \backslash \; gamma\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; gamma\; \_\; \{n\}\}$

Конечно, если $C\; =\; \{\gamma \; 1,\; \cdots ,\; \gamma \; n\}\; \{\backslash \; displaystyle\; C\; =\; \backslash \; \{\backslash \; gamma\; \_\; \{1\},\; \backslash \; cdots,\; \backslash \; gamma\; \_\; \{n\}\; \backslash \}\}$происходит с быть основой для $W\; \{\backslash \; displaystyle\; W\}$, тогда $T\; \{\backslash \; displaystyle\; T\}$является биективным, а также линейным; другими словами, $T\; \{\backslash \; displaystyle\; T\}$- это изоморфизм. Если в этом случае у нас также есть $W\; =\; V\; \{\backslash \; displaystyle\; W\; =\; V\}$, то $T\; \{\backslash \; displaystyle\; T\}$называется автоморфизм.

Изоморфизм координат

Теперь пусть $V\; \{\backslash \; displaystyle\; V\}$будет векторным пространством над $R\; \{\backslash \; displaystyle\; R\}$и предположим, что $B\; =\; \{\alpha \; 1,\; \cdots ,\; \alpha \; n\}\; \{\backslash \; displaystyle\; B\; =\; \backslash \; \{\backslash \; alpha\; \_\; \{1\},\; \backslash \; cdots,\; \backslash \; alpha\; \_\; \{n\}\; \backslash \}\}$является основа для $V\; \{\backslash \; displaystyle\; V\}$. По определению, если $\xi \; \{\backslash \; displaystyle\; \backslash \; xi\}$является вектором в $V\; \{\backslash \; displaystyle\; V\}$, то $\xi \; =\; x\; 1\; \alpha \; 1\; +\; \cdots \; +\; xn\; \alpha \; n\; \{\backslash \; displaystyle\; \backslash \; xi\; =\; x\_\; \{1\}\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; alpha\; \_\; \{n\}\}$для уникального выбора скаляры $x\; 1,\; \cdots ,\; xn\; \in \; R\; \{\backslash \; displaystyle\; x\_\; \{1\},\; \backslash \; cdots,\; x\_\; \{n\}\; \backslash \; in\; R\}$, называемые координатами $\xi \; \{\; \backslash \; displaystyle\; \backslash \; xi\}$относительно упорядоченного базиса $B\; \{\backslash \; displaystyle\; B\}$. Вектор $x\; =\; (x\; 1,\; \cdots ,\; xn)\; T\; \in \; R\; n\; \{\backslash \; displaystyle\; x\; =\; (x\_\; \{1\},\; \backslash \; cdots,\; x\_\; \{n\})\; ^\; \{T\}\; \backslash \; in\; R\; ^\; \{n\}\}$называется кортежем координат $\xi \; \{\backslash \; displaystyle\; \backslash \; xi\}$относительно $B\; \{\backslash \; displaystyle\; B\}$.

Уникальная линейная карта $\varphi \; :\; R\; N\; \to \; V\; \{\backslash \; displaystyle\; \backslash \; phi:\; R\; ^\; \{n\}\; \backslash \; rightarrow\; V\}$с $\varphi \; (ej)\; =\; \alpha \; j\; \{\backslash \; displaystyle\; \backslash \; phi\; (e\_\; \{j\})\; =\; \backslash \; alpha\; \_\; \{j\}\}$для $j\; =\; 1,\; \cdots ,\; n\; \{\backslash \; displaystyle\; j\; =\; 1,\; \backslash \; cdots,\; n\}$называется изоморфизмом координат для $V\; \{\backslash \; displaystyle\; V\}$и основы $B\; =\; \{\alpha \; 1,\; \cdots ,\; \alpha \; n\}\; \{\backslash \; displaystyle\; B\; =\; \backslash \; \{\backslash \; alpha\; \_\; \{1\},\; \backslash \; cdots,\; \backslash \; alpha\; \_\; \{n\}\; \backslash \}\}$. Таким образом, $\varphi \; (x)\; =\; \xi \; \{\backslash \; displaystyle\; \backslash \; phi\; (x)\; =\; \backslash \; xi\}$тогда и только тогда, когда $\xi \; =\; x\; 1\; \alpha \; 1\; +\; \cdots \; +\; xn\; \alpha \; n\; \{\backslash \; displaystyle\; \backslash \; xi\; =\; x\_\; \{1\}\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; alpha\; \_\; \{n\}\}$.

Матрица набора векторов

Набор векторов может быть представлен матрицей, каждый столбец которой состоит из компонентов соответствующего вектора множества. Поскольку базис - это набор векторов, то базисом может быть матрица такого типа. Позже будет показано, что с этой матрицей связано изменение основы любого объекта пространства. Например, векторы изменяются вместе с обратными (и поэтому их называют контравариантными объектами).

Сначала рассмотрим вопрос о том, как координаты вектора $\xi \; \{\backslash \; displaystyle\; \backslash \; xi\}$в векторном пространстве $V\; \{\backslash \; displaystyle\; V\}$изменяется, когда мы выбираем другую основу.

Два измерения

Это означает, что для данной матрицы $M\; \{\backslash \; displaystyle\; M\}$, столбцы которой являются векторами нового базиса пространства (новый базис матрица), новые координаты для вектора-столбца $v\; \{\backslash \; displaystyle\; v\}$задаются матричным произведением $M\; -\; 1\; v\; \{\backslash \; displaystyle\; M\; ^\; \{-\; 1\}\; v\}$. По этой причине говорят, что обычные векторы являются контравариантными объектами.

Любой конечный набор векторов может быть представлен матрицей, в которой ее столбцы являются координатами данных векторов. В качестве примера в размерности 2 пара векторов получена поворотом стандартного базиса против часовой стрелки на 45 °. Матрица, столбцы которой являются координатами этих векторов:

$M\; =\; [1\; 2\; -\; 1\; 2\; 1\; 2\; 1\; 2]\; \{\backslash \; displaystyle\; M\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\; \}\}\; \{\backslash \; frac\; \{-1\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; end\; \{bmatrix\}\}\}$

Если мы хотим изменить какой-либо вектор пространства на этот новый базис, нам нужно только умножить его компоненты слева на обратную матрицу.

Трехмерное измерение

Например, пусть R будет новым базисом, заданным его углами Эйлера. Матрица базиса будет иметь в качестве столбцов компоненты каждого вектора. Следовательно, эта матрица будет иметь вид (см. Углы Эйлера статью):

$R\; =\; [c\; \alpha \; c\; \gamma \; -\; s\; \alpha \; c\; \beta \; s\; \gamma \; -\; c\; \alpha \; s\; \gamma \; -\; s\; \alpha \; c\; \beta \; c\; \gamma \; s\; \beta \; s\; \alpha \; s\; \alpha \; c\; \gamma \; +\; c\; \alpha \; c\; \beta \; s\; \gamma \; -\; s\; \alpha \; s\; \gamma \; +\; c\; \alpha \; c\; \beta \; c\; \gamma \; -\; s\; \beta \; c\; \alpha \; s\; \beta \; s\; \gamma \; s\; \beta \; c\; \gamma \; c\; \beta ].\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; gamma\}\; -\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; gamma\}\; -\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; gamma\}\; -\; \backslash \; mathrm\; \{\; s\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; gamma\}\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; alpha\}\; \backslash \backslash \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; gamma\}\; +\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; beta\; \}\; \backslash ,\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; gamma\}\; -\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; gamma\}\; +\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; gamma\}\; -\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; alpha\}\; \backslash \backslash \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; gamma\}\; \backslash \; mathrm\; \{s\}\; \_\; \{\backslash \; beta\}\; \backslash ,\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; gamma\}\; \backslash \; mathrm\; \{c\}\; \_\; \{\backslash \; beta\}\; \backslash \; end\; \{bmatrix\}\}.\}$

Опять же, любой вектор пространства можно заменить на этот новый базис, умножив его компоненты слева на обратную матрицу.

Общий случай

Предположим, $A\; =\; \{\alpha \; 1,\dots ,\; \alpha \; n\}\; \{\backslash \; displaystyle\; A\; =\; \backslash \; \{\backslash \; alpha\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; alpha\; \_\; \{\; n\}\; \backslash \}\}$и $B\; =\; \{\beta \; 1,\dots ,\; \beta \; n\}\; \{\backslash \; displaystyle\; B\; =\; \backslash \; \{\backslash \; beta\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; beta\; \_\; \{n\}\; \backslash \; \}\}$- два упорядоченных базиса для n-мерного векторного пространства V над полем K. Пусть φ A и φ B - соответствующие координатные изоморфизмы (линейные карты ) от K до V, т. Е. $\varphi \; A\; (ei)\; =\; \alpha \; i\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{A\}\; (e\_\; \{i\})\; =\; \backslash \; alpha\; \_\; \{i\}\}$и $\varphi \; B\; (ei)\; =\; \beta \; i\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{B\}\; (e\_\; \{i\})\; =\; \backslash \; beta\; \_\; \{i\}\}$для i = 1, …, N, где e i обозначает набор из n, в котором i элемент равен 1, а все остальные элементы равны 0.

Если $x\; =\; (x\; 1,\dots ,\; xn)\; \{\backslash \; displaystyle\; x\; =\; (x\_\; \{1\},\; \backslash \; dots,\; x\_\; \{n\})\}$- кортеж из n координат вектора v в V относительно базиса A, так что $v\; =\; \varphi \; A\; (x)\; \{\backslash \; displaystyle\; v\; =\; \backslash \; phi\; \_\; \{A\}\; (x)\}$, то кортеж координат v относительно B - это такой кортеж y, что $\varphi \; B\; (y)\; знак\; равно\; v\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{B\}\; (y)\; =\; v\}$, т.е. $y\; =\; \varphi \; B\; -\; 1\; (v)\; =\; \varphi \; B\; -\; 1\; (\varphi \; A\; (x))\; \{\; \backslash \; displaystyle\; y\; =\; \backslash \; phi\; \_\; \{B\}\; ^\; \{-\; 1\}\; (v)\; =\; \backslash \; phi\; \_\; \{B\}\; ^\; \{-\; 1\}\; (\backslash \; phi\; \_\; \{A\}\; (x))\}$, поэтому что для любого вектора из V отображение $\varphi \; B\; -\; 1\; \circ \; \varphi \; A\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{B\}\; ^\; \{-\; 1\}\; \backslash \; circ\; \backslash \; phi\; \_\; \{A\}\}$отображает его набор координат относительно A к его набору координат относительно B. Поскольку это отображение является автоморфизмом на K, поэтому оно имеет ассоциированную квадратную матрицу C. Кроме того, столбец i матрицы C равен $\varphi \; B\; -\; 1\; \circ \; \varphi \; A\; (ei)\; знак\; равно\; \varphi \; B\; -\; 1\; (\alpha \; я)\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{B\}\; ^\; \{-\; 1\}\; \backslash \; circ\; \backslash \; phi\; \_\; \{A\}\; (e\_\; \{i\})\; =\; \backslash \; phi\; \_\; \{B\}\; ^\; \{\; -1\}\; (\backslash \; alpha\; \_\; \{i\})\}$, то есть координатный кортеж α i относительно B.

Таким образом, для любого вектора v в V, если x является набором координат v относительно A, то набор $y\; =\; \varphi \; B\; -\; 1\; (\varphi \; A\; (x))\; =\; C\; x\; \{\backslash \; displaystyle\; y\; =\; \backslash \; phi\; \_\; \{B\}\; ^\; \{-\; 1\}\; (\backslash \; phi\; \_\; \{A\}\; (x))\; =\; Cx\}$- это набор координат v относительно B. Матрица C называется матрицей перехода из От A до B.

Теперь предположим, что T: V → W - линейное преобразование, {α 1,…, α n } - базис для V, а {β 1,…, β m } - базис для W. Пусть φ и ψ - координатные изоморфизмы для V и W соответственно относительно заданных баз. Тогда отображение T 1 = ψ ∘ T ∘ φ является линейным преобразованием из R в R и, следовательно, имеет матрицу t ; его j-й столбец равен ψ (T (α j)) для j = 1,…, n. Эта матрица называется матрицей T относительно упорядоченных базисов {α 1,…, α n } и {β 1,…, β м }. Если η = T (ξ) и y и x - наборы координат для η и ξ, то y = ψ (T (φ (x ))) = tx . Наоборот, если ξ находится в V и x = φ (ξ) является набором координат ξ относительно {α 1,…, α n }, и мы положили y= txи η = ψ (y ), тогда η = ψ (T 1(x)) = T (ξ). То есть, если ξ находится в V, а η находится в W, а x и y - их наборы координат, то y= txтогда и только тогда, когда η = T (ξ).

Теорема Предположим, что U, V и W - векторные пространства конечной размерности, и для каждого выбран упорядоченный базис. Если T: U → V и S: V → W - линейные преобразования с матрицами s и t, то матрица линейного преобразования S ∘ T: U → W (относительно к данным базисам) равно st.

Замена базиса

Теперь мы спросим, ​​что происходит с матрицей T: V → W, когда мы меняем базисы в V и W. Пусть {α 1,…, Α n } и {β 1,…, β m } - упорядоченные базисы для V и W соответственно, и предположим, что нам даны вторая пара оснований {α ′ 1,…, α ′ n } и {β ′ 1,…, β ′ m }. Пусть φ 1 и φ 2 - координатные изоморфизмы, переводящие обычный базис в R в первый и второй базис для V, и пусть ψ 1 и ψ 2 - изоморфизмы, переводящие обычный базис в R в первый и второй базис для W.

Пусть T 1 = ψ 1 ∘ T ∘ φ 1, и T 2 = ψ 2 ∘ T ∘ φ 2 (обе карты принимают R в R ), и пусть t1и t2будут их соответствующими матрицами. Пусть p и q - матрицы автоморфизмов смены координат φ 2 ∘ φ 1 на R и ψ 2 ∘ ψ 1 на R.

Взаимосвязи этих различных отображений друг с другом проиллюстрированы на следующей коммутативной диаграмме. Поскольку мы имеем T 2 = ψ 2 ∘ T ∘ φ 2 = (ψ 2 ∘ ψ 1) ∘ T 1 ∘ (φ 1 ∘ φ 2), и поскольку композиция линейных отображений соответствует умножению матриц, отсюда следует, что

t2= qt1p.

Учитывая, что изменение базиса имеет один раз базисную матрицу и один раз ее инверсию, эти объекты называются 1-со, 1-противоположным вариантом.

Важный случай матрица линейного преобразования - это матрица эндоморфизма , то есть линейное отображение из векторного пространства V в себя: то есть случай, когда W = V. Естественно мы можем взять {β 1,…, β n } = {α 1,…, α n } и {β ′ 1,…, Β ′ m } = {α ′ 1,…, α ′ n }. Матрица линейного отображения T обязательно квадратная.

Изменение базиса

Мы применяем то же изменение базиса, так что q= pи изменение формулы изменения базиса становится

t2= pt1p.

В этой ситуации обратимая матрица pназывается матрицей замены базиса для векторного пространства V, и приведенное выше уравнение говорит, что матрицы t1и t2подобны.

A билинейной формы в векторном пространстве V над полем Rявляется отображением V × V → R, которое является линейным в обоих аргументах. То есть B: V × V → R является билинейным, если карты

$v\; \mapsto \; B\; (v,\; w)\; \{\backslash \; displaystyle\; v\; \backslash \; mapsto\; B\; (v,\; w)\}$

$v\; \mapsto \; B\; (w,\; v)\; \{\backslash \; displaystyle\; v\; \backslash \; mapsto\; B\; (w,\; v)\}$

линейны для каждого w в V. Это определение одинаково хорошо применимо к модулям над коммутативным кольцом с линейными отображениями, являющимися гомоморфизмами модулей.

Матрица Грама G, прикрепленная к базису $\alpha \; 1,\dots ,\; \alpha \; n\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{1\},\; \backslash \; точек,\; \backslash \; alpha\; \_\; \{n\}\}$определяется как

$G\; i,\; j\; =\; B\; (\alpha \; i,\; \alpha \; j).\; \{\backslash \; displaystyle\; G\_\; \{i,\; j\}\; =\; B\; (\backslash \; alpha\; \_\; \{i\},\; \backslash \; alpha\; \_\; \{j\}).\}$

Если $v\; =\; \sum \; ixi\; \alpha \; i\; \{\backslash \; displaystyle\; v\; =\; \backslash \; sum\; \_\; \{\; i\}\; x\_\; \{i\}\; \backslash \; alpha\; \_\; \{i\}\}$и $w\; =\; \sum \; iyi\; \alpha \; i\; \{\backslash \; displaystyle\; w\; =\; \backslash \; sum\; \_\; \{i\}\; y\_\; \{i\}\; \backslash \; alpha\; \_\; \{i\}\; \}$- выражения векторов v, w относительно этого базиса, тогда билинейная форма задается как

$B\; (v,\; w)\; =\; v\; TG\; w.\; \{\backslash \; displaystyle\; B\; (v,\; w)\; =\; v\; ^\; \{\backslash \; mathsf\; \{T\}\}\; Gw.\}$

Матрица будет симметричной, если билинейная форма B является симметричной билинейной формой.

Изменение базиса

Если P - обратимая матрица, представляющая изменение базиса с $\alpha \; 1,\dots ,\; \alpha \; n\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; alpha\; \_\; \{\; n\}\}$до $\alpha \; 1\; \prime ,\dots ,\; \alpha \; n\; \prime \; \{\backslash \; displaystyle\; \backslash \; alpha\; \text{'}\_\; \{1\},\; \backslash \; dots,\; \backslash \; alpha\text{'}\; \_\; \{n\}\}$тогда матрица Грама преобразуется с помощью сравнения матриц

$G\; \text{'}=\; PTGP.\; \{\backslash \; displaystyle\; G\; \text{'}=\; P\; ^\; \{\backslash \; mathsf\; \{T\}\}\; GP.\}$

В теории абстрактного векторного пространства изменение концепции базиса безобидно; кажется, это мало что добавляет науке. Тем не менее, в ассоциативных алгебрах бывают случаи, когда смены базиса достаточно, чтобы превратить гусеницу в бабочку, образно говоря:

• в плоскости расщепленных комплексных чисел есть альтернативный «диагональный базис». Стандартная гипербола xx - yy = 1 становится xy = 1 после изменения базиса. Преобразования плоскости, которые оставляют гиперболы на месте, соответствуют друг другу, по модулю изменение базиса. Контекстная разница достаточно велика, чтобы отделить усиление Лоренца от сопоставление сжатия. Панорамный обзор литературы, посвященной этим сопоставлениям, может быть сделан с использованием основного изменения базиса.
• С вещественными матрицами 2 × 2 можно найти начало каталога линейных алгебр благодаря Артур Кэли. Его соратник Джеймс Кокл выдвинул в 1849 году свою алгебру кокватернионов или расщепленных кватернионов, которые являются той же алгеброй, что и вещественные матрицы 2 × 2, только что построенные на другой матричной основе. И снова концепция смены базиса синтезирует матричную алгебру Кэли и кокватернионы Кокла.
• Смена базиса превращает комплексную матрицу 2 × 2 в бикватернион.

• Вектор координат
• Интегральное преобразование, непрерывный аналог изменения базиса.
• Активное и пассивное преобразование

1. ^Антон (1987, стр. 171)
2. ^Beauregard Fraleigh (1973, стр. 93)
3. ^Неринг (1970, стр. 15)
4. ^Неринг (1970, стр. 15)
5. ^Антон (1987, стр. 74–76)
6. ^Beauregard Fraleigh (1973, стр. 194–195)
7. ^Неринг (1970, стр. 15)
8. ^Антон (1987, стр. 221– 237)
9. ^Beauregard Fraleigh (1973, стр. 240–243)
10. ^Неринг (1970, стр. 50–52)
11. ^«Изменение основы - Учебное пособие по исчислению HMC». www.math.hmc.edu. Архивировано из оригинала 16.07.2016. Проверено 22 августа 2017 г. и объяснение / доказательство «Почему?». www.math.hmc.edu. Проверено 22 августа 2017 г.

• Антон, Ховард (1987), Элементарная линейная алгебра (5-е изд.), Нью-Йорк: Wiley, ISBN 0-471-84819-0
• Beauregard, Raymond A.; Фрали, Джон Б. (1973), Первый курс линейной алгебры: с дополнительным введением в группы, кольца и поля, Бостон: Houghton Mifflin Company, ISBN 0-395-14017-X
• Неринг, Эвар Д. (1970), Линейная алгебра и теория матриц (2-е изд.), Нью-Йорк: Wiley, LCCN 76091646

• Лекция по линейной алгебре Массачусетского технологического института по изменению основы, из MIT OpenCourseWare
• Лекция Академии Хана по изменению основы, из Академии Хана