Антиматроид

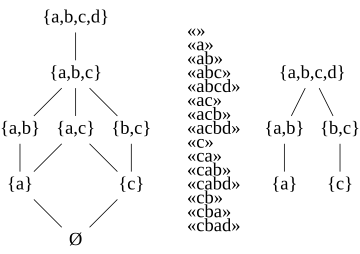
Три вида антиматроида: порядок включения в его семействе допустимых множеств, формальный язык и соответствующий позиционный набор путей.

В математике, антиматроид - это формальная система, описывающая процессы, в которых набор составляется путем включения элементов по одному в время, и в течение которого элемент, будучи доступным для включения, остается доступным до тех пор, пока не будет включен. Антиматроиды обычно аксиоматизируются двумя эквивалентными способами, либо как система множеств, моделирующая возможные состояния такого процесса, либо как формальный язык, моделирующий различные последовательности в какие элементы могут быть включены. Дилворт (1940) был первым, кто изучал антиматроидов, используя еще одну аксиоматизацию, основанную на теории решетки, и они часто заново открывались в других контекстах; см. Korte et al. (1991) за исчерпывающий обзор теории антиматроидов со многими дополнительными ссылками.

Аксиомы, определяющие антиматроидов как системы множеств, очень похожи на аксиомы матроидов, но в то время как матроиды определяются аксиомой обмена (например, базисный обмен или независимые аксиомы обмена множеством), антиматроиды вместо этого определяются аксиомой антиобмена, из которой происходит их название. Антиматроиды можно рассматривать как частный случай гридоидов и полумодулярных решеток, а также как обобщение частичных порядков и распределительных решеток. Антиматроиды эквивалентны по дополнению выпуклой геометрии, комбинаторной абстракции выпуклых множеств в геометрии.

Антиматроиды были применены для моделирования ограничений приоритета в задачах планирования, потенциальных последовательностях событий в симуляциях, планировании задач в искусственном интеллекте и состояниях знаний учащихся-людей.

• 1 Определения
• 2 Примеры
• 3 Пути и базовые слова
• 4 Выпуклая геометрия
• 5 Объединенно-распределительные решетки
• 6 Сверхрешаемые антиматроиды
• 7 Операция объединения и выпуклость измерение
• 8 Перечисление
• 9 Приложения
• 10 Примечания
• 11 Ссылки

Антиматроид может быть определен как конечное семейство F наборов, называемых допустимыми наборами, с следующие два свойства:

• Также возможно объединение любых двух возможных наборов. То есть F закрыто относительно объединений.
• Если S - непустое допустимое множество, тогда существует некоторый x в S такой, что S \ {x} (множество, образованное удалением x из S) также возможно. То есть F - это система доступных множеств.

Антиматроиды также имеют эквивалентное определение как формальный язык, то есть как набор строк, определенных из конечного алфавит из символов. Язык L, определяющий антиматроида, должен удовлетворять следующим свойствам:

• Каждый символ алфавита встречается хотя бы в одном слове L.
• Каждое слово L содержит не более одной копии любого символа.
• Каждый префикс строки в L также находится в L.
• Если s и t - строки в L, и s содержит хотя бы один символ, которого нет в t, тогда в s есть такой символ x, что tx - это другая строка в L.

Если L - антиматроид, определенный как формальный язык, то наборы символов в строках L образуют доступную систему замкнутых множеств. С другой стороны, если F - доступная система замкнутых множеств с объединением, а L - язык строк s со свойством, что набор символов в каждом префиксе s возможен, то L определяет антиматроида. Таким образом, эти два определения приводят к математически эквивалентным классам объектов.

Последовательность обстрела плоского набора точек. Отрезки линии показывают края выпуклой оболочки после того, как некоторые точки были удалены.

• Цепной антиматроид имеет в качестве своего формального языка префиксы одного слова и, поскольку это возможно, устанавливает наборы символы в этих префиксах. Например, цепной антиматроид, определяемый словом «abcd», имеет в качестве своего формального языка строки {ε, «a», «ab», «abc», «abcd»} и в качестве возможного устанавливает множества Ø, {a}, {a, b}, {a, b, c} и {a, b, c, d}.
• Позиционный антиматроид имеет в качестве допустимых наборов нижние наборы конечное частично упорядоченное множество. Согласно теореме Биркгофа о представлении для дистрибутивных решеток, допустимые множества в антиматроиде poset (упорядоченные по включению множества) образуют дистрибутивную решетку, и любая дистрибутивная решетка может быть сформирована таким образом. Таким образом, антиматроиды можно рассматривать как обобщения дистрибутивных решеток. Цепной антиматроид - это частный случай антиматроида по множеству для полного порядка.
• Последовательность обстрелов конечного множества U точек на евклидовой плоскости или в многомерной евклидовой плоскости. пространство - это такой порядок точек, что для каждой точки p существует линия (в евклидовой плоскости или гиперплоскость в евклидовом пространстве), разделяющая p из всех последующих точек последовательности. Эквивалентно, p должна быть вершиной выпуклой оболочки его и всех последующих точек. Последовательности частичного обстрела набора точек образуют антиматроид, называемый обстреливающим антиматроидом. Возможные множества обстреливающего антиматроида - это пересечения U с дополнением выпуклого множества. Каждый антиматроид изоморфен антиматроиду-оболочке из точек в достаточно многомерном пространстве.
• A упорядочение идеального исключения в хордальном графе - это такой порядок его вершин, что для каждой вершины v, соседи v, которые появляются позже v в упорядочении, образуют клику . Префиксы порядков идеального исключения хордального графа образуют антиматроид. Антиматроиды также описывают некоторые другие виды порядка удаления вершин в графах, такие как порядок разборки графов-победителей.

В теоретико-множественной аксиоматизации антиматроидов есть определенные специальные наборы, называемые путями, которые определяют весь антиматроид, в том смысле, что наборы антиматроида являются в точности объединениями путей. Если S - это любой допустимый набор антиматроида, элемент x, который может быть удален из S для образования другого допустимого набора, называется конечной точкой S, а допустимый набор, который имеет только одну конечную точку, называется путем антиматроида. Семейство путей можно частично упорядочить включением множества, формируя позиционный набор путей антиматроида.

Для каждого возможного набора S в антиматроиде и каждого элемента x из S можно найти подмножество путей S, для которого x является конечной точкой: для этого удалите по одному элементы, кроме x до тех пор, пока такое удаление не останется из допустимого подмножества. Следовательно, каждое допустимое множество в антиматроиде является объединением его подмножеств путей. Если S не является путем, каждое подмножество в этом объединении является правильным подмножеством S. Но, если S сам является путем с конечной точкой x, каждое собственное подмножество S, принадлежащее антиматроиду, исключает x. Следовательно, пути антиматроида - это как раз те множества, которые не равны объединениям их собственных подмножеств в антиматроиде. Эквивалентно данное семейство множеств P образует множество путей антиматроида тогда и только тогда, когда для каждого S в P объединение подмножеств S в P имеет на один элемент меньше, чем само S. Если так, то F сам по себе является семейством объединений подмножеств P.

В формальной языковой формализации антиматроида мы также можем идентифицировать подмножество слов, которые определяют весь язык, основные слова. Самые длинные строки в L называются базовыми словами; каждое основное слово образует перестановку всего алфавита. Например, базовые слова антиматроида poset - это линейные расширения данного частичного порядка. Если B - это набор базовых слов, L можно определить из B как набор префиксов слов в B. Часто таким образом удобно определять антиматроидов из базовых слов, но написать аксиоматическое определение слова непросто. антиматроиды в терминах их основных слов.

Если F - система множеств, определяющая антиматроида, где U равно объединению множеств в F, то семейство множеств

$G\; =\; \{U\; \setminus \; S\; \mid \; S\; \in \; F\}\; \{\backslash \; displaystyle\; G\; =\; \backslash \; \{U\; \backslash \; setminus\; S\; \backslash \; mid\; S\; \backslash \; in\; F\; \backslash \}\}$

дополнительный к множествам в F иногда называется выпуклой геометрией и множества в G называются выпуклыми множествами . Например, в антиматроиде-оболочке выпуклые множества являются пересечениями U с выпуклыми подмножествами евклидова пространства, в которое вложено U.

В дополнение к свойствам систем множеств, которые определяют антиматроидов, система множеств, определяющая выпуклую геометрию, должна быть замкнута относительно пересечений, и для любого множества S в G, которое не равно U, должен быть элемент x не в S, который может быть добавлен к S, чтобы сформировать другое множество в G.

Выпуклая геометрия также может быть определена в терминах оператора замыкания τ, который отображает любое подмножество U в его минимальное закрытый суперсет. Чтобы быть оператором замыкания, τ должно иметь следующие свойства:

• τ (∅) = ∅: закрытие пустого множества пусто.
• Любое множество S является подмножеством из τ (S).
• Если S является подмножеством T, то τ (S) должно быть подмножеством τ (T).
• Для любого множества S, τ (S) = τ (τ (S)).

Семейство замкнутых множеств, возникающих в результате операции замыкания этого типа, обязательно замкнуто относительно пересечений. Операторы замыкания, определяющие выпуклые геометрии, также удовлетворяют дополнительной аксиоме антиобмена :

• Если y ≠ z и ни один из них не принадлежит τ (S), но z принадлежит τ (S ∪ {y}), то y не принадлежит τ (S ∪ {z}).

Операция замыкания, удовлетворяющая этой аксиоме, называется антиобменным замыканием . Если S - замкнутое множество в замыкании антиобмена, то аксиома антиобмена определяет частичный порядок на элементах, не принадлежащих S, где x ≤ y в частичном порядке, когда x принадлежит τ (S ∪ {y}). Если x - минимальный элемент этого частичного порядка, то S ∪ {x} замкнуто. То есть семейство замкнутых множеств замыкания против обмена имеет свойство, заключающееся в том, что для любого множества, отличного от универсального, существует элемент x, который может быть добавлен к нему для создания другого замкнутого множества. Это свойство является дополнительным к свойству доступности антиматроидов, и тот факт, что пересечения замкнутых множеств замкнуты, дополняет свойство, что объединение допустимых множеств в антиматроиде возможно. Следовательно, дополнения к замкнутым множествам любого антиобменного замыкания образуют антиматроид.

неориентированные графы, в которых выпуклые множества (подмножества вершин, содержащие все кратчайшие пути между вершинами в подмножестве) образуют выпуклую геометрию в точности графы Птолемея.

Любые два набора в антиматроиде имеют уникальную наименьшую верхнюю границу (их объединение) и уникальная точная нижняя граница (объединение множеств в антиматроиде, содержащихся в них обоих). Следовательно, наборы антиматроида , частично упорядоченные включением множеств, образуют решетку. Различные важные особенности антиматроида можно интерпретировать в терминах теории решетки; например, пути антиматроида - это элементы , не сводимые к объединению, соответствующей решетки, а основные слова антиматроида соответствуют максимальным цепям в решетке. Решетки, которые возникают из антиматроидов таким образом, обобщают конечные дистрибутивные решетки и могут быть охарактеризованы несколькими различными способами.

• Описание, первоначально рассмотренное Дилвортом (1940), касается встречных-неприводимых элементов решетки. Для каждого элемента x антиматроида существует уникальный максимально допустимый набор S x, не содержащий x (S x - это объединение всех допустимых наборов, не содержащих x). S x является встречно-неприводимым, что означает, что это не пересечение любых двух больших элементов решетки: любое большее допустимое множество и любое пересечение больших допустимых множеств содержит x и поэтому не равно S х. Любой элемент любой решетки может быть разложен как пересечение встречающе-неприводимых множеств, часто несколькими способами, но в решетке, соответствующей антиматроиду, каждый элемент T имеет уникальное минимальное семейство встречно-неприводимых множеств S x чья встреча - T; это семейство состоит из множеств S x таких, что T ∪ {x} принадлежит антиматроиду. То есть решетка имеет уникальные взаимно неприводимые разложения.
• Вторая характеристика касается интервалов в решетке, подрешеток, определенных парой элементов решетки x ≤ y и состоящих из всех элементов решетки z с x ≤ z ≤ y. Интервал является атомистическим, если каждый элемент в нем является объединением атомов (минимальные элементы над нижним элементом x), и он является логическим, если он изоморфен решетке все подмножества конечного множества. Для антиматроида каждый атомистический интервал также является логическим.
• В-третьих, решетки, возникающие из антиматроидов, являются полумодулярными решетками, решетками, которые удовлетворяют верхнему полумодулярному закону, который для любых двух элементов x и y, если y покрывает x ∧ y, то x ∨ y покрывает x. Переводя это условие в наборы антиматроида, если набор Y имеет только один элемент, не принадлежащий X, тогда этот один элемент может быть добавлен к X, чтобы сформировать другой набор в антиматроиде. Кроме того, решетка антиматроида обладает свойством пересечения-полудистрибутивности: для всех элементов решетки x, y и z, если x ∧ y и x ∧ z равны, то они также равны x ∧ (y ∨ z). Полумодулярная и встречно-полудистрибутивная решетка называется объединенно-дистрибутивной решеткой.

Эти три характеристики эквивалентны: любая решетка с уникальными встречно-неприводимыми разложениями имеет булевы атомистические интервалы и является объединенно-распределительной, любая решетка с булевыми атомистическими интервалами имеет уникальные встречно-неприводимые разложения и объединяющая дистрибутивная решетка, и любая объединенно-дистрибутивная решетка имеет уникальные встречно-неприводимые разложения и булевы атомистические интервалы. Таким образом, мы можем называть решетку с любым из этих трех свойств дистрибутивной по объединению. Любой антиматроид порождает конечную объединенно-дистрибутивную решетку, и любая конечная объединенно-распределительная решетка происходит от антиматроида таким образом. Другой эквивалентной характеристикой конечных дистрибутивных решеток является то, что они градуированы (любые две максимальные цепи имеют одинаковую длину), а длина максимальной цепи равна количеству встречно-неприводимых элементов решетки. Антиматроид, представляющий конечную объединенно-дистрибутивную решетку, может быть восстановлен из решетки: элементы антиматроида можно принять как встречно-неприводимые элементы решетки, а допустимое множество, соответствующее любому элементу x решетки, состоит из множество встречно-неприводимых элементов y таких, что y не больше или равно x в решетке.

Это представление любой конечной объединенно-дистрибутивной решетки в виде доступного семейства множеств, замкнутых относительно объединений (то есть как антиматроид), можно рассматривать как аналог теоремы о представлении Биркгофа, согласно которой любая конечная дистрибутивная решетка имеет представление в виде семейства множеств, замкнутых относительно объединений и пересечений.

Мотивированные проблемой определения частичных порядков по элементам группы Кокстера, Армстронг (2007) изучал антиматроиды, которые являются также сверхразрешимые решетки. Сверхразрешимый антиматроид определяется полностью упорядоченным набором элементов и семейством наборов этих элементов. В семье обязательно должен быть пустой набор. Кроме того, он должен обладать тем свойством, что если два множества A и B принадлежат семейству, теоретико-множественная разность B \ A непуста, а x является наименьшим элементом B \ A, тогда A ∪ {x} тоже принадлежит семье. Как отмечает Армстронг, любое семейство наборов этого типа образует антиматроида. Армстронг также дает теоретико-решеточную характеристику антиматроидов, которые может образовывать эта конструкция.

Если A и B - два антиматроида, оба описываются как семейство множеств, и если максимальные множества в A и B равны, мы можем сформировать другого антиматроида., соединение A и B следующим образом:

$A\; \vee \; B\; =\; \{S\; \cup \; T\; \mid \; S\; \in \; A\; \wedge \; T\; \in \; B\}.\; \{\backslash \; displaystyle\; A\; \backslash \; vee\; B\; =\; \backslash \; \{S\; \backslash \; cup\; T\; \backslash \; mid\; S\; \backslash \; in\; A\; \backslash \; wedge\; T\; \backslash \; in\; B\; \backslash \}.\}$

Эта операция отличается от операции соединения, рассматриваемой в теоретико-решеточных характеристиках антиматроидов : он объединяет два антиматроида в другой антиматроид, а не объединяет два набора в антиматроиде для формирования другого набора. Семейство всех антиматроидов, у которых есть данный максимальный набор, образует полурешетку с этой операцией соединения.

Соединения тесно связаны с операцией замыкания, которая отображает формальные языки на антиматроиды, где закрытие языка L является пересечением всех антиматроидов, содержащих L в качестве подъязыка. Это замыкание в качестве возможного устанавливает объединения префиксов строк в L. В терминах этой операции закрытия объединение - это замыкание объединения языков A и B.

Каждый антиматроид может быть представлен как объединение семейства цепных антиматроидов или, что эквивалентно, как замыкание набора базовых слов; выпуклая размерность антиматроида A - это минимальное количество цепных антиматроидов (или, что эквивалентно, минимальное количество основных слов) в таком представлении. Если F - семейство цепных антиматроидов, все основные слова которых принадлежат A, то F порождает A тогда и только тогда, когда допустимые множества F включают все пути A. Пути A, принадлежащие одному цепному антиматроиду, должны образовывать chain в poset пути A, так что выпуклая размерность антиматроида равна минимальному количеству цепей, необходимых для покрытия poset пути, что по теореме Дилворта равно ширине poset пути.

Если у кого-то есть представление антиматроида как замыкание набора из d базовых слов, то это представление можно использовать для отображения возможных наборов антиматроида в d-мерное евклидово пространство: назначьте одну координату для каждого базовое слово w, и сделайте значение координаты допустимого множества S длиной самого длинного префикса w, который является подмножеством S. С этим вложением S является подмножеством T тогда и только тогда, когда все координаты для S равны меньше или равно соответствующим координатам T. Следовательно, размерность порядка включения Упорядоченность допустимых множеств не более чем равна выпуклой размерности антиматроида. Однако в целом эти два измерения могут сильно отличаться: существуют антиматроиды с размерностью третьего порядка, но с произвольно большой выпуклой размерностью.

Количество возможных антиматроидов в наборе элементов быстро растет вместе с количеством элементов в наборе. Для наборов из одного, двух, трех и т.д. элементов количество различных антиматроидов составляет

1, 3, 22, 485, 59386, 133059751,... (последовательность A119770 в OEIS ).

Как приоритетность, так и ограничения по времени выпуска в стандартной нотации для теоретических задач планирования могут моделироваться антиматроидами. Boyd Faigle (1990) используйте антиматроиды, чтобы обобщить жадный алгоритм из Юджин Лоулер для оптимального решения задач планирования для одного процессора с ограничениями приоритета, цель которых - минимизировать максимальный штраф, понесенный поздним планированием задача.

Глассерман и Яо (1994) используют антиматроиды для моделирования порядка событий в системах моделирования дискретных событий.

Пармар (2003) использует антиматроидов для моделирования прогресса к цели в искусственном интеллекте планирование задач.

В теории оптимальности грамматики логически эквивалентны антиматроидам (Merchant Ri ggle (2016)).

В математической психологии антиматроиды использовались для описания возможных состояний знаний человека, обучающегося. Каждый элемент антиматроида представляет собой концепцию, которую должен понять учащийся, или класс проблем, которые он или она может правильно решить, а наборы элементов, которые образуют антиматроид, представляют возможные наборы концепций, которые могут быть решены. понимает один человек. Аксиомы, определяющие антиматроид, можно неформально сформулировать как утверждение, что изучение одной концепции никогда не может помешать учащемуся изучить другую концепцию, и что любое возможное состояние знаний может быть достигнуто путем изучения одной концепции за раз. Задача системы оценки знаний состоит в том, чтобы вывести набор понятий, известных данному учащемуся, путем анализа его или ее ответов на небольшой и хорошо подобранный набор проблем. В этом контексте антиматроидов также называют «пространствами обучения» и «пространствами хорошо оцененных знаний».