Кривая таутохрон

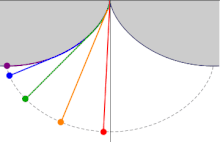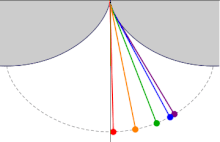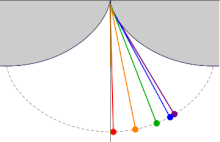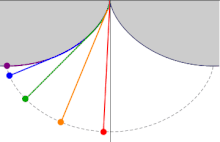
Четыре шара скользят вниз по циклоидной кривой из разных положений, но они достигают дна одновременно. Синие стрелки показывают ускорение точек вдоль кривой. Вверху находится диаграмма время-положение. Объекты, представляющие кривую таутохрон

A таутохрону или кривую изохроны (от греческих префиксов тауто-, означающих то же самое или iso- equal, а chrono time) - это кривая, для которой время, затрачиваемое объектом, скользящим без трения с равномерной гравитацией до самой нижней точки, не зависит от его начала точка на кривой. Кривая представляет собой циклоиду, а время равно π, умноженному на квадратный корень радиуса (круга, образующего циклоиду) сверх ускорения гравитации. Кривая таутохрон связана с кривой брахистохроны, которая также является циклоидой.

• 1 Задача таутохрон
• 2 Решение Лагранжа
• 3 Решение "виртуальной гравитации"
• 4 Решение Абеля
• 5 См. Также
• 6 Ссылки
• 7 Библиография
• 8 Внешние ссылки

Кристиан Гюйгенс, Horologium осцилляторий sive de motu pendulorum, 1673 Именно в левом кубке Pequod, когда мыльный камень старательно кружился вокруг меня, я впервые косвенно поразился тому замечательному факту, что в геометрии все тела скользят по циклоида, например, мой мыльный камень, спустится из любой точки в одно и то же время.

Моби Дик от Герман Мелвилл, 1851 г.

Проблема таутохрон, попытка идентифицировать эту кривую, была решена Христианом Гюйгенсом в 1659 году. Он геометрически доказал в своем Horologium Oscillatorium, первоначально опубликованном в 1673 году, что кривая a циклоида.

На циклоиде, ось которой расположена на перпендикуляре, а вершина находится внизу, времена спуска, когда тело достигает самой низкой точки в вершине после вылета из любой точки на циклоиде равны друг другу...

Гюйгенс также доказал, что время спуска равно времени, которое требуется телу, чтобы упасть вертикально на то же расстояние, что и диаметр круга, образующего циклоиду, умноженный на π / 2. Говоря современным языком, это означает, что время спуска составляет $\pi \; r\; /\; g\; \{\backslash \; displaystyle\; \backslash \; pi\; \{\backslash \; sqrt\; \{r\; /\; g\}\}\}$, где r - радиус круга, генерирует циклоиду, а g - сила тяжести Земли, или, точнее, ускорение свободного падения Земли.

Пять изохронных циклоидальных маятников с разными амплитудами

Это решение позже было использовано для решения проблемы кривой брахистохроны. Иоганн Бернулли решил проблему в статье (Acta Eruditorum, 1697).

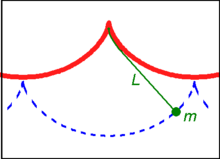
Схема циклоидального маятника

Проблема таутохрона была изучена Гюйгенсом более внимательно, когда стало ясно, что маятник, который следует по круговой траектории, не был изохронным и, следовательно, его маятником Часы будут отсчитывать время по-разному в зависимости от того, как далеко качнулся маятник. Определив правильный путь, Христиан Гюйгенс попытался создать маятниковые часы, в которых использовалась веревка для подвешивания боба и щеки бордюра около вершины веревки, чтобы изменить путь к кривой таутохроны. Эти попытки оказались бесполезными по ряду причин. Во-первых, изгиб струны вызывает трение, изменяя время. Во-вторых, были гораздо более существенные источники временных ошибок, которые подавляли любые теоретические улучшения, которым помогает путешествие по кривой таутохрон. Наконец, «круговая ошибка» маятника уменьшается по мере уменьшения длины поворота, поэтому более совершенные тактовые механизмы спуска могут значительно уменьшить этот источник неточности.

Позже математики Джозеф Луи Лагранж и Леонард Эйлер представили аналитическое решение проблемы.

Если положение частицы параметризуется длиной дуги s (t) от самой низкой точки, кинетическая энергия пропорциональна $s\; \dot{}\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{s\}\}\; ^\; \{2\}.\}$Потенциальная энергия пропорциональна высоте y (s). Один из способов, которым кривая может быть изохроной, - это лагранжиан простого гармонического осциллятора : высота кривой должна быть пропорциональна квадрату длины дуги.

$y\; (s)\; =\; s\; 2,\; \{\backslash \; displaystyle\; y\; (s)\; =\; s\; ^\; \{2\},\}$

где коэффициент пропорциональности был установлен на 1 путем изменения единиц длины. Дифференциальная форма этого отношения:

$dy\; =\; 2\; sds,\; \{\backslash \; displaystyle\; dy\; =\; 2s\; \backslash ,\; ds,\}$

$dy\; 2\; =\; 4\; s\; 2\; ds\; 2\; =\; 4\; y\; (dx\; 2\; +\; dy\; 2),\; \{\backslash \; displaystyle\; dy\; ^\; \{2\}\; =\; 4s\; ^\; \{2\}\; \backslash ,\; ds\; ^\; \{2\}\; =\; 4y\; \backslash ,\; (dx\; ^\; \{2\}\; +\; dy\; ^\; \{2\}),\}$

который исключает s и оставляет дифференциальное уравнение для dx и dy. Чтобы найти решение, проинтегрируйте x через y:

$dxdy\; =\; 1–4\; y\; 2\; y,\; \{\backslash \; displaystyle\; \{dx\; \backslash \; over\; dy\}\; =\; \{\{\backslash \; sqrt\; \{1-4y\}\}\; \backslash \; over\; 2\; \{\backslash \; sqrt\; \{y\}\}\},\}$

$x\; =\; \int \; 1\; -\; 4\; u\; 2\; du,\; \{\backslash \; displaystyle\; x\; =\; \backslash \; int\; \{\backslash \; sqrt\; \{1-4u\; ^\; \{2\}\}\}\; \backslash ,\; du,\}$

где $u\; =\; y\; \{\backslash \; displaystyle\; u\; =\; \{\backslash \; sqrt\; \{y\}\}\}$. Этот интеграл представляет собой площадь под кругом, которую естественным образом можно разрезать на треугольник и круговой клин:

$x\; =\; 1\; 2\; u\; 1\; -\; 4\; u\; 2\; +\; 1\; 4\; arcsin\; \; 2\; u,\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; \{\backslash \; sqrt\; \{1-4u\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; \backslash \; arcsin\; 2u,\}$

$y\; =\; u\; 2.\; \{\backslash \; displaystyle\; y\; =\; u\; ^\; \{2\}.\}$

Чтобы увидеть, что это странно параметризованная циклоида, измените переменные, чтобы разделить трансцендентную и алгебраическую части, определив угол $\theta \; =\; arcsin\; \; 2\; U\; \{\backslash \; Displaystyle\; \backslash \; theta\; =\; \backslash \; arcsin\; 2u\}$. Это дает

$8\; x\; =\; 2\; sin\; \; \theta \; cos\; \; \theta \; +\; 2\; \theta \; =\; sin\; \; 2\; \theta \; +\; 2\; \theta ,\; \{\backslash \; displaystyle\; 8x\; =\; 2\; \backslash \; sin\; \backslash \; theta\; \backslash \; cos\; \backslash \; theta\; +2\; \backslash \; theta\; =\; \backslash \; sin\; 2\; \backslash \; тета\; +2\; \backslash \; тета,\}$

$8\; y\; =\; 2\; грех\; 2\; \; \theta \; =\; 1\; -\; соз\; \; 2\; \theta ,\; \{\backslash \; displaystyle\; 8y\; =\; 2\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; =\; 1-\; \backslash \; cos\; 2\; \backslash \; theta,\}$

, которая является стандартной параметризацией, за исключением шкалы x, y и θ.

Простейшее решение проблемы таутохрон состоит в том, чтобы отметить прямую связь между углом наклона и силой тяжести, ощущаемой частицей на наклоне. Частица, находящаяся под вертикальным углом наклона 90 °, испытывает полное гравитационное ускорение $g\; \{\backslash \; displaystyle\; g\}$, в то время как частица в горизонтальной плоскости испытывает нулевое гравитационное ускорение. При промежуточных углах ускорение частицы за счет "виртуальной силы тяжести" равно $g\; sin\; \; \theta \; \{\backslash \; displaystyle\; g\; \backslash \; sin\; \backslash \; theta\}$. Обратите внимание, что $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$измеряется между касательной к кривой и горизонтом, при этом углы выше горизонтали рассматриваются как положительные углы. Таким образом, $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$изменяется от $-\; \pi \; /\; 2\; \{\backslash \; displaystyle\; -\; \backslash \; pi\; /\; 2\}$до $\pi \; /\; 2\; \{\; \backslash \; displaystyle\; \backslash \; pi\; /\; 2\}$.

Положение массы, измеренное вдоль кривой таутохрон, $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$, должно подчиняться следующему дифференциальному уравнению:

$d\; 2\; sdt\; 2\; =\; -\; \omega \; 2\; s\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; s\}\; \{\{dt\}\; ^\; \{2\}\}\}\; =\; -\; \backslash \; omega\; ^\; \{2\}\; s\}$

который вместе с начальными условиями $s\; (0)\; =\; s\; 0\; \{\backslash \; displaystyle\; s\; (0)\; =\; s\_\; \{0\}\}$и $s\; \prime \; (0)\; =\; 0\; \{\backslash \; displaystyle\; s\; \text{'}(0)\; =\; 0\}$, имеет решение:

$s\; (t)\; =\; s\; 0\; cos\; \; \omega \; t\; \{\backslash \; displaystyle\; s\; (t)\; =\; s\_\; \{0\}\; \backslash \; cos\; \backslash \; omega\; t\; \backslash ,\; \}$

Можно легко проверить, что это решение решает дифференциальное уравнение и что частица достигнет $s\; =\; 0\; \{\backslash \; displaystyle\; s\; =\; 0\}$за время $\pi \; /\; 2.\; \omega \; \{\backslash \; displaystyle\; \backslash \; pi\; /\; 2\; \backslash \; omega\}$из любой начальной позиции $s\; 0\; \{\backslash \; displaystyle\; s\_\; \{0\}\}$. Теперь проблема состоит в том, чтобы построить кривую, которая заставит массу подчиняться описанному выше движению. Второй закон Ньютона показывает, что сила тяжести и ускорение массы связаны следующим образом:

$-\; g\; sin\; \; \theta \; =\; d\; 2\; sdt\; 2\; =\; -\; \omega \; 2\; s\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{\; выровнено\}\; -g\; \backslash \; sin\; \backslash \; theta\; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; s\}\; \{\{dt\}\; ^\; \{2\}\}\}\; \backslash \backslash \; =\; -\; \backslash \; omega\; ^\; \{2\}\; s\; \backslash ,\; \backslash \; end\; \{выровнено\}\; \}\}$

Явное отображение расстояния, $s\; \{\backslash \; displaystyle\; s\}$, вызывает затруднения, но мы можем различать, чтобы получить более удобную форму:

$g\; cos\; \; \theta \; d\; \theta \; =\; \omega \; 2\; ds\; \{\backslash \; displaystyle\; g\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; =\; \backslash \; omega\; ^\; \{2\}\; \backslash ,\; ds\; \backslash ,\}$

или

$ds\; =\; g\; \omega \; 2\; cos\; \; \theta \; d\; \theta \; \{\backslash \; displaystyle\; ds\; =\; \{\backslash \; frac\; \{g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash ,\}$

Это уравнение связывает изменение угла кривой с изменение расстояния по кривой. Теперь мы используем тригонометрию, чтобы связать угол $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$с разностными длинами $dx\; \{\backslash \; displaystyle\; dx\}$, $dy\; \{\backslash \; displaystyle\; dy\}$и $ds\; \{\backslash \; displaystyle\; ds\}$:

$ds\; =\; dx\; cos\; \; \theta \; ds\; =\; dy\; sin\; \; \theta \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; ds\; =\; \{\backslash \; frac\; \{dx\}\; \{\backslash \; cos\; \backslash \; theta\}\}\; \backslash \backslash \; ds\; =\; \{\backslash \; frac\; \{dy\}\; \{\backslash \; sin\; \backslash \; theta\}\}\; \backslash \; end\; \{align\}\}\}$

Замена $ds\; \{\backslash \; displaystyle\; ds\}$с $dx\; \{\backslash \; displaystyle\; dx\}$в приведенном выше уравнении позволяет нам решить для $x\; \{\backslash \; displaystyle\; x\}$через $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$:

$ds\; =\; g\; \omega \; 2\; cos\; \; \theta \; d\; \theta \; dx\; cos\; \; \theta \; =\; g\; \omega \; 2\; cos\; \; \theta \; d\; \theta \; dx\; =\; g\; \omega \; 2\; cos\; 2\; \; \theta \; d\; \theta \; =\; g\; 2\; \omega \; 2\; (cos\; \; 2\; \theta \; +\; 1)\; d\; \theta \; Икс\; знак\; равно\; г\; 4\; \omega \; 2\; (грех\; \; 2\; \theta \; +\; 2\; \theta )\; +\; C\; Икс\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; ds\; =\; \{\backslash \; frac\; \{g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; \{\backslash \; frac\; \{dx\}\; \{\backslash \; cos\; \backslash \; theta\}\}\; =\; \{\backslash \; frac\; \{g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; dx\; =\; \{\backslash \; frac\; \{g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; =\; \{\backslash \; frac\; \{g\}\; \{2\; \backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; left\; (\backslash \; cos\; 2\; \backslash \; theta\; +1\; \backslash \; right)\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; x\; =\; \{\backslash \; frac\; \{g\}\; \{4\; \backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; left\; (\backslash \; sin\; 2\; \backslash \; theta\; +2\; \backslash \; theta\; \backslash \; right)\; +\; C\_\; \{x\}\; \backslash \; end\; \{align\}\}\}$

Точно так же мы также можем выразить $ds\; \{\backslash \; displaystyle\; ds\}$через $dy\; \{\backslash \; displaystyle\; dy\}$и решить для $y\; \{\backslash \; displaystyle\; y\}$в терминах $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$:

$ds\; =\; g\; \omega \; 2\; cos\; \; \theta \; d\; \theta \; dy\; sin\; \; \theta \; =\; g\; \omega \; 2\; соз\; \; \theta \; d\; \theta \; dy\; знак\; равно\; g\; \omega \; 2\; грех\; \; \theta \; соз\; \; \theta \; d\; \theta \; =\; g\; 2\; \omega \; 2\; sin\; \; 2\; \theta \; d\; \theta \; y\; =\; -\; g\; 4\; \omega \; 2\; cos\; \; 2\; \theta \; +\; C\; y\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; ds\; =\; \{\backslash \; frac\; \{g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; \{\backslash \; frac\; \{dy\}\; \{\backslash \; sin\; \backslash \; theta\}\}\; =\; \{\backslash \; frac\; \{\; g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; dy\; =\; \{\backslash \; frac\; \{g\}\; \{\backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; sin\; \backslash \; theta\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; =\; \{\backslash \; frac\; \{g\}\; \{2\; \backslash \; omega\; ^\; \{2\}\}\}\; \backslash \; sin\; 2\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; \backslash \backslash \; y\; =\; -\; \{\backslash \; frac\; \{g\}\; \{4\; \backslash \; omega\; ^\; \{2\; \}\}\}\; \backslash \; cos\; 2\; \backslash \; theta\; +\; C\_\; \{y\}\; \backslash \; end\; \{align\}\}\}$

Подставляя $\varphi \; =\; 2\; \theta \; \{\backslash \; displaystyle\; \backslash \; phi\; =\; 2\; \backslash \; theta\; \backslash ,\}$и $r\; =\; g\; 4\; \omega \; 2\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; frac\; \{g\}\; \{4\; \backslash \; omega\; ^\; \{2\}\}\}\; \backslash ,\}$, мы видим, что это параметрическое уравнение s для $x\; \{\backslash \; displaystyle\; x\}$и $y\; \{\backslash \; displaystyle\; y\}$- это точки на окружности с радиусом $r\; \{\backslash \; displaystyle\; r\}$катится вдоль горизонтальной линии (a циклоида ) с центром круга в координатах $(C\; x\; +\; r\; \varphi ,\; C\; y)\; \{\backslash \; displaystyle\; (C\_\; \{x\}\; +\; r\; \backslash \; phi,\; C\_\; \{y\})\}$:

$x\; =\; r\; (sin\; \; \varphi \; +\; \varphi )\; +\; C\; xy\; =\; -\; r\; cos\; \; \varphi \; +\; C\; y\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; =\; r\; (\backslash \; sin\; \backslash \; phi\; +\; \backslash \; phi)\; +\; C\_\; \{x\}\; \backslash \backslash \; y\; =\; -\; r\; \backslash \; cos\; \backslash \; phi\; +\; C\_\; \{y\}\; \backslash \; end\; \{align\}\}\}$

Обратите внимание, что $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$находится в диапазоне от $-\; \pi \; \le \; \varphi \; \le \; \pi \; \{\backslash \; displaystyle\; -\; \backslash \; pi\; \backslash \; leq\; \backslash \; phi\; \backslash \; leq\; \backslash \; pi\}$. Обычно задается $C\; x\; =\; 0\; \{\backslash \; displaystyle\; C\_\; \{x\}\; =\; 0\}$и $C\; y\; =\; r\; \{\backslash \; displaystyle\; C\_\; \{y\}\; =\; r\}$так, чтобы самая низкая точка кривой совпадала с началом координат. Следовательно:

$x\; =\; r\; (\varphi \; +\; sin\; \; \varphi )\; y\; =\; r\; (1\; -\; cos\; \; \varphi )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; =\; r\; (\backslash \; phi\; +\; \backslash \; sin\; \backslash \; phi)\; \backslash \backslash \; y\; =\; r\; (1-\; \backslash \; cos\; \backslash \; phi)\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Решая для $\omega \; \{\backslash \; displaystyle\; \backslash \; omega\}$и помня, что $T\; =\; \pi \; 2\; \omega \; \{\backslash \; displaystyle\; T\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\; \backslash \; omega\}\}\}$- время, необходимое для спуска, мы находим время спуска через радиус $r\; \{\backslash \; displaystyle\; r\; \}$:

$r\; =\; g\; 4\; \omega \; 2\; \omega \; =\; 1\; 2\; gr\; T\; =\; \pi \; rg\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; r\; =\; \{\backslash \; frac\; \{g\}\; \{4\; \backslash \; omega\; ^\; \{2\}\}\}\; \backslash \backslash \backslash \; omega\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{g\}\; \{r\}\}\}\; \backslash \backslash \; T\; =\; \backslash \; pi\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\}\; \{g\}\}\}\; \backslash \backslash \backslash \; конец\; \{выровнено\}\}\}$

(основано на Прокторе, стр. 135–139)

Нильс Хенрик Абель атаковал обобщенную версию проблемы таутохрон (механическая проблема Абеля), а именно, учитывая функцию T (y), которая определяет общее время спуска для данной стартовой высоты, найдите уравнение кривой, которое даст этот результат. Задача о таутохроне - это частный случай механической задачи Абеля, когда T (y) - постоянная величина.

Решение Абеля начинается с принципа сохранения энергии - поскольку частица не имеет трения и, следовательно, не теряет энергии на тепло, ее кинетическая энергия в любой точке точно равна разности гравитационной потенциальной энергии от его начальной точки. Кинетическая энергия равна $1\; 2\; мв\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; mv\; ^\; \{2\}\}$, и поскольку частица вынуждена двигаться по кривой, ее скорость - это просто $d\; \ell \; dt\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dt\}\}\}$, где $\ell \; \{\backslash \; displaystyle\; \backslash \; ell\}$- расстояние, измеренное по кривой. Аналогичным образом, гравитационная потенциальная энергия, полученная при падении с начальной высоты $y\; 0\; \{\backslash \; displaystyle\; y\_\; \{0\}\; \backslash ,\}$на высоту $y\; \{\backslash \; displaystyle\; y\; \backslash ,\}$равно $mg\; (y\; 0\; -\; y)\; \{\backslash \; displaystyle\; mg\; (y\_\; \{0\}\; -y)\; \backslash ,\}$, таким образом:

$1\; 2\; m\; (d\; \ell \; dt)\; 2\; =\; mg\; (y\; 0\; -\; y)\; d\; \ell \; dt\; =\; \pm \; 2\; g\; (y\; 0\; -\; y)\; dt\; =\; \pm \; d\; \ell \; 2\; g\; (y\; 0\; -\; y)\; dt\; =\; -\; 1\; 2\; g\; (y\; 0\; -\; y)\; d\; dydy\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dt\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; mg\; (y\_\; \{0\}\; -y)\; \backslash \backslash \; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dt\}\}\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{2g\; (y\_\; \{0\}\; -y)\}\}\; \backslash \backslash \; dt\; =\; \backslash \; pm\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{\backslash \; sqrt\; \{2g\; (y\_\; \{0\}\; -y)\}\}\}\; \backslash \backslash \; dt\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2g\; (y\_\; \{0\}\; -y)\}\}\}\; \{\backslash \; frac\; \{d\; \backslash \; ell\; \}\; \{dy\}\}\; \backslash ,\; dy\; \backslash \; end\; \{align\}\}\}$

В последнем уравнении мы ожидали записать расстояние, оставшееся вдоль кривой, как функцию высоты ($\ell \; (y))\; \{\backslash \; displaystyle\; \backslash \; ell\; (y))\}$, распознал, что оставшееся расстояние должно уменьшаться с увеличением времени (таким образом, знак минус), и использовал цепное правило в форме $d\; \ell \; =\; d\; \ell \; dydy\; \{\backslash \; отображает\; tyle\; d\; \backslash \; ell\; =\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\; dy\}$.

Теперь мы интегрируем из $y\; =\; y\; 0\; \{\backslash \; displaystyle\; y\; =\; y\_\; \{0\}\}$в $y\; =\; 0\; \{\backslash \; displaystyle\; y\; =\; 0\}$, чтобы получить общее время, необходимое для падения частицы:

$T\; (y\; 0)\; =\; \int \; y\; =\; y\; 0\; y\; =\; 0\; dt\; =\; 1\; 2\; г\; \int \; 0\; Y\; 0\; 1\; Y\; 0\; -\; ярд\; \ell \; dydy\; \{\backslash \; displaystyle\; T\; (y\_\; \{0\})\; =\; \backslash \; int\; \_\; \{y\; =\; y\_\; \{0\}\}\; ^\; \{y\; =\; 0\}\; \backslash ,\; dt\; =\; \{\backslash \; frac\; \{\; 1\}\; \{\backslash \; sqrt\; \{2g\}\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{y\_\; \{0\}\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{y\_\; \{0\}\; -y\}\}\}\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\; \backslash ,\; dy\}$

Это называется интегральным уравнением Абеля и позволяет нам вычислить общее время, необходимое для того, чтобы частица упала по заданной кривой (для которой $d\; \ell \; dy\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\}$было бы легко вычислить). Но механическая проблема Абеля требует обратного: учитывая $T\; (y\; 0)\; \{\backslash \; displaystyle\; T\; (y\_\; \{0\})\; \backslash ,\}$, мы хотим найти $f\; (y)\; =\; d\; \ell \; dy\; \{\backslash \; displaystyle\; f\; (y)\; =\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\}$, из которого простым способом следует уравнение для кривой. Чтобы продолжить, отметим, что интеграл справа - это свертка из $d\; \ell \; dy\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\}$с $1\; y\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{y\}\}\}\}$и, таким образом, взять преобразование Лапласа с обеих сторон относительно переменной $y\; \{\backslash \; displaystyle\; y\}$:

$L\; [T\; (y\; 0)]\; =\; 1\; 2\; g\; L\; [1\; y]\; F\; (s)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; [T\; (y\_\; \{0\})]\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2g\}\}\}\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{y\}\}\}\; \backslash \; right]\; F\; (s)\}$

где $F\; (s)\; =\; L\; [d\; \ell \; dy]\; \{\backslash \; displaystyle\; F\; (s)\; =\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\; \backslash \; right]\}$Поскольку $L\; [1\; y]\; =\; \pi \; s\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{y\}\}\}\; \backslash \; right]\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{s\}\}\}\}$, теперь у нас есть выражение для преобразования Лапласа $d\; \ell \; dy\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\; \}\}\}$в терминах $T\; (y\; 0)\; \{\backslash \; displaystyle\; T\; (y\_\; \{0\})\; \backslash ,\}$преобразование Лапласа:

$L\; [d\; \ell \; dy]\; знак\; равно\; 2\; г\; \pi \; s\; 1\; 2\; L\; [T\; (y\; 0)]\; \{\backslash \; Displaystyle\; \{\backslash \; mathca\; l\; \{L\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\; \backslash \; right]\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2g\}\; \{\backslash \; pi\}\}\}\; s\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\; \}\; \{\backslash \; mathcal\; \{L\}\}\; [T\; (y\_\; \{0\})]\}$

Это все, что мы можем, без указания $T\; (y\; 0)\; \{\backslash \; displaystyle\; T\; (y\_\; \{0\})\; \backslash ,\}$. Как только $T\; (y\; 0)\; \{\backslash \; displaystyle\; T\; (y\_\; \{0\})\; \backslash ,\}$известен, мы можем вычислить его преобразование Лапласа, вычислить преобразование Лапласа $d\; \ell \; dy\; \{\; \backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\}$, а затем обратное преобразование (или попытка) найти $d\; \ell \; dy\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\; \}\; \{dy\}\}\}$.

Для задачи таутохрон $T\; (y\; 0)\; =\; T\; 0\; \{\backslash \; displaystyle\; T\; (y\_\; \{0\})\; =\; T\_\; \{0\}\; \backslash ,\}$равно постоянный. Поскольку преобразование Лапласа 1 равно $1\; s\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{s\}\}\}$, то есть $L\; [T\; (y\; 0)]\; =\; T\; 0\; s\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; [T\; (y\_\; \{0\})]\; =\; \{\backslash \; frac\; \{T\_\; \{0\}\}\; \{s\}\}\}$, мы находим функцию формы $f\; (Y)\; знак\; равно\; d\; \ell \; dy\; \{\backslash \; displaystyle\; f\; (y)\; =\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\}$:

$F\; (s)\; =\; L\; [d\; \ell \; dy]\; =\; 2\; г\; \pi \; s\; 1\; 2\; L\; [T\; 0]\; =\; 2\; г\; \pi \; T\; 0\; s\; -\; 1\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; F\; (s)\; =\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\; \backslash \; right]\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2g\}\; \{\backslash \; pi\}\}\}\; s\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; mathcal\; \{L\}\}\; [T\_\; \{0\}]\; \backslash \backslash \; =\; \{\; \backslash \; sqrt\; \{\backslash \; frac\; \{2g\}\; \{\backslash \; pi\}\}\}\; T\_\; \{0\}\; s\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

Снова использование преобразования Лапласа выше, мы инвертируем преобразование и заключаем:

$d\; \ell \; dy\; =\; T\; 0\; 2\; g\; \pi \; 1\; y\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; ell\}\; \{dy\}\}\; =\; T\_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{\; 2g\}\}\; \{\backslash \; pi\}\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{y\}\}\}\}$

Можно показать, что циклоида подчиняется этому уравнению. Требуется еще один шаг, чтобы выполнить интеграл по $y\; \{\backslash \; displaystyle\; y\}$, чтобы получить выражение формы пути.

(Симмонс, раздел 54).

• Вариационное исчисление
• Тождество Бельтрами
• Циклоида
• Цепная цепь
• Равномерно ускоренное движение
• Кривая Брахистохрона

1. ^Блэквелл, Ричард Дж. (1986). Часы с маятником Христиана Гюйгенса. Эймс, Айова: Издательство государственного университета Айовы. ISBN 0-8138-0933-9. Часть II, Предложение XXV, стр. 69.

• Симмонс, Джордж, Дифференциальные уравнения с приложениями и историческими примечаниями, McGraw – Hill, 1972. ISBN 0-07-057540-1.
• Проктор, Ричард, Трактат о циклоиде и всех формах циклоидальных кривых (1878), опубликовано Библиотекой Корнельского университета.

• Mathworld