Многомерная выборка

В цифровой обработке сигналов, многомерная выборка представляет собой процесс преобразования функции многомерного переменный в дискретную коллекцию значений функции, измеренной на дискретное множестве точек. В данной статье представлен основной результат из - Petersen и Middleton об условиях совершенно реконструирование волновых чисел -ограниченная функции от своих измерений на дискретной решетке точек. Этот результат, также известный как теорема Петерсена-Миддлтона, является обобщением теоремы выборки Найквиста-Шеннона для выборки одномерных функций с ограниченной полосой пропускания в многомерные евклидовы пространства.

По сути, теорема Петерсена – Миддлтона показывает, что функция с ограниченным волновым числом может быть полностью восстановлена ​​по ее значениям на бесконечной решетке точек при условии, что решетка достаточно тонкая. Теорема дает условия на решетку, при которых возможно точное восстановление.

Как и теорема выборки Найквиста – Шеннона, эта теорема также предполагает идеализацию любой реальной ситуации, поскольку она применима только к функциям, выборка которых производится по бесконечному количеству точек. Идеальная реконструкция математически возможна для идеализированной модели, но только приближение для реальных функций и методов выборки, хотя на практике часто очень хорошее.

• 1 Предварительные мероприятия
• 2 Теорема
• 3 Реконструкция
• 4 Последствия
  • 4.1 сглаживание
  • 4.2 Оптимальные решетки для отбора проб
• 5 приложений
• 6 Ссылки

Рис.1: Гексагональная решетка выборки и ее базисные векторы v 1 и v 2${\ displaystyle \ Lambda}$ Рис. 2: Обратная решетка, соответствующая решетке на рис. 1, и ее базисным векторам u 1 и u 2 (рисунок не в масштабе). ${\ displaystyle \ Gamma}$${\ displaystyle \ Lambda}$

Концепция функции с ограниченной полосой пропускания в одном измерении может быть обобщена до концепции функции с ограничением волнового числа в более высоких измерениях. Напомним, что преобразование Фурье интегрируемой функции на n- мерном евклидовом пространстве определяется как: ${\ Displaystyle е (\ cdot)}$

${\ Displaystyle {\ шляпа {f}} (\ xi) = {\ mathcal {F}} (f) (\ xi) = \ int _ {\ Re ^ {n}} f (x) e ^ {- 2 \ pi i \ langle x, \ xi \ rangle} \, dx}$

где x и ξ - n -мерные векторы, а - скалярное произведение векторов. Говорят, что функция ограничена волновым числом набором, если преобразование Фурье удовлетворяет для. ${\ Displaystyle \ langle х, \ xi \ rangle}$ ${\ Displaystyle е (\ cdot)}$${\ displaystyle \ Omega}$${\ Displaystyle {\ шляпа {f}} (\ xi) = 0}$${\ displaystyle \ xi \ notin \ Omega}$

Точно так же конфигурация равномерно разнесенных точек выборки в одномерном измерении может быть обобщена на решетку в более высоких измерениях. Решетка - это набор точек вида, где { v 1,..., v n } является базисом для. Обратная решетка, соответствующая определяются ${\ displaystyle \ Lambda \ subset \ Re ^ {n}}$${\ displaystyle \ Lambda = \ left \ {\ sum _ {i = 1} ^ {n} a_ {i} v_ {i} \; | \; a_ {i} \ in \ mathbb {Z} \ right \} }$ ${\ Displaystyle \ Re ^ {п}}$ ${\ displaystyle \ Gamma}$${\ displaystyle \ Lambda}$

${\ Displaystyle \ Gamma = \ left \ {\ sum _ {i = 1} ^ {n} a_ {i} u_ {i} \; | \; a_ {i} \ in \ mathbb {Z} \ right \} }$

где векторы выбраны так, чтобы удовлетворить. То есть, если векторы образуют столбцы матрицы и столбцы матрицы, то. Примером выборочной решетки в двумерном пространстве является гексагональная решетка, изображенная на рисунке 1. Соответствующая обратная решетка показана на рисунке 2. Обратная решетка квадратной решетки в двух измерениях является другой квадратной решеткой. В трехмерном пространстве обратная решетка гранецентрированной кубической (ГЦК) решетки является объемно-центрированной кубической (ОЦК) решеткой. ${\ displaystyle u_ {i}}$${\ displaystyle \ langle u_ {i}, v_ {j} \ rangle = \ delta _ {ij}}$${\ displaystyle u_ {i}}$${\ displaystyle A}$${\ displaystyle v_ {i}}$${\ displaystyle B}$${\ displaystyle A = B ^ {- T}}$

Пусть обозначает решетку в и соответствующей обратной решетке. Теорема Петерсена и Миддлтона утверждает, что функция, ограниченная волновым числом набором, может быть точно восстановлена ​​на основе ее измерений при условии, что набор не перекрывается ни с одной из его сдвинутых версий, где сдвиг x является любым ненулевым элементом обратной величины. решетка. Другими словами, может быть точно восстановлен по его измерениям при условии, что для всех. ${\ displaystyle \ Lambda}$${\ Displaystyle \ Re ^ {п}}$${\ displaystyle \ Gamma}$${\ Displaystyle е (\ cdot)}$${\ displaystyle \ Omega \ subset \ Re ^ {n}}$${\ displaystyle \ Lambda}$${\ displaystyle \ Omega}$${\ displaystyle \ Omega + x}$${\ displaystyle \ Gamma}$${\ Displaystyle е (\ cdot)}$${\ displaystyle \ Lambda}$${\ Displaystyle \ Omega \ cap \ {x + y: y \ in \ Omega \} = \ emptyset}$${\ Displaystyle х \ в \ гамма \ setminus \ {0 \}}$

Рис. 3: Поддержка дискретизированного спектра, полученного гексагональной дискретизацией двумерной функции, ограниченной волновым числом круглым диском. Синий кружок представляет собой поддержку исходного поля, ограниченного волновым числом, а зеленые кружки представляют повторения. В этом примере спектральные повторения не перекрываются и, следовательно, нет наложения спектров. Исходный спектр можно точно восстановить из отобранного спектра. ${\ displaystyle {\ hat {f}} _ {s} (\ cdot)}$${\ displaystyle \ Omega}$

Обобщение формулы суммирования Пуассона на более высокие измерения можно использовать, чтобы показать, что выборок функции на решетке достаточно для создания периодического суммирования функции. Результат: ${\ Displaystyle \ {е (х): х \ в \ лямбда \}}$${\ Displaystyle е (\ cdot)}$${\ displaystyle \ Lambda}$ ${\ Displaystyle {\ шляпа {f}} (\ cdot)}$

${\ displaystyle {\ hat {f}} _ {s} (\ xi) \ {\ stackrel {\ mathrm {def}} {=}} \ sum _ {y \ in \ Gamma} {\ hat {f}} \ left (\ xi -y \ right) = \ sum _ {x \ in \ Lambda} | \ Lambda | f (x) \ e ^ {- i2 \ pi \ langle x, \ xi \ rangle},}$

( Уравнение 1 )

где представляет собой объем параллелепипеда, образованного векторами { v 1,..., v n }. Эту периодическую функцию часто называют дискретным спектром, и ее можно интерпретировать как аналог дискретного преобразования Фурье (DTFT) в более высоких измерениях. Если исходный спектр, ограниченный волновым числом, поддерживается на наборе, то функция поддерживается при периодическом повторении сдвига точек на обратной решетке. Если выполняются условия теоремы Петерсена-Миддлтона, то функция равна для всех, и, следовательно, исходное поле может быть точно восстановлено по выборкам. В этом случае реконструированное поле совпадает с исходным полем и может быть выражено в терминах выборок как ${\ displaystyle | \ Lambda |}$ ${\ Displaystyle {\ шляпа {f}} (\ cdot)}$${\ displaystyle \ Omega}$${\ displaystyle {\ hat {f}} _ {s} (\ cdot)}$${\ displaystyle \ Omega}$${\ displaystyle \ Gamma}$${\ Displaystyle {\ шляпа {f}} _ {s} (\ xi)}$${\ Displaystyle {\ шляпа {f}} (\ xi)}$${\ displaystyle \ xi \ in \ Omega}$

${\ displaystyle f (x) = \ sum _ {y \ in \ Lambda} | \ Lambda | f (y) {\ check {\ chi}} _ {\ Omega} (yx)}$,

( Уравнение 2 )

где - обратное преобразование Фурье характеристической функции множества. Эта интерполяционная формула является многомерным эквивалентом интерполяционной формулы Уиттекера – Шеннона. ${\ displaystyle {\ check {\ chi}} _ {\ Omega} (\ cdot)}$ ${\ displaystyle \ Omega}$

В качестве примера предположим, что это круглый диск. На рис. 3 показано, когда выполняются условия теоремы Петерсена-Миддлтона. Мы видим, что спектральные повторения не перекрываются, и, следовательно, исходный спектр можно точно восстановить. ${\ displaystyle \ Omega}$${\ displaystyle {\ hat {f}} _ {s} (\ cdot)}$

Сглаживание

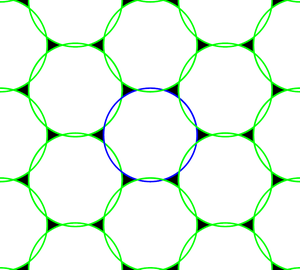Основная статья: Сглаживание Рис. 4: Поддержка дискретизированного спектра, полученного гексагональной дискретизацией двумерной функции, ограниченной волновым числом круглым диском. В этом примере решетка дискретизации недостаточно тонкая и, следовательно, диски перекрываются в спектре дискретизации. Таким образом, спектр внутри, представленный синим кружком, не может быть точно восстановлен из-за перекрытия повторений (показано зеленым), что приводит к наложению спектров. ${\ displaystyle {\ hat {f}} _ {s} (\ cdot)}$${\ displaystyle \ Omega}$ Рис. 5: Пространственное искажение в виде муара. Рис. 6: Изображение кирпичной стены с правильной выборкой.

Теорема дает условия на выборочные решетки для точного восстановления выборки. Если решетки недостаточно тонкие, чтобы удовлетворять условию Петерсена-Миддлтона, то поле не может быть точно восстановлено по образцам в целом. В этом случае мы говорим, что сэмплы могут иметь алиасинг. Снова рассмотрим пример с круглым диском. Если условия Петерсена-Миддлтона не выполняются, поддержка дискретизированного спектра будет такой, как показано на рисунке 4. В этом случае спектральные повторения перекрываются, что приводит к наложению спектров при реконструкции. ${\ displaystyle \ Omega}$

Простую иллюстрацию алиасинга можно получить, изучив изображения с низким разрешением. Полутоновое изображение можно интерпретировать как функцию в двухмерном пространстве. Пример сглаживания показан на изображениях кирпичных узоров на рисунке 5. На изображении показаны эффекты сглаживания, когда условие теоремы выборки не выполняется. Если решетка пикселей недостаточна для сцены, возникает наложение, о чем свидетельствует появление муара на полученном изображении. Изображение на рисунке 6 получается, когда сглаженная версия сцены дискретизируется с той же решеткой. В этом случае условия теоремы выполняются и наложения спектров не происходит.

С.П. Ефимов из МГТУ им. Н. Э. Баумана в 1978 г. нашел способ облегчить ограничения для области спектра. Он считал, что N идентичных решеток выборок произвольно сдвинуты друг к другу. Оптимальная выборка действительна для области спектра, в которой смещенные версии плотно упакованы N раз на обратной решетке. Следовательно, кольцо может быть перекрыто набором шестиугольников вместо одного. Решетка телескопов JWST состоит из 18 шестиугольников. Выборка на 18 смещенных решетках возможна для 2-мерного преобразования Фурье сигнала массива (т.е. для излучаемого сигнала).

Оптимальные решетки для отбора проб

Одна из задач, представляющих интерес при разработке схемы выборки для полей с ограниченным волновым числом, состоит в том, чтобы идентифицировать конфигурацию точек, которая приводит к минимальной плотности выборки, т. Е. Плотности точек выборки на единицу пространственного объема в. Обычно стоимость проведения и хранения измерений пропорциональна используемой плотности выборки. Часто на практике естественным подходом к выборке двумерных полей является их выборка в точках на прямоугольной решетке. Однако это не всегда идеальный выбор с точки зрения плотности выборки. Теорема Петерсена и Миддлтона может быть использована для определения оптимальной решетки для выборочных полей, волновое число которых ограничено заданным набором. Например, можно показать, что решетка с минимальной пространственной плотностью точек, которая допускает идеальные реконструкции полей, ограниченных волновым числом кругового диска, является гексагональной решеткой. Как следствие, гексагональные решетки предпочтительны для измерения изотропных полей в. ${\ Displaystyle \ Re ^ {п}}$ ${\ Displaystyle \ Omega \ subset \ Re ^ {d}}$${\ Displaystyle \ Re ^ {2}}$${\ Displaystyle \ Re ^ {2}}$ ${\ Displaystyle \ Re ^ {2}}$

Оптимальные решетки выборки были изучены в более высоких измерениях. Как правило, оптимальные решетки упаковки сфер идеальны для выборки гладких случайных процессов, в то время как оптимальные решетки, покрывающие сферы, идеальны для выборки грубых стохастических процессов.

Поскольку оптимальные решетки, как правило, неразделимы, проектирование фильтров интерполяции и восстановления требует механизмов проектирования фильтров без тензорного произведения (т. Е. Неразделимых). Прямоугольные шлицы обеспечивают гибкую основу для проектирования таких неразрывных реконструктивных FIR- фильтров, которые можно геометрически подогнать под каждую решетку. Шестигранные сплайны являются обобщением B-сплайнов для двумерных гексагональных решеток. Точно так же в трехмерных и более высоких измерениях сплайны Вороного обеспечивают обобщение B-сплайнов, которые могут использоваться для разработки неразделимых КИХ-фильтров, геометрически адаптированных для любой решетки, включая оптимальные решетки.

Явное построение идеальных фильтров нижних частот (т. Е. Функций sinc ), обобщенных на оптимальные решетки, возможно путем изучения геометрических свойств зон Бриллюэна (т. Е. Указанных выше) этих решеток (которые являются зонотопами ). Этот подход обеспечивает явное представление в замкнутой форме для общих решеток, включая оптимальные решетки выборки. Эта конструкция обеспечивает обобщение фильтра Ланцоша в одномерном пространстве на многомерное решение для оптимальных решеток. ${\ displaystyle \ Omega}$ ${\ displaystyle {\ check {\ chi}} _ {\ Omega} (\ cdot)}$

Теорема Петерсена – Миддлтона полезна при разработке эффективных стратегий размещения датчиков в приложениях, включающих измерение пространственных явлений, таких как сейсмические исследования, мониторинг окружающей среды и измерения пространственного звукового поля.