Функция плотности вероятности  | |||
Кумулятивная функция распределения 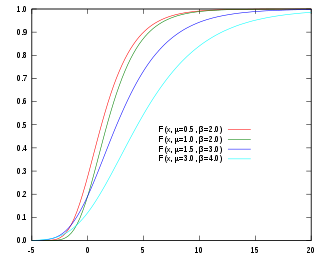 | |||
| Параметры |  местоположение (реальное ). местоположение (реальное ).  масштаб (реальный) масштаб (реальный) | ||
|---|---|---|---|
| Поддержка |  | ||
 . где . где  | |||
| CDF |  | ||
| Среднее |  . где . где  - это константа Эйлера – Маскерони - это константа Эйлера – Маскерони | ||
| Медиана |  | ||
| Mode |  | ||
| Vari ance |  | ||
| Асимметрия |  | ||
| Пр. эксцесс |  | ||
| Энтропия |  | ||
| MGF |  | ||
| CF |  | ||
В теории вероятностей и статистике, Gumbel распределение (Обобщенное распределение экстремальных значений, тип I) используется для моделирования распределения максимального (или минимального) количества выборок различных распределений.
Это распределение можно использовать для представления распределения максимального уровня реки в конкретном году, если существует список максимальных значений за последние десять лет. Это полезно для прогнозирования вероятности возникновения сильного землетрясения, наводнения или другого стихийного бедствия. Потенциальная применимость распределения Гамбеля для представления распределения максимумов относится к теории экстремальных значений, которая указывает на то, что оно, вероятно, будет полезно, если распределение базовых данных выборки будет нормального или экспоненциального типа. В этой статье для моделирования распределения максимального значения используется распределение Гамбеля. Чтобы смоделировать минимальное значение, используйте отрицательное из исходных значений.
Распределение Гамбеля является частным случаем обобщенного распределения экстремальных значений (также известного как распределение Фишера-Типпета). Оно также известно как log- распределение Вейбулла и двойное экспоненциальное распределение (термин, который иногда также используется для обозначения распределения Лапласа ). Это связано с распределением Гомперца : когда его плотность сначала отражается относительно начала координат, а затем ограничивается положительной полупрямой, получается функция Гомперца.
В формулировке скрытой переменной модели полиномиального логита - распространенной в теории дискретного выбора - ошибки скрытых переменных следуют принципу Гамбеля. распространение. Это полезно, потому что разница двух распределенных по Гамбелю случайных величин имеет логистическое распределение.
Распределение Гамбеля названо в честь Эмиля Юлиуса Гамбеля (1891–1966), на основе его оригинальных статей, описывающих распределение.
кумулятивная функция распределения распределение Гамбеля:

стандартное распределение Гамбеля - это случай, когда 


и функция плотности вероятности

В этом случае режим равен 0, медиана равна 

Кумулянты для n>1 даются как

.
Режим - μ, а медиана - 
 ,
,, где 
Стандартное отклонение 

В режиме, где 


 имеет распределение Гамбеля, то условное распределение Y = −X при условии, что Y положительно, или, что эквивалентно, учитывая, что X отрицательно, имеет распределение Гомперца. Cdf G для Y связан с F, cdf для X, формулой
имеет распределение Гамбеля, то условное распределение Y = −X при условии, что Y положительно, или, что эквивалентно, учитывая, что X отрицательно, имеет распределение Гомперца. Cdf G для Y связан с F, cdf для X, формулой  для y>0. Следовательно, плотности связаны соотношением
для y>0. Следовательно, плотности связаны соотношением  : плотность Гомперца пропорциональна отраженной плотности Гамбеля, ограниченной положительной полупрямой.
: плотность Гомперца пропорциональна отраженной плотности Гамбеля, ограниченной положительной полупрямой. и
и  , затем
, затем  (см. Логистическое распределение ).
(см. Логистическое распределение ). и
и  затем
затем  . Обратите внимание, что
. Обратите внимание, что  .
.Теория, относящаяся к обобщенному многомерному распределению log-gamma, обеспечивает многомерная версия распределения Гамбеля.
 Подгонка распределения с доверительным интервалом кумулятивного распределения Гамбеля к максимальным однодневным осадкам в октябре.
Подгонка распределения с доверительным интервалом кумулятивного распределения Гамбеля к максимальным однодневным осадкам в октябре. Гамбель показал, что максимальное значение ( или статистика последнего порядка ) в выборке случайной величины, следующей экспоненциальному распределению минус натуральный логарифм размера выборки, приближается к распределению Гамбеля с увеличением размера выборки.
Таким образом, в гидрологии распределение Гамбеля используется для анализа таких переменных, как месячные и годовые максимальные значения суточных осадков и объемов речного стока, а также для описания засух.
Гамбель также показал, что оценка ⁄ (n + 1) для вероятности события - где r - порядковый номер наблюдаемого значения в серии данных. и n - общее количество наблюдений - это несмещенная оценка кумулятивной вероятности для режима дисбаланса. дань. Поэтому эта оценка часто используется в качестве позиции построения.
. В теории чисел распределение Гамбеля также аппроксимирует количество терминов в случайном разделе целого числа. в качестве скорректированных по тренду размеров максимальных простых промежутков и максимальных промежутков между простыми комбинациями.
В машинном обучении распределение Гамбеля иногда используется для генерации выборок из категориальное распределение.
 Кусок миллиметровой бумаги, включающий распределение Гамбеля.
Кусок миллиметровой бумаги, включающий распределение Гамбеля. До появления программного обеспечения временная бумага использовалась для изображения распределения Гамбеля (см. иллюстрацию). Работа основана на линеаризации кумулятивной функции распределения 
![- \ ln [- \ ln (F)] = (x- \ mu) / \ beta](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ded27e630339c2af35c178b375033ca8022e58)
В статье горизонтальная ось построена в двойном логарифмическом масштабе. Вертикальная ось линейная. Нанося 


.
Поскольку функция квантиля (обратная кумулятивная функция распределения ), 

переменная 




| На Викискладе есть материалы, связанные с: Распределение Гамбеля |