Тенсегрити

Принцип конструкции, основанный на использовании изолированных компонентов при сжатии внутри сети непрерывного напряжения

Простейшая структура тенсегрити (T3- призма). Каждый из трех элементов сжатия (зеленый) симметричен двум другим и симметричен от конца до конца. Каждый конец подсоединяется к трем тросам (красным), которые обеспечивают натяжение и точно определяют положение этого конца так же, как три троса в Skylon определяют нижний конец его конической стойки.

Стерео изображение

Правый кадр

Левый кадр

Вид перекрестным глазом ( )

Параллельный вид ( )

Анимация Аналогичная структура, но с четырьмя элементами сжатия.

Тенсегрити), целостность при растяжении или плавающее сжатие - это принцип конструкции, основанный на системе изолированных компонентов при сжатии внутри сети непрерывное растяжение и расположенные таким образом, что сжатые элементы (обычно стержни или распорки) не соприкасаются друг с другом, в то время как предварительно напряженные растянутые элементы (обычно тросы или связки) очерчивают систему

Этот термин был придуман Бакминстером Фуллером в 1960-х как portmanteau «целостности при растяжении». Другое наименование тенсегрити, floatin g сжатие, использовалось в основном художником-конструктивистом Кеннетом Снельсоном.

• 1 Концепция
• 2 Приложения
• 3 Биология
• 4 История
• 5 Стабильность
  • 5.1 Призмы Тенсегрити
  • 5.2 Икосаэдры тенсегрити
• 6 Патенты
• 7 Основные структуры тенсегрити
• 8 См. Также
• 9 Примечания
• 10 Ссылки
• 11 Библиография
• 12 Дополнительная литература
• 13 Внешняя links

Структуры Tensegrity основаны на комбинации нескольких простых шаблонов проектирования:

• элементы, нагруженные либо при чистом сжатии, либо при чистом растяжении, что означает, что конструкция выйдет из строя только в том случае, если кабели поддаются или стержни изгибаются. Это позволяет оптимизировать свойства материала и геометрию поперечного сечения каждого элемента с учетом конкретной нагрузки, которую он несет.
• предварительная нагрузка или растягивающее предварительное напряжение позволяет кабелям всегда находиться в напряжении, чтобы поддерживать конструкцию целостность.
• механическая стабильность, которая позволяет элементам оставаться в состоянии растяжения / сжатия при увеличении нагрузки на конструкцию. Конструкция также становится более жесткой по мере увеличения натяжения кабеля.

Из-за этих схем ни один элемент конструкции не испытывает изгибающий момент, и в системе отсутствуют напряжения сдвига. Это позволяет создавать исключительно прочные и жесткие конструкции с учетом их массы и поперечного сечения компонентов. Нагрузка по крайней мере некоторых структур тенсегрити вызывает ауксетический ответ и отрицательный коэффициент Пуассона, например Т3-призма и 6-опорный тенсегрити икосаэдр.

Skylon на Фестивале Британии, 1951

Концептуальный строительный блок тенсегрити можно увидеть в Skylon 1951 года. Шесть тросов, по три на каждом конце, удерживают башню на месте. Три кабеля, подключенные к дну, «определяют» его местоположение. Остальные три кабеля просто удерживают его в вертикальном положении.

Тенсегрити-структура с тремя стержнями (показанная справа) построена на этой более простой структуре: концы каждого зеленого стержня выглядят как верх и низ Скайлона. Пока угол между любыми двумя тросами меньше 180 °, положение стержня четко определено. В то время как три кабеля - это минимум, необходимый для устойчивости, дополнительные кабели могут быть прикреплены к каждому узлу в эстетических целях или для обеспечения дополнительной устойчивости. Например, Needle Tower Снельсона использует повторяющийся шаблон, построенный с использованием узлов, каждый из которых подключен к 5 кабелям.

Элеонора Хартни отмечает, что визуальная прозрачность является важным эстетическим качеством этих структур. Коркмаз и др. утверждал, что легкие структуры тенсегрити подходят для адаптивной архитектуры.

Тенсегритис увидел более широкое применение в архитектуре, начиная с 1960-х годов, когда и спроектировал комплекс Spodek arena (в Катовице, Польша ), как одна из первых крупных структур, использующих принцип тенсегрити. Крыша имеет наклонную поверхность, удерживаемую системой тросов, удерживающих ее периметр. Принципы тенсегрити также использовались в Дэвида Гейгера в Сеуле Olympic Gymnastics Arena (для летних Олимпийских игр 1988 года ) и Georgia Dome (для летних Олимпийских игр 1996 г. ). Тропикана Филд, дом бейсбольной команды высшей лиги Tampa Bay Rays, также имеет куполообразную крышу, поддерживаемую большой тенсегрити.

Самый большой мост тенсегрити в мире, мост Курилпа - Брисбен

4 октября 2009 года мост Курилпа открылся через реку Брисбен в Квинсленде, Австралия. Вантовый мост с несколькими мачтами, основанный на принципах тенсегрити, в настоящее время является крупнейшим в мире мостом тенсегрити.

Выставка конструкции высотой 12 м в наукограде, Калькутта.

С начала 2000-х годов Tensegrities также привлекала внимание робототехников из-за их потенциала в разработке легких и устойчивых роботов.. Многочисленные исследователи изучали тенсегрити роверы, био-имитирующие роботы и модульные мягкие роботы. Самым известным роботом Тенсегрити является Super Ball, марсоход для исследования космоса, который в настоящее время разрабатывается в NASA Ames.

Биотенсегрити, термин, придуманный доктором Стивеном Левином, представляет собой приложение тенсегрити. принципы к биологическим структурам. Биологические структуры, такие как мышцы, кости, фасции, связки и сухожилия или жесткие и эластичные клеточные мембраны, становятся прочными благодаря унисону напряженных и сжатых частей. костно-мышечная система поддерживает напряжение в непрерывной сети мышц и соединительных тканей, в то время как кости обеспечивают прерывистую поддержку при сжатии. Даже человеческий позвоночник, который на первый взгляд кажется набором позвонков, опирающихся друг на друга, на самом деле представляет собой структуру тенсегрити.

Дональд Э. Ингбер разработал теория тенсегрити для описания многочисленных явлений, наблюдаемых в молекулярной биологии. Например, выраженные формы клеток, будь то их реакции на приложенное давление, взаимодействия с субстратами и т. Д., Все можно математически смоделировать, представив цитоскелет клетки как тенсегрити. Кроме того, геометрические узоры, встречающиеся в природе (спираль ДНК, геодезический купол вольвокса, бакминстерфуллерен и др.), Также можно понять, применив принципы тенсегрити к спонтанной самосборке соединений, белков и даже органов. Эта точка зрения подтверждается тем, как взаимодействие натяжения-сжатия тенсегрити минимизирует материал, необходимый для поддержания стабильности и достижения структурной упругости. Следовательно, естественный отбор, скорее всего, будет благоприятствовать биологическим системам, организованным по типу тенсегрити.

Как объясняет Ингбер:

Несущие растяжение элементы в этих структурах - будь то купола Фуллера или скульптуры Снельсона - отображают кратчайшие пути между соседними элементами (и поэтому по определению расположены геодезически). Силы натяжения естественным образом передаются на кратчайшее расстояние между двумя точками, поэтому элементы структуры тенсегрити расположены точно так, чтобы лучше всего выдерживать нагрузку. По этой причине структуры тенсегрити обладают максимальной силой.

В эмбриологии Ричард Гордон предположил, что волны эмбриональной дифференцировки распространяются «органеллой дифференциации», где цитоскелет собран в бистабильную структуру тенсегрити на апикальном конце клеток, называемую «расщепителем состояний клетки».

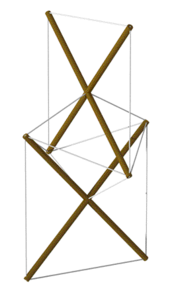Дизайн X-модуля Кеннета Снельсона 1948 года, воплощенный в виде двухкомпонентного модуль колонка

истоки тенсегрити является спорной. Многие традиционные конструкции, такие как каяки «кожа на раме» и сёдзи, используют элементы растяжения и сжатия аналогичным образом.

В 1948 году художник Кеннет Снельсон создал свою новаторскую «X-Piece» после художественных изысканий в Black Mountain College (где Бакминстер Фуллер был лекции) и в других местах. Несколько лет спустя термин «тенсегрити» был придуман Фуллером, наиболее известным своими геодезическими куполами. На протяжении всей своей карьеры Фуллер экспериментировал с включением компонентов, работающих на растяжение, в свою работу, например, в конструкции своих домов dymaxion.

Инновация 1948 года Снельсона подтолкнула Фуллера к немедленному заказу мачты у Снельсона. В 1949 году Фуллер разработал тенсегрити- икосаэдр на основе этой технологии, и он и его ученики быстро разработали дополнительные конструкции и применили эту технологию для строительства куполов. После перерыва Снельсон также создал множество скульптур, основанных на концепциях тенсегрити. Его основная работа началась в 1959 году, когда состоялась основная выставка в Музее современного искусства. На выставке MOMA Фуллер показал мачту и некоторые другие свои работы. На этой выставке Снельсон, после обсуждения с Фуллером и организаторами выставки кредита на мачту, также показал некоторые работы в витрине.

Самым известным произведением Снельсона является его 18-метровая Игольная башня. 1968 года.

Русский художник Вячеслав Колейчук утверждал, что идею тенсегрити первым изобрел Карлис Йохансонс (lv ), советский авангард художник латышского происхождения, внесший несколько работ на главную выставку русского конструктивизма в 1921 году. Заявление Колейчук поддержала Мария Гоф, например произведений конструктивистской выставки 1921 года. Снельсон признал, что конструктивисты оказали влияние на его работу (вопрос?). Французский инженер Давид Жорж Эммерих также отметил, что работа Карлиса Йохансона (и идеи промышленного дизайна), казалось, предвидела концепции тенсегрити.

Призмы тенсегрити

Тенсегрити с тремя стержнями конструкция (3-сторонняя призма) имеет свойство, заключающееся в том, что для заданной (общей) длины «стержня» сжимающего элемента (всего их три) и данной (общей) длины «жилы» натяжного кабеля (всего шесть), соединяющих концы стержней вместе, существует определенное значение для (общей) длины сухожилия, соединяющего вершины стержней с соседними основаниями стержней, которое заставляет конструкцию сохранять стабильную форму. Для такой конструкции несложно доказать, что треугольник, образованный вершинами стержней, и треугольник, образованный основаниями стержней, повернут друг относительно друга на угол 5π / 6 (радиан).

Султан и др. проанализировали стабильность («предварительное напряжение») нескольких двухэтапных структур тенсегрити.

Икосаэдры тенсегрити

Математическая модель икосаэдра тенсегрити Различные формы икосаэдров тенсегрити, в зависимости от соотношение между длинами сухожилий и распорок.

Многогранник, который непосредственно соответствует геометрии икосаэдра тенсегрити, называется икосаэдром Джессена. Его сферическая динамика вызвала особый интерес Бакминстера Фуллера, который назвал его преобразования расширения-сжатия вокруг устойчивого равновесия движением джиттербага.

Ниже приводится математическая модель для фигур, связанных с tensegrity икосаэдр, объясняющее, почему это устойчивая конструкция, хотя и с бесконечно малой подвижностью.

Рассмотрим куб со стороной 2d с центром в начале координат. Поместите распорку длиной 2l в плоскости каждой грани куба так, чтобы каждая распорка была параллельна одному краю грани и центрировалась на грани. Кроме того, каждая стойка должна быть параллельна стойке на противоположной грани куба, но ортогональна всем остальным стойкам. Если декартовы координаты одной стойки равны $(0,\; d,\; l)\; \{\backslash \; displaystyle\; (0,\; d,\; l)\}$и $(0,\; d,\; -\; l)\; \{\backslash \; displaystyle\; (0,\; d,\; -l)\}$, его параллельная стойка будет, соответственно, $(0,\; -\; d,\; -\; l)\; \{\backslash \; displaystyle\; (0,\; -d,\; -l)\; \}$и $(0,\; -\; d,\; l)\; \{\backslash \; displaystyle\; (0,\; -d,\; l)\}$. Координаты концов (вершин) других стоек получаются перестановкой координат, например, $(0,\; d,\; l)\; \to \; (d,\; l,\; 0)\; \to \; (l,\; 0,\; d)\; \{\backslash \; displaystyle\; (0,\; d,\; l)\; \backslash \; rightarrow\; (d,\; l,\; 0)\; \backslash \; rightarrow\; (l,\; 0,\; d)\}$(вращательная симметрия на главной диагонали куба).

Расстояние s между любыми двумя соседними вершинами (0, d, l) и (d, l, 0) равно

$s\; 2\; =\; (d\; -\; l)\; 2\; +\; d\; 2\; +\; l\; 2\; =\; 2\; (d\; -\; 1\; 2\; l)\; 2\; +\; 3\; 2\; l\; 2\; \{\backslash \; displaystyle\; s\; ^\; \{2\}\; =\; (dl)\; ^\; \{2\}\; +\; d\; ^\; \{2\}\; +\; l\; ^\; \{2\}\; =\; 2\; \backslash \; left\; (d\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash ,\; l\; \backslash \; right)\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash ,\; l\; ^\; \{2\}\}$

Представьте себе эту фигуру, построенную из стоек заданной длины 2l и сухожилия (соединяющие соседние вершины) заданной длины s, причем $s>3\; 2\; l\; \{\backslash \; displaystyle\; s>\{\backslash \; sqrt\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\; \backslash ,\; l\}$. Отношение говорит нам, что есть два возможных значения для d: одно реализуется путем сдвигания распорок вместе, другое - путем их растягивания. Например, для $s\; =\; 2\; l\; \{\backslash \; displaystyle\; s\; =\; \{\backslash \; sqrt\; \{2\}\}\; \backslash ,\; l\}$минимальная фигура (d = 0) - это регулярный октаэдр, а максимальная фигура (d = l) является квазирегулярным кубооктаэдром. В cas е $d\; =\; 1\; 2\; (5-1)\; l\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (\{\backslash \; sqrt\; \{5\}\}\; -\; 1)\; l\}$мы имеем s = 2d, поэтому выпуклая оболочка фигуры золотого сечения ($d\; =\; \varphi \; \{\backslash \; displaystyle\; d\; =\; \backslash \; phi\}$) является правильный икосаэдр. Поскольку ни одна статья о кинематике многогранников не была бы полной без ссылки на Кокстера, здесь уместно отметить, что к 1940 году (до икосаэдра Джессена или открытия икосаэдра тенсегрити) Кокстер уже показал, как можно получить двенадцать вершин икосаэдра, разделив двенадцать ребер октаэдра в соответствии с золотым сечением, как одну из непрерывных серий (как правило, неправильных) икосаэдров с гранями, состоящими из восьми равносторонних треугольников и двенадцати равнобедренных. треугольники, от кубооктаэдра до октаэдра (как предельные случаи), которые могут быть получены с помощью такого процесса деления.

В частном случае $s\; =\; 3\; 2\; l\; \{\backslash \; displaystyle\; s\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\; \backslash ,\; l\}$две крайние точки совпадают, и $d\; =\; 1\; 2\; l\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash ,\; l\}$, поэтому фигура представляет собой устойчивый тенсегрити-икосаэдр.

Поскольку икосаэдр тенсегрити представляет собой экстремальную точку указанного выше отношения, он имеет бесконечно малую подвижность: небольшое изменение длины s сухожилия (например, путем растяжения сухожилий) приводит к гораздо большему изменению расстояния 2г подкосов.

• США Патент 3063521, «Структуры, обеспечивающие целостность при растяжении», 13 ноября 1962 г., Бакминстер Фуллер.
• Патент Франции № 1,377,290, «Construction de Reseaux Autotendants», 28 сентября 1964 г., Дэвид Жорж Эммерих.
• Патент Франции № 1377291, «Structures Linéaires Autotendants», 28 сентября 1964 г., Дэвид Джордж Эммерих.
• США Патент 3139957, «Подвесное здание» (также называемое осиной), 7 июля 1964 г., Бакминстер Фуллер.
• США. Патент 3169611, «Непрерывное растяжение, структура прерывистого сжатия», 16 февраля 1965 г., Кеннет Снельсон.
• США. Патент 3866366, «Несимметричные структуры натяжения и целостности», 18 февраля 1975 г., Бакминстер Фуллер.

• 

  Простейшая структура тенсегрити, 3-призма

• 

  Другая 3-призма

• 

  Аналогичная структура, но с четырьмя элементами сжатия

• 

  Призма Прото-Тенсегрити, Карл Иогансон, 1921

• 

  Икосаэдр Тенсегрити, Бакминстер Фуллер, 1949

• 

  Тетраэдр Тенсегрити, Франческо делла Салла, 1952

• 

  Tensegrity X-Module Tetrahedron, Кеннет Снельсон, 1959

• 

  Художественная скульптура Кеннета Снелсона в «Игольной башне».

• 

  Dissipate, художественная скульптура башни в виде песочных часов, включающая структуру тенсегрити, построенная в AfrikaBurn, 2015, Burning Man региональном мероприятии

• 

  Робот NASA SUPERball Tensegrity является ранним прототипом для приземлиться на другой планете без подушки безопасности, и тогда будьте мобильны, чтобы исследовать. Структура тенсегрити обеспечивает структурную податливость, поглощая силы удара при приземлении, и движение создается за счет изменения длины кабеля, 2014 г.

• 

  Купол тенсегрити, сделанный из садовых кольев и нейлонового шпагата, построен во дворе дома, 2009 г.

• Мост - структура, построенная так, чтобы преодолевать физические препятствия
• Облако Девять, гигантские парящие в небе сферы тенсегрити, названные Бакминстером Фуллером
• Гиперболоидная структура
• Теория взаимодействия акторов
• Седловая крыша
• Космический каркас - Жесткая трехмерная несущая ферменная конструкция
• Synergetics
• Предел прочности
• Растягивающая конструкция
• Тонкостенная конструкция

• Фуллер, Р. Бакминстер (1982) [1975]. Синергетика: исследования геометрии мышления. I. Макмиллан. ISBN 978-0-02-065320-2.
• - (1983) [1979]. Синергетика 2: Дальнейшие исследования геометрии мышления. 2. Макмиллан. ISBN 978-0-02-092640-5.Онлайн
• Фуллер, Бакминстер (1961). "Тенсегрити". Ежегодное портфолио и новости искусства (4): 112–127, 144, 148.
• Фуллер, Р. Бакминстер; Маркс, Роберт В. (1973) [1960]. Димаксионный мир Бакминстера Фуллера. Якорные книги. Рис. 261–280. ISBN 978-0385018043.Хороший обзор объема тенсегрити с точки зрения Фуллера и интересный обзор ранних структур с тщательной атрибуцией большую часть времени.
• Гомес- Хауреги, Валентин (2007). Тенсегридад. Estructuras Tensegríticas en Ciencia y Arte (на испанском языке). Сантандер: Университет Кантабрии. ISBN 978-84-8102-437-1.
• Гомес-Хауреги, Валентин (2010). Структуры тенсегрити и их применение в архитектуре. Сантандер: Служба публикаций Университета Кантабрии. ISBN 978-84-8102-575-0.
• Коркмаз, Синан; Бел Хадж Али, Низар; Смит, Ян Ф.С. (2011). «Конфигурация системы контроля устойчивости к повреждениям моста Тенсегрити». Передовая инженерная информатика. 26 : 145. doi : 10.1016 / j.aei.2011.10.002.
• Коркмаз, Синан; Бел Хадж Али, Низар; Смит, Ян Ф.С. (Июнь 2011 г.). «Определение стратегий контроля устойчивости к повреждениям активной структуры тенсегрити» (PDF). Инженерные сооружения. 33 (6): 1930–9. CiteSeerX 10.1.1.370.6243. doi : 10.1016 / j.engstruct.2011.02.031. Архивировано из оригинала (PDF) 29 сентября 2011 года.
• Lalvani, Haresh, ed. (1996). «Истоки тенсегрити: взгляды Эммериха, Фуллера и Снельсона». Международный журнал космических структур. 11 (1–2): 27–55. DOI : 10.1177 / 026635119601-204. S2CID 114004009.
• Juan, S.J.; Тур, Дж. М. (июль 2008 г.). «Фреймворки тенсегрити: обзор статического анализа». Теория механизмов и машин. 43 (7): 859–881. CiteSeerX 10.1.1.574.7510. doi : 10.1016 / j.mechmachtheory.2007.06.010.

• Ди Карло, Бьяджо. "СТРУКТУРА ТЕНСЕГРАЛИ". Quaderni di Geometria Sinergetica, Pescara 2004. http://www.biagiodicarlo.com
• Эдмондсон, Эми. Более полное объяснение, EmergentWorld LLC, 2007. Более ранняя версия доступна в Интернете по адресу https://web.archive.org/web/20031002084349/http://www.angelfire.com/mt/marksomers/40.html
• Forbes, Питер (2010) [2006]. «9. Система построения« толкай и тяни »». Нога геккона: как ученые берут отрывок из книги природы. Харпер Коллинз. С. 197–230. ISBN 978-0-00-740547-3.
• Ханаор, Ариэль (1997). «13. Тенсегрити: теория и применение». В Габриэле, Ж. Франсуа (ред.). За пределами куба: архитектура космических рамок и многогранников. Вайли. С. 385–408. ISBN 978-0-471-12261-6.
• Кеннер, Хью (1976). Геодезическая математика и как ею пользоваться. Калифорнийский университет Press. ISBN 978-0520029248.Отпечаток 2003 г. ISBN 0520239318. Это хорошая отправная точка для изучения математики тенсегрити и построения моделей.
• Масич, Миленко; Скелтон, Роберт Э.; Гилл, Филип Э. (август 2005 г.). «Формообразование алгебраического тенсегрити». Международный журнал твердых тел и структур. 42 (16–17): 4833–58. doi : 10.1016 / j.ijsolstr.2005.01.014.Они представляют замечательный результат, заключающийся в том, что любое линейное преобразование тенсегрити также является тенсегрити.
• ( 2003 г.). «Историческое обозрение: вирусы, кристаллы и геодезические купола».. 28 (2): 86–90. DOI : 10.1016 / S0968-0004 (02) 00007-5. PMID 12575996.
• Мотро, Р. (1992). «Системы тенсегрити: современное состояние». Международный журнал космических структур. 7 (2): 75–84. DOI : 10.1177 / 026635119200700201. S2CID 107820090.
• Пью, Энтони (1976). Введение в тенсегрити. Калифорнийский университет Press. ISBN 978-0-520-03055-8. Архивировано из оригинального 4 мая 2008 г. Получено 9 мая 2008 г.
• Снельсон, Кеннет (ноябрь 1990 г.). "Письмо Р. Мотро". Международный журнал космических структур.
• Souza, Thales R.; Fonseca, Sérgio T.; Gonçalves, Gabriela G.; Окарино, Юлиана М.; Манчини, Мариса К. (октябрь 2009 г.). «Престресс проявляется пассивным одновременным натяжением в голеностопном суставе». Журнал биомеханики. 42 (14): 2374–80. doi : 10.1016 / j.jbiomech.2009.06.033. PMID 19647832.
• Vilnay, Oren, Cable Nets and Tensegric Shells: Analysis and Design Applications, New York: Ellis Horwood Ltd., 1990.
• Ван, Бин-Бинг (1998). «Стойко-тросовые системы: Часть I - Тенсегрити». Журнал исследований конструкционной стали. 45 (3): 281–9. doi : 10.1016 / S0143-974X (97) 00075-8.
• Вилкен, Тимоти. В поисках дара Тенсегрити, TrustMark, 2001.

На Викискладе есть медиафайлы, связанные с Тенсегрити.

• Научными публикациями в области Тенсегрити Швейцарского федерального технологического института ( EPFL), Лаборатория прикладных вычислений и механики (IMAC)
• Сайт Стивена Левина о биотенсегрити Несколько статей хирурга-ортопеда по механике тенсегрити биологических структур от вирусов до позвоночных.