Круглое сечение

трехосный эллипсоид с круглым сечением

В геометрии круговое сечение - это круг на поверхности квадрики (такой как эллипсоид или гиперболоид ). Это особое сечение квадрики плоскость, так как эта окружность является пересечением с квадрикой плоскости, содержащей окружность.

Любое плоское сечение сферы считается круглым сечением, если оно содержит не менее 2 точек. Любая квадрика вращения содержит окружности в виде сечений с плоскостями, ортогональными его оси; он не содержит других кругов, если это не сфера. Более скрыты круги на других квадриках, таких как трехосные эллипсоиды, эллиптические цилиндры и т. Д. Тем не менее верно, что:

• Любая квадратичная поверхность, содержащая эллипсы, также содержит круги.

Точно так же все квадратичные поверхности содержат окружности, кроме параболических и гиперболических цилиндров и гиперболических параболоидов.

Если квадрика содержит окружность, то каждое пересечение квадрики с плоскостью, параллельной этой окружности, также является окружностью при условии, что она содержит минимум два балла. За исключением сфер, окружности, содержащиеся в квадрике, если они есть, все параллельны одной из двух неподвижных плоскостей (которые равны в случае квадрики вращения).

Круглые сечения используются в кристаллографии.

• 1 Использование проективной геометрии
• 2 Определение круговых сечений квадрики
• 3 Трехосный эллипсоид
• 4 Эллиптический гиперболоид одного листа
• 5 Эллиптический цилиндр
• 6 Эллиптический параболоид
• 7 Эллиптический гиперболоид из двух листов
• 8 Эллиптический конус
• 9 Литература
• 10 Внешние ссылки

Круговые сечения квадрики могут быть вычислены из неявного уравнения квадрики, как это делается в следующих разделах. Их также можно охарактеризовать и изучить с помощью синтетической проективной геометрии.

. Пусть C - пересечение квадратичной поверхности Q и плоскости P. В этом разделе Q и C являются поверхностями в трехмерное евклидово пространство, которое расширено до проективного пространства по комплексным числам. Согласно этим гипотезам кривая C является окружностью тогда и только тогда, когда ее пересечение с плоскостью на бесконечности включено в омбилический (бесконечно удаленная кривая уравнения $x\; 2\; +\; y\; 2\; +\; z\; 2\; =\; 0\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; =\; 0\}$).

Первый случай, который следует рассмотреть, - это когда пересечение Q с плоскостью на бесконечности состоит из одной или двух действительных прямых, то есть когда Q либо гиперболический параболоид, a параболический цилиндр или гиперболический цилиндр. В этом случае бесконечно удаленные точки C являются действительными (пересечение реальной плоскости с действительными прямыми). Таким образом, плоские сечения Q не могут быть окружностями (ни эллипсами ).

Если Q является сферой, ее пересечение с бесконечно удаленной плоскостью является омбилическим, и все плоские сечения являются окружностями.

Если Q является поверхностью вращения, ее пересечение с омбиликой состоит из пары комплексно сопряженных точек (которые являются двойными точками ). Реальная плоскость содержит эти две точки тогда и только тогда, когда она перпендикулярна оси вращения. Таким образом, круглые сечения представляют собой плоские сечения плоскостью, перпендикулярной оси, которые имеют по крайней мере две действительные точки.

В остальных случаях пересечение Q с омбиликой состоит из двух разных пар комплексно сопряженных точек. Поскольку C - кривая степени два, ее пересечение с бесконечно удаленной плоскостью состоит из двух точек, возможно, равных. Таким образом, кривая C является окружностью, если эти две точки являются одной из этих двух пар комплексно сопряженных точек на омбилике. Каждая из этих пар определяет реальную линию (проходящую через точки), которая является пересечением P с плоскостью на бесконечности. Таким образом, у каждого есть круговое сечение, если и только C имеет по крайней мере две вещественные точки, а P содержит одну из этих прямых на бесконечности (то есть, если P параллельна одному из двух направлений, определяемых этими прямыми на бесконечности).

Чтобы найти плоскости, которые содержат круговые сечения данной квадрики, используются следующие операторы:

(S:) Если точки пересечения квадрики и сферы лежат в паре плоскостей, то кривая пересечения состоит из двух окружностей.

(P :) Если пересечение плоскости и квадрики является окружностью, чем любая параллельная плоскость, которая содержит не менее двух точек квадрики, также пересекает квадику по окружности.

Следовательно, стратегия обнаружения круговых секций такова:

1) Найдите сферу, которая пересекает квадрика в паре плоскостей и

2) Плоскости, параллельные обнаруженным, доставляют оставшиеся круглые сечения.

трехосный эллипсоид с круговыми сечениями (синий и зеленый) и вспомогательная сфера (красный), которая пересекает квадрику в синих кругах Эллипсоид, пересекаемый сферами:

Для эллипсоида остроумия h уравнение

$x\; 2\; a\; 2\; +\; y\; 2\; b\; 2\; +\; z\; 2\; c\; 2\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{y\; ^\; \{\; 2\}\}\; \{b\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; =\; 1\}$

и полуоси $a>b>c>0\; \{\backslash \; displaystyle\; a>b>c>0\}$используется вспомогательная сфера с уравнением

$x\; 2\; +\; y\; 2\; +\; z\; 2\; =\; r\; 2.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; =\; r\; ^\; \{2\}\; \backslash .\}$

Радиус сферы должен быть выбран таким, чтобы пересечение с эллипсоидом находилось в двух самолеты через начало координат. Умножение уравнения эллипсоида на $r\; 2\; \{\backslash \; displaystyle\; r\; ^\; \{2\}\}$и вычитание уравнения сферы дает:

$(r\; 2\; a\; 2\; -\; 1)\; x\; 2\; +\; (r\; 2\; б\; 2-1)\; у\; 2\; +\; (г\; 2\; с\; 2-1)\; г\; 2\; знак\; равно\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; x\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\})\; \{b\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; z\; ^\; \{2\}\; =\; 0\; \backslash .\}$

Это уравнение описывает пару плоскостей, если один из трех коэффициентов равен нулю. В случае $r\; =\; a\; \{\backslash \; displaystyle\; \backslash \; r\; =\; a\; \backslash \}$или $r\; =\; c\; \{\backslash \; displaystyle\; \backslash \; r\; =\; c\; \backslash \}$уравнение только выполняется либо по оси x, либо по оси z. Только в случае $r\; =\; b\; \{\backslash \; displaystyle\; \backslash \; r\; =\; b\; \backslash \}$получается пара плоскостей с уравнением

• $(b\; 2\; a\; 2\; -\; 1)\; x\; 2\; +\; (b\; 2\; с\; 2\; -\; 1)\; z\; 2\; знак\; равно\; 0\; \leftrightarrow \; z\; =\; \pm \; caa\; 2\; -\; b\; 2\; b\; 2\; -\; c\; 2\; x,\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; x\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; z\; ^\; \{2\}\; =\; 0\; \backslash \; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; z\; =\; \backslash \; pm\; \{\backslash \; tfrac\; \{c\}\; \{a\}\}\; \{\backslash \; sqrt\; \{\backslash \; tfrac\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\; -c\; ^\; \{2\}\}\; \}\}\; \backslash ;\; x\; \backslash ,\}$

потому что только в этом случае остальные коэффициенты имеют разные знаки (из-за: $a>b>c\; \{\backslash \; displaystyle\; a>b>c\}$).

<189.>Диаграмма дает представление о более общих пересечениях между сферой и эллипсоидом и выделяет исключительный круговой случай (синий).

Если значения полуосей приближаются, два пучка плоскостей (и кружки). Для $a\; =\; b\; \{\backslash \; displaystyle\; a\; =\; b\}$al l плоскости ортогональны оси z (оси вращения).

Доказательство свойства (P): . Вращение эллипсоида вокруг оси y так, чтобы одна из двух окружностей (синяя) лежала в плоскости xy, приводит к новому уравнению эллипсоида:

$A\; Икс\; 2\; +\; B\; Y\; 2\; +\; C\; Z\; 2\; +\; D\; xz\; =\; E\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; By\; ^\; \{2\}\; +\; Cz\; ^\; \{2\}\; +\; D\; \{\backslash \; color\; \{red\}\; xz\}\; =\; E\; \}$

Для $z\; =\; 0\; \{\backslash \; displaystyle\; z\; =\; 0\}$получается $A\; x\; 2\; +\; B\; y\; 2\; =\; E\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; By\; ^\; \{\; 2\}\; =\; E\}$, что должно быть уравнением круга. Это верно, только если $A\; =\; B\; \ne \; 0,\; E>0\; \{\backslash \; displaystyle\; A\; =\; B\; \backslash \; neq\; 0,\; \backslash \; E>0\}$. Пересечение эллипсоида плоскостью с уравнением z <0156>z = {\ displaystyle z = z_ {0}}, (параллельно плоскости xy) имеет уравнение

$A\; (x\; 2\; +\; y\; 2)\; +\; D\; z\; 0\; x\; =\; E\; -\; C\; z\; 0\; 2\; \{\backslash \; displaystyle\; A\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; +\; Dz\_\; \{0\}\; x\; =\; E-Cz\_\; \{0\}\; ^\; \{2\}\}$.

Это уравнение описывает круг, точку или пустое пространство. Центр и радиус круга можно найти как , завершив квадрат.

гиперболоид одного листа

Для гиперболоида одного листа с уравнением

$x\; 2\; a\; 2\; +\; y\; 2\; b\; 2\; -\; z\; 2\; c\; 2\; =\; 1,\; a>b,\; c>0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\; \backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; =\; 1\; \backslash ,\; \backslash \; quad\; a>b\; \backslash ,\; c>0\; \}$

аналогично получается для пересечения со сферой $x\; 2\; +\; y\; 2\; +\; z\; 2\; =\; r\; 2\; \{\backslash \; displaystyle\; \backslash \; x\; ^\; \{2\; \}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; =\; r\; ^\; \{2\}\; \backslash \}$уравнение

$(r\; 2\; a\; 2\; -\; 1)\; x\; 2\; +\; (r\; 2\; b\; 2\; -\; 1)\; у\; 2\; -\; (г\; 2\; с\; 2\; +\; 1)\; г\; 2\; знак\; равно\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; x\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\})\; \{b\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; +\; 1\; \backslash \; right)\; \backslash ;\; z\; ^\; \{2\}\; =\; 0\; \backslash .\}$

Только для $r\; =\; a\; \{\backslash \; displaystyle\; \backslash \; r\; =\; a\; \backslash \}$получается пара плоскостей:

$(a\; 2\; b\; 2\; -\; 1)\; y\; 2\; -\; (a\; 2\; c\; 2\; +\; 1)\; z\; 2\; знак\; равно\; 0\; \leftrightarrow \; z\; =\; \pm \; cba\; 2\; -\; b\; 2\; a\; 2\; +\; c\; 2\; y,\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; +\; 1\; \backslash \; right)\; \backslash ;\; z\; ^\; \{2\}\; =\; 0\; \backslash \; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; z\; =\; \backslash \; pm\; \{\backslash \; frac\; \{c\}\; \{b\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\; \{a\; ^\; \{\; 2\}\; +\; c\; ^\; \{2\}\}\}\}\; \backslash ;\; y\; \backslash ,\; \backslash \}$

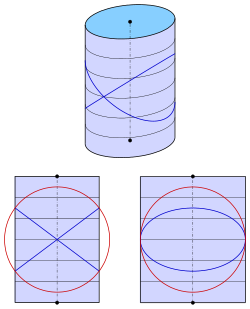
эллиптический цилиндр

Для эллиптического цилиндра с уравнением

$x\; 2\; a\; 2\; +\; Y\; 2\; b\; 2\; =\; 1,\; a>b,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\; \}\}\; =\; 1\; \backslash ,\; \backslash \; quad\; a>b\; \backslash ,\}$

получается уравнение

$(r\; 2\; a\; 2\; -\; 1)\; x\; 2\; +\; (r\; 2\; b\; 2\; -\; 1)\; y\; 2\; -\; z\; 2\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; x\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\})\; \{b\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; -z\; ^\; \{2\}\; =\; 0\; \backslash .\}$

Только для $r\; =\; a\; \{\backslash \; displaystyle\; \backslash \; r\; =\; a\; \backslash \; \}$получается пара плоскостей:

$(a\; 2\; b\; 2\; -\; 1)\; y\; 2\; -\; z\; 2\; =\; 0\; \leftrightarrow \; z\; =\; \pm \; a\; 2\; -\; b\; 2\; by.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; -z\; ^\; \{2\}\; =\; 0\; \backslash \; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; z\; =\; \backslash \; pm\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\}\; \{b\}\}\; \backslash ;\; y\; \backslash .\; \backslash \}$

эллиптический параболоид

Для эллиптический параболоид с уравнением

выбирается сфера, содержащая вершину (начало координат) и с центром на оси (ось z):

$Икс\; 2\; +\; Y\; 2\; +\; (Z\; -\; R)\; 2\; знак\; равно\; R\; 2\; \leftrightarrow \; Икс\; 2\; +\; Y\; 2\; +\; Z\; 2\; -\; 2\; RZ\; =\; 0.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (zr)\; ^\; \{2\}\; =\; r\; ^\; \{2\}\; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\; \}\; -2rz\; =\; 0\; \backslash .\}$

После исключения линейных частей получается уравнение

$(2\; ra\; -\; 1)\; x\; 2\; +\; (2\; rb\; -\; 1)\; y\; 2\; -\; z\; 2\; =\; 0.\; \{\backslash \; displaystyle\; (2ra-1)\; \backslash ;\; x\; ^\; \{2\}\; +\; (2rb-1)\; \backslash ;\; y\; ^\; \{2\}\; -z\; ^\; \{2\}\; =\; 0\; \backslash .\}$

Только для $r\; =\; 1\; 2\; a\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; tfrac\; \{1\}\; \{2a\}\}\}$получается пара плоскостей:

$(ba\; -\; 1)\; y\; 2\; -\; z\; 2\; =\; 0\; \leftrightarrow \; z\; =\; \pm \; б\; -\; ай.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{b\}\; \{a\}\}\; -\; 1\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; -z\; ^\; \{2\}\; =\; 0\; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; z\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{\; \backslash \; frac\; \{ba\}\; \{a\}\}\}\; \backslash ;\; y\; \backslash .\; \backslash \}$

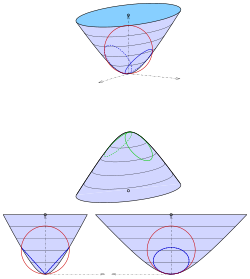
эллиптический гиперболоид из двух листов

гиперболоид из двух листов с уравнением

$-\; x\; 2\; a\; 2\; -\; y\; 2\; b\; 2\; +\; z\; 2\; c\; 2\; =\; 1,\; a>b,\; c>0,\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; =\; 1\; \backslash ,\; \backslash \; quad\; a>b\; \backslash ,\; \backslash \; c>0\; \backslash ,\}$

сначала сдвигается так, что одна вершина является исходной точкой (s. диаграмма):

$-\; x\; 2\; a\; 2\; -\; y\; 2\; b\; 2\; +\; (z\; +\; c)\; 2\; c\; 2\; знак\; равно\; 1\; \leftrightarrow \; -\; x\; 2\; a\; 2\; -\; y\; 2\; b\; 2\; +\; z\; 2\; c\; 2\; +\; 2\; zc\; =\; 0.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\; \}\; -\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{(z\; +\; c)\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; =\; 1\; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; \backslash \; -\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{z\; ^\; \{2\}\; \}\; \{c\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{2z\}\; \{c\}\}\; =\; 0\; \backslash .\}$

Аналогично В случае параболоида выбирается сфера, содержащая начало координат с центром на оси z:

$x\; 2\; +\; y\; 2\; +\; (z\; -\; r)\; 2\; =\; r\; 2\; \leftrightarrow \; x\; 2\; +\; y\; 2\; +\; z\; 2\; -\; 2\; zr\; =\; 0.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (zr)\; ^\; \{2\}\; =\; r\; ^\; \{2\}\; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\; \}\; -2zr\; =\; 0\; \backslash .\}$

После исключения линейных частей получаем уравнение

$(-\; ra\; 2\; +\; 1\; c)\; x\; 2\; +\; (-\; rb\; 2\; +\; 1\; c)\; y\; 2\; +\; (rc\; 2\; +\; 1\; в)\; z\; 2\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (-\; \{\backslash \; frac\; \{r\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \backslash \; right)\; \backslash ;\; x\; ^\; \{2\}\; +\; \backslash \; left\; (-\; \{\backslash \; frac\; \{r\}\; \{b\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{r\}\; \{c\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \backslash \; right)\; z\; ^\; \{2\}\; =\; 0\; \backslash .\}$

Только для $r\; =\; a\; 2\; c\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; tfrac\; \{a\; ^\; \{2\; \}\}\; \{c\}\}\}$получается пара плоскостей:

$(-\; a\; 2\; b\; 2\; c\; +\; 1\; c)\; y\; 2\; +\; (a\; 2\; c\; 3\; +\; 1\; c)\; z\; 2\; =\; 0\; \leftrightarrow \; z\; знак\; равно\; \pm \; cba\; 2\; -\; Ь\; 2\; а\; 2\; +\; с\; 2\; у.\; \{\backslash \; displaystyle\; \backslash \; left\; (-\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\; c\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \backslash \; right)\; \backslash ;\; y\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{c\; ^\; \{3\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \backslash \; right)\; \backslash ;\; z\; ^\; \{2\}\; =\; 0\; \backslash \; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; z\; =\; \backslash \; pm\; \{\backslash \; frac\; \{c\}\; \{b\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\; +\; c\; ^\; \{2\}\}\}\}\; \backslash ;\; y\; \backslash .\}$

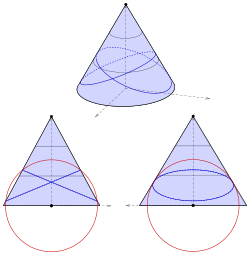
эллиптический конус

Эллиптический конус с уравнением

$x\; 2\; a\; 2\; +\; y\; 2\; b\; 2\; -\; z\; 2\; =\; 0,\; a>b,\; \{\; \backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; -\; z\; ^\; \{2\}\; =\; 0\; \backslash ,\; \backslash \; quad\; a>b\; \backslash ,\}$

сдвигается так, что вершина не является исходной точкой (s. диаграмма):

$x\; 2\; a\; 2\; +\; y\; 2\; b\; 2\; -\; (z\; -\; 1)\; 2\; =\; 0\; \leftrightarrow \; x\; 2\; a\; 2\; +\; y\; 2\; b\; 2\; -\; z\; 2\; +\; 2\; z\; =\; 1.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{\; b\; ^\; \{2\}\}\}\; -\; (z-1)\; ^\; \{2\}\; =\; 0\; \backslash \; quad\; \backslash \; leftrightarrow\; \backslash \; quad\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; -\; z\; ^\; \{2\}\; +\; 2z\; =\; 1.\}$

Теперь подходит сфера с центром в начале координат:

$x\; 2\; +\; y\; 2\; +\; z\; 2\; =\; г\; 2.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; =\; r\; ^\; \{2\}\; \backslash .\}$

Исключение $x\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\}$дает:

$(a\; 2\; b\; 2-1)\; y\; 2\; -\; (1\; +\; a\; 2)\; z\; 2\; +\; 2\; a\; 2\; z\; =\; a\; 2\; -\; r\; 2.\; \{\backslash \; displaystyle\; (\{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; -\; 1)\; \backslash ;\; y\; ^\; \{2\}\; -\; (1\; +\; a\; ^\; \{2\})\; \backslash ;\; z\; ^\; \{2\}\; +\; 2a\; ^\; \{2\}\; z\; =\; a\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash .\}$

В этом случае завершение квадрата дает:

$a\; 2\; -\; b\; 2\; b\; 2\; y\; 2\; -\; (1\; +\; a\; 2)\; (г\; -\; а\; 2\; 1\; +\; а\; 2)\; 2\; =\; а\; 2\; -\; а\; 4\; 1\; +\; а\; 2\; -\; г\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; \backslash ;\; y\; ^\; \{2\}\; -\; (1\; +\; a\; ^\; \{2\})\; \backslash \; left\; (z-\; \{\; \backslash \; frac\; \{a\; ^\; \{2\}\}\; \{1\; +\; a\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; a\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{a\; ^\; \{4\}\}\; \{1\; +\; a\; ^\; \{2\; \}\}\}\; -\; r\; ^\; \{2\}\; \backslash .\}$

Чтобы получить уравнение пары плоскостей, правая часть уравнения должна быть равна нулю, что верно для $r\; =\; a\; 1\; +\; а\; 2.\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; tfrac\; \{a\}\; \{\backslash \; sqrt\; \{1\; +\; a\; ^\; \{2\}\}\}\}\; \backslash .\}$Решение для z дает:

$z\; =\; a\; 2\; 1\; +\; a\; 2\; \pm \; 1\; ba\; 2\; -\; b\; 2\; 1\; +\; a\; 2\; y.\; \{\backslash \; displaystyle\; z\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{1\; +\; a\; ^\; \{2\}\}\}\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{b\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{a\; ^\; \{2\}\; -\; b\; ^\; \{2\}\}\; \{1\; +\; a\; ^\; \{2\}\}\}\}\; \backslash ;\; y\; \backslash .\}$

• H. Ф. Бейкер: Принципы геометрии, Том 3, Cambridge University Press, 2010, ISBN 978-1-108-01779-4.
• D. М. Ю. Соммервилл: Аналитическая геометрия трех измерений, Cambridge University Press, 1959, ISBN 978-1-316-60190-7, p. 204.
• К. П. Гротемейер: Аналитическая геометрия. Göschen-Verlag, 1962, стр. 143.
• Х. Scheid, W. Schwarz: Elemente der Linearen Algebra und der Analysis. Spektrum, Heidelberg, 2009, ISBN 978-3-8274-1971-2, стр. 132.

1. ^W. Х. Вестфаль: Physikalisches Wörterbuch: Zwei Teile in Einem Band. Springer-Verlag, 1952, ISBN 978-3-662-12707-0, стр. 350.
2. ^Х. Tertsch: Die Festigkeitserscheinungen der Kristalle. Springer-Verlag, Wien, 1949, ISBN 978-3-211-80120-8, p. 87.
3. ^Г. Мазинг: Lehrbuch der Allgemeinen Metallkunde. Springer-Verlag, Берлин, 1950, ISBN 978-3-642-52-993-1, p. 355.

• H. Винер, П. Трейтлейн: Модели трехосного эллипсоида и эллиптического параболоида с использованием круговых сечений (см. Стр. 15) [1pting (PDF).