График нулевого полюса

В математике, обработка сигналов и теория управления, график полюс – ноль - это графическое представление рациональной передаточной функции в комплексной плоскости, которая помогает для передачи определенных свойств системы, таких как:

• Стабильность
• Причинная система / антикаузальная система
• Область конвергенции (ROC)
• Минимальная фаза / не минимальная фаза

График нулевого полюса показывает расположение в комплексной плоскости полюсов и нулей передаточной функции динамической системы , такой как контроллер, компенсатор, датчик, эквалайзер, фильтр, или канал связи. По соглашению, полюса системы обозначены на графике знаком X, а нули обозначены кружком или O.

График полюс-нуль может представлять либо непрерывное время (CT), либо система с дискретным временем (ДТ). Для системы CT плоскость, в которой появляются полюса и нули, является плоскостью s преобразования Лапласа. В этом контексте параметр s представляет комплексную угловую частоту, которая является областью передаточной функции CT. Для системы DT плоскость - это плоскость z, где z представляет область Z-преобразования.

• 1 Системы непрерывного времени
  • 1.1 Полюса и нули
  • 1.2 Область сходимость
  • 1.3 Пример
• 2 Системы с дискретным временем
  • 2.1 Полюса и нули
  • 2.2 Область сходимости
  • 2.3 Пример
• 3 См. также
• 4 Библиография

В общем, рациональная передаточная функция для непрерывной системы LTI имеет вид:

$H\; (s)\; =\; B\; (s)\; A\; (s)\; =\; \sum \; m\; =\; 0\; M\; bmsms\; N\; +\; \sum \; n\; =\; 0\; N\; -\; 1\; ansn\; =\; b\; 0\; +\; b\; 1\; s\; +\; b\; 2\; s\; 2\; +\; \cdots \; +\; b\; M\; s\; M\; a\; 0\; +\; a\; 1\; s\; +\; a\; 2\; s\; 2\; +\; \cdots \; +\; a\; (N\; -\; 1)\; s\; (N\; -\; 1)\; +\; s\; N\; \{\backslash \; Displaystyle\; H\; (s)\; =\; \{\backslash \; frac\; \{B\; (s)\}\; \{A\; (s)\}\}\; =\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{\; m\; =\; 0\}\; ^\; \{M\}\; \{b\_\; \{m\}\; s\; ^\; \{m\}\}\; \backslash \; over\; s\; ^\; \{N\}\; +\; \backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{N-1\}\; \{a\_\; \{n\}\; s\; ^\; \{n\}\}\}\; =\; \{\backslash \; frac\; \{b\_\; \{0\}\; +\; b\_\; \{1\}\; s\; +\; b\_\; \{2\}\; s\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; b\_\; \{M\}\; s\; ^\; \{M\}\}\; \{a\_\; \{0\}\; +\; a\_\; \{1\}\; s\; +\; a\_\; \{2\}\; s\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; a\; \_\; \{(N-1)\}\; s\; ^\; \{(N-1)\}\; +\; s\; ^\; \{N\}\}\}\}$

где

• $B\; \{\backslash \; displaystyle\; B\}$и $A\; \{\backslash \; displaystyle\; A\}$являются полиномиальными mials в $s\; \{\backslash \; displaystyle\; s\}$,
• $M\; \{\backslash \; displaystyle\; M\}$- порядок полинома числителя,
• $bm\; \{\backslash \; displaystyle\; b\_\; \{m\}\}$- m-й коэффициент полинома числителя,
• $N\; \{\backslash \; displaystyle\; N\}$- порядок полинома знаменателя, а
• $\{\backslash \; displaystyle\; a\_\; \{n\}\}$- n-й коэффициент полинома знаменателя.

Либо M, либо N, либо оба могут быть равны нулю, но в реальных системах должно быть так, что $M\; \le \; N\; \{\backslash \; displaystyle\; M\; \backslash \; leq\; N\}$; в противном случае усиление было бы неограниченным на высоких частотах.

Полюсы и нули

• нули системы являются корнями полинома числителя:

$s\; =\; \{\beta \; m\; |\; m\; \in \; 1,\dots \; M\}\; \{\backslash \; displaystyle\; s\; =\; \backslash \; \{\backslash \; beta\; \_\; \{m\}\; |\; m\; \backslash \; in\; 1,\; \backslash \; ldots\; M\; \backslash \}\}$такой, что $B\; (s)\; |\; s\; =\; \beta \; m\; =\; 0\; \{\backslash \; displaystyle\; B\; (s)\; |\; \_\; \{s\; =\; \backslash \; beta\; \_\; \{m\}\}\; =\; 0\}$

• полюса системы являются корнями полинома знаменателя:

$s\; =\; \{\alpha \; п\; |\; n\; \in \; 1,\dots \; N\}\; \{\backslash \; displaystyle\; s\; =\; \backslash \; \{\backslash \; alpha\; \_\; \{n\}\; |\; n\; \backslash \; in\; 1,\; \backslash \; ldots\; N\; \backslash \}\}$такой, что $A\; (s)\; |\; s\; =\; \alpha \; N\; =\; 0\; \{\backslash \; displaystyle\; A\; (s)\; |\; \_\; \{s\; =\; \backslash \; alpha\; \_\; \{n\}\}\; =\; 0\}$.

Область конвергенции

Область конвергенции (ROC) для данной передаточной функции CT представляет собой полуплоскость или вертикальную полосу, каждая из которых не содержит полюсов. В общем, ROC не уникален, и конкретный ROC в каждом конкретном случае зависит от того, является ли система причинной или антипричинной.

• Если ROC включает в себя мнимую ось, то система стабильна с ограниченным входом и ограниченным выходом (BIBO).
• Если ROC простирается вправо от полюса с наибольшим действительная часть (но не на бесконечности), тогда система является причинной.
• Если ROC простирается влево от полюса с наименьшей действительной частью (но не на отрицательной бесконечности), то система является антипричинной.

ROC обычно выбирается с учетом мнимой оси, поскольку для большинства практических систем важно иметь стабильность BIBO.

Пример

$H\; (s)\; =\; 25\; с\; 2\; +\; 6\; s\; +\; 25\; \{\backslash \; displaystyle\; H\; (s)\; =\; \{25\; \backslash \; over\; s\; ^\; \{2\}\; +\; 6s\; +\; 25\}\}$

Эта система не имеет (конечных) нулей и двух полюсов:

$s\; =\; \alpha \; 1\; Знак\; равно\; -\; 3\; +\; 4\; j\; \{\backslash \; displaystyle\; s\; =\; \backslash \; alpha\; \_\; \{1\}\; =\; -\; 3\; +\; 4j\}$

и

$s\; =\; \alpha \; 2\; =\; -\; 3\; -\; 4\; j\; \{\backslash \; displaystyle\; s\; =\; \backslash \; alpha\; \_\; \{2\; \}\; =\; -\; 3-4j\}$

График «полюс-ноль» будет выглядеть следующим образом:

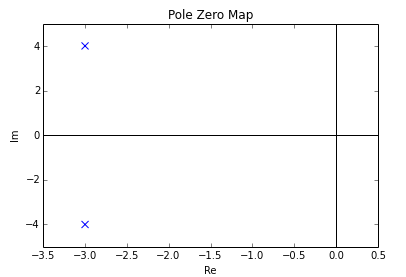
Обратите внимание, что эти два полюса являются комплексно сопряженными, что является необходимым и достаточным условием для получения действительных коэффициентов в разные иальное уравнение, представляющее систему.

В общем случае рациональная передаточная функция для системы с дискретным временем LTI имеет вид:

$H\; (z)\; =\; P\; (\; z)\; Q\; (z)\; =\; \sum \; m\; =\; 0\; M\; bmz\; -\; m\; 1\; +\; \sum \; n\; =\; 1\; N\; anz\; -\; n\; =\; b\; 0\; +\; b\; 1\; z\; -\; 1\; +\; b\; 2\; z\; -\; 2\; \cdots \; +\; b\; M\; z\; -\; M\; 1\; +\; a\; 1\; Z\; -\; 1\; +\; a\; 2\; Z\; -\; 2\; \cdots \; +\; a\; N\; Z\; -\; N\; \{\backslash \; Displaystyle\; H\; (z)\; =\; \{\backslash \; frac\; \{P\; (z)\}\; \{Q\; (z)\}\}\; =\; \{\backslash \; frac\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{м\; =\; 0\}\; ^\; \{M\}\; \{b\_\; \{m\}\; z\; ^\; \{-\; m\}\}\}\; \{1+\; \backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; \{a\_\; \{n\}\; z\; ^\; \{-\; n\; \}\}\}\}\; =\; \{\backslash \; frac\; \{b\_\; \{0\}\; +\; b\_\; \{1\}\; z\; ^\; \{-\; 1\}\; +\; b\_\; \{2\}\; z\; ^\; \{-\; 2\}\; \backslash \; cdots\; +\; b\_\; \{M\}\; z\; ^\; \{-\; M\}\}\; \{\; 1\; +\; a\_\; \{1\}\; z\; ^\; \{-\; 1\}\; +\; a\_\; \{2\}\; z\; ^\; \{-\; 2\}\; \backslash \; cdots\; +\; a\_\; \{N\}\; z\; ^\; \{-\; N\}\}\}\}$

где

• $M\; \{\backslash \; displaystyle\; M\}$- это порядок полинома числителя,
• $bm\; \{\backslash \; displaystyle\; b\_\; \{m\}\}$- m-й коэффициент полинома числителя,
• $N\; \{\; \backslash \; displaystyle\; N\}$- это порядок полинома знаменателя, а
• $an\; \{\backslash \; displaystyle\; a\_\; \{n\}\}$- n-й коэффициент полинома знаменателя.

Либо M, либо N, либо оба могут быть равны нулю.

Полюсы и нули

• $z\; =\; \beta \; m\; \{\backslash \; displaystyle\; z\; =\; \backslash \; beta\; \_\; \{m\}\}$такие, что $P\; (z)\; |\; z\; =\; \beta \; m\; =\; 0\; \{\backslash \; displaystyle\; P\; (z)\; |\; \_\; \{z\; =\; \backslash \; beta\; \_\; \{m\}\}\; =\; 0\}$- нули системы
• $z\; =\; \alpha \; N\; \{\backslash \; displaystyle\; z\; =\; \backslash \; alpha\; \_\; \{n\}\}$такой, что $Q\; (z)\; |\; z\; =\; \alpha \; n\; =\; 0\; \{\backslash \; displaystyle\; Q\; (z)\; |\; \_\; \{z\; =\; \backslash \; alpha\; \_\; \{n\}\}\; =\; 0\}$- полюса системы.

Область конвергенции

Область конвергенции (ROC) для данной передаточной функции DT - это диск или кольцевое пространство, не содержащее полюсов. В общем, ROC не уникален, и конкретный ROC в каждом конкретном случае зависит от того, является ли система причинной или антипричинной.

• Если ROC включает в себя единичную окружность, тогда система стабильна с ограниченным входом и ограниченным выходом (BIBO).
• Если ROC выходит наружу от полюса с наибольшим ( но не бесконечной) величины, то система имеет правосторонний импульсный отклик. Если ROC выходит наружу от полюса с наибольшей величиной и нет полюса на бесконечности, тогда система является причинной.
• Если ROC простирается внутрь от полюса с наименьшей (ненулевой) величиной, то система является антипричинной.

ROC обычно выбирается для включения единичного круга, поскольку для большинства практических систем важно иметь стабильность BIBO.

Пример

Если $P\; (\; z)\; \{\backslash \; displaystyle\; P\; (z)\}$и $Q\; (z)\; \{\backslash \; displaystyle\; Q\; (z)\}$полностью разложены на множители, их решение может быть легко отображено в z-плоскость. Например, при следующей передаточной функции:

$H\; (z)\; =\; z\; +\; 2\; z\; 2\; +\; 1\; 4\; \{\backslash \; displaystyle\; H\; (z)\; =\; \{\backslash \; frac\; \{z\; +\; 2\}\; \{z\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{1\}\; \{4\}\}\}\}\}$

Единственный (конечный) ноль расположен в: $z\; =\; -\; 2\; \{\backslash \; displaystyle\; z\; =\; -2\}$, а два полюса расположены по адресу: $z\; =\; \pm \; j\; 2\; \{\backslash \; displaystyle\; z\; =\; \backslash \; pm\; \{\backslash \; frac\; \{j\}\; \{2\}\}\}$, где j - мнимая единица.

График «полюс – ноль» будет иметь вид:

• Корневой локус
• преобразование Лапласа
• Z-преобразование
• Рациональная функция

• Хааг, Майкл (22 июня 2005 г.). «Понимание графиков полюса / нуля на Z-плоскости». OpenStax CNX. Проверено 9 июня 2018 г.
• Эрик В. Вайстейн. "Z-преобразование". MathWorld. Получено 24 января 2010 г.