Helix

Тип гладкой пространственной кривой Правая спираль (cos t, sin t, t) от t = 0 до 4π со стрелками, показывающими направление увеличения t

A спирали (), множественных спиралей или спиралей (), имеет форму штопора или винтовой лестницы. Это тип гладкой пространственной кривой с касательными под постоянным углом к фиксированной оси. Спирали важны в биологии, поскольку молекула ДНК формируется как две переплетенные спирали, и многие белки имеют спиральные субструктуры, известные как альфа-спирали. Слово спираль происходит от греческого слова ἕλιξ, «скрученный, изогнутый». «Заполненная» спираль - например, «спиральная» (спиральная) наклонная поверхность - называется геликоидом.

• 1 Типы
• 2 Математическое описание
  • 2.1 Длина дуги, кривизна и кручение
• 3 Примеры
• 4 См. также
• 5 Ссылки

Спирали могут быть правосторонними или левосторонними. Если при взгляде вдоль оси спирали вращательное движение по часовой стрелке отодвигает спираль от наблюдателя, то это называется правой спиралью; если в сторону наблюдателя, то это левая спираль. Направленность (или хиральность ) - это свойство спирали, а не перспективы: правую спираль нельзя повернуть так, чтобы она выглядела как левосторонняя, если ее не смотреть в зеркало, и наоборот..

Два типа спирали показаны в сравнении . Это показывает две хиральности спиралей. Один левша, а другой правша. В каждой строке сравниваются две спирали с разных точек зрения. Хиральность - это свойство объекта, а не перспективы (угол обзора)

Большинство аппаратных средств резьбы имеют правую спираль. Альфа-спираль в биологии, а также формы A и B ДНК также являются правыми спиралями. Z-форма ДНК является левосторонней.

Шаг шаг спирали - это высота одного полного витка спирали, измеренная параллельно оси спирали.

A двойная спираль состоит из двух (обычно конгруэнтных ) спиралей с одной и той же осью, различающихся перемещением вдоль оси.

A коническая спираль может быть определена как спираль на конической поверхности, причем расстояние до вершины экспоненциально зависит от угла, указывающего направление от оси. Примером могут служить американские горки Corkscrew в парке развлечений Cedar Point.

A круговая спираль, (т.е. спираль с постоянным радиусом) имеет постоянную полосу кривизну и постоянную кручение.

Кривая называется общей спиралью или цилиндрическая спираль, если ее касательная составляет постоянный угол с фиксированной линией в пространстве. Кривая является общей спиралью тогда и только тогда, когда отношение кривизны к кручению является постоянным.

Геометрический шаг - это расстояние, на которое продвинется элемент винта самолета. за один оборот, если бы он двигался по спирали, имеющей угол, равный углу между хордой элемента и плоскостью, перпендикулярной оси воздушного винта.

Кривая называется наклонной спиралью, если ее главная нормаль образует постоянный угол с фиксированной линией в пространстве. Его можно построить, применив преобразование к движущейся системе отсчета общей спирали.

Некоторые кривые, встречающиеся в природе, состоят из множества спиралей разной направленности, соединенных вместе переходами, известными как извращения усиков.

Спираль, составленная из синусоидальных компонентов x и y

В математике спираль - это кривая в 3- мерном пространстве. Следующая параметризация в декартовых координатах определяет конкретную спираль; возможно, самое простое уравнение для одного:

$x\; (t)\; =\; cos\; \; (t),\; \{\backslash \; displaystyle\; x\; (t)\; =\; \backslash \; cos\; (t),\; \backslash ,\}$

$y\; (t)\; =\; sin\; \; (t),\; \{\backslash \; Displaystyle\; у\; (т)\; =\; \backslash \; грех\; (т),\; \backslash ,\}$

$г\; (т)\; =\; т.\; \{\backslash \; displaystyle\; z\; (t)\; =\; t.\; \backslash ,\}$

По мере увеличения параметра t точка (x (t), y (t), z (t)) отслеживает правый спираль с шагом 2π (или наклоном 1) и радиусом 1 вокруг оси z в правой системе координат.

В цилиндрических координатах (r, θ, h) одна и та же спираль параметризуется следующим образом:

$r\; (t)\; =\; 1,\; \{\backslash \; displaystyle\; r\; (t)\; =\; 1,\; \backslash ,\}$

$\theta \; (t)\; знак\; равно\; t,\; \{\backslash \; displaystyle\; \backslash \; theta\; (t)\; =\; t,\; \backslash ,\}$

$h\; (t)\; =\; t.\; \{\backslash \; displaystyle\; h\; (t)\; =\; t.\; \backslash ,\}$

Круговая спираль радиуса a и наклона b / a (или шага 2πb) описывается следующей параметризацией:

$x\; (t)\; =\; a\; cos\; \; (T),\; \{\backslash \; Displaystyle\; х\; (т)\; =\; а\; \backslash \; соз\; (т),\; \backslash ,\}$

$у\; (т)\; =\; грех\; \; (т),\; \{\backslash \; Displaystyle\; у\; (т)\; =\; а\; \backslash \; грех\; (т),\; \backslash ,\}$

$z\; (t)\; =\; bt.\; \{\backslash \; displaystyle\; z\; (t)\; =\; bt.\; \backslash ,\}$

Другой способ математического построения спирали - построить комплексную функцию e как функцию действительного числа x (см. формулу Эйлера ). Значение x, а также действительная и мнимая части значения функции дают этому графику три реальных измерения.

За исключением поворотов, перемещений и изменений масштаба, все правые спирали эквивалентны спирали, определенной выше. Эквивалентная левая спираль может быть построена несколькими способами, самым простым из которых является отрицание любого из компонентов x, y или z.

Длина дуги, кривизна и кручение

Длина круговой спирали с радиусом a и наклоном b / a (или шагом 2πb), выраженная в прямоугольных координатах как

$t\; \mapsto \; (a\; cos\; \; T,\; грех\; \; T,\; bt),\; T\; \in \; [0,\; T]\; \{\backslash \; displaystyle\; t\; \backslash \; mapsto\; (a\; \backslash \; cos\; t,\; a\; \backslash \; sin\; t,\; bt),\; t\; \backslash \; in\; [0,\; T]\}$

равно $T\; \cdot \; a\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; T\; \backslash \; cdot\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}$, его кривизна это $|\; а\; |\; a\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{|\; a\; |\}\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}$и его кручение равно $ба\; 2\; +\; б\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{b\}\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}.\}$Спираль имеет постоянную ненулевую кривизну и кручение.

Спираль - это векторнозначная функция

$r\; =\; a\; cos\; \; ti\; +\; a\; sin\; \; tj\; +\; btk\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; =\; a\; \backslash \; cos\; t\; \backslash \; mathbf\; \{i\}\; +\; a\; \backslash \; sin\; t\; \backslash \; mathbf\; \{j\}\; +\; bt\; \backslash \; mathbf\; \{k\}\}$

$v\; =\; -\; грех\; \; ti\; +\; a\; cos\; \; tj\; +\; bk\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; -a\; \backslash \; sin\; t\; \backslash \; mathbf\; \{\; я\}\; +\; a\; \backslash \; соз\; t\; \backslash \; mathbf\; \{j\}\; +\; b\; \backslash \; mathbf\; \{k\}\}$

$a\; =\; -\; a\; cos\; \; ti\; -\; грех\; \; tj\; +\; 0\; k\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{a\}\; =\; -a\; \backslash \; cos\; t\; \backslash \; mathbf\; \{i\}\; -a\; \backslash \; sin\; t\; \backslash \; mathbf\; \{j\}\; +0\; \backslash \; mathbf\; \{k\}\}$

$|\; v\; |\; Знак\; равно\; (-\; грех\; \; T)\; 2\; +\; (a\; соз\; \; t)\; 2\; +\; b\; 2\; =\; a\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{v\}\; |\; =\; \{\backslash \; sqrt\; \{(-a\; \backslash \; sin\; t)\; ^\; \{\; 2\}\; +\; (a\; \backslash \; cos\; t)\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\; =\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}$

$|\; а\; |\; Знак\; равно\; (-\; грех\; \; T)\; 2\; +\; (a\; соз\; \; t)\; 2\; знак\; равно\; a\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{a\}\; |\; =\; \{\backslash \; sqrt\; \{(-a\; \backslash \; sin\; t)\; ^\; \{2\}\; +\; (a\; \backslash \; cos\; t)\; ^\; \{2\}\}\}\; =\; a\}$

$s\; (t)\; =\; \int \; 0\; ta\; 2\; +\; b\; 2\; d\; \tau \; =\; a\; 2\; +\; b\; 2\; t\; \{\backslash \; displaystyle\; s\; (t)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{t\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\; d\; \backslash \; tau\; =\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\; t\}$

Таким образом, спираль может быть повторно параметризованным как функция от $s\; \{\backslash \; displaystyle\; s\}$, который должен быть единичной скоростью:

$r\; (s)\; =\; a\; cos\; \; sa\; 2\; +\; b\; 2\; i\; +\; a\; sin\; \; sa\; 2\; +\; b\; 2\; j\; +\; bsa\; 2\; +\; b\; 2\; к\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; (s)\; =\; a\; \backslash \; cos\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\; \}\}\; \backslash \; mathbf\; \{i\}\; +\; a\; \backslash \; sin\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{j\}\; +\; \{\backslash \; frac\; \{bs\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{k\}\}$

Единичный касательный вектор равен

$drds\; =\; T\; =\; -\; aa\; 2\; +\; b\; 2\; sin\; \; sa\; 2\; +\; b\; 2\; i\; +\; aa\; 2\; +\; b\; 2\; соз\; \; sa\; 2\; +\; b\; 2\; j\; +\; ba\; 2\; +\; b\; 2\; k\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{ds\}\}\; =\; \backslash \; mathbf\; \{T\}\; =\; \{\backslash \; frac\; \{\; -a\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; sin\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{\; i\}\; +\; \{\backslash \; frac\; \{a\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; cos\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\; \}\}\}\; \backslash \; mathbf\; \{j\}\; +\; \{\backslash \; frac\; \{b\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{k\}\}$

Вектор нормали равен

$d\; T\; ds\; =\; \kappa \; N\; =\; -\; aa\; 2\; +\; b\; 2\; cos\; \; sa\; 2\; +\; b\; 2\; i\; +\; -\; aa\; 2\; +\; b\; 2\; грех\; \; sa\; 2\; +\; b\; 2\; J\; +\; 0\; к\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{T\}\}\; \{ds\}\}\; =\; \backslash \; kappa\; \backslash \; mathbf\; \{N\}\; =\; \{\backslash \; frac\; \{-\; a\}\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\; \backslash \; cos\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{i\}\; +\; \{\backslash \; frac\; \{-a\}\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\; \backslash \; sin\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{j\}\; +0\; \backslash \; mathbf\; \{k\}\}$

Его кривизна $|\; d\; T\; d\; s\; |\; =\; \kappa \; =\; |\; а\; |\; a\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; \{\backslash \; bigg\; |\}\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{T\}\}\; \{ds\}\}\; \{\backslash \; bigg\; |\}\; =\; \backslash \; kappa\; =\; \{\backslash \; frac\; \{|\; a\; |\}\; \{a\; ^\; \{2\; \}\; +\; b\; ^\; \{2\}\}\}\}$.

Единичный вектор нормали равен

$N\; =\; -\; cos\; \; sa\; 2\; +\; b\; 2\; i\; -\; sin\; \; sa\; 2\; +\; b\; 2\; j\; +\; 0\; k\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\; N\}\; =\; -\; \backslash \; cos\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{i\}\; -\; \backslash \; sin\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{j\}\; +0\; \backslash \; mathbf\; \{k\}\}$

Вектор бинормали равен

$B\; =\; T\; \times \; N\; =\; 1\; a\; 2\; +\; b\; 2\; [b\; sin\; \; sa\; 2\; +\; b\; 2\; я\; -\; b\; соз\; \; sa\; 2\; +\; b\; 2\; j\; +\; ak]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; =\; \backslash \; mathbf\; \{T\}\; \backslash \; times\; \backslash \; mathbf\; \{N\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \{\backslash \; bigg\; [\}\; b\; \backslash \; sin\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{i\}\; -b\; \backslash \; cos\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{j\}\; +\; a\; \backslash \; mathbf\; \{k\}\; \{\backslash \; bigg]\}\}$

. $d\; B\; ds\; =\; 1\; a\; 2\; +\; b\; 2\; [b\; cos\; \; sa\; 2\; +\; b\; 2\; i\; +\; b\; sin\; \; sa\; 2\; +\; b\; 2\; j\; +\; 0\; k]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{B\}\}\; \{ds\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\; \{\backslash \; bigg\; [\}\; b\; \backslash \; cos\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{i\}\; +\; b\; \backslash \; sin\; \{\backslash \; frac\; \{s\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\; \backslash \; mathbf\; \{j\}\; +0\; \backslash \; mathbf\; \{\; k\}\; \{\backslash \; bigg]\}\}$

Его кручение $\tau \; =\; |\; d\; B\; d\; s\; |\; =\; ba\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \{\backslash \; bigg\; |\}\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{B\}\}\; \{ds\}\}\; \{\backslash \; bigg\; |\}\; =\; \{\backslash \; frac\; \{b\}\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}$.

В музыке пространство тона часто моделируется спиралями или двойными спиралями, чаще всего выходящими из круг, такой как круг квинтов, чтобы представить октавную эквивалентность.

• 

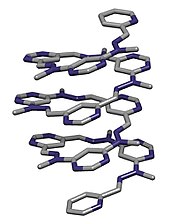
  Кристаллическую структуру свернутой молекулярной спирали, сообщенную Lehn et al. al. в Helv. Чим. Acta., 2003, 86, 1598–1624.

• 

  Естественная левая спираль, созданная альпинистом растением

• 

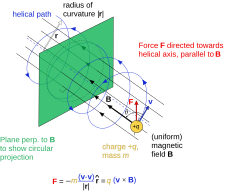
  Заряженная частица в однородном магнитном поле, движущаяся по спиральной траектории

• 

  Винтовая пружина

• Альфа-спираль
• Спираль Бурдейка – Кокстера
• Коллагеновая спираль
• Спиральная симметрия
• Hemihelix
• Угол спирали
• Поверхность морской раковины
• Соленоид
• Superhelix
• Тройная спираль

<https://www.merriam-webster.com/dictionary/geometrical%20pitch