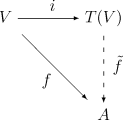Тензорная алгебра

редактировать

Универсальная конструкция в полилинейной алгебре

В математике тензорная алгебра векторного пространства V, обозначаемого T (V) или T (V), является алгеброй тензоров на V (любого ранга) с умножение - тензорное произведение . Это свободная алгебра на V, в том смысле, что она сопряжена слева с забывчивым функтором из алгебр в векторные пространства: это «самый общий» алгебра, содержащая V, в смысле соответствующего универсального свойства (см. ниже).

Тензорная алгебра важна, потому что многие другие алгебры возникают как факторалгебры алгебры T (V). К ним относятся внешняя алгебра, симметрическая алгебра, алгебры Клиффорда, алгебра Вейля и универсальные обертывающие алгебры.

Тензорная алгебра также имеет две структуры коалгебры ; один простой, который не делает его биалгеброй, но приводит к концепции cofree коалгебры, и более сложный, который дает биалгебру, и может быть расширен давая антипод для создания структуры алгебры Хопфа.

Примечание. В этой статье все алгебры считаются унитальными и ассоциативными. Единица явно требуется для определения сопродукта.

Содержание

1 Конструкция
2 Присоединение и универсальное свойство
3 Некоммутативные многочлены
4 Факторы
5 Коалгебра
- 5.1 Копродукт
- 5.2 Counit
6 Биалгебра
- 6.1 Умножение
- 6.2 Единица
- 6.3 Совместимость
7 Алгебра Хопфа
- 7.1 Совместимость
8 Совместная совместная коалгебра
9 См. Также
10 Ссылки

Конструкция

Пусть V будет векторным пространством над полем K. Для любого неотрицательного целого k мы определяем k-ю тензорную степень числа V как тензорное произведение числа V на себя k раз:

T k V = V ⊗ k = V ⊗ V ⊗ ⋯ ⊗ V. {\ displaystyle T ^ {k} V = V ^ {\ otimes k} = V \ otimes V \ otimes \ cdots \ otimes V.}

T^kV = V^{\otimes k} = V\otimes V \otimes \cdots \otimes V.

То есть TV состоит из всех тензоров на V порядка к. По соглашению TV - это основное поле K (как одномерное векторное пространство над собой).

Затем мы строим T (V) как прямую сумму TV для k = 0,1,2,…

T (V) = ⨁ k = 0 ∞ T k V = K ⊕ V ⊕ (V ⊗ V) ⊕ (V ⊗ V ⊗ V) ⊕ ⋯. {\ Displaystyle T (V) = \ bigoplus _ {k = 0} ^ {\ infty} T ^ {k} V = K \ oplus V \ oplus (V \ otimes V) \ oplus (V \ otimes V \ otimes V) \ oplus \ cdots.}

T (V) = \ bigoplus_ {k = 0} ^ \ infty T ^ kV = K \ oplus V \ oplus (V \ otimes V) \ oplus (V \ otimes V \ otimes V) \ oplus \ cdots.

Умножение в T (V) определяется каноническим изоморфизмом

T k V ⊗ T ℓ V → T k + ℓ V {\ displaystyle T ^ {k} V \ otimes T ^ {\ ell} V \ to T ^ {k + \ ell} V}

T ^ kV \ otimes T ^ \ ell V \ to T ^ {k + \ ell} V

, заданное тензорным произведением, которое затем распространяется по линейности на все T (V). Из этого правила умножения следует, что тензорная алгебра T (V) естественно является градуированной алгеброй с TV, служащей подпространством степени k. Эту оценку можно расширить до оценки Z, добавив подпространства $T k V = {0} {\ displaystyle T ^ {k} V = \ {0 \}}$ $T ^ {k} V = \ {0 \}$ для отрицательных целых чисел k.

Конструкция прямо обобщается на тензорную алгебру любого модуля M над коммутативным кольцом. Если R является некоммутативным кольцом, все еще можно выполнить построение для любого R-R бимодуля M. (Это не работает для обычных R-модулей, потому что повторяющиеся тензорные произведения не могут быть сформированы.)

Сочетание и универсальное свойство

Тензорная алгебра T (V) также называется свободная алгебра на векторном пространстве V и является функториальной. Как и другие свободные конструкции, функтор T сопряжен слева с некоторым забывающим функтором. В данном случае это функтор, который отправляет каждую K-алгебру в соответствующее векторное пространство.

Явно тензорная алгебра удовлетворяет следующему универсальному свойству, которое формально выражает утверждение, что это наиболее общая алгебра, содержащая V:

Любое линейное преобразование f: V → A из V в алгебру A над K может быть однозначно расширен до гомоморфизма алгебр из T (V) в A, как показано следующей коммутативной диаграммой :

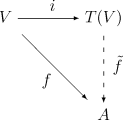
Универсальное свойство тензорной алгебры

Здесь i есть каноническое включение V в T (V) (единица присоединения). Фактически можно определить тензорную алгебру T (V) как единственную алгебру, удовлетворяющую этому свойству (в частности, она единственна до единственного изоморфизма), но все же необходимо доказать, что объект, удовлетворяющий этому свойству собственность существует.

Вышеупомянутое универсальное свойство показывает, что построение тензорной алгебры является функториальным по природе. То есть T является функтором от K-Vect, категории векторных пространств над K, до K-Alg, категория K-алгебр. Функториальность T означает, что любое линейное отображение между K-векторными пространствами U и W однозначно продолжается до гомоморфизма K-алгебр из T (U) в T (W).

Некоммутативные многочлены

Если V имеет конечную размерность n, другой способ рассмотрения тензорной алгебры - это «алгебра многочленов над K от n некоммутирующих переменных». Если мы возьмем базисные векторы для V, они станут некоммутирующими переменными (или неопределенными ) в T (V), без ограничений, кроме ассоциативности, закон распределения и K-линейность.

Обратите внимание, что алгебра многочленов на V не $T (V) {\ displaystyle T (V)}$ $T(V)$ , а скорее $T (V ∗) {\ displaystyle T (V ^ {*})}$ $T(V^*)$ : (однородная) линейная функция на V является элементом $V ∗, {\ displaystyle V ^ {*},}$ $V ^ {*},$ например, координаты $x 1,…, xn {\ displaystyle x ^ {1}, \ dots, x ^ {n}}$ $x^1,\dots,x^n$ в векторном пространстве - это ковекторы, поскольку они принимают вектор и выдают скаляр (заданную координату вектора).

Факторы

Из-за общности тензорной алгебры многие другие интересующие алгебры могут быть построены, начав с тензорной алгебры и затем наложив определенные отношения на генераторы, т. Е. Построив определенные фактор-алгебры алгебры T (V). Примерами этого являются внешняя алгебра, симметрическая алгебра, алгебры Клиффорда, алгебра Вейля и универсальные обертывающие алгебры.

Коалгебра

Тензорная алгебра имеет две разные структуры коалгебры. Один из них совместим с тензорным произведением и, таким образом, может быть расширен до биалгебры и может быть дополнительно расширен с помощью антипода к структуре алгебры Хопфа. Другая структура, хотя и более простая, не может быть распространена на биалгебру. Первая структура развивается непосредственно ниже; вторая структура дана в разделе cofree коалгебры ниже.

Представленное ниже развитие может быть одинаково хорошо применено к внешней алгебре, используя символ клина $∧ {\ displaystyle \ wedge}$ $\ wedge$ вместо символ тензора $⊗ {\ displaystyle \ otimes}$ $\otimes$ ; знак также необходимо отслеживать при перестановке элементов внешней алгебры. Это соответствие длится также до определения биалгебры и до определения алгебры Хопфа. То есть внешней алгебре также может быть задана структура алгебры Хопфа.

Точно так же симметрической алгебре можно точно так же придать структуру алгебры Хопфа, заменив везде тензорное произведение $⊗ {\ displaystyle \ otimes}$ $\otimes$ симметризованным тензорным произведением $⊗ S ym {\ displaystyle \ otimes _ {\ mathrm {Sym}}}$ ${\ displaystyle \ otimes _ {\ mathrm {Sym}}}$ , то есть тем произведением, где $v ⊗ S ymw = w ⊗ S ymv. {\ displaystyle v \ otimes _ {\ mathrm {Sym}} w = w \ otimes _ {\ mathrm {Sym}} v.}$ $v\otimes _{\mathrm {Sym} }w=w\otimes _{\mathrm {Sym} }v.$

В любом случае это возможно, потому что чередующийся продукт $∧ {\ displaystyle \ wedge}$ $\ wedge$ и симметричное произведение $⊗ S ym {\ displaystyle \ otimes _ {\ mathrm {Sym}}}$ ${\ displaystyle \ otimes _ {\ mathrm {Sym}}}$ подчиняются необходимым условиям согласованности для определения биалгебра и алгебра Хопфа; это можно явно проверить следующим образом. Всякий раз, когда у кого-то есть продукт, удовлетворяющий этим условиям консистенции, конструкция идет тщательно; поскольку такое произведение привело к фактор-пространству, фактор-пространство наследует структуру алгебры Хопфа.

На языке теории категорий говорится, что существует функтор T из категории K-векторных пространств в категорию K-ассоциированных алгебр. Но есть также функтор Λ, переводящий векторные пространства в категорию внешних алгебр, и функтор Sym, переводящий векторные пространства в симметрические алгебры. Существует естественная карта от T до каждого из них. Проверка того, что факторизация сохраняет структуру алгебры Хопфа, аналогична проверке того, что отображения действительно естественны.

Копродукт

Коалгебра получается путем определения копродукта или диагонального оператора

Δ: TV → TV ⊠ TV {\ displaystyle \ Delta: TV \ to TV \ boxtimes TV}

\Delta :TV\to TV\boxtimes TV

Здесь $TV {\ displaystyle TV}$ ${\ displaystyle TV}$ используется как сокращение от $T (V) {\ displaystyle T (V)}$ $T(V)$ во избежание взрыва скобок. Символ $⊠ {\ displaystyle \ boxtimes}$ $\ boxtimes$ используется для обозначения «внешнего» тензорного произведения, необходимого для определения коалгебры. Он используется, чтобы отличить его от «внутреннего» тензорного произведения $⊗ {\ displaystyle \ otimes}$ $\otimes$ , которое уже «занято» и используется для обозначения умножения в тензорной алгебре (см. раздел Умножение, ниже, для дальнейших разъяснений по этому вопросу). Чтобы избежать путаницы между этими двумя символами, в большинстве текстов $⊗ {\ displaystyle \ otimes}$ $\otimes$ будет заменяться простой точкой или даже полностью исключаться, понимая, что это подразумевается из контекста.. Затем это позволяет использовать символ $⊗ {\ displaystyle \ otimes}$ $\otimes$ вместо символа $⊠ {\ displaystyle \ boxtimes}$ $\ boxtimes$ . Ниже этого не делается, и два символа используются независимо и явно, чтобы показать правильное расположение каждого из них. Результат будет немного более подробным, но его будет легче понять.

Определение оператора $Δ {\ displaystyle \ Delta}$ $\Delta$ проще всего построить поэтапно, сначала определив его для элементов $v ∈ V ⊂ TV { \ displaystyle v \ in V \ subset TV}$ $v\in V\subset TV$ , а затем гомоморфно расширив его на всю алгебру. Тогда подходящим выбором для совместного произведения является

Δ: v ↦ v ⊠ 1 + 1 ⊠ v {\ displaystyle \ Delta: v \ mapsto v \ boxtimes 1 + 1 \ boxtimes v}

\Delta :v\mapsto v\boxtimes 1+1\boxtimes v

Δ: 1 ↦ 1 ⊠ 1 {\ Displaystyle \ Delta: 1 \ mapsto 1 \ boxtimes 1}

{\ displaystyle \ Delta: 1 \ mapsto 1 \ boxtimes 1}

где $1 ∈ K = T 0 V ⊂ TV {\ displaystyle 1 \ in K = T ^ {0} V \ subset TV}$ ${\ displaystyle 1 \ in K = T ^ {0} V \ subset TV}$ - единица измерения поля $K {\ displaystyle K}$ $K$ . По линейности очевидно, что

Δ (k) = k (1 ⊠ 1) = k ⊠ 1 = 1 ⊠ k {\ displaystyle \ Delta (k) = k (1 \ boxtimes 1) = k \ boxtimes 1 = 1 \ boxtimes k}

{\ displaystyle \ Delta (k) = k (1 \ boxtimes 1) = k \ boxtimes 1 = 1 \ boxtimes k}

для всех $k ∈ K. {\ displaystyle k \ in K.}$ $k\in K.$ Несложно убедиться, что это определение удовлетворяет аксиомам коалгебры: то есть

(id TV ⊠ Δ) ∘ Δ = (Δ ⊠ id TV) ∘ Δ {\ displaystyle (\ mathrm {id} _ {TV} \ boxtimes \ Delta) \ circ \ Delta = (\ Delta \ boxtimes \ mathrm {id} _ {TV}) \ circ \ Delta}

(\mathrm {id} _{TV}\boxtimes \Delta)\circ \Delta =(\Delta \boxtimes \mathrm {id} _{TV})\circ \Delta

где $id TV: x ↦ x {\ displaystyle \ mathrm {id} _ {TV}: x \ mapsto x}$ ${\ displaystyle \ mathrm {id} _ {TV}: x \ mapsto x}$ - карта идентичности на $TV {\ displaystyle TV}$ ${\ displaystyle TV}$ . Действительно, получаем

((id TV ⊠ Δ) ∘ Δ) (v) = v ⊠ 1 ⊠ 1 + 1 ⊠ v ⊠ 1 + 1 ⊠ 1 ⊠ v {\ displaystyle ((\ mathrm {id} _ { TV} \ boxtimes \ Delta) \ circ \ Delta) (v) = v \ boxtimes 1 \ boxtimes 1 + 1 \ boxtimes v \ boxtimes 1 + 1 \ boxtimes 1 \ boxtimes v}

{\ displaystyle ((\ mathrm {id } _ {TV} \ boxtimes \ Delta) \ circ \ Delta) (v) = v \ boxtimes 1 \ boxtimes 1 + 1 \ boxtimes v \ boxtimes 1 + 1 \ boxtimes 1 \ boxtimes v}

и аналогично для другой стороны. На этом этапе можно было бы использовать лемму и сказать, что $Δ {\ displaystyle \ Delta}$ $\Delta$ тривиально, линейно, распространяется на все $TV {\ displaystyle TV}$ ${\ displaystyle TV}$ , поскольку $TV {\ displaystyle TV}$ ${\ displaystyle TV}$ - это свободный объект, а $V {\ displaystyle V}$ $V$ - генератор свободной алгебры, а $Δ {\ displaystyle \ Delta}$ $\Delta$ является гомоморфизмом. Тем не менее, полезно предоставлять явные выражения. Итак, для $v ⊗ w ∈ T 2 V {\ displaystyle v \ otimes w \ in T ^ {2} V}$ ${\ displaystyle v \ otimes w \ in T ^ {2} V}$ , каждый имеет (по определению) гомоморфизм

Δ: v ⊗ вес ↦ Δ (v) ⊗ Δ (w) {\ displaystyle \ Delta: v \ otimes w \ mapsto \ Delta (v) \ otimes \ Delta (w)}

\Delta :v\otimes w\mapsto \Delta (v)\otimes \Delta (w)

Расширяясь, мы получаем

Δ (v ⊗ вес) знак равно (v ⊠ 1 + 1 ⊠ v) ⊗ (w ⊠ 1 + 1 ⊠ w) = (v ⊗ w) ⊠ 1 + v ⊠ w + w ⊠ v + 1 ⊠ (v ⊗ w) {\ displaystyle {\ begin {align} \ Delta (v \ otimes w) = (v \ boxtimes 1 + 1 \ boxtimes v) \ otimes (w \ boxtimes 1 + 1 \ boxtimes w) \\ = (v \ otimes w) \ boxtimes 1 + v \ boxtimes w + w \ boxtimes v + 1 \ boxtimes (v \ otimes w) \ end {align}}}

{\ displaystyle {\ begin {align} \ Delta (v \ otimes w) = (v \ boxtimes 1 + 1 \ boxtimes v) \ otimes (w \ boxtimes 1 +1 \ boxtimes w) \\ = (v \ otimes w) \ boxtimes 1 + v \ boxtimes w + w \ boxtimes v + 1 \ boxtimes (v \ otimes w) \ end {align}}}

В приведенном выше расширении нет необходимости писать $1 ⊗ v {\ displaystyle 1 \ otimes v}$ ${\ displaystyle 1 \ otimes v }$ , поскольку это просто старое скалярное умножение в алгебре; то есть, очевидно, что $1 ⊗ v = 1 ⋅ v = v. {\ displaystyle 1 \ otimes v = 1 \ cdot v = v.}$ $1\otimes v=1\cdot v=v.$

Приведенное выше расширение сохраняет градуировку алгебры. То есть

Δ: T 2 V → ⨁ k = 0 2 T k V ⊠ T (2 - k) V {\ displaystyle \ Delta: T ^ {2} V \ to \ bigoplus _ {k = 0} ^ {2} T ^ {k} V \ boxtimes T ^ {(2-k)} V}

{\ displaystyle \ Delta: T ^ {2} V \ to \ bigoplus _ {k = 0} ^ {2} T ^ {k} V \ boxtimes T ^ {(2-k)} V}

Продолжая таким образом, можно получить явное выражение для совместного произведения, действующего на однородный элемент порядка m:

Δ (v 1 ⊗ ⋯ ⊗ vm) = Δ (v 1) ⊗ ⋯ ⊗ Δ (vm) = ∑ p = 0 m (v 0 ⊗ ⋯ ⊗ vp) ω (vp + 1 ⊗ ⋯ ⊗ vm) = ∑ p = 0 m ∑ σ ∈ S h (p, m - p + 1) (v σ (0) ⊗ ⋯ ⊗ v σ (p)) ⊠ (v σ (p + 1) ⊗ ⋯ ⊗ v σ (m)) {\ displaystyle {\ begin {align} \ Delta (v_ {1} \ otimes \ cdots \ otimes v_ {m}) = \ Delta (v_ {1}) \ otimes \ cdots \ otimes \ Delta (v_ {m }) \\ = \ sum _ {p = 0} ^ {m} \ left (v_ {0} \ otimes \ cdots \ otimes v_ {p} \ right) \; \ omega \; \ left (v_ {p +1} \ otimes \ cdots \ otimes v_ {m} \ right) \\ = \ sum _ {p = 0} ^ {m} \; \ sum _ {\ sigma \ in \ mathrm {Sh} (p, m-p + 1)} \; \ left (v _ {\ sigma (0)} \ otimes \ dots \ otimes v _ {\ sigma (p)} \ right) \ boxtimes \ left (v _ {\ sigma (p + 1)} \ otimes \ dots \ otimes v _ {\ sigma (m)} \ right) \ end {align}}}

{\ displaystyle {\ begin {align} \ Дельта (v_ {1} \ otimes \ cdots \ otimes v_ {m}) = \ Delta (v_ {1}) \ otimes \ cdots \ otimes \ Delta (v_ {m}) \\ = \ sum _ {p = 0} ^ {m} \ left (v_ {0} \ otimes \ cdots \ otimes v_ {p} \ right) \; \ omega \; \ left (v_ {p + 1} \ otimes \ cdots \ otimes v_ { m} \ right) \\ = \ sum _ {p = 0} ^ {m} \; \ sum _ {\ sigma \ in \ mathrm {Sh} (p, m-p + 1)} \; \ left (v _ {\ sigma (0)} \ otimes \ dots \ otimes v _ {\ sigma (p)} \ right) \ boxtimes \ left (v _ {\ sigma (p + 1)} \ otimes \ dots \ otimes v _ {\ сигма (м)} \ справа) \ конец {выровнено}}}

, где $ω {\ displaystyle \ omega}$ Символ $\ omega$ , который должен выглядеть как ш, обозначает произведение в случайном порядке. Это выражается во втором суммировании, которое проводится по всем (p, m-p + 1) -shuffles. Вышеупомянутое написано с помощью нотации, чтобы отслеживать элемент поля 1: уловка состоит в том, чтобы написать $v 0 = 1 {\ displaystyle v_ {0} = 1}$ ${\ displaystyle v_ {0} = 1}$ , и это перетасовывается в различные места во время раскрытия суммы путем перемешивания. Перемешивание непосредственно следует из первой аксиомы коалгебры: относительный порядок элементов $vk {\ displaystyle v_ {k}}$ $v_ {k}$ сохраняется в перемешивании: перемешивание просто разделяется упорядоченную последовательность на две упорядоченные последовательности, одну слева и одну справа. Любая заданная перетасовка подчиняется

σ (0) < ⋯ < σ ( p) and σ ( p + 1) < ⋯ < σ ( m) {\displaystyle \sigma (0)<\cdots <\sigma (p)\quad {\t_dv{ and }}\quad \sigma (p+1)<\cdots <\sigma (m)}

{\ displayst yle \ sigma (0) <\ cdots <\ sigma (p) \ quad {\ t_dv {and}} \ quad \ sigma (p + 1) <\ cdots <\ sigma (m)}

Как и раньше, алгебраическая градуировка сохраняется:

Δ: T m V → ⨁ k = 0 m T k V ⊠ T (m - k) V { \ displaystyle \ Delta: T ^ {m} V \ to \ bigoplus _ {k = 0} ^ {m} T ^ {k} V \ boxtimes T ^ {(mk)} V}

\Delta :T^{m}V\to \bigoplus _{k=0}^{m}T^{k}V\boxtimes T^{(m-k)}V

Counit

Счетчик $ϵ: TV → K {\ displaystyle \ epsilon: TV \ to K}$ $\epsilon :TV\to K$ задается проекцией компонента поля из алгебры. Это можно записать как $ϵ: v ↦ 0 {\ displaystyle \ epsilon: v \ mapsto 0}$ $\epsilon :v\mapsto 0$ для $v ∈ V {\ displaystyle v \ in V}$ $v \ in V$ и $ϵ: К ↦ К {\ displaystyle \ epsilon: k \ mapsto k}$ ${\ displaystyle \ epsilon: k \ mapsto k}$ для $k ∈ K = T 0 V {\ displaystyle k \ in K = T ^ {0 } V}$ ${\ displaystyle k \ in K = T ^ {0} V}$ . По гомоморфизму под тензорным произведением $⊗ {\ displaystyle \ otimes}$ $\otimes$ это распространяется на

ϵ: x ↦ 0 {\ displaystyle \ epsilon: x \ mapsto 0}

{\ displaystyle \ epsilon: х \ mapsto 0}

для всех $x ∈ T 1 V ⊕ T 2 V ⊕ ⋯ {\ displaystyle x \ in T ^ {1} V \ oplus T ^ {2} V \ oplus \ cdots}$ ${\ displaystyle x \ in T ^ {1} V \ oplus T ^ {2} V \ oplus \ cdots}$ Это прямой вперед, чтобы убедиться, что эта коучта удовлетворяет необходимой аксиоме для коалгебры:

(id ⊠ ϵ) ∘ Δ = id = (ϵ ⊠ id) ∘ Δ. {\ displaystyle (\ mathrm {id} \ boxtimes \ epsilon) \ circ \ Delta = \ mathrm {id} = (\ epsilon \ boxtimes \ mathrm {id}) \ circ \ Delta.}

(\ mathrm {id} \boxtimes \epsilon)\circ \Delta =\mathrm {id} =(\epsilon \boxtimes \mathrm {id})\circ \Delta.

Работая с этим явно, имеет

((id ⊠ ϵ) ∘ Δ) (x) = (id ⊠ ϵ) (1 ⊠ x + x ⊠ 1) = 1 ⊠ ϵ (x) + x ⊠ ϵ (1) = 0 + x ⊠ 1 ≅ Икс {\ Displaystyle {\ begin {выровнен} ((\ mathrm {id} \ boxtimes \ epsilon) \ circ \ Delta) (x) = (\ mathrm {id} \ boxtimes \ epsilon) (1 \ boxtimes x + x \ boxtimes 1) \\ = 1 \ boxtimes \ epsilon (x) + x \ boxtimes \ epsilon (1) \\ = 0 + x \ boxtimes 1 \\ \ cong x \ end {выровнено}}}

{\ displaystyle {\ begin {align} (( \ mathrm {id} \ boxtimes \ epsilon) \ circ \ Delta) (x) = (\ mathrm {id} \ boxtimes \ epsilon) (1 \ boxtimes x + x \ boxtimes 1) \\ = 1 \ boxtimes \ эпсилон (х) + х \ boxtimes \ epsilon (1) \\ = 0 + x \ boxtimes 1 \\ \ cong x \ end {выравнивается}}}

где на последнем шаге использовался изоморфизм $TV ⊠ K ≅ TV {\ displaystyle TV \ boxtimes K \ cong TV}$ $TV\boxtimes K\cong TV$ , что соответствует определяющей аксиоме графства.

Биалгебра

A биалгебра определяет как умножение, так и коумножение, и требует, чтобы они были совместимы.

Умножение

Умножение задается оператором

∇: TV ⊠ TV → TV {\ displaystyle \ nabla: TV \ boxtimes TV \ to TV}

{\ displaystyle \ nabla: TV \ boxtimes TV \ to TV}

который в этом случай, уже был задан как «внутреннее» тензорное произведение. То есть

∇: x ⊠ y ↦ x ⊗ y {\ displaystyle \ nabla: x \ boxtimes y \ mapsto x \ otimes y}

{\ displaystyle \ nabla: x \ boxtimes y \ mapsto x \ otimes y}

То есть $∇ (x ⊠ y) = x ⊗ у. {\ displaystyle \ nabla (x \ boxtimes y) = x \ otimes y.}$ ${\ displaystyle \ nabla (x \ boxtimes y) = x \ otimes y.}$ Из приведенного выше должно быть ясно, почему символ $⊠ {\ displaystyle \ boxtimes}$ $\ boxtimes$ нуждается в для использования: $⊗ {\ displaystyle \ otimes}$ $\otimes$ на самом деле было тем же самым, что и $∇ {\ displaystyle \ nabla}$ $\ nabla$ ; а небрежность в обозначениях привела бы к полному хаосу. Чтобы усилить это: тензорное произведение $⊗ {\ displaystyle \ otimes}$ $\otimes$ тензорной алгебры соответствует умножению $∇ {\ displaystyle \ nabla}$ $\ nabla$ , используемому в определение алгебры, тогда как тензорное произведение $⊠ {\ displaystyle \ boxtimes}$ $\ boxtimes$ - это то, что требуется в определении коумножения в коалгебре. Эти два тензорных произведения - не одно и то же!

Единица

Единица для алгебры

η: K → TV {\ displaystyle \ eta: K \ to TV}

\eta :K\to TV

- это просто вложение, так что

η: k ↦ k {\ displaystyle \ eta: k \ mapsto k}

{\ displaystyle \ eta: k \ mapsto k}

То, что единица измерения совместима с тензорным произведением $⊗ {\ displaystyle \ otimes}$ $\otimes$ , «тривиально»: it является лишь частью стандартного определения тензорного произведения векторных пространств. То есть $k ⊗ x = k x {\ displaystyle k \ otimes x = kx}$ $k\otimes x=kx$ для элемента поля k и любого $x ∈ T V. {\ displaystyle x \ in TV.}$ $x\in TV.$ Точнее говоря, аксиомы для ассоциативной алгебры требуют двух гомоморфизмов (или коммутирующих диаграмм):

∇ ∘ (η ⊠ id TV) = η ⊗ id TV = η ⋅ id TV {\ displaystyle \ nabla \ circ (\ eta \ boxtimes \ mathrm {id} _ {TV}) = \ eta \ otimes \ mathrm {id} _ {TV} = \ eta \ cdot \ mathrm {id} _ {TV}}

{\ displaystyle \ nabla \ circ (\ eta \ boxtimes \ mathrm {id} _ {TV}) = \ eta \ otimes \ mathrm {id} _ {TV} = \ eta \ cdot \ mathrm {id} _ {TV}}

на $K ⊠ TV {\ displaystyle K \ boxtimes TV}$ ${\ displaystyle K \ boxtimes TV}$ , и симметрично, на $TV ⊠ K {\ displaystyle TV \ boxtimes K}$ $TV\boxtimes K$ , что

∇ ∘ (id TV ⊠ η) = id TV ⊗ η = id TV ⋅ η {\ displaystyle \ nabla \ circ (\ mathrm {id} _ { TV} \ boxtimes \ eta) = \ mathrm {id} _ {TV} \ otimes \ eta = \ mathrm {id} _ {TV} \ cdot \ eta}

{\ displaystyle \ nabla \ circ (\ mathrm {id} _ {TV} \ boxtimes \ eta) = \ mathrm {id} _ {TV} \ otimes \ eta = \ mathrm {id} _ {TV} \ cdot \ eta}

где правая часть этих уравнений должна быть понимается как скалярное произведение.

Совместимость

Единица и число, а также умножение и коумножение должны удовлетворять условиям совместимости. Несложно видеть, что

η ∘ ϵ = i d K. {\ displaystyle \ eta \ circ \ epsilon = \ mathrm {id} _ {K}.}

\eta \circ \epsilon =\mathrm {id} _{K}.

Аналогично, единица измерения совместима с коумножением:

Δ ∘ η = η ⊠ η ≅ η {\ displaystyle \ Delta \ circ \ eta = \ eta \ boxtimes \ eta \ cong \ eta}

{\ displaystyle \ Delta \ circ \ eta = \ eta \ boxtimes \ eta \ cong \ eta }

Вышеупомянутое требует использования изоморфизма $K ⊠ K ≅ K {\ displaystyle K \ boxtimes K \ cong K}$ ${\ displaystyle K \ boxtimes K \ cong K}$ чтобы работать; без этого теряется линейность. По компонентам

(Δ ∘ η) (k) = Δ (k) = k (1 ⊠ 1) ≅ k {\ displaystyle (\ Delta \ circ \ eta) (k) = \ Delta (k) = k (1 \ boxtimes 1) \ cong k}

(\Delta \circ \eta)(k)=\Delta (k)=k(1\boxtimes 1)\cong k

с правой частью, использующей изоморфизм.

Умножение и счетчик совместимы:

(ϵ ∘ ∇) (x ⊠ y) = ϵ (x ⊗ y) = 0 {\ displaystyle (\ epsilon \ circ \ nabla) (x \ boxtimes y) = \ epsilon (x \ otimes y) = 0}

(\epsilon \circ \nabla)(x\boxtimes y)=\epsilon (x\otimes y)=0

всякий раз, когда x или y не являются элементами $K {\ displaystyle K}$ $K$ , и в противном случае используется скалярное умножение на поле: $k 1 ⊗ k 2 = k 1 k 2. {\ displaystyle k_ {1} \ otimes k_ {2} = k_ {1} k_ {2}.}$ $k_{1}\otimes k_{2}=k_{1}k_{2}.$ Сложнее всего проверить совместимость умножения и коумножения:

Δ ∘ ∇ = (∇ ⊠ ∇) ∘ (id ⊠ τ ⊠ id) ∘ (Δ ⊠ Δ) {\ displaystyle \ Delta \ circ \ nabla = (\ nabla \ boxtimes \ nabla) \ circ (\ mathrm {id} \ boxtimes \ tau \ boxtimes \ mathrm {id}) \ circ (\ Delta \ boxtimes \ Delta)}

{\ displaystyle \ Delta \ circ \ набла = (\ набла \ боксы \ набла) \ сирк (\ математика {id} \ бокс таймс \ тау \ бокс таймс \ математика {ид}) \ сирк (\ Дельта \ бокс таймс \ Дельта)}

где $τ (x ⊠ y) = y ⊠ x {\ displaystyle \ tau (x \ boxtimes y) = y \ boxtimes x}$ ${\ displaystyle \ tau (x \ boxtimes y) = y \ boxtimes x}$ меняет местами элементы. Условие совместимости необходимо проверить только на $V ⊂ T V {\ displaystyle V \ subset TV}$ ${\ displaystyle V \ subset TV}$ ; полная совместимость следует как гомоморфное расширение на все $T V. {\ displaystyle TV.}$ $TV.$ Проверка подробна, но прямолинейна; здесь он не приводится, за исключением окончательного результата:

(Δ ∘ ∇) (v ⊠ w) = Δ (v ⊗ w) {\ displaystyle (\ Delta \ circ \ nabla) (v \ boxtimes w) = \ Delta (v \ otimes w)}

{\ displaystyle (\ Delta \ circ \ nabla) (v \ boxtimes w) = \ Delta (v \ otimes w)}

Для $v, w ∈ V, {\ displaystyle v, w \ in V,}$ $v,w\in V,$ явное выражение для этого было дано в разделе коалгебры, над.

Алгебра Хопфа

Алгебра Хопфа добавляет антипод к аксиомам биалгебры. Антипод $S {\ displaystyle S}$ $S$ на $k ∈ K = T 0 V {\ displaystyle k \ in K = T ^ {0} V}$ ${\ displaystyle k \ in K = T ^ {0} V}$ является задается как

S (k) = k {\ displaystyle S (k) = k}

{\ displaystyle S (k) = k}

Иногда это называют «антиидентификацией». Антипод на $v ∈ V = T 1 V {\ displaystyle v \ in V = T ^ {1} V}$ ${\ displaystyle v \ in V = T ^ { 1} V}$ задается выражением

S (v) = - v {\ displaystyle S (v) = - v}

{\ displaystyle S (v) = -v}

и на $v ⊗ w ∈ T 2 V {\ displaystyle v \ otimes w \ in T ^ {2} V}$ ${\ displaystyle v \ otimes w \ in T ^ {2} V}$ по

S (v ⊗ вес) знак равно S (вес) ⊗ S (v) = вес ⊗ v {\ Displaystyle S (v \ otimes w) = S (w) \ otimes S (v) = w \ otimes v}

S(v\otimes w)=S(w)\otimes S(v)=w\otimes v

Это продолжается гомоморфно до

S (v 1 ⊗ ⋯ ⊗ vm) = S (vm) ⊗ ⋯ ⊗ S (v 1) = (- 1) mvm ⊗ ⋯ ⊗ v 1 {\ displaystyle {\ begin {align} S ( v_ {1} \ otimes \ cdots \ otimes v_ {m}) = S (v_ {m}) \ otimes \ cdots \ otimes S (v_ {1}) \\ = (- 1) ^ {m} v_ {m} \ otimes \ cdots \ otimes v_ {1} \ end {align}}}

{\ Displaystyle {\ begin {выровнено} S (v_ {1} \ otimes \ cdots \ otimes v_ {m}) = S (v_ {m}) \ otimes \ cdots \ otimes S (v_ {1}) \\ = (- 1) ^ {m} v_ {m} \ otimes \ cdots \ otimes v_ {1} \ end {align}}}

Совместимость

Совместимость антипода с умножением и коумножением требует, чтобы

∇ ∘ (S ⊠ id) ∘ Δ знак равно η ∘ ϵ знак равно ∇ ∘ (id ⊠ S) ∘ Δ {\ displaystyle \ nabla \ circ (S \ boxtimes \ mathrm {id}) \ circ \ Delta = \ eta \ circ \ epsilon = \ nabla \ circ ( \ mathrm {id} \ boxtimes S) \ circ \ Delta}

\nabla \circ (S\boxtimes \mathrm {id})\circ \Delta =\eta \circ \epsilon =\nabla \circ (\mat hrm {id} \boxtimes S)\circ \Delta

Это легко проверить покомпонентно на $k ∈ K {\ displaystyle k \ in K }$ $k\in K$ :

(∇ ∘ (S ⊠ id) ∘ Δ) (k) = (∇ ∘ (S ⊠ id)) (1 ⊠ k) = ∇ (1 ⊠ k) = 1 ⊗ k = k {\ displaystyle { \ begin {align} (\ nabla \ circ (S \ boxtimes \ mathrm {id}) \ circ \ Delta) (k) = (\ nabla \ circ (S \ boxtimes \ mathrm {id})) (1 \ boxtimes k) \\ = \ nabla (1 \ boxtimes k) \\ = 1 \ otimes k \\ = k \ end {align}}}

{\begin{aligned}(\nabla \circ (S\boxtimes \mathrm {id})\circ \Delta)(k)=(\nabla \circ (S\boxtimes \mathrm {id}))(1\boxtimes k)\\=\nabla (1\boxtimes k)\\=1\otimes k\\=k\end{aligned}}

Аналогично, на $v ∈ V {\ displaystyle v \ in V}$ $v \ in V$ :

(∇ ∘ (S ⊠ id) ∘ Δ) (v) = (∇ ∘ (S ⊠ id)) (v ⊠ 1 + 1 ⊠ v) = ∇ (- v ⊠ 1 + 1 ⊠ v) знак равно - v ⊗ 1 + 1 ⊗ v = - v + v знак равно 0 {\ Displaystyle {\ begin {выровнено} (\ nabla \ circ (S \ boxtimes \ mathrm {id}) \ circ \ Delta) (v) = (\ nabla \ circ (S \ boxtimes \ mathrm {id})) (v \ boxtimes 1 + 1 \ boxtimes v) \\ = \ nabla (-v \ boxtimes 1 + 1 \ boxtimes v) \\ = -v \ otimes 1 + 1 \ otimes v \\ = - v + v \\ = 0 \ end {align}}}

{\ displaystyle {\ begin {align} (\ набла \ circ (S \ boxtimes \ mathrm {id}) \ circ \ Delta) (v) = (\ nabla \ circ (S \ boxtimes \ mathrm {id})) (v \ boxtimes 1 + 1 \ boxtimes v) \\ = \ nabla (-v \ boxtimes 1 + 1 \ boxtimes v) \\ = - v \ otimes 1 + 1 \ otimes v \\ = - v + v \\ = 0 \ end {выровнено} }}

Напомним, что

(η ∘ ϵ) (k) = η ( k) знак равно К {\ Displaystyle (\ eta \ circ \ epsilon) (k) = \ eta (k) = k}

{\ displaystyle (\ eta \ circ \ epsilon) (k) = \ eta (k) = k}

и что

(η ∘ ϵ) (x) = η (0) = 0 {\ displaystyle (\ eta \ circ \ epsilon) (x) = \ eta (0) = 0}

(\eta \circ \epsilon)(x)=\eta (0)=0

для любого $x ∈ TV {\ displaystyle x \ in TV}$ $x\in TV$ , которого нет в $К. {\ displaystyle K.}$ $K.$

Можно поступить аналогичным образом, путем гомоморфизма, убедившись, что антипод вставляет соответствующие знаки отмены в тасование, начиная с условия совместимости на $T 2 V {\ displaystyle T ^ {2} V}$ ${\ Displaystyle T ^ {2} V}$ и далее по индукции.

Кополная коалгебра Cofree

На тензорной алгебре можно определить другое копроизведение, более простое, чем приведенное выше. Он задается выражением

Δ (v 1 ⊗ ⋯ ⊗ vk): = ∑ j = 0 k (v 0 ⊗ ⋯ ⊗ vj) ⊠ (vj + 1 ⊗ ⋯ ⊗ vk + 1) {\ displaystyle \ Delta (v_ {1} \ otimes \ dots \ otimes v_ {k}): = \ sum _ {j = 0} ^ {k} (v_ {0} \ otimes \ dots \ otimes v_ {j}) \ boxtimes (v_ {j +1} \ otimes \ dots \ otimes v_ {k + 1})}

{\ displaystyle \ Delta (v_ {1} \ otimes \ dots \ otimes v_ {k}): = \ sum _ {j = 0} ^ {k} (v_ {0} \ otimes \ dots \ otimes v_ {j}) \ boxtimes (v_ {j + 1} \ otimes \ dots \ otimes v_ {k + 1})}

Здесь, как и раньше, используется нотационный трюк $v 0 = vk + 1 = 1 ∈ K {\ displaystyle v_ {0} = v_ {k + 1} = 1 \ in K}$ $v_{0}=v_ {k+1}=1\in K$ (напомним, что $v ⊗ 1 = v {\ displaystyle v \ otimes 1 = v}$ ${\ displaystyle v \ otimes 1 = v}$ банально).

Этот копродукт дает начало коалгебре. Он описывает коалгебру, которая двойственная к структуре алгебры на T (V), где V обозначает двойственное векторное пространство линейных отображений V → F . Точно так же, как тензорная алгебра является свободной алгеброй, соответствующая коалгебра называется кополной соввободной. С обычным продуктом это не биалгебра. Его можно превратить в биалгебру с помощью произведения $vi ⋅ vj = (i, j) vi + j {\ displaystyle v_ {i} \ cdot v_ {j} = (i, j) v_ {i + j} }$ $v_{i}\cdot v_{j}=(i,j)v_{i+j}$ где (i, j) обозначает биномиальный коэффициент для $(i + ji) {\ displaystyle {\ tbinom {i + j} {i}}}$ ${\tbinom {i+j}{i}}$ . Эта биалгебра известна как алгебра Хопфа с разделенными степенями.

. Разницу между этой и другой коалгеброй легче всего увидеть в $T 2 V {\ displaystyle T ^ {2} V}$ ${\ Displaystyle T ^ {2} V}$ срок. Здесь

Δ (v ⊗ w) = 1 ⊠ (v ⊗ w) + v ⊠ w + (v ⊗ w) ⊠ 1 {\ displaystyle \ Delta (v \ otimes w) = 1 \ boxtimes ( v \ otimes w) + v \ boxtimes w + (v \ otimes w) \ boxtimes 1}

{\ displaystyle \ Delta (v \ otimes w) = 1 \ boxtimes (v \ otimes w) + v \ boxtimes w + (v \ otimes w) \ boxtimes 1}

для $v, w ∈ V {\ displaystyle v, w \ in V}$ $v,w\in V$ , что явно отсутствует перетасованный термин по сравнению с предыдущим.

См. Также

Литература

Бурбаки, Николас (1989). Алгебра I. Главы 1-3. Элементы математики. Спрингер-Верлаг. ISBN 3-540-64243-9. (см. Главу 3 §5)

Серж Лэнг (2002), алгебра, выпускные тексты по математике, 211 (3-е изд.), Springer Verlag, ISBN 978-0-387-95385-4