Обобщенное распределение экстремальных значений

редактировать

Обозначение	$GEV (μ, σ, ξ) {\ displaystyle {\ textrm {GEV}} (\ mu, \, \ sigma, \, \ xi)}$ $\ textrm {GEV} (\ mu, \, \ sigma, \, \ xi)$
Параметры	μ ∈ R— местоположение,. σ>0 - масштаб,. ξ ∈ R— shape.
Поддержка	x ∈ [μ - σ / ξ, + ∞) при ξ>0,. x ∈ (−∞, + ∞) при ξ = 0,. x ∈ (−∞, μ - σ / ξ], когда ξ < 0.
PDF	$1 σ t (x) ξ + 1 e - t (x), {\ displaystyle {\ frac {1} {\ sigma} } \, t (x) ^ {\ xi +1} e ^ {- t (x)},}$ $\ frac {1} { \ sigma} \, t (x) ^ {\ xi + 1} e ^ {- t (x)},$ где $t (x) = {(1 + ξ (x - μ σ)) - 1 / ξ, если ξ ≠ 0 e - (x - μ) / σ, если ξ = 0 {\ displaystyle t (x) = {\ begin {cases} {\ big (} 1+ \ xi ({\ tfrac {x- \ mu} {\ sigma}}) {\ big)} ^ {- 1 / \ xi} {\ textrm {if}} \ \ xi \ neq 0 \\ e ^ {- (x- \ mu) / \ sigma} {\ textrm {if}} \ \ xi = 0 \ end {cases}}}$ ${\ displaystyle t (x) = {\ begin {cases} {\ big (} 1+ \ xi ({\ tfrac {x- \ mu} {\ sigma}}) {\ big)} ^ {- 1 / \ xi} { \ textrm {if}} \ \ xi \ neq 0 \\ e ^ {- (x- \ mu) / \ sigma} {\ textrm {if}} \ \ xi = 0 \ end {cases}}}$
CDF	$e - t (x), {\ displaystyle e ^ {- t (x)}, \,}$ $e ^ {- t (x)}, \,$ для x ∈ support
Среднее	${μ + σ (g 1 - 1) / ξ, если ξ ≠ 0, ξ < 1, μ + σ γ if ξ = 0, ∞ if ξ ≥ 1, {\displaystyle {\begin{cases}\mu +\sigma (g_{1}-1)/\xi {\text{if}}\ \xi \neq 0,\xi <1,\\\mu +\sigma \,\gamma {\text{if}}\ \xi =0,\\\infty {\text{if}}\ \xi \geq 1,\end{cases}}}$ ${\ displaystyle {\ begin {case} \ mu + \ sigma (g_ {1} -1) / \ xi {\ text {if}} \ xi \ neq 0, \ xi <1, \\\ mu + \ sigma \, \ гамма {\ текст {если}} \ \ xi = 0, \\\ infty {\ text {if}} \ \ xi \ geq 1, \ end {cases}}}$ где g k= Γ (1 - kξ),. и $γ {\ displaystyle \ gamma}$ $\ gamma$ - константа Эйлера t.
Медиана	${μ + σ (ln ⁡ 2) - ξ - 1 ξ, если ξ ≠ 0, μ - σ ln ⁡ ln ⁡ 2, если ξ = 0. {\ displaystyle {\ begin {cases} \ mu + \ sigma {\ frac {(\ ln 2) ^ {- \ xi} -1} {\ xi}} {\ text {if}} \ \ xi \ neq 0, \\\ mu - \ sigma \ ln \ ln 2 {\ text {if}} \ \ xi = 0. \ end {ases}}}$ $\ begin {cases} \ mu + \ sigma \ frac {(\ ln2) ^ {- \ xi} - 1} {\ xi} \ text {if} \ xi \ neq0, \\ \ mu - \ sigma \ ln \ ln2 \ text {if} \ \ xi = 0. \ End {cases}$
Режим	${μ + σ (1 + ξ) - ξ - 1 ξ, если ξ ≠ 0, μ, если ξ = 0. {\ displaystyle {\ begin {cases} \ mu + \ sigma {\ frac {(1+ \ xi) ^ {- \ xi} -1} {\ xi}} {\ text {if }} \ \ xi \ neq 0, \\\ mu {\ text {if}} \ \ xi = 0. \ end {cases}}}$ $\ begin {case} \ mu + \ sigma \ frac {(1+ \ xi) ^ {- \ xi} -1} {\ xi} \ text {if} \ xi \ neq0, \\ \ mu \ text {if} \ \ xi = 0. \ end {case}$
Дисперсия	${σ 2 (g 2 - g 1 2) / ξ 2, если ξ ≠ 0, ξ < 1 2, σ 2 π 2 6 if ξ = 0, ∞ if ξ ≥ 1 2, {\displaystyle {\begin{cases}\sigma ^{2}\,(g_{2}-g_{1}^{2})/\xi ^{2}{\text{if}}\ \xi \neq 0,\xi <{\frac {1}{2}},\\\sigma ^{2}\,{\frac {\pi ^{2}}{6}}{\text{if}}\ \xi =0,\\\infty {\text{if}}\ \xi \geq {\frac {1}{2}},\end{cases}}}$ $\ begin {cases} \ sigma ^ 2 \, (g_2-g_1 ^ 2) / \ xi ^ 2 \ text {if} \ \ xi \ neq0, \ xi <\ frac12, \\ \ sigma ^ 2 \, \ frac {\ pi ^ 2} {6} \ text {if} \ \ xi = 0, \\ \ infty \ text {if} \ \ xi \ geq \ frac12, \ end {cases}$ .
Асимметрия	${sgn ⁡ (ξ) g 3 - 3 g 2 g 1 + 2 g 1 3 (g 2 - g 1 2) 3/2, если ξ ≠ 0, ξ < 1 3, 12 6 ζ ( 3) π 3 if ξ = 0. {\displaystyle {\begin{cases}\operatorname {sgn}(\xi){\frac {g_{3}-3g_{2}g_{1}+2g_{1}^{3}}{(g_{2}-g_{1}^{2})^{3/2}}}{\text{if}}\ \xi \neq 0,\xi <{\frac {1}{3}},\\{\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}{\text{if}}\ \xi =0.\end{cases}}}$ ${\ displaystyle {\ begin {case} \ operatorname {sgn} (\ xi) {\ f рац {g_ {3} -3g_ {2} g_ {1} + 2g_ {1} ^ {3}} {(g_ {2} -g_ {1} ^ {2}) ^ {3/2}}} {\ text {if}} \ \ xi \ neq 0, \ xi <{\ frac {1} {3}}, \\ {\ frac {12 {\ sqrt {6}} \, \ zeta (3)} {\ pi ^ {3}}} {\ text {if}} \ \ xi = 0. \ end {cases}}}$ . где $sign ⁡ (x) {\ displaystyle \ operatorname {sgn} (x)}$ $\ operatorname {sgn} (x)$ - знаковая функция . и $ζ (x) {\ displaystyle \ zeta (x)}$ $\ zeta (x)$ - это дзета-функция Римана
Пример. эксцесс	${g 4 - 4 g 3 g 1 - 3 g 2 2 + 12 g 2 g 1 2 - 6 g 1 4 (g 2 - g 1 2) 2 если ξ ≠ 0, ξ < 1 4, 12 5 if ξ = 0. {\displaystyle {\begin{cases}{\frac {g_{4}-4g_{3}g_{1}-3g_{2}^{2}+12g_{2}g_{1}^{2}-6g_{1}^{4}}{(g_{2}-g_{1}^{2})^{2}}}{\text{if}}\ \xi \neq 0,\xi <{\frac {1}{4}},\\{\frac {12}{5}}{\text{if}}\ \xi =0.\end{cases}}}$ ${\ displaystyle {\ начать{ case} {\ frac {g_ {4} -4g_ {3} g_ {1} -3g_ {2} ^ {2} + 12g_ {2} g_ {1} ^ {2} -6g_ {1} ^ {4} } {(g_ {2} -g_ {1} ^ {2}) ^ {2}}} {\ text {if}} \ \ xi \ neq 0, \ xi <{\ frac {1} {4} }, \\ {\ frac {12} {5}} {\ text {if}} \ \ xi = 0. \ end {cases}}}$
Энтропия	$журнал ⁡ (σ) + γ ξ + γ + 1 {\ displaystyle \ log (\ sigma) \, + \, \ gamma \ xi \, + \, \ gamma \, + \, 1}$ ${\ displaystyle \ log (\ sigma) \, + \, \ gamma \ xi \, + \, \ гамма \, + \, 1}$
MGF
CF

В теории вероятностей и статистике, обобщенное экстремальное значение (GEV ) распределение является семейством непрерывных распределений вероятностей, разработанных в рамках теории экстремальных значений для объединения также известных семейств Gumbel, Fréchet и Weibull как распределения экстремальных значений I, II и III типов. Согласно теореме об экстремальных значениях распределение GEV является единственно возможным предельным распределением правильно нормализованных максимумов последовательности независимых и одинаково распределенных случайных величин. Обратите внимание, что должно существовать предельное распределение, которое требует условий регулярности в хвосте распределения. Несмотря на это, распределение GEV часто используется в качестве приближения для моделирования максимумов длинных (конечных) последовательностей случайных величин.

В некоторых областях применения обобщенное распределение экстремальных значений известно как распределение Фишера – Типпетта, названное в честь Рональда Фишера и Л. Х. К. Типпет, который распознал три различные формы, описанные ниже. Однако использование этого имени иногда ограничивается особым случаем распределения Gumbel. Происхождение общей функциональной формы для всех трех дистрибутивов восходит, по крайней мере, к Дженкинсону, А.Ф. (1955), хотя якобы это могло быть также дано Мизесом, Р. (1936).

Содержание

1 Спецификация
2 Сводная статистика
3 Ссылка на семейства Fréchet, Weibull и Gumbel
- 3.1 Изменение минимумов, а не максимумов
- 3.2 Альтернативное соглашение для распределения Вейбулла
- 3.3 Диапазоны распределений
- 3.4 Распределение переменных журнала
4 Ссылка на модели логита (логистическая регрессия)
5 Свойства
6 Приложения
- 6.1 Пример для нормально распределенных переменных
7 Связанные распределения
- 7.1 Доказательства
8 См. также
9 Ссылки
10 Дополнительная литература

Спецификация

Использование стандартизованной переменной $s = (x - μ) / σ, {\ displaystyle s = (x- \ mu) / \ sigma \,,}$ ${\ displaystyle s = (x- \ mu) / \ sigma \,,}$ где $μ, {\ displaystyle \ mu \,,}$ ${\ displaystyle \ mu \,,}$ параметр местоположения, может быть любым действительным числом, а $σ>0 {\ displaystyle \ sigma>0}$ $\sigma>0$ - параметр масштаба; тогда кумулятивная функция распределения GEV-распределения равна

F (s; ξ) = {exp ⁡ (- exp ⁡ (- s)) для ξ = 0 exp ⁡ (- (1 + ξ s) - 1 / ξ) для ξ ≠ 0 и ξ s>- 1 0 для ξ>0 и ξ s ≤ - 1 1 для ξ < 0 and ξ s ≤ − 1, {\displaystyle F(s;\xi)={\begin{cases}\exp {\Bigl (}-\exp(-s){\Bigr)}~~{\text{ for }}~~\xi =0\\{}\\\exp {\Bigl (}-(1+\xi s)^{-1/\xi }{\Bigr)}~~{\text{ for }}~~\xi \neq 0~~{\text{ and }}~~\xi \,s>-1 \\ {} \\ 0 ~~ {\ text {for}} ~~ \ xi>0 ~~ {\ text {and}} ~~ \ xi \, s \ leq -1 \\ {} \\ 1 ~~ {\ text {for}} ~~ \ xi <0~~{\text{ and }}~~\xi \,s\leq -1~,\end{cases}}}

F(s;\xi)={\begin{cases}\exp {\Bigl (}-\exp(-s){\Bigr)}~~{\text{ for }}~~\xi =0\\{}\\\exp {\Bigl (}-(1+\xi s)^{-1/\xi }{\Bigr)}~~{\text{ for }}~~\xi \neq 0~~{\text{ and }}~~\xi \,s>-1 \\ { } \\ 0 ~~ {\ text {for}} ~~ \ xi>0 ~~ {\ text {and}} ~~ \ xi \, s \ leq -1 \\ {} \\ 1 ~~ {\ text {for}} ~~ \ xi <0~~{\text{ and }}~~\xi \,s\leq -1~,\end{cases}}

где $ξ, {\ displaystyle \ xi \,,}$ ${\ displaystyle \ xi \,,}$ параметр формы, может быть любым действительным числом. Таким образом, для $ξ>0 {\ displaystyle \ xi>0}$ $\xi>0$ , выражение действительно для $s>- 1 / ξ, {\ displaystyle s>-1 / \ xi \,,}$ $s>-1 / \ xi \,,$ в то время как для $ξ < 0 {\displaystyle \xi <0}$ ${\ displaystyle \ xi <0}$ это действительно для $s < − 1 / ξ. {\displaystyle s<-1/\xi \,.}$ ${\ displaystyle s <-1 / \ xi \,.}$ . В первом случае $- 1 / ξ {\ displaystyle -1 / \ xi}$ ${\ displaystyle -1 / \ xi}$ - отрицательная нижняя конечная точка, где $F {\ displaystyle F}$ $F$ равно 0; во втором случае $- 1 / ξ {\ displaystyle -1 / \ xi}$ ${\ displaystyle -1 / \ xi}$ - положительная верхняя конечная точка, где $F {\ displaystyle F}$ $F$ равно 1. Для $ξ = 0 {\ displaystyle \ xi = 0}$ $\ xi = 0$ второе выражение формально не определено и заменяется первым выражением, которое является результатом взятия предела во-вторых, как $ξ → 0 {\ displaystyle \ xi \ to 0}$ ${\ displaystyle \ xi \ to 0}$ , и в этом случае $s {\ displaystyle s}$ $s$ может быть любым действительным числом.

В частном случае среднего $x = μ, {\ displaystyle x = \ mu \,,}$ ${\ displaystyle x = \ mu \,,}$ поэтому $s = 0 {\ displaystyle s = 0 }$ $s Знак равно 0$ и $F (s; ξ) = ехр ⁡ (- 1) {\ displaystyle F (s; \ xi) = \ exp (-1)}$ ${\ displaystyle F (s; \ xi) = \ ехр (-1)}$ ≈ $0,368 {\ displaystyle 0,368 }$ ${\ displaystyle 0.368}$ для любых значений $ξ {\ displaystyle \ xi}$ $\ xi$ и $σ {\ displaystyle \ sigma}$ $\ sigma$ , которые могут иметь.

Функция плотности вероятности стандартизованного распределения:

f (s; ξ) = {exp ⁡ (- s) exp ⁡ (- exp ⁡ (- s)) для ξ = 0 (1 + ξ s) - (1 + 1 / ξ) exp ⁡ (- (1 + ξ s) - 1 / ξ) для ξ ≠ 0 и ξ s>- 1 0 в противном случае, {\ displaystyle f (s; \ xi) = {\ begin {case} \ exp (-s) \ exp {\ Bigl (} - \ exp (-s) {\ Bigr)} ~~ {\ text {for}} ~~ \ xi = 0 \\ { } \\ {\ Bigl (} 1+ \ xi s {\ Bigr)} ^ {- (1 + 1 / \ xi)} \ exp {\ Bigl (} - (1+ \ xi s) ^ {- 1 / \ xi} {\ Bigr)} ~~ {\ text {for}} ~~ \ xi \ neq 0 ~~ {\ text {and}} ~~ \ xi \, s>-1 \\ {} \\ 0 ~~ {\ text {в противном случае}} \ end {cases}}}

f(s;\xi)={\begin{cases}\exp(-s)\exp {\Bigl (}-\exp(-s){\Bigr)}~~{\text{ for }}~~\xi =0\\{}\\{\Bigl (}1+\xi s{\Bigr)}^{-(1+1/\xi)}\exp {\Bigl (}-(1+\xi s)^{-1/\xi }{\Bigr)}~~{\text{ for }}~~\xi \neq 0~~{\text{ and }}~~\xi \,s>-1 \\ {} \\ 0 ~~ {\ text {иначе,}} \ end {ases}}

снова действительно для $s>- 1 / ξ {\ displaystyle s>-1 / \ xi}$ $s>-1 / \ xi$ в случае $ξ>0, {\ displaystyl e \ xi>0 \,,}$ $\xi>0 \,,$ и для $s < − 1 / ξ {\displaystyle s<-1/\xi }$ ${\ displaystyle s <-1 / \ xi}$ в случае $ξ < 0. {\displaystyle \xi <0\,.}$ ${\ displaystyle \ xi <0\,.}$ плотность равна нулю за пределами соответствующего диапазона. В случае $ξ = 0 {\ displaystyle \ xi = 0}$ $\ xi = 0$ плотность положительна на всей действительной прямой.

Поскольку кумулятивная функция распределения обратима, функция квантиля для распределения GEV имеет явное выражение, а именно

Q (p; μ, σ, ξ) = {μ - σ log ⁡ (- log ⁡ (p)) для ξ = 0 и p ∈ (0, 1) μ + σ ξ ((- log ⁡ (p)) - ξ - 1) для ξ>0 и p ∈ [0, 1) или ξ < 0 and p ∈ ( 0, 1 ], {\displaystyle Q(p;\mu,\sigma,\xi)={\begin{cases}\mu -\sigma \log {\Bigl (}-\log \left(p\right)\,{\Bigr)}~{\text{ for }}~\xi =0~{\text{ and }}~p\in \left(0,1\right)\\{}\\\mu +\displaystyle {{\,\sigma \,} \over {\,\xi \,}}\left({\Bigl (}-\log(p)\,{\Bigr)}^{-\xi }-1\right)~{\text{ for }}~\xi>0 ~ {\ text {and}} ~ p \ in \ left [0,1 \ right) \\ {} ~~ {\ text {or}} ~ \, \ xi <0~{\text{ and }}~p\in (0,1]\;,\end{cases}}}

Q(p;\mu,\sigma,\xi)={\begin{cases}\mu -\sigma \log {\Bigl (}-\log \left(p\right)\,{\Bigr)}~{\text{ for }}~\xi =0~{\text{ and }}~p\in \left(0,1\right)\\{}\\\mu +\displaystyle {{\,\sigma \,} \over {\,\xi \,}}\left({\Bigl (}-\log(p)\,{\Bigr)}^{-\xi }-1\right)~{\text{ for }}~\xi>0 ~ {\ text {and}} ~ p \ in \ left [0,1 \ right) \\ {} ~~ {\ text {or}} ~ \, \ xi <0~{\text{ and }}~p\in (0,1]\;,\end{cases}}

и, следовательно, функция плотности квантиля $( q ≡ d ⁡ Q d ⁡ п) {\ displaystyle \ left (q \ Equiv {\ frac {\; \ operatorname {d} Q \;} {\ operatorname {d} p}} \ right)}$ ${\ displaystyle \ left (q \ Equiv {\ frac {\; \ operatorname {d} Q \;} {\ operatorname {d} p}} \ right)}$ равно

q (p; σ, ξ) = σ (- журнал ⁡ (p)) ξ + 1 p для p ∈ (0, 1), {\ displaystyle q (p; \ sigma, \ xi) = {\ frac {\ sigma} {\; {\ Bigl (} - \ log \ left (p \ right) \, {\ Bigr)} ^ {\ xi +1} \, p \,}} \ quad { \ text {for}} ~~ p \ in \ left (0,1 \ right) \ ;,}

{\ displaystyle q (p; \ sigma, \ xi) = {\ frac {\ sigma} {\; {\ Bigl (} - \ log \ left (p \ right) \, {\ Bigr)} ^ {\ xi +1} \, p \,} } \ quad {\ text {for}} ~~ p \ in \ left (0,1 \ right) \ ;,}

действительно для $σ>0 {\ displaystyle ~ \ sigma>0 ~}$ $~\sigma>0 ~$ и для любого реального $ξ. {\ displaystyle ~ \ xi \ ;.}$ ${\ displaystyle ~ \ xi \ ;.}$

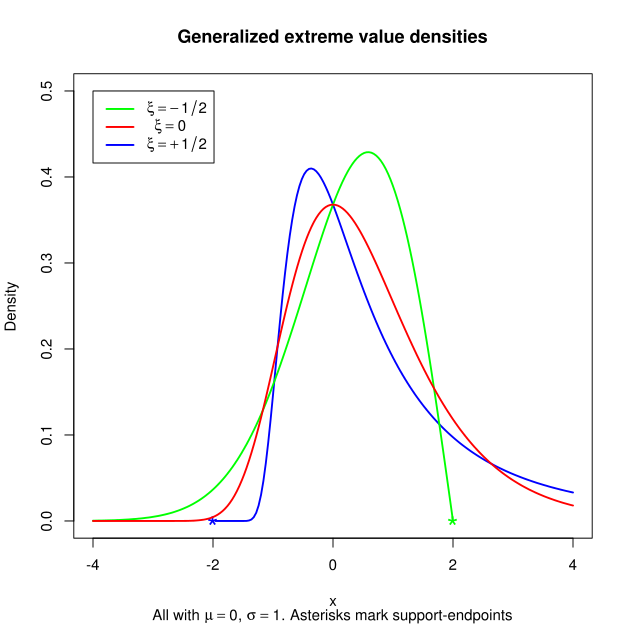
Сводная статистика

Вот некоторые простые статистические данные распределения:

E ⁡ (X) = μ + (g 1 - 1) σ ξ {\ displaystyle \ operatorname {E} (X) = \ mu + \ left (g_ {1} -1 \ right) {\ frac {\ sigma} {\ xi}}}

{\ displaystyle \ operatorname {E} (X) = \ mu + \ left (g_ {1} -1 \ right) {\ frac {\ sigma} {\ xi}}}

для

ξ < 1 {\displaystyle \xi <1}

{\ displaystyle \ xi <1}

Var ⁡ (Икс) знак равно (г 2 - г 1 2) σ 2 ξ 2, {\ displaystyle \ operatorname {Var} (X) = \ left (g_ {2} -g_ {1} ^ {2} \ right) {\ frac {\ sigma ^ {2}} {\ xi ^ {2}}},}

{\ displaystyle \ operatorname {Var} (X) = \ left (g_ {2} -g_ {1} ^ {2} \ right) {\ frac {\ sigma ^ {2}} {\ xi ^ {2}}},}

Режим ⁡ (X) = μ + σ ξ [(1 + ξ) - ξ - 1]. {\ displaystyle \ operatorname {Mode} (X) = \ mu + {\ frac {\ sigma} {\ xi}} [(1+ \ xi) ^ {- \ xi} -1].}

\ operatorname {Mode} (X) = \ mu + \ frac {\ sigma} { \ xi} [(1+ \ xi) ^ {- \ xi} -1].

асимметрия означает ξ>0

асимметрия ⁡ (X) = g 3 - 3 g 2 g 1 + 2 g 1 3 (g 2 - g 1 2) 3/2 {\ displaystyle \ operatorname { асимметрия} (X) = {\ frac {g_ {3} -3g_ {2} g_ {1} + 2g_ {1} ^ {3}} {(g_ {2} -g_ {1} ^ {2}) ^ {3/2}}}}

{\ displaystyle \ operatorname {skewness} (X) = {\ frac {g_ {3} -3g_ {2} g_ {1} + 2g_ {1} ^ {3}} {(g_ {2} -g_ {1} ^ {2}) ^ {3/2}}}}

Для ξ <0, the sign of the numerator is reversed.

превышение эксцесса составляет:

эксцесс эксцесс ⁡ (X) = г 4 - 4 г 3 г 1 + 6 г 2 г 1 2 - 3 г 1 4 (г 2 - г 1 2) 2 - 3. {\ Displaystyle \ OperatorName {эксцесс \ избыток} (X) = {\ frac {g_ {4} -4g_ {3} g_ { 1} + 6g_ {2} g_ {1} ^ {2} -3g_ {1} ^ {4}} {(g_ {2} -g_ {1} ^ {2}) ^ {2}}} - 3. }

{\ displaystyle \ operatorname {эксцесс \ превышение} (X) = {\ frac {g_ {4} -4g_ {3} g_ {1} + 6g_ {2} g_ {1} ^ {2} -3g_ {1} ^ {4}} {(g_ {2} -g_ {1} ^ {2}) ^ {2}}} - 3.}

где $gk = Γ (1 - k ξ) {\ displaystyle g_ {k} = \ Gamma (1-k \ xi)}$ $g_k = \ Gamma (1-k \ xi)$ , k = 1,2,3, 4 и $Γ (t) {\ displaystyle \ Gamma (t)}$ $\Gamma(t)$ - это гамма-функция.

Ссылка на семейства Фреше, Вейбулла и Гамбеля

Параметр формы $ξ {\ displaystyle \ xi}$ $\ xi$ управляет поведением хвоста распределения. Подсемейства, определенные в $ξ = 0 {\ displaystyle \ xi = 0}$ $\ xi = 0$ , $ξ>0 {\ displaystyle \ xi>0}$ $\xi>0$ и $ξ < 0 {\displaystyle \xi <0}$ $\ xi <0$ соответствуют, соответственно, семействам Гамбель, Фреше и Вейбулла кумулятивные функции распределения показаны ниже.

Гамбель или распределение экстремальных значений типа I ( $ξ = 0 {\ displaystyle \ xi = 0}$ $\ xi = 0$ )

F (x; μ, σ, 0) = e - е - (x - μ) / σ для x ∈ R. {\ displaystyle F (x; \ mu, \ sigma, 0) = e ^ {- e ^ {- (x- \ mu) / \ sigma}} \; \; \; {\ text {for}} \; \; x \ in \ mathbb {R}.}

F (x; \ mu, \ sigma, 0) = e ^ {- e ^ {- (x- \ mu) / \ sigma}} \; \; \; \ text {for} \; \; x \ in \ mathbb R.

Фреше или распределение экстремальных значений типа II, если $ξ = α - 1>0 {\ displaystyle \ xi = \ alpha ^ {- 1}>0}$ $\xi=\alpha^{-1}>0$ и $y = 1 + ξ (x - μ) / σ {\ displaystyle y = 1 + \ xi (x- \ mu) / \ sigma }$ $y = 1 + \ xi (x- \ mu) / \ sigma$

F (x; μ, σ, ξ) знак равно {е - Y - α Y>0 0 Y ≤ 0. {\ Displaystyle F (x; \ mu, \ sigma, \ xi) = {\ begin {cases} e ^ {- y ^ {- \ alpha}} y>0 \\ 0 y \ leq 0. \ end {ases}}}

$F(x;\mu,\sigma,\xi)=\begin{cases} e^{-y^{-\alpha}} y>0 \\ 0 y \ leq 0. \ end {ases}$

Перевернутое Weibull или тип III extreme распределение значений, если $ξ = - α - 1 < 0 {\displaystyle \xi =-\alpha ^{-1}<0}$ $\ xi = - \ alpha ^ {- 1} <0$ и $y = - (1 + ξ (x - μ) / σ) {\ displaystyle y = - \ left (1+ \ xi (x - \ mu) / \ sigma \ right)}$ ${\ displaystyle y = - \ left (1+ \ xi (x- \ mu) / \ sigma \ right)}$

F (x; μ, σ, ξ) = {e - (- y) α y < 0 1 y ≥ 0 {\displaystyle F(x;\mu,\sigma,\xi)={\begin{cases}e^{-(-y)^{\alpha }}y<0\\1y\geq 0\end{cases}}}

F (x; \ mu, \ sigma, \ xi) = \ begin {cases} e ^ {- (- y) ^ {\ alpha}} y <0 \\ 1 y \ geq 0 \ end {case}

В следующих пунктах упоминаются свойства этих распределений.

Модификация для минимумов, а не для максимумов

Теория здесь относится к максимумам данных, и обсуждаемое распределение является распределением экстремальных значений для максимумов. Обобщенное распределение экстремальных значений для минимумов данных может быть получено, например, заменой (-x) вместо x в функции распределения и вычитанием из единицы: это дает отдельное семейство распределений.

Альтернативное соглашение для распределения Вейбулла

Обычное распределение Вейбулла возникает в приложениях надежности и получается из распределения здесь с использованием переменной $t = μ - x {\ displaystyle t = \ mu -x}$ $t = \ mu - x$ , что дает строго положительную поддержку - в отличие от использования здесь в теории экстремальных значений. Это происходит потому, что обычное распределение Вейбулла используется в случаях, когда речь идет о минимумах данных, а не о максимумах данных. Распределение здесь имеет дополнительный параметр по сравнению с обычной формой распределения Вейбулла и, кроме того, обратное, так что распределение имеет верхнюю границу, а не нижнюю границу. Важно отметить, что в приложениях GEV верхняя граница неизвестна и поэтому должна быть оценена, в то время как при применении обычного распределения Вейбулла в приложениях надежности нижняя граница обычно равна нулю.

Диапазоны распределений

Обратите внимание на различия в диапазонах, представляющих интерес для трех распределений экстремальных значений: Gumbel не ограничен, Fréchet имеет нижний предел, тогда как перевернутый Weibull имеет верхний предел. Точнее, Теория экстремальных значений (Теория одномерных) описывает, какой из трех является ограничивающим законом в соответствии с исходным законом X и, в частности, в зависимости от его хвоста.

Распределение переменных журнала

Тип I можно связать с типами II и III следующим образом: если кумулятивная функция распределения некоторой случайной величины $X {\ displaystyle X}$ $X$ относится к типу II и с положительными числами в качестве опоры, т. Е. $F (x; 0, σ, α) {\ displaystyle F (x; 0, \ sigma, \ alpha)}$ $F (х; 0, \ sigma, \ alpha)$ , то кумулятивная функция распределения $ln ⁡ X {\ displaystyle \ ln X}$ $\ пер Икс$ имеет тип I, а именно $F (x; ln ⁡ σ, 1 / α, 0) {\ Displaystyle F (x; \ ln \ sigma, 1 / \ alpha, 0)}$ $F (x ; \ ln \ sigma, 1 / \ alpha, 0)$ . Аналогично, если кумулятивная функция распределения $X {\ displaystyle X}$ $X$ относится к типу III и с отрицательными числами в качестве поддержки, то есть $F (x; 0, σ, - α) {\ displaystyle F (x; 0, \ sigma, - \ alpha)}$ $F (x; 0, \ sigma, - \ alpha)$ , то кумулятивная функция распределения $ln ⁡ (- X) {\ displaystyle \ ln (-X)}$ $\ ln (-X)$ относится к типу I, а именно: $F (x; - ln ⁡ σ, 1 / α, 0) {\ displaystyle F (x; - \ ln \ sigma, 1 / \ alpha, 0) }$ $F (x; - \ ln \ sigma, 1 / \ alpha, 0)$ .

Ссылка на логит-модели (логистическая регрессия)

Полиномиальные логит-модели и некоторые другие типы логистической регрессии могут быть сформулированы как модели скрытых переменных с переменные ошибок распределены как распределения Гамбеля (обобщенные распределения экстремальных значений типа I). Эта формулировка распространена в теории моделей дискретного выбора, которые включают логит-модели, пробит-модели и различные их расширения, и происходит из того факта, что разница двух переменных, распределенных GEV типа I, следует логистическому распределению, из которых логит-функция является функцией квантиля. Таким образом, распределение GEV типа I играет в этих логит-моделях ту же роль, что и нормальное распределение в соответствующих пробит-моделях.

Свойства

кумулятивная функция распределения обобщенного распределения экстремальных значений решает уравнение постулата устойчивости. Обобщенное распределение экстремальных значений является частным случаем max-устойчивого распределения и представляет собой преобразование min-устойчивого распределения.

Приложения

Распределение GEV широко используется для обработки «хвостовых рисков» в самых разных областях, от страхования до финансов. В последнем случае это рассматривалось как средство оценки различных финансовых рисков с помощью таких показателей, как Стоимость под риском.

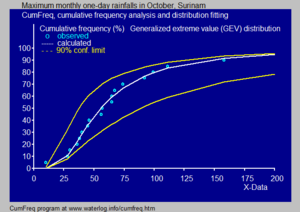
Соответствующее распределение вероятности GEV для месячных максимальных однодневных осадков в октябре, Суринам

Однако, было обнаружено, что результирующие параметры формы лежат в диапазоне, ведущем к неопределенным средним и дисперсиям, что подчеркивает тот факт, что надежный анализ данных часто невозможен.

В гидрологии распределение GEV применяется к экстремальным явлениям например, максимальное годовое количество осадков за один день и сток рек. Синяя картинка, сделанная с помощью CumFreq, иллюстрирует пример подгонки распределения GEV к ранжированным годовым максимальным однодневным осадкам, показывая также 90% доверительный пояс на основе бинома . распределение. Данные об осадках представлены позициями как часть кумулятивного частотного анализа.

Пример для нормально распределенных переменных

Пусть $(X i) i ∈ [n ] {\ displaystyle (X_ {i}) _ {i \ in [n]}}$ ${\ displaystyle (X_ {i}) _ {i \ in [n]}}$ быть идентификатором. нормально распределенные случайные величины со средним 0 и дисперсией 1. Теорема Фишера – Типпета – Гнеденко говорит нам, что $max i ∈ [n] X i ∼ GEV (μ n, σ N, 0) {\ Displaystyle \ max _ {я \ in [n]} X_ {i} \ sim GEV (\ mu _ {n}, \ sigma _ {n}, 0)}$ ${\ displaystyle \ max _ {i \ in [n]} X_ {i} \ sim GEV (\ mu _ {n}, \ sigma _ {n}, 0)}$ , где

$μ n = Φ - 1 (1 - 1 n) σ n = Φ - 1 (1 - 1 n ⋅ e - 1) - Φ - 1 (1 - 1 n) {\ displaystyle {\ begin { выровнено} \ mu _ {n} = \ Phi ^ {- 1} \ left (1 - {\ frac {1} {n}} \ right) \\\ sigma _ {n} = \ Phi ^ {- 1} \ left (1 - {\ frac {1} {n}} \ cdot \ mathrm {e} ^ {- 1} \ right) - \ Phi ^ {- 1} \ left (1 - {\ frac {1 } {n}} \ right) \ end {align}}}$ ${\ displaystyle {\ begin {align} \ mu _ {n} = \ Phi ^ {- 1} \ left (1 - {\ frac {1} {n}} \ right) \ \\ sigma _ {n} = \ Phi ^ {- 1} \ left (1 - {\ frac {1} {n}} \ cdot \ mathrm {e} ^ {- 1} \ right) - \ Phi ^ {-1} \ left (1 - {\ frac {1} {n}} \ right) \ end {align}}}$ .

Это позволяет нам оценить, например, среднее значение $max i ∈ [n] X i {\ displaystyle \ max _ {i \ in [n]} X_ {i}}$ ${\ displaystyle \ max _ {i \ in [n]} X_ {i}}$ от среднего значения распределения GEV:

$E [max i ∈ [n] X i] ≈ μ n + γ σ n = (1 - γ) Φ - 1 (1 - 1 / n) + γ Φ - 1 (1 - 1 / (en)) = журнал ⁡ (N 2 2 π журнал ⁡ (N 2 2 π)) ⋅ (1 + γ журнал ⁡ (n) + о (1 журнал ⁡ (n))) {\ Displaystyle {\ begin {выровненный} E \ left [\ max _ {i \ in [n]} X_ {i} \ right] \ приблизительно \ mu _ {n} + \ gamma \ sigma _ {n} \\ = (1- \ gamma) \ Phi ^ {- 1} (1-1 / n) + \ gamma \ Phi ^ {- 1} (1-1 / (en)) \\ = {\ sqrt {\ log \ left ({\ frac {n ^ {2} } {2 \ pi \ log \ left ({\ frac {n ^ {2}} {2 \ pi}} \ right)}} \ right)}} \ cdot \ left (1 + {\ frac {\ gamma} {\ log (n)}} + {\ mathcal {o}} \ left ({\ frac {1} {\ log (n)}} \ right) \ right) \ end {align}}}$ ${\ displaystyle {\ begin {align} E \ left [\ max _ {i \ in [n]} X_ {i} \ right] \ приблизительно \ mu _ {n} + \ gamma \ sigma _ {n} \\ = (1- \ gamma) \ Phi ^ {- 1} (1 -1 / n) + \ gamma \ Phi ^ {- 1} (1-1 / (en)) \\ = {\ sqrt {\ log \ le ft ({\ frac {n ^ {2}} {2 \ pi \ log \ left ({\ frac {n ^ {2}} {2 \ pi}} \ right)}} \ right)}} \ cdot \ влево (1 + {\ frac {\ gamma} {\ log (n)}} + {\ mathcal {o}} \ left ({\ frac {1} {\ log (n)}} \ right) \ right) \ end {выровнен}}}$

Связанные распределения

Если $Икс ∼ GEV (μ, σ, ξ) {\ Displaystyle X \ sim {\ textrm {GEV}} (\ mu, \, \ sigma, \, \ xi)}$ ${\ displaystyle X \ sim {\ textrm {GEV}} (\ mu, \, \ sigma, \, \ xi)}$ , затем $m X + b ∼ GEV (m μ + b, m σ, ξ) {\ displaystyle mX + b \ sim {\ textrm {GEV}} (m \ mu + b, \, m \ sigma \, \ xi)}$ ${\ displaystyle mX + b \ sim {\ textrm {GEV} } (м \ му + б, \, м \ сигма, \, \ xi)}$
Если $X ∼ Gumbel (μ, σ) {\ displaystyle X \ sim {\ textrm {Gumbel}} (\ mu, \, \ sigma)}$ $X \ sim \ textrm {Gumbel} (\ mu, \, \ sigma)$ (распределение Гамбеля ), тогда $X ∼ GEV (μ, σ, 0) {\ displaystyle X \ sim {\ textrm {GEV}} (\ mu, \, \ sigma, \, 0)}$ $Икс \ sim \ textrm {GEV} (\ mu, \, \ sigma, \, 0)$
Если $X ∼ Weibull (σ, μ) {\ displaystyle X \ sim {\ textrm {Weibull}} (\ sigma, \, \ mu)}$ $X \ sim \ textrm {Weibull} (\ sigma, \, \ mu)$ (Weibull распределение ), затем $μ (1 - σ log X σ) ∼ GEV (μ, σ, 0) {\ displaystyle \ mu \ left (1- \ sigma \ mathrm {log} {\ tfrac {X}) {\ sigma}} \ right) \ sim {\ textrm {GEV}} (\ mu, \, \ sigma, \, 0)}$ $\ mu \ left (1- \ sigma \ mathrm {log} {\ tfrac {X} {\ sigma}} \ right) \ sim \ textrm {GEV} ( \ му, \, \ сигма, \, 0)$
Если $X ∼ GEV (μ, σ, 0) {\ displaystyle X \ sim {\ textrm {GEV}} (\ mu, \, \ sigma, \, 0)}$ $Икс \ sim \ textrm {GEV} (\ mu, \, \ sigma, \, 0)$ , затем $σ exp ⁡ (- X - μ μ σ) ∼ Weibull (σ μ) {\ displaystyle \ sigma \ exp (- {\ tfrac {X- \ mu} {\ mu \ sigma}}) \ sim {\ textrm {Weibull}} (\ sigma, \, \ mu)}$ $\ sigma \ exp (- \ tfrac {X- \ mu} {\ mu \ sigma}) \ sim \ textrm {Weibull} (\ sigma, \, \ mu)$ (Распределение Вейбулла )
Если $X ∼ Exponential (1) {\ displaystyle X \ sim {\ textrm {Exponential}} (1) \,}$ $Икс \ sim \ textrm {Экспоненциальный} (1) \,$ (Экспоненциальное распределение ), то $μ - σ журнал ⁡ Икс ∼ GEV (μ, σ, 0) {\ displaystyle \ mu - \ sigma \ log {X} \ sim {\ textrm {GEV}} (\ mu, \, \ sigma, \, 0)}$ $\ mu - \ sigma \ log {X} \ sim \ textrm {GEV} (\ mu, \, \ sigma, \, 0)$
Если $X ∼ G umbel (α X, β) { \ Displaystyle X \ sim \ mathrm {Gumbel} (\ alpha _ {X}, \ beta)}$ ${\ displaystyle X \ sim \ mathrm {Gumbel} (\ alpha _ {X}, \ beta)}$ и $Y ∼ G umbel (α Y, β) {\ displaystyle Y \ sim \ mathrm {Gumbel} (\ alpha _ {Y}, \ beta)}$ ${\ displaystyle Y \ sim \ mathrm {Gumbel} (\ alpha _ {Y}, \ beta)}$ затем $X - Y ∼ L ogistic (α X - α Y, β) {\ displaystyle XY \ sim \ mathrm {Logistic } (\ alpha _ {X} - \ alpha _ {Y}, \ beta) \,}$ ${\ displaystyle XY \ sim \ mathrm {Logistic} (\ alpha _ {X} - \ alpha _ {Y}, \ beta) \,}$ (см. Logistic_distribution ).
Если $X {\ displaystyle X}$ $X$ и $Y ∼ G зонтик (α, β) {\ displaystyle Y \ sim \ mathrm {Gumbel} (\ alpha, \ beta)}$ ${\ displaystyle Y \ sim \ mathrm {Gumbel} (\ alpha, \ beta)}$ , затем $X + Y ≁ L ogistic (2 α, β) {\ displaystyle X + Y \ nsim \ mathrm {Logistic} (2 \ alpha, \ beta) \,}$ ${\ displaystyle X + Y \ nsim \ mathrm {Logistic} (2 \ alpha, \ beta) \,}$ (сумма не является логистическим распределением). Обратите внимание, что $E (X + Y) = 2 α + 2 β γ ≠ 2 α = E (L ogistic (2 α, β)) {\ displaystyle E (X + Y) = 2 \ alpha +2 \ beta \ gamma \ neq 2 \ alpha = E \ left (\ mathrm {Logistic} (2 \ alpha, \ beta) \ right)}$ ${\ displaystyle E (X + Y) = 2 \ альфа +2 \ бета \ гамма \ neq 2 \ альфа = E \ влево (\ mathrm {Logistic} (2 \ alpha, \ beta) \ right)}$ .

Доказательства

4. Пусть $X ∼ Weibull (σ, μ) {\ displaystyle X \ sim {\ textrm {Weibull}} (\ sigma, \, \ mu)}$ $X \ sim \ textrm {Weibull} (\ sigma, \, \ mu)$ , тогда кумулятивное распределение $г (Икс) знак равно μ (1 - σ журнал Икс σ) {\ Displaystyle г (х) = \ му \ влево (1- \ sigma \ mathrm {log} {\ гидроразрыва {X} {\ sigma}} \ справа) }$ ${\ отображает tyle g (x) = \ mu \ left (1- \ sigma \ mathrm {log} {\ frac {X} {\ sigma}} \ right)}$ - это:

P (μ (1 - σ log ⁡ X σ) < x) = P ( log ⁡ X σ < 1 − x / μ σ) Since logarithm is always increasing: = P ( X < σ exp ⁡ [ 1 − x / μ σ ]) = 1 − exp ⁡ ( − ( σ exp ⁡ [ 1 − x / μ σ ] ⋅ 1 σ) μ) = 1 − exp ⁡ ( − ( exp ⁡ [ 1 μ − x / μ σ ]) μ) = 1 − exp ⁡ ( − exp ⁡ [ μ − x σ ]) = 1 − exp ⁡ ( − exp ⁡ [ − s ]), s = x − μ σ {\displaystyle {\begin{aligned}P(\mu \left(1-\sigma \log {\frac {X}{\sigma }}\right)

{\ displaystyle {\ begin {выровнено} P (\ mu \ left (1- \ sigma \ log {\ frac {X} {\ sigma}) } \ right) <x) = P \ left (\ log {\ frac {X} {\ sigma}} <{\ frac {1-x / \ mu} {\ sigma}} \ right) \\ { \ text {Поскольку логарифм всегда увеличивается:}} \\ = P \ left (X <\ sigma \ exp \ left [{\ frac {1-x / \ mu} {\ sigma}} \ right] \ right) \\ = 1- \ exp \ left (- \ left ({\ cancel {\ sigma}} \ exp \ left [{\ frac {1-x / \ mu} {\ sigma}} \ right] \ cdot { \ cancel {\ frac {1} {\ sigma}}} \ right) ^ {\ mu} \ right) \\ = 1- \ exp \ left (- \ left (\ exp \ left [{\ frac {{ \ cancelto {\ mu} {1}} - x / {\ cancel {\ mu}}} {\ sigma}} \ right] \ right) ^ {\ cancel {\ mu}} \ right) \\ = 1- \ exp \ left (- \ exp \ left [{\ frac {\ mu -x} {\ sigma}} \ right]\right)\\=1-\exp \left(-\exp \left[-s\right]\right),\quad s={\frac {x-\mu }{\sigma }}\ end{aligned}}}

который представляет собой cdf для $∼ GEV (μ, σ, 0) {\ displaystyle \ sim { \ textrm {GEV}} (\ mu, \, \ sigma, \, 0)}$ ${\ displaystyle \ sim { \ textrm {GEV}} (\ му, \, \ sigma, \, 0)}$ .

5. Пусть $X ∼ Exponential (1) {\ displaystyle X \ sim {\ textrm {Exponential}} (1)}$ ${\ displaystyle X \ sim {\ textrm {Exponential}} (1)}$ , тогда кумулятивное распределение $g (X) = μ - σ log ⁡ X {\ displaystyle g (X) = \ mu - \ sigma \ log {X}}$ ${\ displaystyle g (X) = \ mu - \ sigma \ log {X}}$ - это:

P (μ - σ log ⁡ X < x) = P ( log ⁡ ( X) < μ − x σ) since the logarithm is always increasing: = P ( X < exp ⁡ ( μ − x σ)) = 1 − exp ⁡ [ − exp ⁡ ( μ − x σ) ] = 1 − exp ⁡ [ − exp ⁡ ( − s) ], s = x − μ σ {\displaystyle {\begin{aligned}P(\mu -\sigma \log {X}

{\ Displaystyle {\ begin {выровнено} P (\ mu - \ sigma \ log {X} <x) = P \ left (\ log (X) <{\ frac {\ mu -x} {\ sigma }} \ right) \\ {\ text {, поскольку логарифм всегда увеличивается:}} \\ = P \ left (X <\ exp \ left ({\ frac {\ mu -x} {\ sigma}} \ right) \ right) \\ = 1- \ exp \ left [- \ exp \ left ({\ frac {\ mu -x} {\ sigma}} \ right) \ right] \\ = 1- \ exp \ left [- \ exp \ left (-s \ right) \ right], \ quad s = {\ frac {x- \ mu} {\ sigma}} \ end {ali gned}}}

, который представляет собой совокупное распределение $GEV (μ, σ, 0) {\ displaystyle {\ textrm {GEV}} (\ mu, \ sigma, 0)}$ ${\ displaystyle {\ textrm {GEV}} (\ mu, \ sigma, 0)}$ .

См. также

Теория экстремальных значений (теория одномерных)
Теорема Фишера – Типпета – Гнеденко
Обобщенное распределение Парето
Немецкая проблема танков, противоположный вопрос о численности населения максимум заданная выборка максимум
Выбрать ands – Balkema – de Haan, теорема

Ссылки

Дополнительная литература

Embrechts, Paul; Клюппельберг, Клаудия ; Микош, Томас (1997). Моделирование экстремальных событий для страхования и финансов. Берлин: Springer Verlag. ISBN 9783540609315.
Лидбеттер, М.Р., Линдгрен, Г. и Рутцен, Х. (1983). Крайности и связанные свойства случайных последовательностей и процессов. Springer-Verlag. ISBN 0-387-90731-9. CS1 maint: несколько имен: список авторов (ссылка )
Resnick, SI (1987). Экстремальные значения, регулярные вариации и точечные процессы. Springer-Verlag. ISBN 0-387-96481-9.
Коулс, Стюарт (2001). Введение в статистическое моделирование экстремальных значений. Springer-Verlag. ISBN 1-85233-459-2.