Фиктивная переменная (статистика)

В статистике и эконометрике, особенно в регрессионном анализе, фиктивная переменная - это переменная, которая принимает только значение 0 или 1, чтобы указать отсутствие или присутствие некоторого категориального эффекта, который, как можно ожидать, изменит результат. Их можно рассматривать как числовые заменители качественных фактов в регрессионной модели, сортировку данных по взаимоисключающим категориям (например, курящие и некурящие

Фиктивная независимая переменная (также называемая фиктивной независимой переменной), которая для некоторых наблюдений имеет значение 0, приведет к тому, что коэффициент этой переменной не будет иметь никакого значения воздействуя на зависимую переменную, в то время как, когда фиктивный элемент принимает значение 1, его коэффициент действует, чтобы изменить точку пересечения . Например, предположим, что членство в группе является одной из качественных переменных, относящихся к регрессии. Если членству в группе произвольно присвоено значение 1, тогда все остальные получат значение 0. Тогда перехват будет постоянным членом для нечленов, но будет постоянным членом плюс коэффициент фиктивной принадлежности членства в случае группы

Фиктивные переменные часто используются в анализе временных рядов с переключением режимов, сезонным анализом и приложениями качественных данных.

• 1 Включение фиктивной независимой
• 2 Модели ANOVA
  • 2.1 Модель ANOVA с одной качественной переменной
  • 2.2 Модель ANOVA с двумя качественными переменными
• 3 Модели ANCOVA
• 4 Взаимодействие между фиктивные переменные
• 5 фиктивные зависимые переменные
  • 5.1 Что произойдет, если зависимая переменная является фиктивной?
  • 5.2 Модели зависимых фиктивных переменных
    • 5.2.1 Линейная вероятностная модель
    • 5.2.2 Альтернативы LPM
    • 5.2.3 Модель Logit
    • 5.2.4 Модель Probit
• 6 См. Также
• 7 Ссылки
• 8 Дополнительная литература
• 9 Внешние ссылки

Рисунок 1 : График, показывающий заработную плату = α 0 + δ 0 женщина + α 1 образование + U, δ 0< 0.

Фиктивные переменные включены таким же образом, как и количественные переменные включены (как объясняющие переменные) в регрессионные модели. Например, если мы рассмотрим регрессионную модель типа Минсера определения заработной платы, в которой заработная плата зависит от пола (качественно) и лет образования (количественно):

$ln\; \; заработная\; плата\; =\; \alpha \; 0\; +\; \delta \; 0\; женщин\; +\; \alpha \; 1\; образование\; +\; u\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; text\; \{wage\}\}\; =\; \backslash \; alpha\; \_\; \{0\}\; +\; \backslash \; delta\; \_\; \{0\}\; \{\backslash \; text\; \{female\}\}\; +\; \backslash \; alpha\; \_\; \{1\}\; \{\backslash \; текст\; \{образование\}\}\; +\; u\}$

где $u\; \sim \; N\; (0,\; \sigma \; 2)\; \{\backslash \; displaystyle\; u\; \backslash \; sim\; N\; (0,\; \backslash \; sigma\; ^\; \{2\})\}$- это термин ошибки. В модели женщина = 1, когда человек - женщина, и женщина = 0, когда человек мужчина. $\delta \; 0\; \{\backslash \; displaystyle\; \backslash \; delta\; \_\; \{0\}\}$можно интерпретировать как разницу в заработной плате между мужчинами и женщинами при неизменном уровне образования. Таким образом, δ 0 помогает определить, существует ли дискриминация в оплате труда между мужчинами и женщинами. Например, если δ 0>0 (положительный коэффициент), то женщины получают более высокую заработную плату, чем мужчины (при сохранении других факторов постоянными). Коэффициенты, прикрепленные к фиктивным переменным, называются коэффициентами дифференциального пересечения . Модель можно изобразить графически как перехватывающий сдвиг между самками и самцами. На рисунке случай δ 0<0 is shown (wherein men earn a higher wage than women).

фиктивных переменных можно распространить на более сложные случаи. Например, сезонные эффекты могут быть зафиксированы путем создания фиктивных переменных для каждого из сезонов: $D\; 1\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{1\}\; =\; 1\}$, если наблюдение предназначено для лета, и равно ноль в противном случае; $D\; 2\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{2\}\; =\; 1\}$тогда и только тогда, когда осень, иначе равняется нулю; $D\; 3\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{3\}\; =\; 1\}$тогда и только тогда, когда зима, иначе равно нулю; и $D\; 4\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{4\}\; =\; 1\}$тогда и только тогда, когда пружина, иначе равняется нулю. В панельных данных, оценки фиксированных эффектов создаются фиктивные переменные для каждой из единиц в перекрестных данных (например, фирм или стран) или периодов в объединенном Временные ряды. Однако в таких регрессиях необходимо удалить либо постоянный член , либо один из фиктивных элементов, при этом связанная с ним категория становится базовой категорией, по которой оцениваются другие, чтобы избежать ловушка фиктивной переменной :

Постоянный член во всех уравнениях регрессии - это коэффициент, умноженный на регрессор, равный единице. Когда регрессия выражается в виде матричного уравнения, матрица регрессоров состоит из столбца единиц (постоянный член), векторов нулей и единиц (фиктивные числа) и, возможно, других регрессоров. Если, скажем, включать в себя как мужские, так и женские манекены, сумма этих векторов является вектором единиц, поскольку каждое наблюдение классифицируется как мужское или женское. Таким образом, эта сумма равна регрессору постоянного члена, первому вектору единиц. В результате уравнение регрессии будет неразрешимым даже с помощью типичного псевдообратного метода. Другими словами: если присутствуют и регрессор вектора единиц (постоянный член), и исчерпывающий набор фиктивных переменных, возникает идеальная мультиколлинеарность, и система уравнений, образованная регрессией, не имеет уникального решение. Это называется ловушкой фиктивной переменной . Ловушки можно избежать, удалив либо постоянный член, либо один из вызывающих нарушение манекенов. Удаленный макет становится базовой категорией, с которой сравниваются другие категории.

Модель регрессии, в которой зависимая переменная является количественной по своей природе, но все независимые переменные являются фиктивными (качественными по своей природе), называется моделью дисперсионного анализа (ANOVA). 74>

Модель ANOVA с одной качественной переменной

Предположим, мы хотим провести регрессию, чтобы выяснить, различается ли средняя годовая зарплата учителей государственных школ в трех географических регионах в стране A с 51 штатом: (1) Север (21 штат) (2) Юг (17 штатов) (3) Запад (13 штатов). Предположим, что простая арифметическая средняя заработная плата выглядит следующим образом: 24 424,14 доллара (север), 22 894 доллара (юг), 26 158,62 доллара (запад). Среднеарифметические значения разные, но отличаются ли они друг от друга статистически? Для сравнения средних значений можно использовать методы дисперсионного анализа. Модель регрессии может быть определена как:

$Y\; i\; =\; \alpha \; 1\; +\; \alpha \; 2\; D\; 2\; i\; +\; \alpha \; 3\; D\; 3\; i\; +\; ui\; \{\backslash \; displaystyle\; Y\_\; \{i\}\; =\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; alpha\; \_\; \{2\; \}\; D\_\; \{2i\}\; +\; \backslash \; alpha\; \_\; \{3\}\; D\_\; \{3i\}\; +\; u\_\; \{i\}\}$,

где

$Y\; i\; =\; \{\backslash \; displaystyle\; Y\_\; \{i\}\; =\}$средняя годовая зарплата учителей государственных школ в штате i

$D\; 2\; i\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{2i\}\; =\; 1\}$, если штат i находится в Северном регионе

$D\; 2\; i\; =\; 0\; \{\backslash \; displaystyle\; D\_\; \{2i\}\; =\; 0\}$в противном случае (любой регион, кроме севера)

$D\; 3\; i\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{3i\}\; =\; 1\}$, если состояние i находится в Южном регионе

$D\; 3\; i\; =\; 0\; \{\backslash \; displaystyle\; D\_\; \{3i\}\; =\; 0\}$в противном случае

В этой модели у нас есть только качественные регрессоры, принимающие значение 1, если наблюдение относится к определенной категории и 0, если оно принадлежит к любой другой категории. Это делает его моделью ANOVA.

Рисунок 2: График, показывающий результаты регрессии на примере модели ANOVA: Средние годовые зарплаты учителей государственных школ в 3 регионах страны A.

Теперь, принимая ожидание обеих сторон, мы получите следующее:

Средняя заработная плата учителей государственных школ в Северном регионе:

E (Y i|D2i= 1, D 3i = 0) = α 1 + α 2

Средняя зарплата учителей государственных школ в Южном регионе:

E (Y i|D2i= 0, D 3i = 1) = α 1 + α 3

Средняя зарплата учителей государственных школ в Западном регионе:

E (Y i|D2i= 0, D 3i = 0) = α 1

(член ошибки не включаются в ожидаемые значения, поскольку предполагается, что он удовлетворяет обычным условиям OLS, т. е. E (u i) = 0)

Ожидаемые значения можно интерпретировать следующим образом: средняя зарплата учителей государственных школ на Западе равна члену пересечения α 1 в уравнении множественной регрессии и дифференциальным коэффициентам пересечения, α 2 и α 3, объяснять насколько средняя заработная плата учителей в Северном и Южном регионах отличается от заработной платы учителей на Западе. Таким образом, средняя зарплата учителей на Севере и Юге сравнивается со средней зарплатой учителей на Западе. Следовательно, Западный регион становится базовой группой или эталонной группой, то есть группой, с которой производятся сравнения. Пропущенная категория, то есть категория, которой не назначен никакой манекен, принимается в качестве категории базовой группы.

Используя указанные данные, результат регрессии будет:

Ŷi= 26,158,62 - 1734,473D 2i - 3264,615D 3i

se = (1128,523) (1435,953) (1499,615)

t = (23,1759) (-1,2078) (-2,1776)

p = (0,0000) (0,2330) (0,0349)

R = 0,0901

где, se = стандартная ошибка, t = t-статистика, p = p значение

Результат регрессии можно интерпретировать как: Средняя заработная плата учителей на Западе (базовая группа) составляет около 26 158 долларов, зарплата учителей на Севере ниже примерно на 1734 доллара (26 158,62 доллара - 1734 473 доллара = 24 424,14 доллара, что является средней зарплатой учителей на Севере), а зарплата учителей на Севере ниже. на юге она ниже примерно на 3265 долларов (26 158,62 доллара - 3264,615 доллара = 22 894 доллара, что является средней зарплатой учителей на Юге).

Чтобы выяснить, отличаются ли средние зарплаты учителей на Севере и Юге статистически от зарплат учителей на Западе (категория сравнения), мы должны выяснить, соответствуют ли коэффициенты наклона регрессии результат статистически значимый. Для этого нам нужно учитывать значения p. Расчетный коэффициент наклона для Севера не является статистически значимым, поскольку его значение p составляет 23 процента; однако показатель Юга статистически значим на уровне 5%, поскольку его значение p составляет всего около 3,5%. Таким образом, общий результат состоит в том, что средние зарплаты учителей на Западе и Севере статистически не отличаются друг от друга, но средняя заработная плата учителей на Юге статистически ниже, чем на Западе, примерно на 3265 долларов. Модель схематически показана на рисунке 2. Эта модель представляет собой модель ANOVA с одной качественной переменной, имеющей 3 категории.

Модель ANOVA с двумя качественными переменными

Предположим, мы рассматриваем модель ANOVA с двумя качественными переменными. переменные, каждая из которых разделена на две категории: почасовая оплата должна быть объяснена в терминах качественных переменных Семейное положение (женат / не женат) и географический регион (север / не-север). Здесь семейное положение и географический регион - две объяснительные фиктивные переменные.

Скажем, результат регрессии на основе некоторых заданных данных выглядит следующим образом:

Ŷi= 8,8148 + 1,0997D 2 - 1,6729D 3

где,

Y = почасовая оплата (в долларах)

D2= семейное положение, 1 = замужем, 0 = иначе

D3= географический регион, 1 = север, 0 = в противном случае

В этой модели каждой качественной переменной присваивается одна фиктивная переменная, на единицу меньше, чем количество категорий, включенных в каждую.

Здесь основная группа - это опущенная категория: не состоящие в браке, не-северные регионы (не состоящие в браке люди, которые не живут в северном регионе). Все сравнения будут проводиться по отношению к этой базовой группе или исключенной категории. Средняя почасовая оплата в базовой категории составляет около 8,81 доллара (условный член). Для сравнения, средняя почасовая оплата тех, кто состоит в браке, выше примерно на 1,10 доллара и составляет примерно 9,91 доллара (8,81 доллара + 1,10 доллара). Напротив, средняя почасовая оплата тех, кто живет на Севере, ниже примерно на 1,67 доллара и составляет примерно 7,14 доллара (8,81 доллара - 1,67 доллара).

Таким образом, если в регрессию включено несколько качественных переменных, важно отметить, что пропущенная категория должна быть выбрана в качестве эталонной категории, и все сравнения будут проводиться по отношению к этой категории. Член пересечения покажет ожидание для эталонной категории, а коэффициенты наклона покажут, насколько другие категории отличаются от эталонной (опущенной) категории.

Модель регрессии, которая содержит смесь количественных и качественных переменных, которая называется моделью анализа ковариации (ANCOVA). Модели ANCOVA являются расширением моделей ANOVA. Они статистически контролируют влияние количественных независимых переменных (также называемых ковариатами или контрольными переменными).

Чтобы проиллюстрировать, как качественные и количественные регрессоры включены в модели ANCOVA, предположим, что мы рассматриваем тот же пример, что и в модели ANOVA. с одной качественной переменной: среднегодовая зарплата учителей государственных школ в трех географических регионах страны A. Если мы включим в эту регрессию количественную переменную, расходы правительства штата на государственные школы на ученика, мы получим следующую модель:

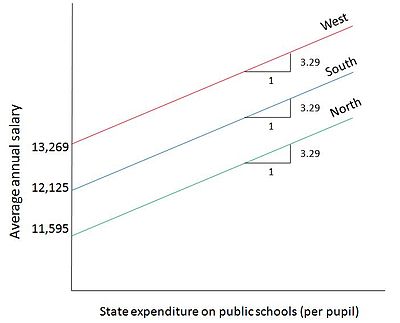Рисунок 3: График, показывающий результаты регрессии для примера модели ANCOVA: Заработная плата учителя государственной школы (Y) по отношению к государственным расходам на ученика в государственных школах.

Yi= α 1 + α 2D2i+ α 3D3i+ α 4Xi+ U i

, где

Yi= средняя годовая зарплата учителей государственных школ в штате i

Xi= государственные расходы на государственные школы на ученика

D2i= 1, если штат i находится в северном регионе

D2i= 0, в противном случае

D3i= 1, если состояние i находится в Южном регионе

D3i= 0, иначе

Скажем, результат регрессии для этой модели:

Ŷi= 13,269,11 - 1673,514D 2i - 1144,157D 3i + 3,2889 X i

Результат предполагает, что на каждое увеличение государственных расходов на одного ученика государственных школ на 1 доллар средняя зарплата учителя государственной школы увеличивается примерно на 3,29 доллара. Кроме того, для штата в Северном регионе средняя зарплата учителей ниже, чем в Западном регионе, примерно на 1673 доллара, а для штата в Южном регионе средняя заработная плата учителей ниже, чем в Западном регионе, примерно на 1144 долларов. На рисунке 3 схематически изображена эта модель. Строки средней заработной платы параллельны друг другу, исходя из предположения модели, что коэффициент расходов не зависит от штата. Компромисс, показанный отдельно на графике для каждой категории, находится между двумя количественными переменными: заработная плата учителей государственных школ (Y) по отношению к государственным расходам на ученика в государственных школах (X).

Количественные регрессоры в регрессионных моделях часто взаимодействуют друг с другом. Таким же образом качественные регрессоры или фиктивные переменные также могут иметь эффекты взаимодействия друг с другом, и эти взаимодействия могут быть изображены в регрессионной модели. Например, в регрессии, включающей определение заработной платы, если рассматривать две качественные переменные, а именно пол и семейное положение, может существовать взаимосвязь между семейным положением и полом. Эти взаимодействия можно показать в уравнении регрессии, как показано в примере ниже.

Если двумя качественными переменными являются пол и семейное положение, а количественным показателем является количество лет образования, то чисто линейная регрессия в объяснителях будет

Yi= β 1 + β 2D2, i + β 3D3, i + αX i + U i

, где

i обозначает конкретное лицо

Y = ежечасно Заработная плата (в долларах США)

X = количество лет обучения

D2= 1, если женщина, 0 в противном случае

D3= 1, если замужем, 0 в противном случае

Эта спецификация не учитывает возможность взаимодействия которое происходит между двумя качественными переменными, D 2 и D 3. Например, замужняя женщина может получать заработную плату, отличную от заработной платы не состоящего в браке мужчины, на сумму, не равную сумме разницы в том, что она исключительно женщина и единолично состоит в браке. Тогда влияние взаимодействующих манекенов на среднее значение Y не просто аддитивное, как в случае вышеприведенной спецификации, но также мультипликативное, и определение заработной платы может быть определено как:

Yi= β 1 + β 2D2, i + β 3D3, i + β 4(D2, i D 3, i) + αX i + U i

Здесь

β2= дифференциальный эффект женского пола

β3= дифференциальный эффект женатого брака

β4= дополнительный дифференциальный эффект женского и женского брака

Согласно этому уравнению, при отсутствии ненулевой ошибки заработная плата не состоящего в браке мужчины составляет β 1 + αX i, а заработная плата незамужней женщины составляет β 1 + β 2 + αX i, то для женатого мужчины β 1 + β 3 + αX i, а замужняя женщина - β 1 + β 2 + β 3 + β 4 + αX i (где любая из оценок коэффициентов манекенов могла оказаться положительной, нулевой или отрицательной).

Таким образом, макет взаимодействия (продукт двух макетов) может изменить зависимую переменную от значения, которое он получает, когда два макета рассматриваются по отдельности.

Однако использование продуктов макета переменных для фиксации взаимодействий можно избежать, используя другую схему категоризации данных - ту, которая определяет категории с точки зрения комбинаций характеристик. Если мы допустим

D4= 1, если женщина незамужняя, 0 в противном случае

D5= 1, если замужняя женщина, 0 в противном случае

D6= 1, если замужняя женщина, 0 в противном случае

, тогда достаточно указать регрессию

Yi= δ 1 + δ 4D4, i + δ 5D5, i + δ 6D6, i + αX i + U i.

Тогда при нулевом шоковом члене значение зависимой переменной будет δ 1 + αX i для базовой категории неженатых мужчин, δ 1 + δ 4 + αX i для незамужних женщин, δ 1 + δ 5 + αX i для замужних мужчин и δ 1 + δ 6 + αX i для замужних женщин. Эта спецификация включает такое же количество переменных с правой стороны, что и предыдущая спецификация с термином взаимодействия, и результаты регрессии для прогнозируемого значения зависимой переменной, зависящей от X i, для любой комбинации качественных признаков., идентичны между этой спецификацией и спецификацией взаимодействия.

Что произойдет, если зависимая переменная - фиктивная?

Модель с фиктивной зависимой переменной (также известной как качественная зависимая переменная) - это модель, в которой зависимая переменная, на которую влияют независимые переменные, носит качественный характер. Некоторые решения относительно того, «сколько» действия должно быть выполнено, требуют предварительного принятия решения о том, выполнять действие или нет. Например, количество продукции, которую необходимо произвести, затраты, которые должны быть понесены, и т. Д. Включают предварительные решения о том, производить или нет, тратить или нет и т. Д. Такие «предыдущие решения» становятся зависимыми фикциями в регрессионной модели. 74>

Например, решение работника стать частью рабочей силы становится фиктивной зависимой переменной. Решение является дихотомическим, то есть решение имеет два возможных результата: да и нет. Таким образом, зависимая фиктивная переменная «Участие» примет значение 1, если участвует, и 0, если не участвует. Некоторые другие примеры дихотомических зависимых манекенов приведены ниже:

Решение: Выбор профессии. Зависимый манекен: Супервизор = 1, если супервизор, 0, если не супервизор.

Решение: Принадлежность к политической партии. Зависимый пустышка: Принадлежность = 1, если связана с стороной, 0, если не аффилирована.

Решение: Выход на пенсию. Зависимый манекен: На пенсии = 1, если на пенсии, 0, если не на пенсии.

Когда качественная зависимая фиктивная переменная имеет более двух значений (например, принадлежность ко многим политическим партиям), она становится мультиответной, мультиномиальной или полихотомической моделью.

Модели зависимых фиктивных переменных

Анализ моделей зависимых фиктивных переменных может выполняться различными методами. Одним из таких методов является обычный метод OLS, который в этом контексте называется линейной вероятностной моделью. Альтернативный метод состоит в том, чтобы предположить, что существует ненаблюдаемая непрерывная скрытая переменная Y и что наблюдаемая дихотомическая переменная Y = 1, если Y>0, 0 в противном случае. Это основная концепция моделей logit и probit. Эти модели кратко обсуждаются ниже.

Линейная вероятностная модель

Обычная модель наименьших квадратов, в которой зависимая переменная Y является дихотомической фиктивной переменной, принимающей значения 0 и 1, - это линейная вероятностная модель (LPM). Предположим, мы рассматриваем следующую регрессию:

$Y\; i\; =\; \alpha \; 1\; +\; \alpha \; 2\; X\; i\; +\; ui\; \{\backslash \; displaystyle\; Y\_\; \{i\}\; =\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; alpha\; \_\; \{2\}\; X\_\; \{i\}\; +\; u\_\; \{\; i\}\}$

где

$X\; \{\backslash \; displaystyle\; X\}$= доход семьи

$Y\; =\; 1\; \{\backslash \; displaystyle\; Y\; =\; 1\}$, если дом принадлежит семья, 0, если дом не принадлежит семье

Модель называется линейной вероятностной моделью, потому что регрессия является линейной. условное среднее Y i для данного X i, записанное как $E\; (Y\; i\; |\; X\; i)\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{E\}\; (\; Y\_\; \{i\}\; |\; X\_\; \{i\})\}$, интерпретируется как условная вероятность того, что событие произойдет для этого значения X i - то есть, Pr (Y i = 1 | X i). В этом примере $E\; (Y\; i\; |\; X\; i)\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{E\}\; (Y\_\; \{i\}\; |\; X\_\; \{i\})\}$дает вероятность того, что дом принадлежит семья, доход которой определяется как X i.

Теперь, используя предположение OLS, $E\; (ui\; |\; X\; i)\; =\; 0\; \{\backslash \; displaystyle\; E\; (u\_\; \{i\}\; |\; X\_\; \{i\})\; =\; 0\}$, получаем

$E\; (Y\; i\; |\; X\; i)\; =\; \alpha \; 1\; +\; \alpha \; 2\; X\; i\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{E\}\; (Y\_\; \{i\}\; |\; X\_\; \{i\})\; =\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; alpha\; \_\; \{2\}\; X\_\; \{i\}\}$

Некоторые проблемы присущи модели LPM:

1. Линия регрессии не будет хорошо подогнанной one и, следовательно, меры значимости, такие как R, не будут надежными.
2. Модели, анализируемые с использованием подхода LPM, будут иметь гетероскедастические нарушения.
3. Член ошибки будет иметь ненормальное распределение.
4. LPM может давать предсказанные значения зависимой переменной, которые больше 1 или меньше 0. Это будет трудно интерпретировать, поскольку предсказанные значения предназначены для вероятностей, который должен находиться в диапазоне от 0 до 1.
5. Могут существовать st нелинейная связь между переменными модели LPM, и в этом случае линейная регрессия не будет точно соответствовать данным.

Альтернативы LPM

Рисунок 4: Кумулятивная функция распределения.

Чтобы избежать Из-за ограничений LPM необходима модель, в которой в качестве объясняющей переменной X i увеличивается P i = E (Y i = 1 | X i) должен оставаться в диапазоне от 0 до 1. Таким образом, отношения между независимыми и зависимыми переменными обязательно нелинейны.

Для этой цели кумулятивная функция распределения (CDF) может использоваться для оценки регрессии зависимой фиктивной переменной. На рисунке 4 показана S-образная кривая, напоминающая CDF случайной величины. В этой модели вероятность находится между 0 и 1, и нелинейность была зафиксирована. Теперь стоит вопрос о выборе CDF, который будет использоваться.

Могут использоваться две альтернативные CDF: логистическая и нормальная CDF. Логистическая CDF приводит к модели логита, а нормальная CDF дает начало модели пробит.

модель логита

Недостатки LPM привели к разработке более доработанная и улучшенная модель называется логит-моделью. В логит-модели кумулятивное распределение члена ошибки в уравнении регрессии является логистическим. Регрессия более реалистична, поскольку она нелинейна.

Логит-модель оценивается с использованием метода максимального правдоподобия. В этой модели $P\; (Y\; =\; 1\; |\; X)\; \{\backslash \; displaystyle\; P\; (Y\; =\; 1\; |\; X)\}\;$, что представляет собой вероятность того, что зависимая переменная примет значение 1 с учетом независимого переменная:

$P\; i\; =\; 1\; 1\; +\; e\; -\; zi\; =\; ezi\; 1\; +\; ezi\; \{\backslash \; displaystyle\; P\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{1\; +\; e\; ^\; \{-\; z\_\; \{i\}\}\}\}\; \backslash \; =\; \{\backslash \; гидроразрыва\; \{е\; ^\; \{z\_\; \{i\}\}\}\; \{1\; +\; e\; ^\; \{z\_\; \{i\}\}\}\}\; \backslash \}$

где $zi\; =\; \alpha \; 1\; +\; \alpha \; 2\; X\; i\; +\; ui\; \{\backslash \; displaystyle\; z\_\; \{i\}\; =\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; alpha\; \_\; \{2\}\; X\_\; \{i\}\; +\; u\_\; \{i\}\}$.

Затем модель выражается в виде отношения шансов : что моделируется в логистической регрессии как натуральный логарифм шансов, причем шансы определяются как $P\; /\; (1\; -\; P)\; \{\backslash \; displaystyle\; P\; /\; (1-P)\}$. Принимая натуральный логарифм шансов, логит (L i) выражается как

$L\; i\; =\; ln\; \; (P\; i\; 1\; -\; P\; i)\; =\; z\; i\; =\; \alpha \; 1\; +\; \alpha \; 2\; X\; i.\; \{\backslash \; displaystyle\; L\_\; \{i\}\; =\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{P\_\; \{i\}\}\; \{1-P\_\; \{i\}\}\}\; \backslash \; right)\; =\; z\_\; \{i\}\; =\; \backslash \; alpha\; \_\; \{1\}\; +\; \backslash \; alpha\; \_\; \{2\}\; X\_\; \{i\}.\}$

Это соотношение показывает, что L i линейно по отношению к X i, но вероятности не линейны в терминах X i.

Пробит-модель

Еще одна модель, которая была разработана, чтобы компенсировать недостатки LPM, - это пробит-модель. Пробит-модель использует тот же подход к нелинейности, что и логит-модель; однако он использует обычный CDF вместо логистического CDF.

• Двоичная регрессия
• Тест Чоу
• Проверка гипотез
• Индикаторная функция
• Линейная дискриминантная функция
• Мультиколлинеарность

• Asteriou, Dimitrios; Холл, С.Г. (2015). "Фиктивные переменные". Прикладная эконометрика (3-е изд.). Лондон: Пэлгрейв Макмиллан. С. 209–230. ISBN 978-1-137-41546-2.
• Койман, Мариус А. (1976). Фиктивные переменные в эконометрике. Тилбург: Издательство Тилбургского университета. ISBN 90-237-2919-6.

Викиверситет содержит учебные ресурсы по фиктивной переменной (статистика)

• Маатуис, Марло (2007). «Глава 7: Регрессия фиктивной переменной» (PDF). Stat 423: Прикладная регрессия и дисперсионный анализ. Архивировано из оригинального (PDF) 16 декабря 2011 года.
• Фокс, Джон (2010). «Регрессия фиктивной переменной» (PDF).
• Бейкер, Сэмюэл Л. (2006). «Фиктивные переменные» (PDF). Архивировано из оригинального (PDF) 1 марта 2006 г.