Гетероскедастичность

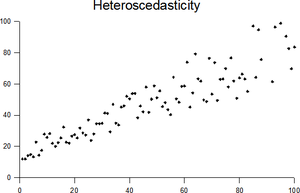
График со случайными данными, показывающими гетероскедастичность

В статистике вектор случайных величин - это гетероскедастический (или гетероскедастический ; от древнегреческий гетеро «разный» и скедасис «дисперсия»), если изменчивость случайного нарушения отличается для разных элементов вектора. Здесь изменчивость может быть определена количественно с помощью дисперсии или любой другой меры статистической дисперсии. Таким образом, гетероскедастичность - это отсутствие гомоскедастичности. Типичный пример - совокупность наблюдений за доходами в разных городах.

Существование гетероскедастичности является серьезной проблемой в регрессионном анализе и дисперсионном анализе, поскольку оно делает недействительными статистические тесты значимости, предполагающие что ошибки моделирования имеют одинаковую дисперсию. Хотя обычная оценка методом наименьших квадратов все еще несмещена при наличии гетероскедастичности, она неэффективна, и вместо нее следует использовать обобщенный метод наименьших квадратов.

Поскольку гетероскедастичность касается ожидания второго момента ошибок, его наличие упоминается как неправильная спецификация второго порядка.

эконометрист Роберт Энгл получил в 2003 г. Нобелевскую премию по экономике за свои исследования регрессионного анализа в присутствии гетероскедастичности, что привело к его формулировке метод моделирования авторегрессионной условной гетероскедастичности (ARCH).

• 1 Определение
• 2 Последствия
• 3 Обнаружение
• 4 Исправления
• 5 Примеры
• 6 Многомерный случай
• 7 Примечания
• 8 Ссылки
• 9 Дополнительная литература
• 10 Внешние ссылки

Рассмотрим уравнение регрессии $yi\; =\; xi\; \beta \; +\; ϵ\; i,\; i\; =\; 1,\dots ,\; N,\; \{\backslash \; Displaystyle\; у\_\; \{я\}\; =\; х\_\; \{я\; \}\; \backslash \; beta\; +\; \backslash \; epsilon\; \_\; \{i\},\; i\; =\; 1,\; \backslash \; ldots,\; N,\}$где зависимая случайная величина $yi\; \{\backslash \; displaystyle\; y\_\; \{i\}\}$равна детерминированной переменной $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$, умноженной на коэффициент $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$плюс член случайного возмущения $ϵ\; i\; \{\backslash \; displaystyle\; \backslash \; epsilon\; \_\; \{i\}\}$с нулевым средним значением. Нарушения гомоскедастичны, если дисперсия $ϵ\; i\; \{\backslash \; displaystyle\; \backslash \; epsilon\; \_\; \{i\}\}$является константой $\sigma \; 2\; \{\backslash \; displaystyle\; \backslash \; sigma\; ^\; \{2\}\}$; в противном случае они гетероскедастичны. В частности, возмущения являются гетероскедастическими, если дисперсия $ϵ\; i\; \{\backslash \; displaystyle\; \backslash \; epsilon\; \_\; \{i\}\}$зависит от i или от значения $xi\; \{\backslash \; displaystyle\; x\_\; \{i\; \}\}$. Один из способов, которым они могут быть гетероскедастичны, - это если $\sigma \; i\; 2\; =\; xi\; \sigma \; 2\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{i\}\; ^\; \{2\}\; =\; x\_\; \{i\}\; \backslash \; sigma\; ^\; \{2\}\}$( пример scedastic функции ), поэтому дисперсия пропорциональна значению x.

В более общем смысле, если матрица дисперсии-ковариации возмущений $ϵ\; i\; \{\backslash \; displaystyle\; \backslash \; epsilon\; \_\; \{i\}\}$по i имеет непостоянную диагональ, возмущение является гетероскедастическим. Приведенные ниже матрицы представляют собой ковариации, когда есть всего три наблюдения во времени. Нарушение в матрице A гомоскедастично; это простой случай, когда OLS - лучшая линейная несмещенная оценка. Возмущения в матрицах B и C гетероскедастичны. В матрице B дисперсия изменяется во времени, неуклонно увеличиваясь во времени; в матрице C дисперсия зависит от значения x. Нарушение в матрице D гомоскедастично, потому что диагональные дисперсии постоянны, даже если недиагональные ковариации не равны нулю, а метод наименьших квадратов неэффективен по другой причине: последовательная корреляция.

$A\; =\; \sigma \; 2\; [1\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 1]\; B\; =\; \sigma \; 2\; [1\; 0\; 0\; 0\; 2\; 0\; 0\; 0\; 3]\; C\; =\; \sigma \; 2\; [x\; 1\; 0\; 0\; 0\; x\; 2\; 0\; 0\; 0\; x\; 3\; ]\; D\; знак\; равно\; \sigma \; 2\; [1\; \rho \; \rho \; 2\; \rho \; 1\; \rho \; \rho \; 2\; \rho \; 1]\; \{\backslash \; displaystyle\; A\; =\; \backslash \; sigma\; ^\; \{2\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; B\; =\; \backslash \; sigma\; ^\; \{2\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 0\; 2\; 0\; \backslash \backslash \; 0\; 0\; 3\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash \; ;\; \backslash ;\; \backslash ;\; \backslash ;\; C\; =\; \backslash \; sigma\; ^\; \{2\}\; \{\backslash \; begin\; \{bmatrix\}\; x\_\; \{1\}\; 0\; 0\; \backslash \backslash \; 0\; x\_\; \{2\}\; 0\; \backslash \backslash \; 0\; 0\; x\_\; \{3\}\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash ;\; \backslash \; ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; D\; =\; \backslash \; sigma\; ^\; \{2\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \; rho\; \backslash \; rho\; ^\; \{2\}\; \backslash \backslash \backslash \; rho\; 1\; \backslash \; rho\; \backslash \backslash \backslash \; rho\; ^\; \{2\}\; \backslash \; rho\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\}$

Одно из допущений классической модели линейной регрессии - отсутствие гетероскедастичности. Нарушение этого предположения означает, что теорема Гаусса – Маркова неприменима, а это означает, что оценки OLS не являются Лучшими линейными несмещенными оценками (СИНИЙ), а их дисперсия равна не самый низкий из всех других объективных оценок. Гетероскедастичность не вызывает смещения обычных оценок коэффициентов методом наименьших квадратов, хотя может привести к смещению обычных оценок дисперсии (и, следовательно, стандартных ошибок) коэффициентов методом наименьших квадратов, возможно, выше или ниже истинной дисперсии или дисперсии генеральной совокупности. Таким образом, регрессионный анализ с использованием гетероскедастических данных по-прежнему будет обеспечивать беспристрастную оценку взаимосвязи между переменной-предиктором и результатом, но стандартные ошибки и, следовательно, выводы, полученные на основе анализа данных, вызывают подозрение. Предвзятые стандартные ошибки приводят к необъективным выводам, поэтому результаты проверки гипотез могут быть неверными. Например, если OLS выполняется на гетероскедастическом наборе данных, что дает предвзятую оценку стандартной ошибки, исследователь может не отклонить нулевую гипотезу на заданном уровне значимости , когда эта нулевая гипотеза на самом деле нехарактерна для действительной население (с ошибкой типа II ).

При определенных допущениях, МНК-оценка имеет нормальное асимптотическое распределение при правильной нормализации и центрировании (даже если данные не получены из нормального распределения ). Этот результат используется для обоснования с использованием нормального распределения или распределения хи-квадрат (в зависимости от того, как вычисляется тестовая статистика ) при проведении проверки гипотез. Это справедливо даже при гетероскедастичности. Точнее, оценка МНК при наличии гетероскедастичности является асимптотически нормальной при правильной нормировке и центрировании с матрицей дисперсии-ковариации , которая отличается от случая гомоскедастичности. В 1980 году Уайт предложил согласованную оценку для ковариационно-дисперсионной матрицы асимптотического распределения оценки OLS. Это подтверждает использование проверки гипотез с использованием оценок OLS и оценки дисперсии-ковариации Уайта при гетероскедастичности.

Гетероскедастичность также является важной практической проблемой, возникающей в задачах ANOVA. F-тест все еще может использоваться в некоторых обстоятельствах.

Однако было сказано, что студенты, изучающие эконометрику, не должны слишком остро реагировать на гетероскедастичность. Один автор написал: «Неравномерная дисперсия ошибок стоит исправлять только тогда, когда проблема серьезна». Кроме того, еще одно предостережение было в форме: «гетероскедастичность никогда не была причиной для отказа от хорошей модели». С появлением стандартных ошибок, согласованных с гетероскедастичностью, позволяющих делать выводы без указания условного второго момента ошибки, проверка условной гомоскедастичности стала не такой важной, как в прошлом.

Для любых не- линейная модель (например, модели Logit и Probit ), однако гетероскедастичность имеет более серьезные последствия: оценки максимального правдоподобия (MLE) параметров будут смещены, а также непоследовательны (если функция правдоподобия не изменена для правильного учета точной формы гетероскедастичности). Тем не менее, в контексте моделей бинарного выбора (Logit или Probit ) гетероскедастичность приведет только к положительному эффекту масштабирования на асимптотическое среднее значение неправильно заданной MLE (т. Е. Модели, которая игнорирует гетероскедастичность). В результате прогнозы, основанные на неверно заданном MLE, останутся верными. Кроме того, неправильно указанные Probit и Logit MLE будут асимптотически нормально распределены, что позволяет выполнять обычные тесты значимости (с соответствующей матрицей дисперсии-ковариации). Однако, что касается проверки общей гипотезы, как указано Грин, «простое вычисление устойчивой ковариационной матрицы для несовместимой в остальном оценки не дает ей оправдания. Следовательно, достоинства надежной ковариационной матрицы в этой настройке неясны ».

Абсолютное значение остатков для смоделированных гетероскедастических данных первого порядка

Существует несколько методов проверки наличия гетероскедастичности. Хотя тесты на гетероскедастичность между группами формально можно рассматривать как частный случай тестирования в рамках регрессионных моделей, некоторые тесты имеют структуру, специфичную для этого случая.

Тесты регрессии

• Тест Левена
• Тест Голдфельда – Квандта
• Тест Парка
• Тест Глейзера
• Тест Брауна – Форсайта
• Тест Бреуша – Пагана
• Тест Уайта
• Тест Кука – Вайсберга

Тесты для сгруппированных данных

• F-тест равенства дисперсий
• C-тест Кохрана
• Тест Хартли

Эти тесты состоят из тестовой статистики (a математическое выражение, дающее числовое значение как функцию данных), гипотезу, которая будет проверяться (нулевая гипотеза ), альтернативная гипотеза и утверждение о распределении статистики при нулевой гипотезе.

Многие вводные книги по статистике и эконометрике, по педагогическим причинам, представляют эти тесты в предположении, что набор данных взят из нормального распределения. Большое заблуждение заключается в том, что это предположение необходимо. Большинство описанных выше методов обнаружения гетероскедастичности можно модифицировать для использования, даже если данные получены не из нормального распределения. Во многих случаях это предположение может быть ослаблено, давая тестовую процедуру, основанную на той же или аналогичной тестовой статистике, но с распределением при нулевой гипотезе, оцененным альтернативными способами: например, с использованием асимптотических распределений, которые могут можно получить из асимптотической теории или с помощью повторной выборки.

Есть четыре общих поправки на гетероскедастичность. Это:

• Просмотр логарифмированных данных. Нелогарифмированные ряды, которые растут экспоненциально, часто имеют увеличивающуюся изменчивость по мере того, как ряды растут с течением времени. Однако вариативность в процентах может быть довольно стабильной.
• Используйте другую спецификацию для модели (другие переменные X или, возможно, нелинейные преобразования переменных X).
• Применить метод оценки взвешенных наименьших квадратов, в котором OLS применяется к преобразованным или взвешенным значениям X и Y. Веса варьируются в зависимости от наблюдений, обычно в зависимости от изменяющейся дисперсии ошибок. В одном варианте веса напрямую связаны с величиной зависимой переменной, и это соответствует процентной регрессии методом наименьших квадратов.
• Стандартные ошибки, согласованные с гетероскедастичностью, (HCSE), хотя и смещены, но улучшают оценки OLS. HCSE - это последовательная оценка стандартных ошибок в регрессионных моделях с гетероскедастичностью. Этот метод корректирует гетероскедастичность без изменения значений коэффициентов. Этот метод может быть лучше обычного OLS, потому что, если присутствует гетероскедастичность, он исправляет ее, однако, если данные гомоскедастичны, стандартные ошибки эквивалентны стандартным стандартным ошибкам, оцененным с помощью OLS. Несколько модификаций метода Уайта для вычисления стандартных ошибок, согласующихся с гетероскедастичностью, были предложены как поправки с превосходными свойствами конечной выборки.
• Используйте MINQUE или даже обычные оценки $si\; 2\; =\; (\; ni\; -\; 1)\; -\; 1\; \sum \; j\; (yij\; -\; y\; ¯\; i)\; 2\; \{\backslash \; displaystyle\; s\_\; \{i\}\; ^\; \{2\}\; =\; (n\_\; \{i\}\; -1)\; ^\; \{-\; 1\}\; \backslash \; sum\; \_\; \{j\}\; (y\_\; \{\; ij\}\; -\; \{\backslash \; bar\; \{y\}\}\; \_\; \{i\})\; ^\; \{2\}\}$(для $i\; =\; 1,\; 2,...,\; k\; \{\backslash \; displaystyle\; i\; =\; 1,2,...,\; k\}$независимых выборок с $j\; =\; 1,\; 2,...,\; ni\; \{\backslash \; displaystyle\; j\; =\; 1,2,...,\; n\_\; \{i\}\}$наблюдений каждый), потери эффективности которых несущественны при большом количестве наблюдений на выборку ($ni>5\; \{\backslash \; displaystyle\; n\_\; \{i\}>5\}$), особенно для небольшого количества независимых образцов. 230>Примеры