Дельта-потенциал

Модель энергетического потенциала в квантовой механике

В квантовой механике дельта-потенциал представляет собой потенциальную яму, математически описываемую дельта-функцией Дирака - обобщенной функцией. Качественно он соответствует потенциалу, который везде равен нулю, кроме единственной точки, где он принимает бесконечное значение. Это можно использовать для моделирования ситуаций, когда частица может свободно перемещаться в двух областях пространства с барьером между двумя областями. Например, электрон может почти свободно перемещаться в проводящем материале, но если две проводящие поверхности расположены близко друг к другу, граница раздела между ними действует как барьер для электрона, который можно аппроксимировать дельта-потенциалом.

Дельта-потенциальная яма - это предельный случай конечной потенциальной ямы, который получается, если выдерживать произведение ширины ямы и постоянной потенциала при уменьшении ширины ямы и увеличении потенциала.

В этой статье для простоты рассматривается только одномерная потенциальная яма, но анализ можно расширить до других измерений.

• 1 Единичный дельта-потенциал
  • 1.1 Решение уравнения Шредингера
  • 1.2 Связанное состояние (E < 0)
  • _0) ">1.3 Рассеяние (E>0)
  • 1.4 Замечания и применение
• 2 Двойной дельта-потенциал
• 3 См. Также
• 4 Ссылки
• 5 Внешние ссылки

Не зависящее от времени уравнение Шредингера для волновой функции ψ (x) частицы в одном измерении в потенциале V (x) равно

$-\; \hslash \; 2\; 2\; md\; 2\; \psi \; dx\; 2\; (x)\; +\; V\; (x)\; \psi \; (x)\; Знак\; равно\; Е\; \psi \; (х),\; \{\backslash \; Displaystyle\; -\; \{\backslash \; гидроразрыва\; \{\backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; \{\backslash \; гидроразрыва\; \{d\; ^\; \{2\}\; \backslash \; psi\}\; \{dx\; ^\; \{2\}\}\}\; (х)\; +\; V\; (x)\; \backslash \; psi\; (x)\; =\; E\; \backslash \; psi\; (x)\; ~,\}$

где ħ - приведенная постоянная Планка, а E - энергия частицы

Дельта-потенциал - это потенциал

$V\; (x)\; =\; \lambda \; \delta \; (x),\; \{\backslash \; displaystyle\; \backslash \; displaystyle\; V\; (x)\; =\; \backslash \; lambda\; \backslash \; delta\; (x)\; ~,\}$

где δ (x) - дельта-функция Дирака..

Это называется дельта-потенциальной ямой, если λ отрицательно, и дельта-потенциальным барьером, если λ положительно. оштрафован на происхождение для простоты; сдвиг аргумента дельта-функции не меняет никаких результатов обработки.

Решение уравнения Шредингера

Потенциал разделяет пространство на две части (x < 0 and x>0). В каждой из этих частей потенциальная энергия равна нулю, и уравнение Шредингера сводится к

$d\; 2\; \psi \; d\; x\; 2\; =\; -\; 2\; m\; E\; \hslash \; 2\; \psi ;\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; psi\}\; \{dx\; ^\; \{2\}\}\}\; =\; -\; \{\backslash \; frac\; \{2mE\}\; \{\backslash \; hbar\; ^\; \{2\}\}\}\; \backslash \; psi\; ~;\}$

это линейное дифференциальное уравнение с постоянными коэффициентами, решениями которого являются линейные комбинации e и e, где волновое число k связано с энергии на

$k\; =\; 2\; m\; E\; \hslash .\; \{\backslash \; displaystyle\; k\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2mE\}\}\; \{\backslash \; hbar\}\}\; ~.\}$

В общем, из-за наличия дельта-потенциала в начале координат коэффициенты решения не обязательно должны быть то же самое в обоих полупространствах:

где в случае положительных энергий (действительный k), e представляет волну, бегущую вправо, а e - влево..

Можно получить соотношение между коэффициентами, наложив, что волновая функция будет непрерывной в начале координат,

$\psi \; (0)\; =\; \psi \; L\; (0)\; =\; \psi \; R\; (0)\; =\; A\; r\; +\; A\; l\; Знак\; равно\; В\; р\; +\; В\; l,\; \{\backslash \; Displaystyle\; \backslash \; psi\; (0)\; =\; \backslash \; psi\; \_\; \{L\}\; (0)\; =\; \backslash \; psi\; \_\; \{R\}\; (0)\; =\; A\_\; \{r\}\; +\; A\_\; \{l\}\; =\; B\_\; \{r\}\; +\; B\_\; \{l\}\; ~,\}$

Второе отношение ca n можно найти, изучая производную волновой функции. Обычно мы также можем наложить дифференцируемость в начале координат, но это невозможно из-за дельта-потенциала. Однако, если мы проинтегрируем уравнение Шредингера вокруг x = 0, на интервале [−ε, + ε]:

$-\; \hslash \; 2\; 2\; m\; \int \; -\; ϵ\; +\; ϵ\; \psi \; ″\; (x)\; dx\; +\; \int \; -\; ϵ\; +\; ϵ\; V\; (x)\; \psi \; (x)\; dx\; =\; E\; \int \; -\; ϵ\; +\; ϵ\; \psi \; (x)\; dx.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{\backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; epsilon\}\; ^\; \{+\; \backslash \; epsilon\}\; \backslash \; psi\; \text{'}\text{'}\; (x)\; \backslash ,\; dx\; +\; \backslash \; int\; \_\; \{-\; \backslash \; epsilon\; \}\; ^\; \{+\; \backslash \; epsilon\}\; V\; (x)\; \backslash \; psi\; (x)\; \backslash ,\; dx\; =\; E\; \backslash \; int\; \_\; \{-\; \backslash \; epsilon\}\; ^\; \{+\; \backslash \; epsilon\}\; \backslash \; psi\; (x)\; \backslash ,\; dx.\}$

В предел при ε → 0, правая часть этого уравнения обращается в нуль; левая сторона становится

$-\; \hslash \; 2\; 2\; m\; [\psi \; R\; \prime \; (0)\; -\; \psi \; L\; \prime \; (0)]\; +\; \lambda \; \psi \; (0),\; \{\backslash \; displaystyle\; \backslash \; textstyle\; -\; \{\backslash \; frac\; \{\backslash \; hbar\; ^\; \{\; 2\}\}\; \{2m\}\}\; [\backslash \; psi\; \text{'}\_\; \{R\}\; (0)\; -\; \backslash \; psi\text{'}\; \_\; \{L\}\; (0)]\; +\; \backslash \; lambda\; \backslash \; psi\; (0),\}$

потому что

$\int \; -\; ϵ\; +\; ϵ\; \psi \; ″\; (x)\; dx\; =\; [\psi \; \prime \; (+\; ϵ)\; -\; \psi \; \prime \; (-\; ϵ)].\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; epsilon\}\; ^\; \{+\; \backslash \; epsilon\}\; \backslash \; psi\; \text{'}\text{'}\; (x)\; \backslash ,\; dx\; =\; [\backslash \; psi\; \text{'}(\{+\; \backslash \; epsilon\})\; -\; \backslash \; psi\text{'}\; (\{-\; \backslash \; epsilon\})\; ].\}$

Подставляя определение ψ в это выражение, получаем

$-\; \hslash \; 2\; 2\; mik\; (-\; A\; r\; +\; A\; l\; +\; B\; r\; -\; B\; l)\; +\; \lambda \; (A\; r\; +\; A\; l)\; =\; 0.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{\backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; ik\; (-A\_\; \{r\}\; +\; A\_\; \{l\}\; +\; B\_\; \{r\}\; -B\_\; \{l\})\; +\; \backslash \; lambda\; (A\_\; \{r\}\; +\; A\_\; \{l\})\; =\; 0\; ~.\}$

Таким образом, граничные условия дают следующие ограничения на коэффициенты

$\{A\; r\; +\; A\; l\; -\; B\; r\; -\; B\; l\; =\; 0;\; -\; A\; r\; +\; A\; l\; +\; B\; r\; -\; B\; l\; знак\; равно\; 2\; m\; \lambda \; i\; k\; \hslash \; 2\; (A\; r\; +\; A\; l).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; A\_\; \{r\}\; +\; A\_\; \{l\}\; -B\_\; \{r\}\; -B\_\; \{l\}\; =\; 0;\; \backslash \backslash \; -\; A\_\; \{r\}\; +\; A\_\; \{l\}\; +\; B\_\; \{r\}\; -\; B\_\; \{l\}\; =\; \{\backslash \; frac\; \{2m\; \backslash \; lambda\}\; \{ik\; \backslash \; hbar\; ^\; \{2\}\}\}\; (A\_\; \{r\}\; +\; A\_\; \{l\})\; ~.\; \backslash \; End\; \{ases\}\}\}$

Связанное состояние ( E < 0)

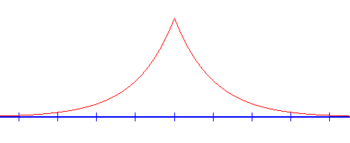График решения волновой функции связанного состояния для потенциала дельта-функции непрерывен всюду, но его производная не определена при x = 0.

В любом одномерном потенциале притяжения будет граница состояние. Чтобы найти его энергию, обратите внимание, что для E < 0, k = i√2m|E|/ħ = iκ is imaginary and the wave functions which were oscillating for positive energies in the calculation above, are now exponentially increasing or decreasing functions of x (see above). Requiring that the wave functions do not diverge at infinity eliminates half of the terms: Ar= B l = 0. Тогда волновая функция

Из граничных условий и условий нормализации следует, что

$\{A\; l\; =\; В\; р\; =\; \kappa ;\; \kappa \; =\; -\; м\; \lambda \; \hslash \; 2;\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{case\}\; A\_\; \{l\}\; =\; B\_\; \{r\}\; =\; \{\backslash \; sqrt\; \{\backslash \; ka\; ppa\}\};\; \backslash \backslash \backslash \; kappa\; =\; -\; \{\backslash \; frac\; \{m\; \backslash \; lambda\}\; \{\backslash \; hbar\; ^\; \{2\}\}\}\; ~;\; \backslash \; end\; \{cases\}\}\}$

откуда следует, что λ должно быть отрицательным, что связанное состояние существует только для ямы, а не для барьера. Преобразование Фурье этой волновой функции является функцией Лоренца.

. Тогда энергия связанного состояния равна

$E\; =\; -\; \hslash \; 2\; \kappa \; 2\; 2\; m\; =\; -\; m\; \lambda \; 2\; 2\; \hslash \; 2.\; \{\backslash \; displaystyle\; E\; =\; -\; \{\backslash \; frac\; \{\backslash \; hbar\; ^\; \{2\}\; \backslash \; kappa\; ^\; \{2\}\}\; \{2m\}\}\; =\; -\; \{\backslash \; frac\; \{m\; \backslash \; lambda\; ^\; \{2\}\}\; \{2\; \backslash \; hbar\; ^\; \{2\}\}\; \}.\}$

Рассеяние (E>0)

Вероятность прохождения (T) и отражения (R) дельта-потенциальной ямы. Энергия E>0 выражается в единицах $м\; \lambda \; 2\; 2\; \hslash \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{m\; \backslash \; lambda\; ^\; \{2\}\}\; \{2\; \backslash \; hbar\; ^\; \{2\}\}\}\; \backslash ,\; \backslash !\}$. Пунктиром: классический результат. Сплошная линия: квантовая механика.

Для положительных энергий частица может свободно двигаться в любом полупространстве: x < 0 or x>0. Он может быть рассеян на потенциале дельта-функции.

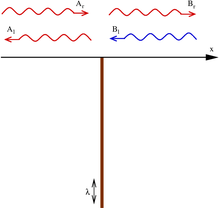
Квантовый случай можно изучить в следующей ситуации: частица, падающая на барьер с левой стороны (A r). Он может быть отражен (A l) или передан (B r). Чтобы найти амплитуды отражения и пропускания при падении слева, мы положим в приведенные выше уравнения A r = 1 (падающая частица), A l = r (отражение), B l = 0 (нет входящей частицы справа) и B r = t (пропускание), и решите для r и t, даже если у нас нет никаких уравнений для t. Результат:

$t\; =\; 1\; 1\; -\; m\; \lambda \; i\; \hslash \; 2\; k\; \{\backslash \; displaystyle\; t\; =\; \{\backslash \; cfrac\; \{1\}\; \{1\; -\; \{\backslash \; cfrac\; \{m\; \backslash \; lambda\}\; \{i\; \backslash \; hbar\; ^\; \{2\}\; k\}\}.\; \}\}\; \backslash ,\; \backslash !\}$

$r\; =\; 1\; я\; \hslash \; 2\; км\; \lambda \; -\; 1\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; cfrac\; \{1\}\; \{\{\backslash \; cfrac\; \{i\; \backslash \; hbar\; ^\; \{2\}\; k\}\; \{m\; \backslash \; lambda\}\; \}\; -1\}\}\; \backslash ,\; \backslash !\}$

Из-за зеркальной симметрии модели амплитуды падения справа такие же, как и слева. В результате существует ненулевая вероятность

$R\; =\; |\; г\; |\; 2\; знак\; равно\; 1\; 1\; +\; \hslash \; 4\; К\; 2\; м\; 2\; \lambda \; 2\; знак\; равно\; 1\; 1\; +\; 2\; \hslash \; 2\; Е\; м\; \lambda \; 2.\; \{\backslash \; displaystyle\; R\; =\; |\; r\; |\; ^\; \{2\}\; =\; \{\backslash \; cfrac\; \{1\}\; \{1\; +\; \{\backslash \; cfrac\; \{\backslash \; hbar\; ^\; \{4\}\; k\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; \backslash \; lambda\; ^\; \{2\}\; \}\}\}\}\; =\; \{\backslash \; cfrac\; \{1\}\; \{1\; +\; \{\backslash \; cfrac\; \{2\; \backslash \; hbar\; ^\; \{2\}\; E\}\; \{m\; \backslash \; lambda\; ^\; \{2\}\}\}\}\}.\; \backslash ,\; \backslash !\}$

для частица для отражения. Это не зависит от знака λ, то есть барьер имеет такую ​​же вероятность отражения частицы, как и яма. Это существенное отличие от классической механики, где вероятность отражения будет равна 1 для барьера (частица просто отскакивает) и 0 для ямы (частица проходит через яму без помех).

Таким образом, вероятность передачи составляет

$T\; =\; |\; т\; |\; 2\; знак\; равно\; 1\; -\; R\; =\; 1\; 1\; +\; м\; 2\; \lambda \; 2\; \hslash \; 4\; К\; 2\; =\; 1\; 1\; +\; м\; \lambda \; 2\; 2\; \hslash \; 2\; E\; \{\backslash \; displaystyle\; T\; =\; |\; t\; |\; ^\; \{2\}\; =\; 1-R\; =\; \{\backslash \; cfrac\; \{1\; \}\; \{1\; +\; \{\backslash \; cfrac\; \{m\; ^\; \{2\}\; \backslash \; lambda\; ^\; \{2\}\}\; \{\backslash \; hbar\; ^\; \{4\}\; k\; ^\; \{2\}\}\}\}\}\; =\; \{\backslash \; cfrac\; \{1\}\; \{1\; +\; \{\backslash \; cfrac\; \{\; m\; \backslash \; lambda\; ^\; \{2\}\}\; \{2\; \backslash \; hbar\; ^\; \{2\}\; E\}\}\}\}\; \backslash ,\; \backslash !\}$.

Замечания и применение

Представленный выше расчет сначала может показаться нереалистичным и вряд ли полезным. Однако она оказалась подходящей моделью для множества реальных систем.

Один из таких примеров касается границ раздела между двумя проводящими материалами. В основной массе материалов движение электронов квазисвободно и может быть описано кинетическим членом в приведенном выше гамильтониане с эффективной массой m. Часто поверхности таких материалов покрыты оксидными слоями или не идеальны по другим причинам. Этот тонкий непроводящий слой можно затем смоделировать с помощью локального дельта-функционального потенциала, как указано выше. Затем электроны могут туннелировать из одного материала в другой, вызывая ток.

Работа сканирующего туннельного микроскопа (СТМ) основана на этом туннельном эффекте. В этом случае барьер возникает из-за наличия воздуха между концом СТМ и нижележащим объектом. Прочность барьера связана с тем, что разделение тем сильнее, чем дальше друг от друга они находятся. Для более общей модели этой ситуации см. Конечный потенциальный барьер (QM). Дельта-функция потенциального барьера является предельным случаем рассматриваемой здесь модели для очень высоких и узких барьеров.

Вышеупомянутая модель одномерна, в то время как пространство вокруг нас трехмерно. Таким образом, фактически следует решать уравнение Шредингера в трех измерениях. С другой стороны, многие системы изменяются только вдоль одного координатного направления и трансляционно инвариантны относительно других. Уравнение Шредингера затем может быть сведено к рассмотренному здесь случаю с помощью анзаца для волновой функции типа $\Psi \; (x,\; y,\; z)\; =\; \psi \; (x)\; \varphi \; (y,\; z)\; \{\backslash \; displaystyle\; \backslash \; Psi\; (\; x,\; y,\; z)\; =\; \backslash \; psi\; (x)\; \backslash \; phi\; (y,\; z)\; \backslash ,\; \backslash !\}$.

В качестве альтернативы можно обобщить дельта-функцию для существования на поверхности некоторой области D (см. Лапласиан индикатора ).

Модель дельта-функции на самом деле является одномерной версией атома водорода согласно методу размерного масштабирования, разработанному группой Дадли Р. Хершбаха Модель дельта-функции становится особенно полезной с двухъямной моделью дельта-функции Дирака, которая представляет одномерную версию иона молекулы водорода, как показано в следующем разделе.

Симметричные и антисимметричные волновые функции для двухъядерной модели дельта-функции Дирака с «межъядерным» расстоянием R = 2.

Двухъядерная дельта-функция Дирака моделирует диатомовые водоросли c молекулы водорода по соответствующему уравнению Шредингера:

$-\; \hslash \; 2\; 2\; md\; 2\; \psi \; dx\; 2\; (x)\; +\; V\; (x)\; \psi \; (x)\; =\; E\; \psi \; (x)\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{\backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; psi\}\; \{dx\; ^\; \{2\}\}\}\; (x)\; +\; V\; (x)\; \backslash \; psi\; (x)\; =\; E\; \backslash \; psi\; (x)\}$

где сейчас потенциал:

$V\; (x)\; =\; -\; q\; [\delta \; (x\; +\; R\; 2)\; +\; \lambda \; \delta \; (x\; -\; R\; 2)]\; \{\backslash \; displaystyle\; V\; (x)\; =\; -\; q\; \backslash \; left\; [\backslash \; delta\; \backslash \; left\; (x\; +\; \{\backslash \; frac\; \{R\}\; \{2\}\}\; \backslash \; right)\; +\; \backslash \; lambda\; \backslash \; delta\; \backslash \; left\; (x\; -\; \{\backslash \; frac\; \{R\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right]\}$

где - это «межъядерное» расстояние с пиками дельта-функции Дирака (отрицательными), расположенными в точке x = ± R / 2 (показано коричневым на диаграмме). Принимая во внимание связь этой модели с ее трехмерным молекулярным аналогом, мы используем атомные единицы и устанавливаем $\hslash \; =\; m\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; hbar\; =\; m\; =\; 1\}$. Здесь - формально настраиваемый параметр. Из случая одной скважины мы можем вывести «анзац » для решения, как:

$\psi \; (x)\; =\; A\; e\; -\; d\; |\; х\; +\; R\; 2\; |\; +\; B\; e\; -\; d\; |\; х\; -\; R\; 2\; |\; \{\backslash \; Displaystyle\; \backslash \; psi\; (х)\; ~\; =\; ~\; Ae\; ^\; \{-\; d\; \backslash \; left\; |\; x\; +\; \{\backslash \; frac\; \{R\}\; \{2\}\}\; \backslash \; right\; |\}\; +\; Be\; ^\; \{-\; d\; \backslash \; left\; |\; x\; -\; \{\backslash \; frac\; \{R\; \}\; \{2\}\}\; \backslash \; right\; |\}\}$

Согласование волновой функции на пиках дельта-функции Дирака дает определитель:

$|\; q\; -\; d\; q\; e\; -\; d\; R\; q\; \lambda \; e\; -\; d\; R\; q\; \lambda \; -\; d\; |\; =\; 0,\; где\; E\; =\; -\; d\; 2\; 2.\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; begin\; \{array\}\; \{cc\}\; q-d\; qe\; ^\; \{-\; dR\}\; \backslash \backslash \; q\; \backslash \; lambda\; e\; ^\; \{-\; dR\}\; q\; \backslash \; lambda\; -d\; \backslash \; end\; \{array\}\}\; \backslash \; right\; |\; =\; 0\; \backslash \; quad\; \{\backslash \; t\_dv\; \{where\}\}\; \backslash \; quad\; E\; =\; -\; \{\backslash \; frac\; \{d\; ^\; \{2\}\}\; \{2\}\}\; ~.\}$

Таким образом, $d\; \{\backslash \; displaystyle\; d\}$определяется псевдоквадратичным уравнением:

$d\; \pm \; (\lambda )\; =\; 1\; 2\; q\; (\lambda \; +\; 1)\; \pm \; 1\; 2\; \{q\; 2\; (1\; +\; \lambda )\; 2\; -\; 4\; \lambda \; q\; 2\; [1\; -\; е\; -\; 2\; d\; \pm \; (\lambda )\; R]\}\; 1/2\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; pm\}\; (\backslash \; lambda)\; ~\; =\; ~\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; q\; (\backslash \; lambda\; +1)\; \backslash \; pm\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; left\; \backslash \; \{q\; ^\; \{2\}\; (1+\; \backslash \; lambda)\; ^\; \{2\}\; -4\; \backslash ,\; \backslash \; lambda\; q\; ^\; \{2\}\; \backslash \; lbrack\; 1-\; e\; ^\; \{-\; 2d\; \_\; \{\backslash \; pm\}\; (\backslash \; lambda)\; R\}]\; \backslash \; right\; \backslash \}\; ^\; \{1/2\}\}$

, который имеет два решения $d\; =\; d\; \pm \; \{\backslash \; displaystyle\; d\; =\; d\; \_\; \{\backslash \; pm\; \}\}$. Для случая равных зарядов (симметричный гомоядерный случай) λ = 1, и псевдоквадратичный сводится к:

$d\; \pm \; =\; q\; [1\; \pm \; e\; -\; d\; \pm \; R]\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; pm\}\; =\; q\; [\; 1\; \backslash \; pm\; e\; ^\; \{-\; d\; \_\; \{\backslash \; pm\}\; R\}]\}$

Случай "+" соответствует волновой функции, симметричной относительно средней точки (показана красным на диаграмме), где A = B и называется Герад. Соответственно, случай «-» - это волновая функция, которая антисимметрична относительно средней точки, где A = –B, называется ungerade (показана зеленым на диаграмме). Они представляют собой приближение двух низших дискретных энергетических состояний трехмерного $H\; 2\; +\; \{\backslash \; displaystyle\; H\_\; \{2\}\; ^\; \{+\}\}$и полезны при его анализе. Аналитические решения для собственных значений энергии для случая симметричных зарядов даются следующим образом:

$d\; \pm \; =\; q\; +\; W\; (\pm \; q\; R\; e\; -\; q\; R)\; /\; R\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; pm\}\; =\; q\; ~\; +\; ~\; W\; (\backslash \; pm\; qRe\; ^\; \{-\; qR\})\; /\; R\}$

где W - стандартная функция W Ламберта. Обратите внимание, что самая низкая энергия соответствует симметричному решению $d\; +\; \{\backslash \; displaystyle\; d\; \_\; \{+\}\}$. В случае неравных зарядов и в этом отношении трехмерной молекулярной проблемы решения даются путем обобщения функции Ламберта W (см. Раздел об обобщении функции Ламберта и ссылки здесь).

Один из наиболее интересных случаев - это когда qR ≤ 1, что приводит к $d\; -\; =\; 0\; \{\backslash \; displaystyle\; d\; \_\; \{-\}\; =\; 0\}$. Таким образом, имеется нетривиальное решение связанного состояния с E = 0. Для этих конкретных параметров проявляется много интересных свойств, одним из которых является необычный эффект, заключающийся в том, что коэффициент передачи равен единице при нулевой энергии.

• Свободная частица
• Частица в коробке
• Конечная потенциальная яма
• W-функция Ламберта
• Частица в кольце
• Частица в сферически-симметричном потенциале
• Квантовый гармонический осциллятор
• Атом водорода или водородоподобный атом
• Кольцевой волновод
• Частица в одномерной решетке (периодический потенциал)
• Молекулярный ион водорода
• Гольштейн –Метод Херринга
• Лапласиан индикатора
• Список квантово-механических систем с аналитическими решениями

1. ^Ланге, Рутгер-Ян (2012), «Теория потенциала, интегралы по траекториям и лапласиан индикатора. ", Journal of High Energy Physics, 2012 (11): 1–49, arXiv : 1302.0864, Bibcode : 2012JHEP... 11..032L, doi : 10.1007 / JHEP11 (2012) 032
2. ^DR Гершбах, И.С. Эйвери и О. Госцински (ред.), Масштабирование размеров в химической физике, Springer, (1992). [1]
3. ^Т.К. Скотт, Дж. Ф. Бэбб, А. Далгарно и Джон Д. Морган III, «Расчет обменных сил: общие результаты и конкретные модели», Дж. Chem. Phys., 99, pp. 2841-2854, (1993). [2]
4. ^У. ван Дейк и К. А. Кирс, "Задержка в простых одномерных системах", Am. J. Phys., 60, стр. 520-527 (1992). [3]

• Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Прентис Холл. С. 68–78. ISBN 978-0-13-111892-8.
• Для трехмерного случая ищите «дельта-потенциал оболочки»; далее см. К. Готфрид (1966), Квантовая механика Том I: Основы, глава III, раздел 15.

• Средства массовой информации, относящиеся к дельта-потенциалу на Wikimedia Commons