W функция Ламберта

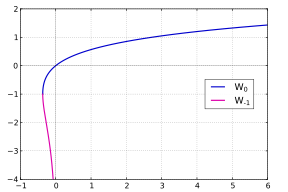
Многозначная «функция» График y = W (x) для действительного x < 6 and y>−4. Верхняя ветвь (синяя) с y ≥ −1 - это график функции W 0 (главная ветвь), нижняя ветвь (пурпурная) с y ≤ −1 - график функции W <103.>−1. Минимальное значение x равно {−1 / e, −1}

. В математике используется функция Ламберта W, также называемая омега-функция или логарифм произведения, является многозначной функцией, а именно ветвями обратной связи функции f (w) = we, где w - любое комплексное число, а e - экспоненциальная функция .

Для каждого целого числа k существует одна ветвь, обозначенная W k (z), которая является комплексной функцией одного комплексного аргумента. W 0 известен как основная ветвь. Эти функции являются следующим своим: если z и w - любые комплексные числа, то

$wew\; =\; z\; \{\backslash \; displaystyle\; we\; ^\; \{w\}\; =\; z\}$

выполняется тогда и только тогда, когда

$w\; =\; W\; k\; (z)\; для\; некоторого\; целого\; k.\; \{\backslash \; displaystyle\; w\; =\; W\_\; \{k\}\; (z)\; \backslash \; \backslash \; \{\backslash \; text\; \{для\; некоторого\; целого\; числа\}\}\; k.\}$

При работе только с действительными числами две ветви W 0 и W −1 достаточно: для действительных чисел x и y уравнение

$yey\; =\; x\; \{\backslash \; displaystyle\; ye\; ^\; \{y\}\; =\; x\}$

может быть решено относительно y, только если x ≥ −1 / e; мы получаем y = W 0 (x), если x ≥ 0, и два значения y = W 0 (x) и y = W −1 ( x), если −1 / e ≤ x < 0.

Отношение Ламберта W не может быть выражено в терминах элементарных функций. Это полезно в комбинаторике, например, при перечислении деревьев. Его можно использовать для решения различных соотношений, включающих экспоненты (например, максимумы распределений Планка, Бозе-Эйнштейна и Ферми-Дирака ), а также решение дифференциальных уравнений с запаздыванием, например y ′ (t) = ay (t - 1). В биохимии и, в частности, в кинетике ферментов, раствор в открытой для анализа форме кинетики времени-изменения кинетики Михаэлиса - Ментен описывается с точки зрения W-функция Ламберта.

Основная ветвь функции Ламберта W на комплексной плоскости. Обратите внимание на отрезок ветви вдоль отрицательной действительной оси, заканчивающийся на -1 / e. На этом рисунке оттенок точки z определяется абсолютным аргументом W (z), а яркость - большим значением W (z).

модуля главной ветви функции Ламберта W, окрашенный в соответствии с arg W (z)

.

• 1 Терминология
• 2 История
• 3 Элементарные свойства, ветви и диапазон
  • 3.1 Обратное
• 4 Исчисление
  • 4.1 Производственное
  • 4.2 Первообразное
• 5 Асимптотические разложения
  • 5.1 Целочисленные и комплексные степени
• 6 Идентичности
• 7 Специальные значения
• 8 Представления
• 9 Другие формулы
  • 9.1 Определенные интегралы
  • 9.2 Неопределенные интегралы
• 10 Приложения
  • 10.1 Решение уравнений
  • 10.2 Вязкие потоки
  • 10.3 Нейровизуализация
  • 10.4 Химическая инженерия
  • 10.5 Материалы
  • 10.6 Пористая среда
  • 10.7 Числа Бернулли и род Тодда
  • 10.8 Статистика
  • 10.9 Точные решения уравнения Шредингера
  • 10.10 Точные решения вакуумных уравнений Эйнштейна
  • 10.11 Резонансы дельты -шель l потенциал
  • 10.12 Термодинамическое равновесие
  • 10.13 Соответствие AdS / CFT
  • 10.14 Эпидемиология
  • 10.15 Определение времени полета снаряда
• 11 Обобщения
• 12 Графики
• 13 Численная оценка
• 14 Программное обеспечение
• 15 См. Также
• 16 Примечания
• 17 Ссылки
• 18 Внешние ссылки

Функция Ламберта W названа в честь Иоганна Генриха Ламберта. Основная ветвь W 0 ена обозначена Wp в Цифровой библиотеке математических функций, а ветвь W -1 здесь обозначена Wm.

Выбранное здесь обозначение (с W 0 и W −1) следует канонической ссылке на функцию Ламберта W Корлессом, Гоннетом, Хэром, Джеффри и Кнут.

Имя «логарифм произведений» можно понимать так: поскольку обратная функция f (w) = e называется логарифмом, это имеет смысл для возврата обратной функции продукта мы как «логарифм продукта». Это связано с омега-константой, которая равна W 0 (1).

Ламберт впервые рассмотрел родственное трансцендентное уравнение Ламберта в 1758 году, что привело к статье Леонарда Эйлера в 1783 году, в котором обсуждался особый случай нас.

Функция, которую рассматривал Ламберт, была

$x\; =\; x\; m\; +\; q.\; \{\backslash \; displaystyle\; x\; =\; x\; ^\; \{m\}\; +\; q.\}$

Эйлер преобразовал это уравнение в форму

$x\; a\; -\; x\; b\; =\; (a\; -\; b)\; c\; x\; a\; +\; b.\; \{\backslash \; displaystyle\; x\; ^\; \{a\}\; -x\; ^\; \{b\}\; =\; (a-b)\; cx\; ^\; \{a\; +\; b\}.\}$

Оба автора получили решение своих уравнений.

После того, как Эйлер решил это уравнение, он рассмотрел случай a = b. Взяв пределы, он вывел уравнение

$ln\; \; x\; =\; c\; x\; a.\; \{\backslash \; displaystyle\; \backslash \; ln\; x\; =\; cx\; ^\; \{a\}.\}$

Затем он положил a = 1 и получил решение сходящегося ряда для полученного уравнения, выразив x через c.

После взятия производных по x и некоторых манипуляций получается стандартный вид функции Ламберта.

В 1993 году, когда было объявлено, что W-функция Ламберта обеспечивает точное решение квантово-механической двухъямной модели дельта-функции Дирака для равных зарядов - фундаментальные проблемы физики - Корлесс и разработчики системы компьютерной алгебры Maple провели поиск в библиотеке и представили, что эта функция является повсеместной по своей природе.

Другой пример, где эта функция встречается, находится в Michaelis - Menten кинетика.

Хотя фольклор знал, что функция Ламберта W не может быть выражена в терминах элементарных (лиувиллевских) функций, первое опубликованное доказательство появилось только в 2008 году.

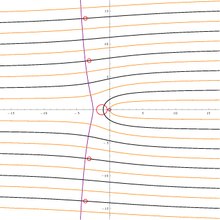
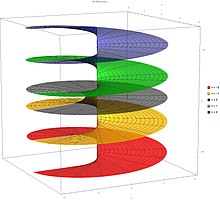
Диапазон функции W с отображением всех ветвей. Черные кривые (включая действительную ось) образуют изображение обратной оси, оранжевые кривые - изображение мнимой оси. Фиолетовая кривая - это изображение небольшого круга вокруг точки z = 0; красные кривые - это изображение маленького круга вокруг точки z = −1 / e. График мнимой части W [n, x + iy] для ветвей n = -2, -1,0,1, 2. График аналогичен графику многозначной функции комплексного логарифма , за исключением того, что расстояние между листами не является постоянным, а соединение основного листа отличается

Существует счетное множество ветвей функции W, обозначенных на W k (z) для целого k; W 0 (z) - главная или основная ветвь. W 0 (z) определен для всех комплексных чисел z, тогда как W k (z) с k ≠ 0 определен для всех ненулевых z. Имеем W 0 (0) = 0 и limz → 0 W k (z) = −∞ для всех k ≠ 0.

Точка ветвления для главной ветвь находится в точке z = −1 / e, с разрезом ветви, который продолжается до −∞ вдоль отрицательной действительной оси. Этот разрез ветвей отделяет главную ветвь от двух ветвей W -1 и W 1. Во всех ветвях W k с k ≠ 0 имеется точка ветвления в точке z = 0 и ветвь, разрезанная вдоль всей отрицательной действительной оси.

Функции W k (z), k ∈ Z все инъективны и их диапазоны не пересекаются. Образом всей многозначной функции W является комплексная плоскость. Изображение действительной оси представляет собой объединение действительной и квадратисы Гиппия, параметрической кривой w = −t cot t + it.

Обратный

Области комплексной плоскости, для которых $W\; (n,\; z\; e\; z)\; =\; z\; \{\backslash \; displaystyle\; W\; (n,\; ze\; ^\; \{z\})\; =\; z\}$. Более темные границы того же цвета включаются в более светлую область того же цвета. Точка в {-1,0} входит как в область $n\; =\; -\; 1\; \{\backslash \; displaystyle\; n\; =\; -1\}$(синий), так и в область $n\; =\; 0\; \{\backslash \; displaystyle\; n\; =\; 0\}$(серая) область. Горизонтальные линии сетки кратны π.

График вышеупомянутой области в плоскости плоскости, где простая обратная '$W\; (n,\; zez)\; =\; z\; \{\backslash \; displaystyle\; W\; (n,\; ze\; ^\; \{z\})\; =\; z\}$верно. f = ze означает, что существует n такое, что $z\; =\; W\; (n,\; f)\; =\; W\; (n,\; zez)\; \{\backslash \; displaystyle\; z\; =\; W\; (n,\; f)\; =\; W\; (n,\; ze\; ^\; \{z\})))\}$, где n будет зависеть от значений z. Значение целого числа n резко изменится, когда ze станет означать на отрезке ветви $W\; (n,\; zez)\; \{\backslash \; displaystyle\; W\; (n,\; ze\; ^\; \{z\})\}$, что будет означать, что ze ≤ 0, за исключением $n\; =\; 0\; \{\backslash \; displaystyle\; n\; =\; 0\}$, где ze ≤ -1 / e.

Определите $z\; =\; x\; +\; i\; y\; \{\backslash \; displaystyle\; z\; =\; x\; +\; iy\}$, где x и y действительны. Выражая e в полярных координатах, видно, что:

$zez\; =\; (x\; +\; iy)\; ex\; (cos\; \; (y)\; +\; i\; sin\; \; (y))\; =\; ex\; (x\; cos\; \; (y)\; -\; y\; sin\; \; (y))\; +\; iex\; (x\; грех\; \; (y)\; +\; y\; соз\; \; (y))\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; ze\; ^\; \{z\}\; =\; (x\; +\; iy)\; e\; ^\; \{x\}\; (\backslash \; cos\; (y)\; +\; i\; \backslash \; sin\; (y))\; \backslash \backslash \; =\; e\; ^\; \{x\}\; (x\; \backslash \; cos\; (y)\; -y\; \backslash \; sin\; (y))\; +\; ie\; ^\; \{x\}\; (x\; \backslash \; sin\; (y)\; +\; y\; \backslash \; cos\; (y))\; \backslash \backslash \backslash \; конец\; \{выровнен\}\}\}$

Для $n\; \ne \; 0\; \{\backslash \; displaystyle\; n\; \backslash \; neq\; 0\}$, отрезок ветви для $W\; [n,\; zez]\; \{\backslash \; displaystyle\; W\; [n,\; ze\; ^\; \{z\}]\}$будет неположительной действительной осью, так что:

$x\; sin\; \; (y)\; +\; y\; cos\; \; (y)\; =\; 0\; \Rightarrow \; x\; =\; -\; y\; /\; загар\; \; (y)\; \{\backslash \; displaystyle\; x\; \backslash \; sin\; (y)\; +\; y\; \backslash \; cos\; (y)\; =\; 0\; \backslash \; Rightarrow\; x\; =\; -y\; /\; \backslash \; tan\; (y)\}$

и

$(Икс\; соз\; \; (\; Y)\; -\; Y\; грех\; \; (Y))\; ex\; \le \; 0\; \{\backslash \; Displaystyle\; (x\; \backslash \; cos\; (y)\; -y\; \backslash \; sin\; (y))\; e\; ^\; \{x\}\; \backslash \; Leq\; 0\}$

Для $n\; =\; 0\; \{\backslash \; displaystyle\; n\; =\; 0\}$, отрезок ветви для $W\; [n,\; zez]\; \{\backslash \; displaystyle\; W\; [n,\; ze\; ^\; \{z\}]\}$будет действительной осью с , так что неравенство будет имет ь вид:

$(x\; соз\; \; (y)\; -\; y\; sin\; \; (y))\; ex\; \le \; -\; 1\; /\; e\; \{\backslash \; dis\; playstyle\; (x\; \backslash \; cos\; (y)\; -y\; \backslash \; sin\; (y))\; e\; ^\; \{x\; \}\; \backslash \; leq\; -1\; /\; e\}$

Внутри границ, ограниченных указанным выше, не будет прерывистых изменений в $W\; (n,\; zez)\; \{\backslash \; displaystyle\; W\; (n,\; ze\; ^\; \{z\})\}$, и эти области будут указывать, где функция W просто обратима: т.е. $W\; (n,\; zez)\; =\; z\; \{\backslash \; displaystyle\; W\; (n,\; ze\; ^\; \{z\})\; =\; z\}$.

Производная

С помощью неявного дифференцирования можно показать, что все ветви W удовлетворяет дифференциальному уравнению

$z\; (1\; +\; W)\; d\; W\; dz\; =\; W\; для\; z\; -\; 1\; e.\; \{\backslash \; displaystyle\; z\; (1\; +\; W)\; \{\backslash \; frac\; \{dW\}\; \{dz\}\}\; =\; W\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; z\; \backslash \; neq\; -\; \{\backslash \; frac\; \{1\}\; \{e\}\}.\}$

( W не дифференцируемо для z = −1 / e.) Как следствие, мы получаем формулу для производной W:

$d\; W\; dz\; =\; W\; (z)\; z\; (1\; +\; W\; (z))\; для\; z\; \notin \; \{0,\; -\; 1\; e\}.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dW\}\; \{dz\}\}\; =\; \{\backslash \; frac\; \{W\; (z)\}\; \{z\; (1\; +\; W\; (z))\}\}\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; z\; \backslash \; not\; \backslash \; in\; \backslash \; left\; \backslash \; \{0,\; -\; \{\backslash \; frac\; \{1\}\; \{e\}\}\; \backslash \; right\; \backslash \}.\}$

Используя тождество e = z / W (z), мы получаем эквивалентную формулу:

$d\; W\; dz\; =\; 1\; z\; +\; e\; W\; (z)\; для\; z\; \ne \; -\; 1\; e.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dW\}\; \{dz\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{z\; +\; e\; ^\; \{W\; (z)\}\}\}\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; z\; \backslash \; neq\; -\; \{\backslash \; frac\; \{\; 1\}\; \{e\}\}.\}$

В начале координат мы имеем

$W\; 0\; \prime \; (0)\; =\; 1.\; \{\backslash \; displaystyle\; W\; \text{'}\_\; \{0\}\; (0)\; =\; 1.\}$

Первообразная

Функция W (x) и многие выражения, включающие W (x), могут быть интегрированы с помощью подстановки w = W (x), т.е. x = мы:

$\int \; W\; (x)\; dx\; =\; x\; W\; (x)\; -\; x\; +\; e\; W\; (x)\; +\; C\; =\; x\; (W\; (x)\; -\; 1\; +\; 1\; W\; (x))\; +\; C.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; W\; (x)\; \backslash ,\; dx\; =\; xW\; (x)\; -x\; +\; e\; ^\; \{W\; (x)\}\; +\; C\; \backslash \backslash \; =\; x\; \backslash \; left\; (W\; (x)\; -1\; +\; \{\backslash \; frac\; \{1\}\; \{W\; (x)\}\}\; \backslash \; right)\; +\; C.\; \backslash \; end\; \{align\}\}\}$

(Последнее уравнение часто встречается в литературе, но не выполняется при x = 0). Одним из следствий этого (используя тот факт, что W 0 (e) = 1) является тождеством

$\int \; 0\; e\; W\; 0\; (x)\; dx\; =\; e\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\; 0\}\; ^\; \{e\}\; W\_\; \{0\}\; (x)\; \backslash ,\; dx\; =\; e-1.\}$

Ряд Тейлора W 0 около 0 можно найти с помощью теоремы об обращении Лагранжа и определяется как

$W\; 0\; (x)\; =\; \sum \; n\; =\; 1\; \infty \; (-\; n)\; n\; -\; 1\; n!\; Икс\; N\; знак\; равно\; Икс\; -\; Икс\; 2\; +\; 3\; 2\; Икс\; 3-8\; 3\; Икс\; 4\; +\; 125\; 24\; Х\; 5\; -\; \cdots .\; \{\backslash \; displaystyle\; W\_\; \{0\}\; (x)\; =\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-n)\; ^\; \{n-1\}\}\; \{n!\}\}\; x\; ^\; \{n\}\; =\; xx\; ^\; \{2\}\; +\; \{\backslash \; tfrac\; \{3\}\; \{2\}\}\; x\; ^\; \{3\}\; -\; \{\backslash \; tfrac\; \{8\}\; \{3\}\}\; x\; ^\; \{4\}\; +\; \{\backslash \; tfrac\; \{125\}\; \{24\}\}\; x\; ^\; \{5\}\; -\; \backslash \; cdots.\}$

Радиус сходимости равенство 1 / e, что можно увидеть с помощью теста отношения . Функция, определяемая этим рядом, может быть расширена до голоморфной функции , определенные на всех комплексных числах с отрезком ветви вдоль интервала (−∞, −1 / e] ; эта голоморфная функция определяет главная ветвь функции Ламберта W.

Для больших значений x W 0 асимптотичен

$W\; 0\; (x)\; =\; L\; 1\; -\; L\; 2\; +\; L\; 2\; L\; 1\; +\; L\; 2\; (-\; 2\; +\; L\; 2)\; 2\; L\; 1\; 2\; +\; L\; 2\; (6-9\; L\; 2\; +\; 2\; L\; 2\; 2)\; 6\; L\; 1\; 3\; +\; L\; 2\; (-\; 12\; +\; 36\; L\; 2\; -\; 22\; L\; 2\; 2\; +\; 3\; L\; 2\; 3)\; 12\; L\; 1\; 4\; +\; \cdots \; =\; L\; 1\; -\; L\; 2\; +\; \sum \; l\; =\; 0\; \infty \; \sum \; m\; =\; 1\; \infty \; (-\; 1)\; l\; [l\; +\; ml\; +\; 1]\; ì!\; L\; 1\; -\; l\; -\; м\; L\; 2\; м,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; W\_\; \{0\}\; (x)\; =\; L\_\; \{1\}\; -L\_\; \{2\}\; +\; \{\backslash \; frac\; \{L\_\; \{2\}\}\; \{L\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{L\_\; \{2\}\; \backslash \; left\; (-2\; +\; L\_\; \{2\}\; \backslash \; right)\}\; \{2L\_\; \{1\}\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{L\_\; \{2\}\; \backslash \; left\; (6-9L\_\; \{\; 2\}\; +\; 2L\_\; \{2\}\; ^\; \{2\}\; \backslash \; right)\}\; \{6L\_\; \{1\}\; ^\; \{3\}\}\}\; +\; \{\backslash \; frac\; \{L\_\; \{2\}\; \backslash \; left\; (-12+\; 36L\_\; \{2\}\; -22L\_\; \{2\}\; ^\; \{2\}\; +\; 3L\_\; \{2\}\; ^\; \{3\}\; \backslash \; right)\}\; \{12L\_\; \{1\}\; ^\; \{4\}\}\}\; +\; \backslash \; cdots\; \backslash \backslash \; [5pt]\; =\; L\_\; \{1\}\; -L\_\; \{2\}\; +\; \backslash \; sum\; \_\; \{l\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; sum\; \_\; \{m\; =\; 1\}\; ^\; \{\backslash \; inft\; y\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{l\}\; \backslash \; left\; [\{\backslash \; begin\; \{smallmatrix\}\; l\; +\; m\; \backslash \backslash \; l\; +\; 1\; \backslash \; end\; \{smallmatrix\}\}\; \backslash \; right]\}\; \{m!\}\}\; L\_\; \{1\}\; ^\; \{-\; lm\}\; L\_\; \{2\}\; ^\; \{m\},\; \backslash \; end\; \{align\}\}\}$

где L 1 = ln x, L 2 = ln ln x, и [. l + 1 ]- неотрицательное число Стирлинга первого рода. Сохраняя только первые два членских разложения,

$W\; 0\; (x)\; =\; ln\; \; x\; -\; ln\; \; ln\; \; x\; +\; o\; (1).\; \{\backslash \; displaystyle\; W\_\; \{0\}\; (x)\; =\; \backslash \; ln\; x-\; \backslash \; ln\; \backslash \; ln\; x\; +\; o\; (1).\}$

Другая действительная ветвь, W −1, определенная в интервале [−1 / e, 0), имеет приближение того же вида, когда x стремится к нулю, в этом случае L 1 = ln (−x) и L 2 = ln (−ln ( −x)).

Показано, что имеет место следующая оценка (верхняя оценка только для x ≥ e):

$ln\; \; x\; -\; ln\; \; ln\; \; x\; +\; ln\; \; ln\; \; Икс\; 2\; ln\; \; x\; \le \; W\; 0\; (x)\; \le \; ln\; \; x\; -\; ln\; \; ln\; \; x\; +\; ee\; -\; 1\; ln\; \; ln\; \; x\; ln\; \; x.\; \{\backslash \; Displaystyle\; \backslash \; пер\; х-\; \backslash \; пер\; \backslash \; пер\; Икс\; +\; \{\backslash \; гидроразрыва\; \{\backslash \; пер\; \backslash \; пер\; х\}\; \{2\; \backslash \; пер\; х\}\}\; \backslash \; leq\; W\_\; \{0\}\; (х)\; \backslash \; Leq\; \backslash \; пер\; х-\; \backslash \; пер\; \backslash \; пер\; х\; +\; \{\backslash \; frac\; \{e\}\; \{e-1\}\}\; \{\backslash \; frac\; \{\backslash \; ln\; \backslash \; ln\; x\}\; \{\backslash \; ln\; x\}\}.\}$

В 2013 году было доказано, что ветвь W −1 может быть ограниченным следующим образом:

Целочисленные и комплексные степени

Целочисленные вложения степени W 0 Разные степени W 0 ряд Тейлора (или Лорана ) в нуле:

$W\; 0\; (x)\; 2\; =\; \sum \; n\; =\; 2\; \infty \; -\; 2\; (-\; n)\; n\; -\; 3\; (n\; -\; 2)!\; xn\; знак\; равно\; x\; 2\; -\; 2\; x\; 3\; +\; 4\; x\; 4\; -\; 25\; 3\; x\; 5\; +\; 18\; x\; 6\; -\; \cdots .\; \{\backslash \; displaystyle\; W\_\; \{0\}\; (x)\; ^\; \{2\}\; =\; \backslash \; sum\; \_\; \{n\; =\; 2\}\; ^\; \{\backslash \; infty\; \}\; \{\backslash \; frac\; \{-2\; \backslash \; left\; (-n\; \backslash \; right)\; ^\; \{n-3\}\}\; \{(n-2)!\}\}\; x\; ^\; \{n\}\; =\; x\; ^\; \{2\}\; -2x\; ^\; \{3\}\; +\; 4x\; ^\; \{4\}\; -\; \{\backslash \; tfrac\; \{25\}\; \{3\}\}\; x\; ^\; \{5\}\; +\; 18x\; ^\; \{6\}\; -\; \backslash \; cdots.\}$

В общем, для r ∈ ℤ Формула обращения Лагранжа дает

$W\; 0\; (x)\; r\; =\; \sum \; n\; =\; r\; \infty \; -\; r\; (-\; n)\; n\; -\; r\; -\; 1\; (n\; -\; r)!\; Xn,\; \{\backslash \; displaystyle\; W\_\; \{0\}\; (x)\; ^\; \{r\}\; =\; \backslash \; sum\; \_\; \{n\; =\; r\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{-r\; \backslash \; left\; (-n\; \backslash \; right)\; ^\; \{nr-1\}\}\; \{(nr)!\}\}\; x\; ^\; \{\; n\},\}$

который, в общем, является рядо м Лорана порядка r. Эквивалентно, последний может быть записан в форме Taylor ex расширение степеней W 0 (x) / x:

$(W\; 0\; (x)\; x)\; r\; =\; e\; -\; r\; W\; 0\; (x)\; =\; \sum \; n\; =\; 0\; \infty \; г\; (п\; +\; г)\; п\; -\; 1\; п!\; (-\; х)\; n,\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{W\_\; \{0\}\; (x)\}\; \{x\}\}\; \backslash \; right)\; ^\; \{r\}\; =\; e\; ^\; \{-\; rW\_\; \{0\}\; (x)\}\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{r\; \backslash \; left\; (n\; +\; r\; \backslash \; right)\; ^\; \{n-1\}\}\; \{n!\}\}\; \backslash \; left\; (-x\; \backslash \; right)\; ^\; \{n\},\}$

это происходит для любого r ∈ ℂ и | х | < 1/e.

График W j (x e), где синий - для j = 0, а красный - для j = -1. Диагональная линия представляет интервалы, где W j (xe) = x

Из определения следует несколько тождеств:

$W\; 0\; (xex)\; =\; x\; для\; x\; \ge \; -\; 1,\; W\; -\; 1\; (xex)\; =\; x\; для\; x\; \le \; -\; 1.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; W\_\; \{0\}\; (xe\; ^\; \{x\})\; =\; x\; \{\backslash \; text\; \{for\}\}\; x\; \backslash \; geq\; -1,\; \backslash \backslash \; W\_\; \{\; -1\}\; (xe\; ^\; \{x\})\; =\; x\; \{\backslash \; text\; \{for\}\}\; x\; \backslash \; leq\; -1.\; \backslash \; End\; \{align\}\}\}$

Обратите внимание, что, поскольку f (x) = xe не injective, не всегда верно, что W (f (x)) = x, как и в случае с обратными тригонометрическими функциями . Для фиксированного x < 0 and x ≠ −1, the equation xe = ye has two solutions in y, one of which is of course y = x. Then, for i = 0 and x < −1, as well as for i = −1 and x ∈ (−1, 0), y = Wi (xe) - другое решение.

Некоторые другие тождества:

$W\; (x)\; \cdot \; e\; W\; (x)\; =\; x,\; следовательно:\; e\; W\; (x)\; =\; x\; W\; (x),\; e\; -\; W\; (x)\; =\; W\; (x)\; x,\; en\; W\; (x)\; =\; (x\; W\; (x))\; n.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; W\; (x)\; \backslash \; cdot\; e\; ^\; \{W\; (x)\}\; =\; x,\; \backslash \; quad\; \{\backslash \; text\; \{,\; следовательно:\}\}\; \backslash \backslash \; [5pt]\; e\; ^\; \{W\; (x)\}\; =\; \{\backslash \; frac\; \{x\}\; \{W\; (x)\}\},\; \backslash \; qquad\; e\; ^\; \{-\; W\; (x)\}\; =\; \{\backslash \; frac\; \{W\; (x)\}\; \{x\}\},\; \backslash \; qquad\; e\; ^\; \{nW\; (\; x)\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{W\; (x)\}\}\; \backslash \; right)\; ^\; \{n\}.\; \backslash \; end\; \{align\}\}\}$

$ln\; \; W\; 0\; (x)\; =\; ln\; \; x\; -\; W\; 0\; (x)\; для\; x>0.\; \{\backslash \; displaystyle\; \backslash \; ln\; W\_\; \{0\}\; (x)\; =\; \backslash \; ln\; x-W\_\; \{0\}\; (x)\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; x>0.\}$

$W\; 0\; (x\; ln\; \; x)\; =\; пер\; \; Икс\; и\; е\; W\; 0\; (Икс\; пер\; \; Икс)\; =\; Икс\; для\; Икс\; \ge \; 1\; е.\; \{\backslash \; Displaystyle\; W\_\; \{0\}\; \backslash \; left\; (x\; \backslash \; ln\; x\; \backslash \; right)\; =\; \backslash \; ln\; x\; \backslash \; quad\; \{\backslash \; text\; \{и\}\; \}\; \backslash \; quad\; e\; ^\; \{W\_\; \{0\}\; \backslash \; left\; (x\; \backslash \; ln\; x\; \backslash \; right)\}\; =\; x\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; x\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{e\}\}.\}$

$W\; -\; 1\; (Икс\; пер\; \; Икс)\; знак\; равно\; пер\; \; Икс\; и\; е\; W\; -\; 1\; (Икс\; пер\; \; Икс)\; =\; Икс\; для\; Икс\; \le \; 1\; е.\; \{\backslash \; Displaystyle\; W\; \_\; \{-\; 1\}\; \backslash \; влево\; (х\; \backslash \; пер\; х\; \backslash \; вправо)\; =\; \backslash \; ln\; x\; \backslash \; quad\; \{\backslash \; text\; \{and\}\}\; \backslash \; quad\; e\; ^\; \{W\; \_\; \{-\; 1\}\; \backslash \; left\; (x\; \backslash \; ln\; x\; \backslash \; right)\}\; =\; x\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; x\; \backslash \; leq\; \{\backslash \; frac\; \{1\}\; \{e\}\}.\}$

$W\; (x)\; =\; ln\; \; x\; W\; (x)\; для\; x\; \ge \; -\; 1\; e,\; W\; (nxn\; W\; (x)\; n\; -\; 1)\; =\; n\; W\; (\; x)\; для\; n,\; x>0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; W\; (x)\; =\; \backslash \; ln\; \{\backslash \; frac\; \{x\}\; \{W\; (x)\}\}\; \{\backslash \; text\; \{for\}\}\; x\; \backslash \; geq\; -\; \{\backslash \; frac\; \{1\}\; \{e\}\},\; \backslash \backslash \; [5pt]\; W\; \backslash \; left\; (\; \{\backslash \; frac\; \{nx\; ^\; \{n\}\}\; \{W\; \backslash \; left\; (x\; \backslash \; right)\; ^\; \{n-1\}\}\}\; \backslash \; right)\; =\; nW\; (x)\; \{\backslash \; text\; \{for\}\}\; n,\; x>0\; \backslash \; end\; \{align\}\}\}$

(который может быть расширен на другие n и x, если правильная ветка выбрано).

$W\; (x)\; +\; W\; (y)\; =\; W\; (xy\; (1\; W\; (x)\; +\; 1\; W\; (y)))\; для\; x,\; y>0.\; \{\backslash \; Displaystyle\; W\; (x)\; +\; W\; (y)\; =\; W\; \backslash \; left\; (xy\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{W\; (x)\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{W\; (y)\}\}\; \backslash \; справа)))\; \backslash \; right)\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; x,\; y>0.\}$

Подставляя −ln x в определение:

С повторяющейся экспонентой Эйлера h (x):

$h\; (x)\; =\; e\; -\; W\; (-\; ln\; \; x)\; =\; W\; (-\; пер\; \; Икс)\; -\; пер\; \; Икс\; для\; Икс\; \ne \; 1.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; h\; (x)\; =\; e\; ^\; \{-\; W\; (-\; \backslash \; ln\; x)\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\; W\; (-\; \backslash \; ln\; x)\}\; \{-\; \backslash \; ln\; x\}\}\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; x\; \backslash \; ne\; q\; 1.\; \backslash \; end\; \{align\}\}\}$

Для любого ненулевого алгебраическое число x, W (x) трансцендентным номером. В самом деле, если W (x) равно нулю, то x также должно быть равен нулю, а если W (x) ненулевой и алгебраический, то по теореме Линдемана - Вейерштрасса, e должен быть трансцендентным, что означает, что x = W (x) также должен быть трансцендентным.

Следующие специальные значения главной ветви:

$W\; (-\; \pi \; 2)\; =\; i\; \pi \; 2.\; \{\backslash \; displaystyle\; W\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; =\; \{\; \backslash \; frac\; \{i\; \backslash \; pi\}\; \{2\}\}.\}$

$W\; (-\; 1\; e)\; =\; -\; 1.\; \{\backslash \; displaystyle\; W\; \backslash \; left\; (-\; \{\backslash \; frac\; \{1\}\; \{e\}\}\; \backslash \; right)\; =\; -\; 1.\}$

$W\; (-\; ln\; \; aa)\; =\; -\; ln\; \; a\; (1\; e\; \le \; a\; \le \; e).\; \{\backslash \; displaystyle\; W\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; ln\; a\}\; \{a\}\}\; \backslash \; right)\; =\; -\; \backslash \; ln\; a\; \backslash \; quad\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{e\}\}\; \backslash \; leq\; a\; \backslash \; leq\; e\; \backslash \; справа).\}$

$W\; (2\; пер\; \; 2)\; =\; пер\; \; 2.\; \{\backslash \; displaystyle\; W\; \backslash \; left\; (2\; \backslash \; ln\; 2\; \backslash \; right)\; =\; \backslash \; ln\; 2.\}$

$W\; (0)\; =\; 0.\; \{\; \backslash \; Displaystyle\; W\; (0)\; =\; 0.\}$

$W\; (1)\; =\; \Omega \; =\; (\int \; -\; \infty \; \infty \; dt\; (et\; -\; t)\; 2\; +\; \pi \; 2)\; -\; 1-1\; \approx \; 0,56714329\dots \; \{\backslash \; displaystyle\; W\; (\; 1)\; =\; \backslash \; Omega\; =\; \backslash \; left\; (\backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{dt\}\; \{\backslash \; left\; (e\; ^\; \{t\}\; -t\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; pi\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{-\; 1\}\; -1\; \backslash \; приблизительно\; 0,56714329\; \backslash \; ldots\}$(постоянная омега ).

$W\; (1)\; =\; e\; -\; W\; (1)\; =\; пер\; \; (1\; W\; (1))\; знак\; равно\; -\; пер\; \; W\; (1).\; \{\backslash \; Displaystyle\; W\; (1)\; =\; e\; ^\; \{-\; W\; (1)\}\; =\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{W\; (1)\}\}\; \backslash \; right)\; =\; -\; \backslash \; ln\; W\; (1).\}$

$W\; (e)\; =\; 1.\; \{\backslash \; displaystyle\; W\; (e)\; =\; 1.\}$

$W\; (e\; 1\; +\; e)\; Знак\; равно\; е.\; \{\backslash \; Displaystyle\; W\; \backslash \; left\; (e\; ^\; \{1\; +\; e\}\; \backslash \; right)\; =\; e.\}$

$W\; (-\; 1)\; \approx \; -\; 0,31813\; +\; 1,33723\; i.\; \{\backslash \; Displaystyle\; W\; (-\; 1)\; \backslash \; приблизительно\; -0,31813\; +\; 1,33723i.\}$

Основныевь функц ии Лам берта может быть представлен интегралом благодаря Пуассону:

В более широкой области −1 / e ≤ x ≤ e значительно более простое представление находится с помощью Mező:

$W\; (x)\; =\; 1\; \pi \; Re\; \; \int \; 0\; \pi \; ln\; \; (eeit\; -\; xe\; -\; iteeit\; -\; xeit)\; dt.\; \{\backslash \; displaystyle\; W\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; operatorname\; \{Re\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{e\; ^\; \{e\; ^\; \{\; it\}\}\; -\; xe\; ^\; \{-\; it\}\}\; \{e\; ^\; \{e\; ^\; \{it\}\}\; -\; xe\; ^\; \{it\}\}\}\; \backslash \; right)\; \backslash ,\; dt.\}$

Следующая непрерывная дробь представление также справедливо для главной ветви:

$W\; (x)\; =\; x\; 1\; +\; x\; 1\; +\; x\; 2\; +\; 5\; x\; 3\; +\; 17\; x\; 10\; +\; 133\; x\; 17\; +\; 1927\; x\; 190\; +\; 13582711\; x\; 94423\; +\; \ddots .\; \{\backslash \; Displaystyle\; W\; (x)\; =\; \{\backslash \; cfrac\; \{x\}\; \{1\; +\; \{\backslash \; cfrac\; \{x\}\; \{1\; +\; \{\backslash \; cfrac\; \{x\}\; \{2\; +\; \{\backslash \; cfrac\; \{5x\}\; \{3\; +\; \{\backslash \; cfrac\; \{17x\})))\; \{10\; +\; \{\backslash \; cfrac\; \{133x\}\; \{17\; +\; \{\backslash \; cfrac\; \{1927x\}\; \{190\; +\; \{\backslash \; cfrac\; \{13582711x\}\; \{94423+\; \backslash \; ddots\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}.\; \}$

Также, если | W (z) | < 1:

$W\; (x)\; =\; x\; exp\; \; x\; exp\; \; x\; \ddots .\; \{\backslash \; displaystyle\; W\; (x)\; =\; \{\backslash \; cfrac\; \{x\}\; \{\backslash \; exp\; \{\backslash \; cfrac\; \{x\}\; \{\backslash \; exp\; \{\backslash \; cfrac\; \{x\}\; \{\backslash \; ddots\}\}\}\}\}\}.\}$

В свою очередь, если | W (z) |>е, то

$W\; (x)\; =\; ln\; \; x\; ln\; \; x\; ln\; \; x\; \ddots .\; \{\backslash \; displaystyle\; W\; (x)\; =\; \backslash \; ln\; \{\backslash \; cfrac\; \{x\}\; \{\backslash \; ln\; \{\backslash \; cfrac\; \{x\}\; \{\backslash \; ln\; \{\backslash \; cfrac\; \{x\}\; \{\backslash \; ddots\}\}\}\}\}\}.\}$

.

Определенные интегралы

Существует несколько полезных формул определенного интеграла, включающих основные ветвь функции W, в том числе следующие:

$\int \; 0\; \pi \; W\; (2\; cot\; 2\; \; x)\; sec\; 2\; \; xdx\; =\; 4\; \pi .\; \int \; 0\; \infty \; W\; (Икс)\; Икс\; Икс\; d\; Икс\; знак\; равно\; 2\; 2\; \pi .\; \int \; 0\; \infty \; W\; (1\; x\; 2)\; d\; x\; =\; 2\; \pi .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; W\; \backslash \; left\; (2\; \backslash \; cot\; ^\; \{2\}\; x\; \backslash \; right)\; \backslash \; sec\; ^\; \{2\}\; x\; \backslash ,\; dx\; =\; 4\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}.\; \backslash \backslash \; [5pt]\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{W\; (x)\}\; \{x\; \{\backslash \; sqrt\; \{x\}\}\}\}\; \backslash ,\; dx\; =\; 2\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\; \}.\; \backslash \backslash \; [5pt]\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; W\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{x\; ^\; \{2\}\}\}\; \backslash \; right)\; \backslash ,\; dx\; =\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\; \}.\; \backslash \; end\; \{align\}\}\}$

Первую идентичность можно найти, записав интеграл Гаусса в полярных координат.

Вторая идентичность можно получить, сделав замену u = W (x), которая дает

$х\; =\; ueu,\; dxdu\; =\; (u\; +\; 1)\; eu.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; =\; ue\; ^\; \{u\},\; \backslash \backslash \; [5pt]\; \{\backslash \; frac\; \{dx\}\; \{du\}\}\; =\; (u\; +\; 1)\; e\; ^\; \{u\}.\; \backslash \; end\; \{выравнивается\}\}\}$

Таким образом,

$∫ 0 ∞ W (x) xxdx = ∫ 0 ∞ uueuueu (u + 1) eudu = ∫ 0 ∞ u + 1 ueudu = ∫ 0 ∞ u + 1 u 1 eudu = ∫ 0 ∞ u 1 2 e - u 2 du + ∫ 0 ∞ u - 1 2 e - u 2 du = 2 ∫ 0 ∞ (2 w) 1 2 e - wdw + 2 ∫ 0 ∞ (2 w) - 1 2 e - wdw (u = 2 w) = 2 2 ∫ 0 ∞ w 1 2 e - wdw + 2 ∫ 0 ∞ w - 1 2 e - wdw = 2 2 ⋅ Γ (3 2) + 2 ⋅ Γ (1 2) = 2 2 (1 2 π) + 2 (π) = 2 2 π. {\ displaystyle {\ begin {align} \ int _ {0} ^ {\ infty} {\ frac {W (x)} {x {\ sqrt {x}}}} \, dx = \ int _ {0 } ^ {\ infty} {\ frac {u} {ue ^ {u} {\ sqrt {ue ^ {u}}}}} (u + 1) e ^ {u} \, du \\ [5pt] = \ int _ {0} ^ {\ infty} {\ frac {u + 1} {\ sqrt {ue ^ {u}}}} du \\ [5pt] = \ int _ {0} ^ {\ infty } {\ frac {u + 1} {\ sqrt {u}}} {\ frac {1} {\ sqrt {e ^ {u}}}} du \\ [5pt] = \ int _ {0} ^ {\ infty} u ^ {\ tfrac {1} {2}} e ^ {- {\ frac {u} {2}}} du + \ int _ {0} ^ {\ infty} u ^ {- {\ tfrac {1} {2}}} e ^ {- {\ frac {u} {2}}} du \\ [5pt] = 2 \ int _ {0} ^ {\ infty} (2w) ^ {\ tfrac {1} {2}} e ^ {- w} \, dw + 2 \ int _ {0} ^ {\ infty} (2w) ^ {- {\ tfrac {1} {2}}} e ^ { - w} \, dw \ quad (u = 2w) \\ [5pt] = 2 {\ sqrt {2}} \ int _ {0} ^ {\ infty} w ^ {\ tfrac {1} {2 }} e ^ {- w} \, dw + {\ sqrt {2}} \ int _ {0} ^ {\ infty} w ^ {- {\ tfrac {1} {2}}} e ^ {- w } \, dw \\ [5pt] = 2 {\ sqrt {2}} \ cdot \ Gamma \ left ({\ tfrac {3} {2}} \ right) + {\ sqrt {2}} \ cdot \ Гамма \ влево ({\ tfrac {1} {2}} \ right) \\ [5pt] = 2 {\ sqrt {2}} \ left ({\ tfrac {1} {2}} {\ sqrt {\ pi}} \ right) + {\ sqrt {2}} \ left ({\ sqrt {\ pi}} \ right) \\ [5pt] = 2 {\ sqrt {2 \ pi}}. \ end {align}}}$

Третья идентичность может быть получена из второго, если замена u = x, и первое также может быть получено из третьего пути замены z = 1 / √2 tan x.

За исключением z вдоль отрезка ветви (−∞, −1 / e] (где интеграл не сходится), главную ветвь функции Ламберта W можно вычислить с помощью следующего интеграла:

$W\; (z)\; =\; z\; 2\; \pi \; \int \; -\; \pi \; \pi \; (1\; -\; \nu \; детская\; кроватка\; \; \nu )\; 2\; +\; \nu \; 2\; z\; +\; \nu \; csc\; \; \nu \; e\; -\; \nu \; детская\; кроватка\; \; \nu \; d\; \nu \; =\; z\; \pi \; \int \; 0\; \pi \; (1\; -\; \nu \; детская\; кроватка\; \; \nu )\; 2\; +\; \nu \; 2\; z\; +\; \nu \; csc\; \; \nu \; е\; -\; \nu \; детская\; кроватка\; \; \nu \; d\; \nu ,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; W\; (z)\; =\; \{\backslash \; frac\; \{z\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; pi\}\; ^\; \{\backslash \; pi\}\; \{\backslash \; frac\; \{\backslash \; left\; (1-\; \backslash \; nu\; \backslash \; cot\; \backslash \; nu\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; nu\; ^\; \{2\}\}\; \{z\; +\; \backslash \; nu\; \backslash \; csc\; \backslash \; nu\; e\; ^\; \{\; -\; \backslash \; nu\; \backslash \; cot\; \backslash \; nu\}\}\}\; \backslash ,\; d\; \backslash \; nu\; \backslash \backslash \; [5pt]\; =\; \{\backslash \; frac\; \{z\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; \{\backslash \; frac\; \{\backslash \; left\; (1-\; \backslash \; nu\; \backslash \; cot\; \backslash \; nu\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; nu\; ^\; \{2\}\}\; \{z\; +\; \backslash \; nu\; \backslash \; csc\; \backslash \; nu\; e\; ^\; \{-\; \backslash \; nu\; \backslash \; cot\; \backslash \; nu\}\}\}\; \backslash ,\; d\; \backslash \; nu,\; \backslash \; end\; \{align\}\}\}$

, где два интегральных выражения эквивалентны из-за симметрии подынтегрального выражения.

Неопределенные интегралы

$\int \; W\; (x)\; xdx\; =\; 1\; 2\; (1\; +\; W\; (\; x))\; 2\; +\; C.\; \int \; W\; (A\; e\; B\; x)\; dx\; =\; 1\; 2\; B\; (1\; +\; W\; (A\; e\; B\; x))\; 2\; +\; C.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; \{\backslash \; frac\; \{W\; (x)\}\; \{x\}\}\; dx\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \{\backslash \; bigl\; (\}\; 1\; +\; W\; (x)\; \{\backslash \; bigr)\}\; ^\; \{2\}\; +\; C.\; \backslash \; \backslash \; [5pt]\; \backslash \; int\; W\; \backslash \; left\; (Ae\; ^\; \{Bx\}\; \backslash \; right)\; dx\; =\; \{\backslash \; frac\; \{1\}\; \{2B\}\}\; \{\backslash \; bigl\; (\}\; 1\; +\; W\; \backslash \; left\; (Ae\; ^\; \{Bx\}\; \backslash \; right)\; \{\backslash \; bigr)\}\; ^\; \{2\}\; +\; C.\; \backslash \; end\; \{align\}\}\}$

Решение уравнений

Функция Ламберта W используется для решений, в которых неизвестные количества встречаются как в основании, так и в экспоненте, или как внутри, так и вне логарифма. Стратегия состоит в том, чтобы преобразовать такое уравнение в одну из форм ze = w, а затем решить относительно z. используя функцию W.

Например, уравнение

$3\; x\; =\; 2\; x\; +\; 2\; \{\backslash \; displaystyle\; 3\; ^\; \{x\}\; =\; 2x\; +\; 2\}$

(где x - неизвестное действительное число) может быть решено следующим образом: переписав его как

$(x\; +\; 1)\; 3\; -\; x\; =\; 1\; 2\; \iff \; (-\; x\; -\; 1)\; 3\; -\; x\; -\; 1\; =\; -\; 1\; 6\; \iff \; (ln\; \; 3)\; (-\; x\; -\; 1)\; e\; (\; пер\; \; 3)\; (-\; Икс\; -\; 1)\; =\; -\; пер\; \; 3\; 6\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; (x\; +\; 1)\; \backslash \; 3\; ^\; \{-\; x\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; \backslash \backslash \; Leftrightarrow\; \backslash \; (-\; x-1)\; \backslash \; 3\; ^\; \{-\; x-1\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{6\}\}\; \backslash \backslash \backslash \; Leftrightarrow\; \backslash \; (\backslash \; ln\; 3)\; (-\; x-1)\; \backslash \; e\; ^\; \{(\backslash \; ln\; 3)\; (-\; x-1)\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; ln\; 3\}\; \{6\}\}\; \backslash \; end\; \{align\}\}\}$

Это последнее уравнение имеет желаемую формулу, а решения для действительного x::

$(ln\; 3)\; (-\; x\; -\; 1)\; =\; W\; 0\; (-\; ln\; 3\; 6)\; или\; (ln\; \; 3)\; (-\; x\; -\; 1)\; =\; W\; -\; 1\; (-\; ln\; \; 3\; 6)\; \{\; \backslash \; Displaystyle\; (\backslash \; ln\; 3)\; (-\; x-1)\; =\; W\_\; \{0\}\; \backslash \; left\; (\{\backslash \; frac\; \{-\; \backslash \; ln\; 3\}\; \{6\}\}\; \backslash \; right)\; \backslash \; \backslash \; \backslash \; \{\backslash \; textrm\; \{или\}\}\; \backslash \; \backslash \; \backslash \; (\backslash \; ln\; 3)\; (-\; x-1)\; =\; W\; \_\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{-\; \backslash \; ln\; 3\}\; \{6\}\}\; \backslash \; right)\}$

и, таким образом:

$x\; =\; -\; 1\; -\; W\; 0\; (-\; ln\; \; 3\; 6)\; ln\; \; 3\; =\; -\; 0,7901\; 1...\; или\; x\; =\; -\; 1\; -\; W\; -\; 1\; (-\; ln\; \; 3\; 6)\; ln\; \; 3\; =\; 1,44456...\; \{\backslash \; displaystyle\; x\; =\; -1-\; \{\backslash \; frac\; \{W\_\; \{0\}\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; ln\; 3\}\; \{6\}\}\; \backslash \; right)\}\; \{\backslash \; ln\; 3\}\}\; =\; -\; 0,79011...\; \backslash \; \backslash \; \{\backslash \; textrm\; \{или\}\}\; \backslash \; \backslash \; x\; =\; -1\; -\; \{\backslash \; frac\; \{\; W\; \_\; \{-\; 1\}\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; ln\; 3\}\; \{6\}\}\; \backslash \; right)\}\; \{\backslash \; ln\; 3\}\}\; =\; 1.44456...\}$

. Как правило, решение для

$x\; =\; a\; +\; beansx\; \{\backslash \; displaystyle\; x\; =\; a\; +\; b\; \backslash ,\; e\; ^\; \{cx\}\}$

это:

$x\; =\; a\; -\; 1\; c\; W\; (-\; bceac)\; \{\backslash \; displaystyle\; x\; =\; a\; -\; \{\backslash \; frac\; \{\; 1\}\; \{c\}\}\; W\; (-bc\; \backslash ,\; e\; ^\; \{ac\})\}$

где a, b и c - комплексные константы, где b и c не равны нулю, а функция W имеет любой целочисленный порядок.

Вязкие потоки

Фронты и отложения зернистых и селевых потоков, а также фронты вязких флюидов в природных явлениях и в лабораторных экспериментах можно описать с помощью омега-функции Ламберта-Эйлера следующим образом:

$ЧАС\; (Икс)\; знак\; равно\; 1\; +\; W\; ((ЧАС\; (0)\; -\; 1)\; е\; (ЧАС\; (0)\; -\; 1)\; -\; х\; L),\; \{\backslash \; Displaystyle\; Н\; (х)\; =\; 1\; +\; W\; \backslash \; влево\; ((Н\; (0)\; -1)\; e\; ^\; \{(H\; (0)\; -1)\; -\; \{\backslash \; frac\; \{x\}\; \{L\}\}\}\; \backslash \; right),\}$

где H (x) - высота селевого потока, x - положение канала ниже по потоку, L - параметр единой модели, состоящий из нескольких физических и геометрических параметров потока, высоты потока и градиента гидравлического давления.

В потоке в трубе функция W Ламберта является частью явной формуки уравнения Коулбрука для нахождения коэффициента трения Дарси. Этот коэффициент используется для определения падения давления на прямом участке трубы, когда поток турбулентный.

Нейровизуализация

Функция Ламберта использовалась в области нейровизуализации для связи церебрального кровотока и потребления кислорода в вокселе мозга до соответствующего сигнала, зависящего от уровня оксигенации крови (жирный шрифт).

Химическая инженерия

Функция Ламберта использовалась в области химической инженерии для моделирования пористой толщины электродной пленки в суперконденсаторе на основе стеклоуглерода для электрохимического накопления энергии. Функция Ламберта W оказалась точным решением для процесса термической активации в газовой фазе, когда рост углеродной пленки и горения одной и той же пленки конкурируют друг с другом.

Материаловедение

Ламберт Функция использовалась в области роста эпитаксиальной пленки для определения критической дислокации начальной толщины пленки. Это расчетная толщина эпитаксиальной пленки, согласно термодинамическим принципам в пленке будут развиваться кристаллографические дислокации, чтобы минимизировать запасенную в пленках упругую энергию. Перед применением метода Ламберта W для решения этой задачи необходимо определить критическую толщину решения неявного уравнения. Ламберт W с легкостью превращает его в явное уравнение для аналитической обработки.

Пористая среда

Функция Ламберта W использовалась в области течения жидкости в пористой среде для моделирования наклона граница раздела двух гравитационно разделенных жидкостей в однородном наклонном пористом слое с постоянным падением и толщиной, где более тяжелая жидкость, закачиваемая в нижний конец, вытесняет более легкую жидкость, которая производит той же скоростью, из верхнего конца. Основная ветвь решения соответствует стабильному смещению, а ветвь −1 применяется, если смещение нестабильно, когда более тяжелая жидкость течет под более легкой.

Числа Бернулли и род Тодда

Уравнение (связано с производственными функциями чисел Бернулли и рода Тодда ):

$Y\; =\; X\; 1\; -\; e\; X\; \{\backslash \; displaystyle\; Y\; =\; \{\backslash \; frac\; \{X\}\; \{1-\; e\; ^\; \{X\}\}\}\}$

можно решить с помощью двух ветвей W 0 и W −1:

Это приложение показывает, что разность ветвлений функции W может быть для решения других трансцендентных уравнений.

Статистика

Центроид гистограмм, определенно симметризованной дивергенции Кульбака - Лейблера (также называемой дивергенцией Джефф), имеет замкнутую форму с использованием функций Ламберта W.

Точные решения уравнения Уравнение Шредингера

Функция W Ламберта появляется в квантово-механическом потенциале, который дает пятое - после гармонического осциллятора плюс центробежный, кулоновского плюс обратный квадрат, Морса и - точное решение стационарного одномерного уравнения Шредингера в терминах конфлюэнтные гипергеометрические функции. Потенциал задается как

$V\; =\; V\; 0\; 1\; +\; W\; (e\; -\; x\; \sigma ).\; \{\backslash \; displaystyle\; V\; =\; \{\backslash \; frac\; \{V\_\; \{0\}\}\; \{1\; +\; W\; \backslash \; left\; (e\; ^\; \{-\; \{\backslash \; frac\; \{x\}\; \{\backslash \; sigma\}\}\}\}\}\; \backslash \; right)\}\}.\}$

Особенность решения состоит в том, что каждый из двух фундаментальных решений, составляющих общее решение уравнения Шредингера, задается комбинацией двух конфлюэнтных гипергеометрических функций аргумента, пропорционального

$z\; =\; W\; (e\; -\; x\; \sigma ).\; \{\backslash \; displaystyle\; z\; =\; W\; \backslash \; left\; (e\; ^\; \{-\; \{\backslash \; frac\; \{x\}\; \{\backslash \; sigma\}\}\}\}\; \backslash \; right).\}$

Функция W Ламберта также представляет в точном решении для энергии связанного состояния одномерное уравнение Шредингера с двойным дельта-потенциалом.

Точные решения уравнений вакуума Эйнштейна

В решении уравнений вакуума Эйнштейна с метрикой Шварцшильда требуется функция W для перехода от координат Эддингтона - Финкельштейна к координатам Шварцшильда. По этой причине он также появляется при построении координат Крускала – Секереса.

Резонансы потенциала дельта-оболочки

s-волновые резонансы потенциала дельта-оболочки можно записать точно в терминах функции Ламберта W.

Термодинамическое равновесие

Если в реакции участвуют реагенты и продукты, имеющие теплоемкость, постоянную с температурой, то константа равновесия K подчиняется

$ln\; \; K\; =\; a\; T\; +\; b\; +\; c\; ln\; \; T\; \{\backslash \; displaystyle\; \backslash \; ln\; K\; =\; \{\backslash \; frac\; \{a\}\; \{T\}\}\; +\; b\; +\; c\; \backslash \; ln\; T\}$

для некоторых констант a, b, и c. Когда c (равно ΔC p / R) не равно нулю, мы можем найти значение или значения T, где K равно заданному значению, следующим образом, где мы используем L для ln T.

$-\; a\; =\; (b\; -\; ln\; \; K)\; T\; +\; c\; T\; ln\; \; T\; =\; (b\; -\; ln\; \; K)\; e\; L\; +\; c\; L\; e\; L\; -\; ac\; =\; (b\; -\; ln\; \; K\; c\; +\; L)\; e\; L\; -\; aceb\; -\; ln\; \; K\; c\; =\; (L\; +\; b\; -\; ln\; \; K\; c)\; e\; L\; +\; b\; -\; ln\; \; K\; c\; L\; =\; W\; (-\; aceb\; -\; ln\; \; K\; c)\; +\; ln\; \; K\; -\; bc\; T\; =\; exp\; \; (W\; (-\; aceb\; -\; ln\; \; K\; c)\; +\; ln\; \; K\; -\; bc).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; -a\; =\; (b-\; \backslash \; ln\; K)\; T\; +\; cT\; \backslash \; ln\; T\; \backslash \backslash \; =\; (b-\; \backslash \; ln\; K)\; e\; ^\; \{L\}\; +\; cLe\; ^\; \{L\}\; \backslash \backslash \; [\; 5pt]\; -\; \{\backslash \; frac\; \{a\}\; \{c\}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{b-\; \backslash \; ln\; K\}\; \{c\}\}\; +\; L\; \backslash \; right)\; e\; ^\; \{L\}\; \backslash \backslash \; [5pt]\; -\; \{\backslash \; frac\; \{a\}\; \{c\}\}\; e\; ^\; \{\backslash \; frac\; \{b-\; \backslash \; ln\; K\}\; \{c\}\}\; =\; \backslash \; left\; (L\; +\; \{\backslash \; frac\; \{b-\; \backslash \; ln\; K\}\; \{c\}\}\; \backslash \; right)\; e\; ^\; \{\; L\; +\; \{\backslash \; frac\; \{b-\; \backslash \; ln\; K\}\; \{c\}\}\}\; \backslash \backslash \; [5pt]\; L\; =\; W\; \backslash \; left\; (-\; \{\backslash \; frac\; \{a\}\; \{c\}\}\; e\; ^\; \{\backslash \; frac\; \{b-\; \backslash \; ln\; K\})\; \{c\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{\backslash \; ln\; Kb\}\; \{c\}\}\; \backslash \backslash \; [5pt]\; T\; =\; \backslash \; exp\; \backslash \; left\; (W\; \backslash \; left\; (-\; \{\backslash \; frac\; \{a\}\; \{c\}\}\; e\; ^\; \{\; \backslash \; frac\; \{b-\; \backslash \; ln\; K\}\; \{c\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{\backslash \; ln\; Kb\}\; \{c\}\}\; \backslash \; right).\; \backslash \; end\; \{align\}\}\}$

Если a и c имеют одинаковые знак будет либо два решения, либо ни одного (или одно, если аргумент W точно равен −1 / e). (Верхнее решение может не иметь отношения.) Если они имеют противоположные знаки, будет одно решение.

Соответствие AdS / CFT

Классические поправки конечного размера к дисперсионным соотношениям пиков и могут быть выражены в терминах функций Ламберта W.

Эпидемиология

В пределе t → ∞ модели SIR соотношение восприимчивых и выздоровевших людей имеет решение в терминах функций Ламберта W.

Определение времени полета снаряда

Общее время полета снаряда, которое испытывает сопротивление воздуха, в точной форме с использованием функций W Ламберта, пропорциональное его скорость , может быть определено.

Стандартная функция Ламберта W выражает точные решения трансцендентных алгебраических уравнений (по x) в форме:

$e\; -\; cx\; =\; a\; 0\; (x\; -\; r)\; \{\backslash \; displaystyle\; e\; ^\; \{\; -\; cx\}\; =\; a\_\; \{0\}\; (xr)\}$

(1)

где a 0, c и r - действительные константы. Решение:

$x\; =\; r\; +\; 1\; c\; W\; (c\; e\; -\; c\; r\; a\; 0).\; \{\backslash \; displaystyle\; x\; =\; r\; +\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; W\; \backslash \; left\; (\{\backslash \; frac\; \{c\; \backslash ,\; e\; ^\; \{-\; cr\}\}\; \{a\_\; \{0\}\}\}\; \backslash \; right).\}$

Обобщения функции Ламберта W включает:

• Приложение к общей теории относительности и квантовой механике (квантовой гравитации ) в более низких измерениях, фактически ссылка (неизвестно до 2007 г.) ​​между этими двумя областями, где правая часть (1) заменена квадратичным многочленом от x:

$e\; -\; cx\; =\; a\; 0\; (x\; -\; r\; 1)\; (x\; -\; r\; 2),\; \{\backslash \; displaystyle\; e\; ^\; \{\; -\; cx\}\; =\; a\_\; \{0\}\; \backslash \; left\; (x-r\_\; \{1\}\; \backslash \; right)\; \backslash \; left\; (x-r\_\; \{2\}\; \backslash \; right),\}$

(2)

где r 1 и r 2 - действительные различные константы, корни квадратичного многочлена. Здесь решение - это функция с одним аргументом x, но такие термины, как r i и a 0, являются действующими функциями. В этом отношении обобщение напоминает функцию гипергеометрическую и функцию G Мейера, но принадлежит к другому классу функций. Когда r 1 = r 2, обе стороны (2) могут быть разложены на множители и уменьшены до (1), и, таким образом, решение сводится к стандартному решению W-функции.. Уравнение (2) выражает уравнение, определяющее поле дилатон, из которого выводится метрика R = T или линейной задачи двух тел гравитации в 1 + 1 измерениях (одно пространственное измерение и одно временное измерение измерение измерения для случая неравных масс покоя, а также собственных сил квантово-механической двухъямной модели дельта-функции Дирака для неравных зарядов в одном измерении.

• Аналитический анализ решения собственных энергий частного случая квантово-механической задачи трех тел, а именно (трехмерной) молекулы-иона водорода. Здесь правая часть (1) заменена отношением многочленов бесконечного порядка по x:

$e\; -\; cx\; =\; a\; 0\; \prod \; i\; =\; 1\; \infty \; (x\; -\; ri)\; \prod \; i\; =\; 1\; \infty \; (x\; -\; си)\; \{\backslash \; displaystyle\; e\; ^\; \{-\; cx\}\; =\; a\_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{\backslash \; infty\}\; (x-r\_\; \{i\})\}\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{\; \backslash \; infty\}\; (x-s\_\; \{i\})\}\}\}$

(3)

где r i и s i - различные действительные константы, а x является функцией собственной энергии и межъядерного расстояния R. Уравнение (3) с его специальными случаями, выраженными в (1) и (2), относится к большому классу дифференциальные уравнения с запаздыванием. Г. Понятие «ложной производной» Х. Харди обеспечивает точные множественные корни для частных случаев (3).

Применения W-функции Ламберта в фундаментальных физических проблемах не исчерпывает даже для стандартного случая, выраженного в (1), как это было недавно замечено в области атомной, молекулярной и оптической физики.

• Графики W-функции Ламберта на комплексной плоскости
• 

  z = Re (W 0 (x + iy))

• 

  z = Im (W 0 (x + iy))

• 

  z = | W 0 (x + iy) |

• 

  Наложение предыдущих трех графиков

Функция W может быть аппроксимирована использованием метода Ньютона с последовательными приближениями к w = W (z) (поэтому z = we)

$wj\; +\; 1\; =\; wj\; -\; wjewj\; -\; zewj\; +\; wjewj.\; \{\backslash \; Displaystyle\; w\_\; \{\; j\; +\; 1\}\; =\; w\_\; \{j\}\; -\; \{\backslash \; frac\; \{w\_\; \{j\}\; e\; ^\; \{w\_\; \{j\}\}\; -\; z\}\; \{e\; ^\; \{w\_\; \{j\}\}\; +\; w\_\; \{j\}\; e\; ^\; \{w\_\; \{j\}\; \}\}\}.\}$

Функция W также может быть аппроксимирована использованием метода Галлея,

$wj\; +\; 1\; =\; wj\; -\; wjewj\; -\; zewj\; (wj\; +\; 1)\; -\; (wj\; +\; 2)\; (wjewj\; -\; z)\; 2\; wj\; +\; 2\; \{\backslash \; displaystyle\; w\_\; \{j\; +\; 1\}\; =\; w\_\; \{j\}\; -\; \{\backslash \; frac\; \{w\_\; \{j\}\; e\; ^\; \{w\_\; \{j\}\}\; -\; z\}\; \{e\; ^\; \{w\_\; \{j\}\}\; \backslash \; left\; (w\_\; \{\; j\}\; +1\; \backslash \; right)\; -\; \{\backslash \; dfrac\; \{\backslash \; left\; (w\_\; \{j\}\; +2\; \backslash \; right)\; \backslash \; left\; (w\_\; \{j\}\; e\; ^\; \{w\_\; \{j\}\}\; -\; z\; \backslash \; right)\}\; \{2w\_\; \{j\}\; +\; 2\}\}\}\}\}$

приведено у Corless et al. для вычислений W.

Функция Lambert W реализована как LambertWв Maple, lambertwв GP (и glambertWв PARI ), lambertwв Matlab, также lambertwв Octave с пакетом specfun, как lambert_wв Maxima, как ProductLog(с скрытым псевдонимом LambertW) в Mathematica, как lambertwв пакете специальных функций Python scipy, как LambertWв модуле Perl ntheoryи как gsl_sf_lambert_W0, gsl_sf_lambert_Wm1функции в разделе специальные функции Научной библиотеки GNU (GSL). В библиотеках Boost C ++ используются следующие вызовы: lambert_w0, lambert_wm1, lambert_w0_primeи lambert_wm1_prime. В R функция Ламберта W реализована как функции lambertW0и lambertWm1в lamWпакете.

Код C ++ для всех ветвей сложной функции Ламберта W доступно на домашней странице Иштвана Мезо.

• Омега-функция Райта
• Трехчленное уравнение Ламберта
• Теорема об обращении Лагранжа
• Экспериментальная математика
• Метод Холстейна - Херринга
• R = T модель
• π-лемма Росса

• Corless, R.; Gonnet, G.; Заяц, Д.; Джеффри, Д.; Кнут, Дональд (1996). «О функции W Ламберта» (PDF). Успехи в вычислительной математике. 5 : 329–359. DOI : 10.1007 / BF02124750. ISSN 1019-7168. S2CID 29028411. Архивировано из оригинального (PDF) 14 декабря 2010 г. Проверено 10 марта 2007 г.
• Шапо-Блондо, Ф.; Монир, А. (2002). «Оценка W-функций Ламберта и ее применение для генерации обобщенного гауссовского шума с показателем 1/2» (PDF). IEEE Trans. Сигнальный процесс. 50 (9). DOI : 10.1109 / TSP.2002.801912. Архивировано из оригинального (PDF) 28 марта 2012 г. Проверено 10 марта 2004 г.
• Фрэнсис; и другие. (2000). «Количественная общая теория периодического дыхания». Тираж. 102 (18): 2214–21. CiteSeerX 10.1.1.505.7194. doi : 10.1161 / 01.cir.102.18.2214. PMID 11056095. S2CID 14410926.(функция Ламберта используется для решения дифференциальной динамики при заболеваниях человека.)
• Hayes, B. (2005). «Почему W?» (PDF). Американский ученый. 93 (2): 104–108. doi : 10.1511 / 2005.2.104.
• Рой, Р.; Олвер, Ф. В. Дж. (2010), «W-функция Ламберта», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз У. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
• Стюарт, Шон М. (2005). «Новая элементарная функция для наших учебных программ?» (PDF). Австралийский старший математический журнал. 19 (2): 8–26. ISSN 0819-4564. ЭРИК EJ720055. Краткое содержание.
• Веберик, Д., «Развлечение с функцией Ламберта W (x)» arXiv: 1003.1628 (2010) ; Веберик, Д. (2012). «W-функция Ламберта для приложений в физике». Компьютерная физика. 183 (12): 2622–2628. arXiv : 1209.0735. Bibcode : 2012CoPhC.183.2622V. doi : 10.1016 / j.cpc.2012.07.008. S2CID 315088.
• Чатзигеоргиу, И. (2013). «Границы функции Ламберта и их применение для анализа сбоев взаимодействия пользователей». Письма связи IEEE. 17 (8): 1505–1508. arXiv : 1601.04895. DOI : 10.1109 / LCOMM.2013.070113.130972. S2CID 10062685.

Викискладе есть медиафайлы, связанные с функцией Ламберта W.

• Цифровая библиотека национального института науки и технологий - Lambert W
• MathWorld - W-функция Ламберта
• Вычисление W-функции Ламберта
• Корлесс и др. Заметки об исследовании Lambert W.
• GPL реализация C ++ с итерацией Галлея и Фрича.
• Специальные функции из Научной библиотеки GNU - GSL