Связанное состояние

редактировать

Система, в которой частица подвержена такому потенциалу, что частица имеет тенденцию оставаться локализованной в одной или нескольких областях пространства

В квантовой физике, связанное состояние - это квантовое состояние частицы, подверженной потенциалу, так что частица имеет тенденцию оставаться локализованной в одной или нескольких областях пространства. Потенциал может быть внешним или быть результатом присутствия другой частицы; в последнем случае можно эквивалентно определить связанное состояние как состояние, представляющее две или более частицы, энергия взаимодействия которых превышает полную энергию каждой отдельной частицы. Одно из следствий состоит в том, что при условии, что потенциал исчезает на бесконечности, состояния с отрицательной энергией должны быть связаны. В общем, энергетический спектр набора связанных состояний дискретен, в отличие от свободных частиц, которые имеют непрерывный спектр.

Хотя и не связанные состояния в строгом смысле, метастабильные состояния с чистой положительной энергией взаимодействия, но с большим временем распада также часто считаются нестабильными связанными состояниями и называются «квазисвязанными состояниями». Примеры включают определенные радионуклиды и электреты.

В релятивистской квантовой теории поля устойчивое связанное состояние n частиц с массами ${mk } k = 1 n {\ displaystyle \ {m_ {k} \} _ {k = 1} ^ {n}}$ ${\ displaystyle \ {m_ {k} \} _ {k = 1} ^ {n} }$ соответствует полюсу в S- матрица с энергией центра масс меньше $∑ kmk {\ displaystyle \ textstyle \ sum _ {k} m_ {k}}$ ${\ displaystyle \ textstyle \ sum _ {k} m_ {k}}$ . нестабильное связанное состояние проявляется как полюс с комплексной энергией центра масс.

Содержание

1 Примеры
2 Определение
3 Свойства
- 3.1 Состояния с привязкой к положению
4 Требования
5 См. Также
6 Ссылки

Примеры

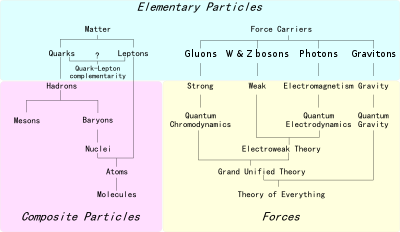
Обзор различных семейств элементарных и составных частиц и теорий, описывающих их взаимодействия

A протон и электрон могут двигаться отдельно; когда они это делают, полная энергия центра масс положительна, и такую пару частиц можно описать как ионизированный атом. Как только электрон начинает "вращаться" вокруг протона, его энергия становится отрицательной и образуется связанное состояние, а именно атом водорода. Только связанное состояние с самой низкой энергией, основное состояние, является стабильным. Другие возбужденные состояния являются нестабильными и будут распадаться на стабильные (но не другие нестабильные) связанные состояния с меньшей энергией, испуская фотон.
A позитроний «атом» является нестабильным связанное состояние электрона и позитрона. Он распадается на фотоны.
Любое состояние в квантовом гармоническом осцилляторе связано, но имеет положительную энергию. Обратите внимание, что $lim x → ± ∞ V QHO (x) = ∞ {\ displaystyle \ lim _ {x \ to \ pm \ infty} {V _ {\ text {QHO}} (x)} = \ infty}$ ${\ displaystyle \ lim _ {x \ to \ pm \ infty } {В _ {\ текст {QHO}} (х)} = \ infty}$ , поэтому ниже не применяется.
A ядро является связанным состоянием протонов и нейтронов (нуклоны ).
Сам протон является связанным состоянием трех кварков (два вверх и один внизу ; один красный, один зеленый и один синий ). Однако, в отличие от атома водорода, отдельные кварки никогда не могут быть изолированы. См. ограничение.
Модели Хаббарда и Джейнса-Каммингса-Хаббарда (JCH) поддерживают аналогичные связанные состояния. В модели Хаббарда два отталкивающих бозонных атома могут образуют связанную пару в оптической решетке . Гамильтониан JCH также поддерживает два- поляритонных связанных состояния, когда взаимодействие фотон-атом достаточно сильное.

Определение

Пусть H - комплексное разделимое гильбертово пространство, $U = {U (t) ∣ t ∈ R} {\ displaystyle U = \ lbrace U (t) \ mid t \ in \ mathbb {R} \ rbrace}$ $U = \ lbrace U (t) \ mid t \ in {\ mathbb {R}} \ rbrace$ - однопараметрическая группа унитарных операторов на H и $ρ = ρ (t 0) { \ displaystyle \ rho = \ rho (t_ {0})}$ $\ rho = \ rho (t_ {0})$ быть статистическим оператором на H. Пусть A будет наблюдаемым на H и $μ (A, ρ) {\ displaystyle \ mu (A, \ rho)}$ $\ mu (A, \ rho)$ - индуцированное распределение вероятностей A относительно ρ на борелевской σ-алгебре из $Р {\ Displaystyle \ mathbb {R}}$ $\ mathbb {R}$ . Тогда эволюция ρ, индуцированная U, ограничена относительно A, если $lim R → ∞ sup t ≥ t 0 μ (A, ρ (t)) (R>R) = 0 { \ Displaystyle \ lim _ {R \ rightarrow \ infty} {\ sup _ {t \ geq t_ {0}} {\ mu (A, \ rho (t)) (\ mathbb {R} _ {>R})} } = 0}$ $\lim _{R\rightarrow \infty }{\sup _{t\geq t_{0}}{\mu (A,\rho (t))(\mathbb {R} _{>R})}} = 0$ , где $R>R = {x ∈ R ∣ x>R} {\ displaystyle \ mathbb {R} _ {>R} = \ lbrace x \ in \ mathbb {R } \ mid x>R \ rbrace}$ ${\mathbb {R}}_{{>R}} = \ lbrace x \ in {\ mathbb {R}} \ mid x>R \ rbrace$ .

Более неформально, связанное состояние содержится в ограниченной части спектр A. Для конкретного примера: пусть $H = L 2 (R) {\ displaystyle H = L ^ {2} (\ mathbb {R})}$ $H = L ^ {2} ({\ mathbb {R}})$ и пусть A будет положением. Для данных с компактной опорой $ρ = ρ (0) ∈ H {\ displaystyle \ rho = \ rho (0) \ in H}$ $\ rho = \ rho (0) \ in H$ и $[- 1, 1] ⊆ S upp ( ρ) {\ displaystyle [-1,1] \ substeq \ mathrm {Supp} (\ rho)}$ $[-1,1] \ substeq {\ mathrm {Supp}} (\ rho)$ .

Если эволюция состояния ρ "постоянно перемещает этот волновой пакет вправо", например если $[t - 1, t + 1] ∈ S upp (ρ (t)) {\ displaystyle [t-1, t + 1] \ in \ mathrm {Supp} (\ rho (t))}$ $[t-1, t + 1] \ in {\ mathrm { Supp}} (\ rho (t))$ для всех $t ≥ 0 {\ displaystyle t \ geq 0}$ $t \ geq 0$ , тогда ρ не является связанным состоянием относительно позиции.
Если $ρ {\ displaystyle \ rho}$ $\ rho$ не меняется во времени, т.е. $ρ (t) = ρ {\ displaystyle \ rho (t) = \ rho}$ $\ rho (t) = \ rho$ для всех $t ≥ 0 {\ displaystyle t \ geq 0}$ $t \ geq 0$ , тогда $ρ {\ displaystyle \ rho}$ $\ rho$ привязан к положению.
Дополнительно в общем случае: если эволюция состояния ρ «просто перемещает ρ внутрь ограниченной области», то ρ ограничена относительно позиции.

Свойства

Пусть A имеет область измерения пространства меры $(X; μ) {\ Displaystyle (X; \ mu)}$ ${\ displaystyle (X; \ mu)}$ . Квантовая частица находится в связанном состоянии, если она никогда не обнаруживается «слишком далеко от любой конечной области $R ⊆ X {\ displaystyle R \ substeq X}$ ${\ Displaystyle R \ substeq X}$ », то есть с использованием представления волновой функции,

$0 = lim R → ∞ P (частица, измеренная внутри X ∖ R) = lim R → ∞ ∫ X ∖ R | ψ (x) | 2 d μ (Икс) {\ Displaystyle {\ begin {align} 0 = \ lim _ {R \ to \ infty} {\ mathbb {P} ({\ text {частица, измеренная внутри}} X \ setminus R)} \ \ = \ lim _ {R \ to \ infty} {\ int _ {X \ setminus R} | \ psi (x) | ^ {2} \, d \ mu (x)} \ end {align}}}$ ${\ displaystyle {\ begin {align} 0 = \ lim _ {R \ to \ infty} {\ mathbb {P} ({\ text {частица, измеренная внутри}} X \ setminus R)} \\ = \ lim _ {R \ to \ infty} {\ int _ {X \ setminus R} | \ psi (x) | ^ {2} \, d \ mu (x)} \ end {выровнено }}}$

Следовательно, $∫ X | ψ (x) | 2 d μ (x) {\ displaystyle \ int _ {X} {| \ psi (x) | ^ {2} \, d \ mu (x)}}$ ${\ displaystyle \ int _ {X} {| \ psi (x) | ^ {2} \, d \ mu (x)}}$ конечно. Другими словами, состояние является связанным состоянием тогда и только тогда, когда оно конечно нормализуемо.

Поскольку конечно нормализуемые состояния должны находиться в дискретной части спектра, связанные состояния должны находиться внутри дискретной части. Однако, как указывали Нейман и Вигнер, связанное состояние может иметь свою энергию, расположенную в непрерывном спектре. В этом случае связанные состояния по-прежнему являются частью дискретной части спектра, но отображаются в спектральной мере как массы Дирака.

Состояния с привязкой к положению

Учитывайте одночастичное уравнение Шредингера. Если состояние имеет энергию $E < max ⁡ ( lim x → ∞ V ( x), lim x → − ∞ V ( x)) {\displaystyle E<\operatorname {max} {\left(\lim _{x\to \infty }{V(x)},\lim _{x\to -\infty }{V(x)}\right)}}$ ${\ displaystyle E <\ operatorname {max} {\ left (\ lim _ {x \ to \ infty} {V (x)}, \ lim _ {x \ to - \ infty} {V (x)} \ right)}}$ , тогда волновая функция ψ удовлетворяет для некоторого $X>0 {\ displaystyle X>0}$ $X>0$

ψ ′ ′ ψ = 2 м ℏ 2 (V (x) - E)>0 для x>X {\ displaystyle {\ frac {\ psi ^ {\ prime \ prime}} {\ psi}} = {\ frac {2m} {\ hbar ^ {2}}} (V (x) -E)>0 {\ text {for}} x>X}

{\frac {\psi ^{\prime \prime }}{\psi }}={\frac {2m}{\hbar ^{2}}}(V(x)-E)>0 {\ text {for}} x>X

, так что ψ экспоненциально подавляется при больших x. Следовательно, состояния с отрицательной энергией связаны, если V обращается в нуль на бесконечности.

Требования

A бозон с массой m χ, опосредующий слабосвязанное взаимодействие, дает потенциал взаимодействия типа Юкавы,

V (г) = ± α χ re - р λ χ {\ Displaystyle V (r) = \ pm {\ frac {\ alpha _ {\ chi}} {r}} e ^ {- {\ frac {r} {\ lambda \! \! \! {\ frac {} {\}} _ {\ chi}}}}}

{\ displaystyle V (r) = \ pm {\ frac {\ alpha _ {\ chi}} {r}} e ^ {- {\ frac {r} {\ lambda \! \! \! {\ frac {} {\}} _ {\ chi}}}}}

где $α χ = g 2/4 π {\ displaystyle \ alpha _ {\ chi} = g ^ {2} / 4 \ pi}$ ${\ displaystyle \ alpha _ {\ chi} = g ^ {2} / 4 \ pi}$ , g - калибровочная константа связи, а ƛ i = ℏ / m i c - уменьшенная длина волны Комптона. скалярный бозон создает универсально притягивающий потенциал, тогда как вектор притягивает частицы к античастицам, но отталкивает как пары. Для двух частиц с массой m 1 и m 2, радиус Бора системы становится

a 0 = λ _ 1 + λ _ 2 α χ {\ displaystyle a_ {0} = {\ frac {{\ lambda \! \! \! ^ {{} ^ {\ underline {\ \}}}} _ {1} + {\ lambda \! \! \ ! ^ {{} ^ {\ underline {\ \}}}} _ {2}} {\ alpha _ {\ chi}}}}

{\ displaystyle a_ {0} = {\ frac {{\ lambda \! \! \! ^ {{} ^ {\ underline {\ \}}}} _ {1} + {\ lambda \! \! \! ^ {{} ^ {\ Underline {\ \}}}} _ {2}} {\ alpha _ {\ chi}}}}

и дает безразмерное число

D = λ _ χ a 0 знак равно α χ λ _ χ λ _ 1 + λ _ 2 знак равно α χ м 1 + м 2 м χ {\ displaystyle D = {\ frac {{\ lambda \! \! \! ^ {{} ^ {\ underline { \ \}}}} _ {\ chi}} {a_ {0}}} = \ alpha _ {\ chi} {\ frac {{\ lambda \! \! \! ^ {{} ^ {\ underline {\ \}}}} _ {\ chi}} {{\ lambda \! \! \! ^ {{} ^ {\ underline {\ \}}}} _ {1} + {\ lambda \! \! \! ^ {{} ^ {\ underline {\ \}}}} _ {2}}} = \ alpha _ {\ chi} {\ frac {m_ {1} + m_ {2}} {m _ {\ chi}} }}

{\ displaystyle D = {\ frac {{\ lambda \! \! \! ^ {{} ^ {\ Underline {\ \}}}} _ {\ chi}} {a_ {0}}} = \ alpha _ {\ chi} {\ frac {{\ lambda \! \! \! ^ {{} ^ {\ Underline {\ \}}}} _ {\ chi}} {{\ лямбда \! \! \! ^ {{} ^ {\ underline {\ \}}}} _ {1} + {\ lambda \! \! \! ^ {{} ^ {\ underline {\ \}}} } _ {2}}} = \ alpha _ {\ chi} {\ frac {m_ {1} + m_ {2}} {m _ {\ chi}}}}

Чтобы первое связанное состояние вообще существовало, $D ≳ 0.8 {\ displaystyle D \ gtrsim 0.8}$ ${\ displaystyle D \ gtrsim 0.8}$ . Поскольку фотон не имеет массы, D бесконечно для электромагнетизма. Для слабого взаимодействия масса Z-бозона составляет 91,1876 ± 0,0021 ГэВ / c, что предотвращает образование связанных состояний между большинством частиц, поскольку она в 97,2 раза больше, чем масса протона и в 178000 раз больше массы электрона.

Однако обратите внимание, что если взаимодействие Хиггса не нарушает электрослабую симметрию на шкале электрослабого взаимодействия, то SU (2) слабое взаимодействие станет ограничивающим.