Тест соотношения

редактировать

В математике тест отношения является тестом (или «критерий») сходимости серии

∑ n = 1 ∞ an, {\ displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n },}

\sum _{{n=1}}^{\infty }a_{n},

, где каждый член является действительным или комплексным числом, а n отличен от нуля, когда n велико. Тест был впервые опубликован Жаном ле Рондом Даламбером и иногда известен как критерий отношения Даламбера или критерий отношения Коши .

Содержание

1 Тест
2 Примеры
- 2.1 Сходящиеся, потому что L < 1
- _1 ">2.2 Дивергентные, потому что L>1
- 2.3 Неубедительные, потому что L = 1
3 Доказательство
4 Расширения для L = 1
- 4.1 Иерархия Де Моргана
  - 4.1.1 1. Тест отношения Даламбера
  - 4.1.2 2. Тест Раабе
    - 4.1.2.1 Доказательство теста Раабе
  - 4.1.3 3. Тест Бертрана
  - 4.1.4 4. Расширенный тест Бертрана
  - 4.1.5 5. Тест Гаусса
  - 4.1.6 6. Тест Куммера
    - 4.1.6.1 Особые случаи
    - 4.1.6.2 Доказательство теста Куммера
- 4,2 Тест второго отношения
- 4,3 $m {\ displaystyle m}$ $m$ тест отношения
- 4,4 $φ {\ displaystyle \ varphi}$ $\varphi$ -ratio тест
5 См. также
6 Сноски
7 Ссылки

Тест

Диаграмма принятия решений для теста отношения

В обычной форме теста используется предел

L = lim n → ∞ | an + 1 an |. {\ Displaysty le L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |.}

L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|.

(1)

Соотношение тест утверждает, что:

если L < 1 then the series сходится абсолютно; ;
если L>1, то серия расходится; ;
если L = 1 или предел не существует, тогда тест неубедителен, потому что существуют как сходящиеся, так и расходящиеся ряды, которые удовлетворяют этому случаю.

Можно сделать тест отношения применимым к определенным случаям, когда предел L не существует, если предел выше и предел ниже используются. Критерии тестирования также могут быть уточнены, так что иногда проверка оказывается окончательной даже при L = 1. В частности, пусть

R = lim sup | а п + 1 а п | {\ Displaystyle R = \ lim \ sup \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}

R = \lim\sup \left|\frac{a_{n+1}}{a_n}\right|

r = lim inf | а п + 1 а п | {\ displaystyle r = \ lim \ inf \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}

r = \lim\inf \left|\frac{a_{n+1}}{a_n}\right|

Тогда тест соотношения утверждает, что:

если R < 1, the series converges absolutely;
если r>1, ряд расходится;
если $| а п + 1 а п | ≥ 1 {\ displaystyle \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | \ geq 1}$ $\ left | \ frac {a_ {n + 1}} {a_n} \ right | \ ge 1$ для всех больших n (независимо от значения r), ряд также расходится; это потому, что $| а п | {\ displaystyle | a_ {n} |}$ $|a_n|$ не равно нулю и увеличивается, и, следовательно, n не приближается к нулю;
в противном случае тест не дает результатов.

Если предел L в (1) существует, мы должны иметь L = R = r. Таким образом, исходный тест соотношения является более слабой версией усовершенствованного.

Примеры

сходятся, потому что L < 1

Рассмотрим ряд

∑ n = 1 ∞ nen {\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {n} {e ^ {n}}}}

\sum_{n=1}^\infty\frac{n}{e^n}

Применяя критерий отношения, вычисляют предел

L = lim n → ∞ | а п + 1 а п | = lim n → ∞ | п + 1 е п + 1 н е п | = 1 e < 1. {\displaystyle L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {n+1}{e^{n+1}}}{\frac {n}{e^{n}}}}\right|={\frac {1}{e}}<1.}

L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|=\lim _{{n\to \infty }}\left|{\frac {{\frac {n+1}{e^{{n+1}}}}}{{\frac {n}{e^{n}}}}}\right|={\frac {1}{e}}<1.

Поскольку этот предел меньше 1, ряд сходится.

расходится, потому что L>1

Рассмотрим ряд

∑ n = 1 ∞ e n n. {\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {e ^ {n}} {n}}.}

\sum_{n=1}^\infty\frac{e^n}{n}.

Помещаем это в тест соотношения:

L = lim n → ∞ | а п + 1 а п | = lim n → ∞ | e n + 1 n + 1 e n n | = е>1. {\ displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | = \ lim _ {n \ to \ infty} \ left | {\ frac {\ frac {e ^ {n + 1}} {n + 1}} {\ frac {e ^ {n}} {n}}} \ right | = e>1.}

L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|=\lim _{{n\to \infty }}\left|{\frac {{\frac {e^{{n+1}}}{n+1}}}{{\frac {e^{n}}{n}}}}\right|=e>1.

Таким образом, ряд расходится.

Неубедительно, потому что L = 1

Рассмотрим три ряда

∑ n = 1 ∞ 1, {\ displaystyle \ sum _ {n = 1} ^ {\ infty} 1,}

\sum_{n=1}^\infty 1,

∑ n = 1 ∞ 1 n 2, {\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {2}}},}

\ sum _ {{n = 1}} ^ {\ infty} {\ frac {1} {n ^ {2} }},

∑ N = 1 ∞ (- 1) n + 1 n. {\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n + 1}} {n} }.}

\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}.

Первый ряд (1 + 1 + 1 + 1 + ⋯ ) расходится, второй (центральный в Базельской проблеме ) сходится абсолютно и третий (чередующийся гармонический ряд ) сходится условно. Тем не менее, пословные отношения величин $| an + 1 an | {\ displaystyle \ left | {\ frac {a_ {n + 1}} {a_ {n}} } \ right |}$ $\ left | \ frac {a_ {n + 1}} {a_n} \ справа |$ из трех серий соответственно равны $1, {\ displaystyle 1,}$ $1,$ $n 2 (n + 1) 2 {\ displaystyle {\ frac {n ^ {2 }} {(n + 1) ^ {2}}}}$ $\ frac {n ^ 2} {(n + 1) ^ 2}$ и $nn + 1 {\ displaystyle {\ frac {n} {n + 1}}}$ $\frac{n}{n+1}$ . Итак, во всех трех случаях предел $lim n → ∞ | а п + 1 а п | {\ displaystyle \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$ $\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|$ равно 1. Это показывает, что когда L = 1, ряды могут сходиться или расходиться, и, следовательно, исходный тест отношения не дает результатов. В таких случаях требуются более точные тесты для определения сходимости или расхождения.

Доказательство

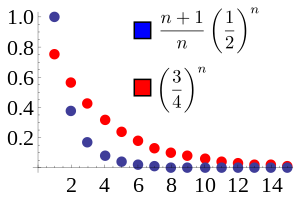
В этом примере отношение соседних членов в синей последовательности сходится к L = 1/2. Выбираем r = (L + 1) / 2 = 3/4. Тогда синяя последовательность преобладает над красной последовательностью r для всех n ≥ 2. Красная последовательность сходится, так же как и синяя последовательность.

Ниже приведено доказательство правильности первоначального теста отношения.

Предположим, что $L = lim n → ∞ | а п + 1 а п | < 1 {\displaystyle L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|<1}$ $L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{{n}}}}\right|<1$ . Затем мы можем показать, что ряд абсолютно сходится, показав, что его члены в конечном итоге станут меньше, чем члены определенного сходящегося геометрического ряда. Для этого пусть $r = L + 1 2 {\ displaystyle r = {\ frac {L + 1} {2}}}$ $r = \frac{L+1}{2}$ . Тогда r строго между L и 1, и $| а п + 1 | < r | a n | {\displaystyle |a_{n+1}|$ $|a_{n+1}| <r |a_{n}|$ для достаточно большого n; скажем, для всех n больше N. Следовательно, $| а п + я | < r i | a n | {\displaystyle |a_{n+i}|$ $|a_{n+i}| <r^i|a_{n}|$ для каждого n>N и i>0, поэтому

∑ i = N + 1 ∞ | а я | = ∑ i = 1 ∞ | а N + я | < ∑ i = 1 ∞ r i | a N | = | a N | ∑ i = 1 ∞ r i = | a N | r 1 − r < ∞. {\displaystyle \sum _{i=N+1}^{\infty }|a_{i}|=\sum _{i=1}^{\infty }\left|a_{N+i}\right|<\sum _{i=1}^{\infty }r^{i}|a_{N}|=|a_{N}|\sum _{i=1}^{\infty }r^{i}=|a_{N}|{\frac {r}{1-r}}<\infty.}

\sum _{i=N+1}^{\infty }|a_{i}|=\sum _{i=1}^{\infty }\left|a_{N+i}\right|<\sum _{i=1}^{\infty }r^{i}|a_{N}|=|a_{N}|\sum _{i=1}^{\infty }r^{i}=|a_{N}|{\frac {r}{1-r}}<\infty.

То есть ряд абсолютно сходится.

С другой стороны, если L>1, то $| а п + 1 |>| а п | {\ displaystyle | a_ {n + 1} |>| a_ {n} |}$ $|a_{n+1}|>| a_ {n} |$ для достаточно большого n, так что предел слагаемых отличен от нуля. Следовательно, ряд расходится.

Расширения для L = 1

Как видно из предыдущего примера, тест отношения может быть неубедительным, если предел отношения равен 1. Однако расширения теста отношения иногда позволяют иметь дело с этим случаем.

Во всех приведенных ниже тестах предполагается, что Σa n представляет собой сумму с положительным a n. Эти тесты также могут применяться к любой серии с конечным числом отрицательные термины. Любой такой ряд можно записать как:

∑ n = 1 ∞ an = ∑ n = 1 N an + ∑ n = N + 1 ∞ an {\ displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n} = \ sum _ {n = 1} ^ {N} a_ {n} + \ sum _ {n = N + 1} ^ {\ infty} a_ {n}}

{\ displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n} = \ sum _ {n = 1} ^ {N} a_ {n} + \ sum _ { п = N + 1} ^ {\ infty} a_ {n}}

где a N - отрицательный член с наивысшим индексом. Первое выражение справа - это частичное s um, который будет конечным, и, таким образом, сходимость всего ряда будет определяться свойствами сходимости второго выражения справа, которое может быть переиндексировано для формирования серии всех положительных членов, начинающихся с n = 1.

Каждый тест определяет тестовый параметр (ρ n), который определяет поведение этого параметра, необходимое для установления сходимости или расхождения. Для каждого теста существует более слабая форма теста, которая вместо этого накладывает ограничения на lim n->∞ ρn.

. Все тесты имеют области, в которых они не могут описать свойства сходимости ∑a n. Фактически, никакой тест сходимости не может полностью описать свойства сходимости ряда. Это связано с тем, что если ∑a n сходится, может быть найден второй сходящийся ряд ∑b n, который сходится медленнее: т. Е. Он имеет свойство lim n->∞ (bn/an) = ∞. Кроме того, если ∑a n расходится, может быть найден второй расходящийся ряд ∞ (bn/an) = 0. Тесты сходимости по существу используют сравнительный тест на некотором конкретном семействе n и терпят неудачу для последовательностей, которые сходятся или расходятся медленнее.

Иерархия Де Моргана

Огастес Де Морган предложил иерархию тестов отношения типа

Параметры теста отношения ( $ρ n {\ displaystyle \ rho _ {n }}$ $\rho_n$ ) все нижеприведенные обычно включают термины формы $D nan / an + 1 - D n + 1 {\ displaystyle D_ {n} a_ {n} / a_ {n + 1} - D_ {n + 1}}$ $D_{n}a_{n}/a_{n+1}-D_{n+1}$ . Этот член можно умножить на $an + 1 / an {\ displaystyle a_ {n + 1} / a_ {n}}$ $a_{n+1}/a_n$ , чтобы получить $D n - D n + 1 an + 1 / ан {\ displaystyle D_ {n} -D_ {n + 1} a_ {n + 1} / a_ {n}}$ $D_{n}-D_{n+1}a_{n+1}/a_{n}$ . Этот термин может заменить прежний термин в определении параметров испытаний, и сделанные выводы останутся прежними. Соответственно, не будет никаких различий между ссылками, которые используют ту или иную форму параметра теста.
1. Тест отношения Д'Аламбера
Первый тест в иерархии Де Моргана - это тест отношения, описанный выше.
2. Тест Раабе
Это расширение принадлежит Джозефу Людвигу Раабе. Определите:
$ρ N ≡ N (anan + 1-1) {\ displaystyle \ rho _ {n} \ Equiv n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right)}$ $\rho _{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$
(и некоторые дополнительные термины, см. Али, Блэкберн, Фелд, Дурис (нет), Дурис2)

Ряд будет:
сойтись, если существует ac>1 такое, что $ρ n ≥ c {\ displaystyle \ rho _ {n} \ geq c}$ ${\ displaystyle \ rho _ {n} \ geq c}$ для всех n>N.
расходится, когда $ρ n ≤ 1 {\ displaystyle \ rho _ {n} \ leq 1}$ $\rho _{n}\leq 1$ для всех n>N.
В противном случае тест будет безрезультатным.
Для предельной версии серия будет:
Сходимся, если $ρ = lim n → ∞ ρ n>1 {\ displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}>1}$ $\rho =\lim _{n\to \infty }\rho _{n}>1$ (включая случай ρ = ∞)
Отклонение, если $lim n → ∞ ρ n < 1 {\displaystyle \lim _{n\to \infty }\rho _{n}<1}$ $\lim _{n\to \infty }\rho _{n}<1$ .
Если ρ = 1, проверка не дает результатов.
Если вышеуказанный предел не существует, возможно использование верхних и нижних пределов. В серии будут:
Конв. erge, если $lim inf n → ∞ ρ n>1 {\ displaystyle \ liminf _ {n \ to \ infty} \ rho _ {n}>1}$ $\liminf _{n\to \infty }\rho _{n}>1$
Diverge if lim sup ∞ ρ n < 1 {\displaystyle \limsup _{n\rightarrow \infty }\rho _{n}<1} $\limsup _{n\rightarrow \infty }\rho _{n}<1$
В противном случае тест не дает результатов.
Доказательство теста Раабе
Определение $ρ n ≡ n (anan + 1 - 1) {\ displaystyle \ rho _ {n} \ Equiv n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right)}$ $\rho _{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$ , нам не нужно предполагать, что предел существует; если $lim sup ρ n < 1 {\displaystyle \limsup \rho _{n}<1}$ $\limsup \rho _{n}<1$ , то $∑ an {\ displaystyle \ sum a_ {n}}$ $\sum a_{n}$ расходится, а если $lim inf ρ n>1 {\ displaystyle \ liminf \ rho _ {n}>1}$ $\liminf \rho _{n}>1$ сумма сходится.

Доказательство основывается на сравнении с $∑ 1 / n R {\ displaystyle \ sum 1 / n ^ {R}}$ ${\ displaystyle \ sum 1 / n ^ {R}}$ . Предположим сначала, что $lim sup ρ n < 1 {\displaystyle \limsup \rho _{n}<1}$ $\limsup \rho _{n}<1$ . Конечно, если $lim sup ρ n < 0 {\displaystyle \limsup \rho _{n}<0}$ $\limsup \rho _{n}<0$ , то $an + 1 ≥ an {\ displaystyle a_ {n + 1} \ geq a_ {n}}$ ${\ displaystyle a_ {n + 1} \ geq a_ {n}}$ для больших $n {\ displaystyle n}$ $n$ , поэтому сумма расходится; тогда предположим, что $0 ≤ lim sup ρ n < 1 {\displaystyle 0\leq \limsup \rho _{n}<1}$ $0\leq \limsup \rho _{n}<1$ . Существует $R < 1 {\displaystyle R<1}$ $R<1$ такой, что $ρ n ≤ R {\ displaystyle \ rho _ {n} \ leq R}$ $\rho _{n}\leq R$ для всех $n ≥ N {\ displaystyle n \ geq N }$ $n\geq N$ , то есть $an / an + 1 ≤ (1 + R n) ≤ e R / n {\ displaystyle a_ {n} / a_ {n + 1} \ leq \ left (1 + {\ frac {R} {n}} \ right) \ leq e ^ {R / n}}$ $a_{n}/a_{n+1}\leq \left(1+{\frac {R}{n}}\right)\leq e^{R/n}$ . Таким образом $an + 1 ≥ ane - R / n {\ displaystyle a_ {n + 1} \ geq a_ {n} e ^ {- R / n}}$ $a_{n+1}\geq a_{n}e^{-R/n}$ , что означает, что $an + 1 ≥ a N e - R (1 / N + ⋯ + 1 / n) ≥ ca N e - R log ⁡ (n) = ca N / n R {\ displaystyle a_ {n + 1} \ geq a_ {N } e ^ {- R (1 / N + \ dots + 1 / n)} \ geq ca_ {N} e ^ {- R \ log (n)} = ca_ {N} / n ^ {R}}$ $a_{n+1}\geq a_{N}e^{-R(1/N+\dots +1/n)}\geq ca_{N}e^{-R\log(n)}=ca_{N}/n^{R}$ для $n ≥ N {\ displaystyle n \ geq N}$ $n\geq N$ ; поскольку $R < 1 {\displaystyle R<1}$ $R<1$ это показывает, что $∑ a n {\ displaystyle \ sum a_ {n}}$ $\sum a_{n}$ расходится.

Доказательство второй половины полностью аналогично, с большинством неравенств просто обратным. Нам нужно предварительное неравенство для использования вместо простого $1 + t < e t {\displaystyle 1+t$ $1+t<e^{t}$ , которое использовалось выше: Исправьте $R {\ displaystyle R}$ $R$ и $N {\ Displaystyle N}$ $N$ . Обратите внимание, что $журнал ⁡ (1 + R n) = R n + O (1 n 2) {\ displaystyle \ log \ left (1 + {\ frac {R} {n}} \ right) = {\ frac {R} {n}} + O \ left ({\ frac {1} {n ^ {2}}} \ right)}$ $\log \left(1+{\frac {R}{n}}\right)={\frac {R}{n}}+O\left({\frac {1}{n^{2}}}\right)$ . Итак, $журнал ⁡ ((1 + RN)… (1 + R n)) = R (1 N + ⋯ + 1 n) + O (1) = R log ⁡ (n) + O (1) {\ displaystyle \ log \ left (\ left (1 + {\ frac {R} {N}} \ right) \ dots \ left (1 + {\ frac {R} {n}} \ right) \ right) = R \ left ({\ frac {1} {N}} + \ dots + {\ frac {1} {n}} \ right) + O (1) = R \ log (n) + O (1)}$ $\log \left(\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\right)=R\left({\frac {1}{N}}+\dots +{\frac {1}{n}}\right)+O(1)=R\log(n)+O(1)$ ; следовательно, $(1 + RN)… (1 + R n) ≥ cn R {\ displaystyle \ left (1 + {\ frac {R} {N}} \ right) \ dots \ left (1 + {\ frac {R} {n}} \ right) \ geq cn ^ {R}}$ $\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\geq cn^{R}$ .

Предположим теперь, что $lim inf ρ n>1 {\ displaystyle \ liminf \ rho _ {n}>1}$ $\liminf \rho _{n}>1$ . Аргументы как в в первом абзаце, используя неравенство, установленное в предыдущем абзаце, мы видим, что существует $R>1 {\ displaystyle R>1}$ $R>1$ таким образом, что $an + 1 ≤ ca N n - R {\ displaystyle a_ {n + 1} \ leq ca_ {N} n ^ {- R}}$ $a_{n+1}\leq ca_{N}n^{-R}$ для $n ≥ N {\ displaystyle n \ geq N}$ $n\geq N$ ; поскольку $R>1 {\ displaystyle R>1}$ $R>1$ это показывает, что $∑ {\ displaystyle \ sum a_ {n}}$ $\sum a_{n}$ сходится.
3. Тест Бертрана
Это расширение связано с Джозефом Бертраном и Огастесом Де Морганом.

Определение:
$ρ n ≡ n ln ⁡ n (anan + 1 - 1) - ln ⁡ n {\ displaystyle \ rho _ {n} \ Equiv n \ ln n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ ln n}$ $\rho _{n}\equiv n\ln n\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln n$
Бертрана test утверждает, что ряд будет:
сойтись, если существует ac>1, такое что $ρ n ≥ c {\ displaystyle \ rho _ {n} \ geq c}$ ${\ displaystyle \ rho _ {n} \ geq c}$ для всех n>N.
Расхождение, когда $ρ n ≤ 1 {\ displaystyle \ rho _ {n} \ leq 1}$ $\rho _{n}\leq 1$ для всех n>N.
В противном случае тест не дает результатов.
Для предельной версии ряд будет:
сойтись, если $ρ = lim n → ∞ ρ n>1 {\ displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}>1}$ $\rho =\lim _{n\to \infty }\rho _{n}>1$ (включая случай ρ = ∞)
Отклонение, если $lim n → ∞ ρ n < 1 {\displaystyle \lim _{n\to \infty }\rho _{n}<1}$ $\lim _{n\to \infty }\rho _{n}<1$ .
Если ρ = 1, проверка неубедительна.
Если вышеуказанный предел не существует, можно использовать верхний и нижний пределы. Ряд будет:
сходимся, если $lim inf ρ n>1 {\ displaystyle \ liminf \ rho _ {n}>1}$ $\liminf \rho _{n}>1$
Diverge if $lim sup ρ n < 1 {\displaystyle \limsup \rho _{n}<1}$ $\limsup \rho _{n}<1$
, тест не дает результатов.
4. Расширенный тест Бертрана
Это расширение, вероятно, впервые появилось у Маргарет Мартин. Краткое доказательство, основанное на тесте Куммера и без технических предположений (таких как существование пределы, например).

Пусть $K ≥ 1 {\ displaystyle K \ geq 1}$ $K\geq 1$ целое число, и пусть $ln (K) ⁡ (x) {\ displaystyle \ ln _ {(K)} (x)}$ $\ln _{(K)}(x)$ обозначает $K {\ displaystyle K}$ $K$ th итерацию из натуральный логарифм, т. Е. $ln (1) ⁡ (x) = ln ⁡ (x) {\ displaystyle \ ln _ {(1)} (x) = \ ln (x)}$ $\ln _{(1)}(x)=\ln(x)$ и для любого $2 ≤ k ≤ K {\ displaystyle 2 \ leq k \ leq K}$ $2\leq k\leq K$ , $ln (k) ⁡ (x) = ln (k - 1) ⁡ (пер ⁡ (x)) {\ displaystyle \ ln _ {(k)} (x) = \ ln _ {(k-1)} (\ ln (x))}$ $\ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))$ .

Предположим, что соотношение $an / an + 1 {\ displaystyle a_ {n} / a_ {n + 1}}$ $a_{n}/a_{n+1}$ , когда $n {\ displaystyle n}$ $n$ большой, может быть представлен в виде
$anan + 1 = 1 + 1 n + 1 n ∑ i = 1 K - 1 1 ∏ k = 1 i ln (k) ⁡ (n) + ρ nn ∏ k = 1 K ln (k) ⁡ (N), К ≥ 1. {\ Displaystyle {\ frac {a_ {n}} {a_ {n + 1}}} = 1 + {\ frac {1} {n}} + {\ frac {1 } {n}} \ sum _ {i = 1} ^ {K-1} {\ frac {1} {\ prod _ {k = 1} ^ {i} \ ln _ {(k)} (n)} } + {\ frac {\ rho _ {n}} {n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n)}}, \ quad K \ geq 1.}$ ${\frac {a_{n}}{a_{n+1}}}=1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho _{n}}{n\prod _{k=1}^{K}\ln _{(k)}(n)}},\quad K\geq 1.$
(Предполагается, что пустая сумма равна 0. При $K = 1 {\ displaystyle K = 1}$ $K=1$ тест сводится к тесту Бертрана.)

. Значение $ρ n {\ displaystyle \ rho _ {n}}$ $\rho _{n}$ можно явно представить в виде
$ρ n = n ∏ k = 1 K ln (k) ⁡ (n) (anan + 1 - 1) - j знак равно 1 K ∏ k = 1 j ln (K - k + 1) ⁡ (n). {\ displaystyle \ rho _ {n} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) \ left ({\ frac {a_ {n}} {a_ {n) +1}}} - 1 \ right) - \ sum _ {j = 1} ^ {K} \ prod _ {k = 1} ^ {j} \ ln _ {(K-k + 1)} (n).}$ $\rho _{n}=n\prod _{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum _{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n).$
Расширенный тест Бертрана утверждает, что ряд
Сходится, когда существует $c>1 {\ displaystyle c>1}$ $c>1$ таким образом, что $ρ n ≥ c {\ displaystyle \ rho _ {n} geq c}$ ${\ displaystyle \ rho _ {n} \ geq c}$ для всех $n>N {\ displaystyle n>N}$ $n>N$ .
Отклонение, когда $ρ n ≤ 1 {\ displaystyle \ rho _ {n} \ leq 1 }$ $\rho _{n}\leq 1$ для всех $n>N {\ displaystyle n>N}$ $n>N$ .
В противном случае тест не дает результатов. 651>Для предельной версии ряд
сходится, если $ρ = lim n → ∞ ρ n>1 {\ displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}>1}$ $\rho =\lim _{n\to \infty }\rho _{n}>1$ (это включает случай $ρ = ∞ {\ displaystyle \ rho = \ infty}$ $\rho =\infty$ )
Diverge if $lim n → ∞ ρ n < 1 {\displaystyle \lim _{n\to \infty }\rho _{n}<1}$ $\lim _{n\to \infty }\rho _{n}<1$ .
If $ρ = 1 {\ displaystyle \ rho = 1}$ $\rho =1$ , проверка не дает результатов.
Если вышеуказанный предел не существует, можно использовать верхний и нижний пределы. Ряд
сходится, если $lim inf ρ n>1 {\ displaystyle \ liminf \ rho _ {n}>1}$ $\liminf \rho _{n}>1$
Diverge if $lim sup ρ n < 1 {\displaystyle \limsup \rho _{n}<1}$ $\limsup \rho _{n}<1$
В противном случае
Для применения расширенного теста Бертрана см. Процесс рождения-смерти.
5. Тест Гаусса
Это расширение связано с Карлом Фридрихом Гауссом.

Предполагая n>0 и r>1, если ограниченная последовательность C n может быть найдена так, что для всех n:
$anan + 1 = 1 + ρ n + C nnr { \ Displaystyle {\ frac {a_ {n}} {a_ {n + 1}}} = 1 + {\ frac {\ rho} {n}} + {\ frac {C_ {n}} {n ^ {r} }}}$ ${\frac {a_{n}}{a_{n+1}}}=1+{\frac {\rho }{n}}+{\frac {C_{n}}{n^{r}}}$
тогда ряд будет:
Сходимся, если $ρ>1 {\ displaystyle \ rho>1}$ $\rho>1$
Дивергент, если $ρ ≤ 1 {\ displaystyle 1 \ rho }$ $\rho \leq 1$
6. Тест Куммера
Это расширение связано с Эрнстом Куммером.

. Пусть ζ n - вспомогательная последовательность положительных констант. Определите
$ρ N ≡ (ζ nanan + 1 - ζ n + 1) {\ displaystyle \ rho _ {n} \ Equiv \ left (\ zeta _ {n} {\ frac {a_ {n}} {a_ { n + 1}}} - \ zeta _ {n + 1} \ right)}$ $\rho _{n}\equiv \left(\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}\right)$
Тест Куммера утверждает, что ряд будет:
сходиться, если существует $c>0 {\ displaystyle c>0 }$ $c>0$ такие что $ρ n ≥ c {\ displaystyle \ rho _ {n} \ geq c}$ ${\ displaystyle \ rho _ {n} \ geq c}$ для всех n>N. (Обратите внимание, что это не то же самое, что сказать $ρ n>0 { \ displaystyle \ rho _ {n}>0}$ $\rho _{n}>0$ )
Отклонить, если $ρ n ≤ 0 {\ displaystyle \ rho _ {n} \ leq 0}$ $\rho _{n}\leq 0$ для всех n>N и $∑ N = 1 ∞ 1 / ζ n {\ displaystyle \ sum _ {n = 1} ^ {\ infty} 1 / \ zeta _ {n}}$ $\sum _{n=1}^{\infty }1/\zeta _{n}$ расходится.
Для в предельной версии ряд будет:
сойтись, если $lim n → ∞ ρ n>0 {\ displaystyle \ lim _ {n \ to \ infty} \ rho _ {n}>0}$ $\lim _{n\to \infty }\rho _{n}>0$ (включая случай ρ = ∞)
Отклонение, если $lim n → ∞ ρ n < 0 {\displaystyle \lim _{n\to \infty }\rho _{n}<0}$ $\lim _{n\to \infty }\rho _{n}<0$ и $lim n → ∞ ρ n < 0 {\displaystyle \lim _{n\to \infty }\rho _{n}<0}$ $\lim _{n\to \infty }\rho _{n}<0$ >∑ N = 1 ∞ 1 / ζ n {\ displaystyle \ sum _ {n = 1} ^ {\ infty} 1 / \ zeta _ {n}} $\sum _{n=1}^{\infty }1/\zeta _{n}$ расходится.
В противном случае тест не дает результатов
Если вышеуказанный предел не существует, можно использовать верхний и нижний пределы. Ряд будет
сходиться, если $lim inf n → ∞ ρ n>0 {\ displaystyle \ liminf _ {n \ to \ infty} \ rho _ {n}>0}$ $\liminf _{n\to \infty }\rho _{n}>0$
Diverge 283>lim sup n → ∞ ρ n < 0 {\displaystyle \limsup _{n\to \infty }\rho _{n}<0} $\limsup _{n\to \infty }\rho _{n}<0$ и $∑ 1 / ζ n {\ displaystyle \ sum 1 / \ zeta _ {n}}$ $\sum 1/\zeta _{n}$ расходится.
Особые случаи
Все тесты в иерархии Де Моргана, кроме теста Гаусса, можно легко рассматривать как частные случаи теста Куммера:
Для теста отношения пусть ζ n = 1. Тогда:
$ρ К уммер = (анан + 1 - 1) = 1 / ρ R atio - 1 {\ displaystyle \ rho _ {Kummer} = \ left ({\ frac {a_ {n}} {a_ {n + 1}}) } -1 \ right) = 1 / \ rho _ {Ratio} -1}$ $\rho _{Kummer}=\left({\frac {a_{n}}{a_{n+1}}}-1\right)=1/\rho _{Ratio}-1$
Для теста Раабе пусть ζ n = n. Тогда:
$ρ K ummer = (nanan + 1 - (n + 1)) = ρ R aabe - 1 {\ displaystyle \ rho _ {Kummer} = \ left (n {\ frac {a_ {n}} {a_ {n + 1}}}} - (n + 1) \ right) = \ rho _ {Raabe} -1}$ $\rho _{Kummer}=\left(n{\frac {a_{n}}{a_{n+1}}}-(n+1)\right)=\rho _{Raabe}-1$
Для теста Бертрана пусть ζ n = n ln (n). Тогда:
$ρ К уммер знак равно N пер ⁡ (п) (анан + 1) - (п + 1) пер ⁡ (п + 1) {\ displaystyle \ rho _ {Kummer} = п \ пер (п) \ влево ( {\ frac {a_ {n}} {a_ {n + 1}}} \ right) - (n + 1) \ ln (n + 1)}$ $\rho _{Kummer}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}\right)-(n+1)\ln(n+1)$
Использование $ln ⁡ (n + 1) = пер ⁡ (п) + пер ⁡ (1 + 1 / п) {\ Displaystyle \ пер (п + 1) = \ пер (п) + \ пер (1 + 1 / п)}$ ${\ displaystyle \ ln (n + 1) = \ ln (n) + \ ln (1 + 1 / n)}$ и аппроксимация $ln ⁡ (1 + 1 / n) → 1 / n {\ displaystyle \ ln (1 + 1 / n) \ rightarrow 1 / n}$ $\ln(1+1/n)\rightarrow 1/n$ для большого n, что незначительно по сравнению с другими терминами, $ρ K ummer {\ displaystyle \ rho _ {Kummer}}$ $\rho _{Kummer}$ может быть записано:
$ρ K ummer = n ln ⁡ (n) (anan + 1 - 1) - пер ⁡ (N) - 1 = ρ B ertrand - 1 {\ displaystyle \ rho _ {Kummer} = n \ ln (n) \ left ({\ frac {a_ {n}} {a_ { n + 1}}} - 1 \ right) - \ ln (n) -1 = \ rho _ {Bertrand} -1}$ $\rho _{Kummer}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln(n)-1=\rho _{Bertrand}-1$
Для расширенного теста Бертрана, пусть $ζ n = n ∏ k = 1 K ln (k) ⁡ (n). {\ displaystyle \ zeta _ {n} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n).}$ $\zeta _{n}=n\prod _{k=1}^{K}\ln _{(k)}(n).$ Из серии Тейлора расширение для большого $n {\ displaystyle n}$ $n$ мы приходим к приближению
$ln (k) ⁡ (n + 1) = ln (k) ⁡ (n) + 1 N ∏ J знак равно 1 К - 1 пер (J) ⁡ (п) + О (1 N 2), {\ Displaystyle \ пер _ {(к)} (п + 1) = \ пер _ {(к) } (n) + {\ frac {1} {n \ prod _ {j = 1} ^ {k-1} \ ln _ {(j)} (n)}} + O \ left ({\ frac {1 } {n ^ {2}}} \ right),}$ $\ln _{(k)}(n+1)=\ln _{(k)}(n)+{\frac {1}{n\prod _{j=1}^{k-1}\ln _{(j)}(n)}}+O\left({\frac {1}{n^{2}}}\right),$
где пустое произведение предполагается равным 1. Тогда
$ρ K ummer = n ∏ k = 1 K ln (k) ⁡ (n) anan + 1 - (n + 1) [∏ k = 1 K (ln (k) ⁡ (n) + 1 n ∏ j = 1 k - 1 ln (j) ⁡ (n))] + o (1) = n ∏ k = 1 K ln (k) ⁡ (n) (anan + 1 - 1) - ∑ j = 1 K ∏ k = 1 j ln (K - k + 1) ⁡ (n) - 1 + o (1). {\ displaystyle \ rho _ {Kummer} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) {\ frac {a_ {n}} {a_ {n + 1} }} - (n + 1) \ left [\ prod _ {k = 1} ^ {K} \ left (\ ln _ {(k)} (n) + {\ frac {1} {n \ prod _ { j = 1} ^ {k-1} \ ln _ {(j)} (n)}} \ right) \ right] + o (1) = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ sum _ {j = 1} ^ {K} \ prod _ {k = 1} ^ {j} \ ln _ {(K-k + 1)} (n) -1 + o (1).}$ $\rho _{Kummer}=n\prod _{k=1}^{K}\ln _{(k)}(n){\frac {a_{n}}{a_{n+1}}}-(n+1)\left[\prod _{k=1}^{K}\left(\ln _{(k)}(n)+{\frac {1}{n\prod _{j=1}^{k-1}\ln _{(j)}(n)}}\right)\right]+o(1)=n\prod _{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum _{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n)-1+o(1).$
Следовательно,
$ρ K ummer = ρ E xtended B ertrand - 1. {\ displaystyle \ rho _ {Kummer} = \ rho _ {ExtendedBertrand} -1.}$ $\rho _{Kummer}=\rho _{ExtendedBertrand}-1.$
Обратите внимание, что для этих четырех тестов, чем выше они находятся в иерархии Де Моргана, тем медленнее $1 / ζ n {\ displaystyle 1 / \ zeta _ {n}}$ $1/\zeta _{n}$ ряд расходится.
Доказательство теста Куммера
Если $ρ n>0 {\ displaystyle \ rho _ {n}>0}$ $\rho _{n}>0$ затем зафиксируйте положительное число $0 < δ < ρ n {\displaystyle 0<\delta <\rho _{n}}$ $0<\delta <\rho _{n}$ . Существует натуральное число $N {\ displaystyle N}$ $N$ так, что для каждого $n>N, {\ displaystyle n>N,}$ $n>N,$
$δ ≤ ζ нанан + 1 - ζ n + 1. {\ displaystyle \ delta \ leq \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1}.}$ $\delta\leq\zeta_{n}\frac{a_{n}}{a_{n+1}}-\zeta_{n+1}.$
Начиная с $, + 1>0 {\ displaystyle a_ {n + 1}>0}$ $a_{n+1}>0$ , для каждого $n>N, {\ displaystyle n>N,}$ $n>N,$
$0 ≤ δ an + 1 ≤ ζ nan - ζ n + 1 an + 1. {\ displaystyle 0 \ leq \ delta a_ {n + 1} \ leq \ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1}.}$ $0\leq \delta a_{n+1}\leq \zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}.$
В частности, $ζ n + 1 an + 1 ≤ ζ nan {\ displaystyle \ zeta _ {n + 1} a_ {n + 1} \ leq \ zeta _ {n} a_ {n}}$ $\zeta_{n+1}a_{n+1}\leq \zeta_{n}a_{n}$ для всех $n ≥ N {\ displaystyle n \ geq N}$ $n\geq N$ , что означает, что начиная с индекса $N {\ displaystyle N}$ $N$ последовательность $ζ nan>0 {\ displaystyle \ zeta _ {n} a_ {n}>0}$ $\zeta_{n}a_{n}>0$ монотонно убывает и положительно, что, в частности, означает, что он ограничен снизу нулем. Следовательно, предел
$lim n → ∞ ζ nan = L {\ displaystyle \ lim _ {n \ to \ infty} \ zeta _ {n} a_ {n} = L}$ $\lim_{n\to\infty}\zeta_{n}a_{n}=L$ существует.
Это означает, что положительная телескопическая серия
$∑ n = 1 ∞ (ζ нан - ζ N + 1 ан + 1) {\ displaystyle \ sum _ {n = 1} ^ {\ infty} \ left (\ zeta _ {n} a_ {n} - \ zeta _ {n + 1 } a_ {n + 1} \ right)}$ $\sum_{n=1}^{\infty}\left(\zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}\right)$ сходится,
и поскольку для всех $n>N, {\ displaystyle n>N,}$ $n>N,$
$δ an + 1 ≤ ζ nan - ζ n + 1 an + 1 {\ displaystyle \ delta a_ {n + 1} \ leq \ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1}}$ $\delta a_{n+1}\leq \zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}$
по тесту прямого сравнения для положительных серий, серия $∑ n = 1 ∞ δ an + 1 {\ displaystyle \ sum _ {n = 1} ^ {\ infty} \ delta a_ {n + 1}}$ $\sum_{n=1}^{\infty}\delta a_{n+1}$ сходится.

С другой стороны, если $ρ < 0 {\displaystyle \rho <0}$ $\rho<0$ , то существует такое N, что $ζ nan {\ displaystyle \ zeta _ {n} a_ {n}}$ $\zeta_n a_n$ увеличивается для $n>N {\ displaystyle n>N}$ $n>N$ . В частности, существует $ϵ>0 {\ displaystyle \ epsilon>0}$ $\epsilon>0$ , для которого $ζ nan>ϵ {\ displaystyle \ zeta _ {n} a_ {n}>\ epsilon}$ $\zeta_n a_n>\ epsilon$ для всех $n>N {\ displaystyle n>N}$ $n>N$ и т. д. $∑ nan Знак равно ∑ нан ζ N ζ N {\ displaystyle \ sum _ {n} a_ {n} = \ sum _ {n} {\ frac {a_ {n} \ zeta _ {n}} {\ zeta _ {n}} }}$ $\sum_n a_n=\sum_n \frac{a_n\zeta_n}{\zeta_n}$ расходится по сравнению с $∑ n ϵ ζ n {\ displaystyle \ sum _ {n} {\ frac {\ epsilon} {\ zeta _ {n}}}}$ $\sum_n \frac \epsilon {\zeta_n}$ .
Second Тест отношения
Более точный тест отношения - второй тест отношения: для $an>0 {\ displaystyle a_ {n}>0}$ $a_{n}>0$ define:
$L 0 ≡ lim n → ∞ a 2 nan { \ Displaystyle L_ {0} \ Equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$ $L_{0}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$
$L 1 ≡ lim n → ∞ a 2 n + 1 an {\ displaystyle L_ {1} \ Equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$ $L_{1}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$L ≡ max (L 0, L 1) {\ displaystyle L \ Equiv \ max (L_ {0}, L_ {1})}$ $L\equiv \max(L_{0},L_{1})$
По второму тесту на соотношение ряд будет:
сойтись, если $L < 1 2 {\displaystyle L<{\frac {1}{2}}}$ $L<{\frac {1}{2}}$
расходиться, если $L>1 2 {\ displaystyle L>{\ frac {1} {2}}}$ $L>{\ frac {1} {2}}$
Если $L = 1 2 {\ displaystyle L = {\ frac {1} {2}}}$ $L={\frac {1}{2}}$ , тогда проверка не дает результатов.
Если вышеуказанные пределы не существуют, возможно, можно использовать верхние и нижние пределы. Определите:
$L 0 ≡ lim sup n → ∞ a 2 nan {\ displaystyle L_ {0} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}} }}$ $L_{0}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$ $L 1 ≡ lim sup n → ∞ a 2 n + 1 an {\ displaystyle L_ {1} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} { a_ {n}}}}$ $L_{1}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$ℓ 0 ≡ lim inf n → ∞ a 2 nan {\ displaystyle \ ell _ {0} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n} } {a_ {n}}}}$ $\ell _{0}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$ $ℓ 1 ≡ lim inf n → ∞ a 2 n + 1 an {\ displaystyle \ ell _ {1} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$ ${\ displaystyle \ ell _ {1} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n +1}} {a_ {n}}}}$
$L ≡ макс (L 0, L 1) {\ displaystyle L \ Equiv \ max (L_ {0}, L_ {1})}$ $L\equiv \max(L_{0},L_{1})$ $ℓ ≡ min (ℓ 0, ℓ 1) {\ displaystyle \ ell \ Equiv \ min (\ ell _ {0}, \ ell _ {1})}$ $\ell \equiv \min(\ell _{0},\ell _{1})$
Тогда ряд будет:
сойтись, если $L < 1 2 {\displaystyle L<{\frac {1}{2}}}$ $L<{\frac {1}{2}}$
Отклонить, если $ℓ>1 2 {\ displaystyle \ ell>{\ frac {1} {2}}}$ $\ell>{\ frac {1} {2}}$
Если $ℓ ≤ 1 2 ≤ L {\ displaystyle \ ell \ leq {\ frac {1} {2}} \ l eq L}$ $\ell \leq {\frac {1}{2}}\leq L$ , тогда тест не дает результатов.
$m {\ displaystyle m}$ $m$ Тест с отношением th
Этот тест является прямым продолжением теста второго отношения. Для $0 ≤ k ≤ m - 1, {\ displaystyle 0 \ leq k \ leq m-1,}$ $0\leq k\leq m-1,$ и положительного $an {\ displaystyle a_ {n}}$ $a_{n}$ определить:
$L К ≡ lim n → ∞ amn + kan {\ displaystyle L_ {k} \ Equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ { n}}}}$ $L_{k}\equiv \lim _{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}$
$L ≡ макс (L 0, L 1,…, L m - 1) {\ displaystyle L \ Equiv \ max (L_ {0}, L_ {1}, \ ldots, L_ {m -1})}$ $L\equiv \max(L_{0},L_{1},\ldots,L_{m-1})$
По критерию $m {\ displaystyle m}$ $m$ th ratio test, ряд будет:
сходимся, если $L < 1 m {\displaystyle L<{\frac {1}{m}}}$ $L<{\frac {1}{m}}$
расходиться, если $L>1 m {\ displaystyle L>{\ frac {1} {m}}}$ $L>{\ frac {1} {m}}$
Если $L = 1 м {\ displaystyle L = {\ frac {1} { m}}}$ $L={\frac {1}{m}}$ , тогда тест не дает результатов.
Если вышеуказанные пределы не существуют, можно использовать верхние и нижние пределы. Для $0 ≤ k ≤ m - 1 {\ displaystyle 0 \ leq k \ leq m-1}$ $0\leq k\leq m-1$ определить:
$L k ≡ lim sup n → ∞ amn + kan {\ displaystyle L_ {k} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$ ${\ displaystyle L_ {k} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
$ℓ k ≡ lim inf n → ∞ amn + kan {\ displaystyle \ ell _ {k} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$ $\ell _{k}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}$
$L ≡ max (L 0, L 1,…, L м - 1) {\ Displaystyle L \ Equiv \ max (L_ {0}, L_ {1}, \ ldots, L_ {m-1})}$ $L\equiv \max(L_{0},L_{1},\ldots,L_{m-1})$ $ℓ ≡ мин (ℓ 0, ℓ 1,…, ℓ м - 1) {\ Displaystyle \ ell \ Equiv \ min (\ ell _ {0}, \ ell _ {1}, \ ldots, \ ell _ {m-1})}$ $\ell \equiv \min(\ell _{0},\ell _{1},\ldots,\ell _{m-1})$
Тогда серия будет:
сойтись, если $L < 1 m {\displaystyle L<{\frac {1}{m}}}$ $L<{\frac {1}{m}}$
расходиться, если $ℓ>1 m {\ displaystyle \ ell>{\ frac {1} {m}}}$ $\ell>{\ frac {1} { m}}$
Если $ℓ ≤ 1 m ≤ L {\ displaystyle \ ell \ leq {\ frac {1} {m}} \ leq L}$ $\ell \leq {\frac {1}{m}}\leq L$ , то проверка не дает результатов.
$φ { \ displaystyle \ varphi}$ $\varphi$ -ratio test
Этот тест является расширением $m {\ displaystyle m}$ $m$ -го теста отношения.

Предположим, что последовательность $a n {\ displaystyle a_ {n}}$ $a_{n}$ представляет собой положительную убывающую последовательность.

Пусть $φ: Z + → Z + {\ displaystyle \ varphi: \ mathbb {Z} ^ {+} \ to \ mathbb {Z} ^ {+}}$ $\varphi :\mathbb {Z} ^{+}\to \mathbb {Z} ^{+}$ быть таким, что $lim n → ∞ n φ (n) {\ displaystyle \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$ $\lim _{n\to \infty }{\frac {n}{\varphi (n)}}$ существует. Обозначим $α = lim n → ∞ n φ (n) {\ displaystyle \ alpha = \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$ $\alpha =\lim _{n\to \infty }{\frac {n}{\varphi (n)}}$ , и предположим $0 < α < 1 {\displaystyle 0<\alpha <1}$ $0<\alpha<1$ .

. Предположим также, что $lim n → ∞ a φ (n) an = L. {\ displaystyle \ lim _ {n \ to \ infty} {\ frac {a _ {\ varphi (n)}} {a_ {n}}} = L.}$ $\lim _{n\to \infty }{\frac {a_{\varphi (n)}}{a_{n}}}=L.$

Тогда ряд будет:
сойтись, если $L < α {\displaystyle L<\alpha }$ $L<\alpha$
Отклонить, если $ℓ>α {\ displaystyle \ ell>\ alpha}$ $\ell>\ alpha$
Если $L = α {\ displaystyle L = \ alpha}$ $L=\alpha$ , то
См. также
Корневой тест
Радиус сходимости
Сноски
Ссылки
d'Alembert, J. (1768), Opuscules, V, стр. 171–183.
Апостол, Том М. (1974), Математический анализ (2-е изд.), Аддисон-Уэсли, ISBN 978-0-201-00288-1 : §8.14.
Кнопп, Конрад (1956), Бесконечные последовательности и серии, Нью-Йорк: Dover Publications, Bibcode : 1956iss..book..... K, ISBN 978-0-486-60153-3 : §3.3, 5.4.
Рудин, Вальтер (1976), Принципы математического анализа (3-е изд.), Нью-Йорк: McGraw-Hill, Inc., ISBN 978-0-07-054235-8 : §3.34.
, Энциклопедия математики, EMS Press, 2001 [1994]
, Энциклопедия математики, EMS Press, 2001 [1994]
, Энциклопедия математики, EMS Press, 2001 [ 1994]
Уотсон, штат Джорджия; Whittaker, ET (1963), Курс современного анализа (4-е изд.), Cambridge University Press, ISBN 978-0-521-58807-2 : §2.36, 2.37.

$L 0 ≡ lim sup n → ∞ a 2 nan {\ displaystyle L_ {0} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}} }}$ $L_{0}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$		$L 1 ≡ lim sup n → ∞ a 2 n + 1 an {\ displaystyle L_ {1} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} { a_ {n}}}}$ $L_{1}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$ℓ 0 ≡ lim inf n → ∞ a 2 nan {\ displaystyle \ ell _ {0} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n} } {a_ {n}}}}$ $\ell _{0}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$		$ℓ 1 ≡ lim inf n → ∞ a 2 n + 1 an {\ displaystyle \ ell _ {1} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$ ${\ displaystyle \ ell _ {1} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n +1}} {a_ {n}}}}$
$L ≡ макс (L 0, L 1) {\ displaystyle L \ Equiv \ max (L_ {0}, L_ {1})}$ $L\equiv \max(L_{0},L_{1})$		$ℓ ≡ min (ℓ 0, ℓ 1) {\ displaystyle \ ell \ Equiv \ min (\ ell _ {0}, \ ell _ {1})}$ $\ell \equiv \min(\ell _{0},\ell _{1})$

$L k ≡ lim sup n → ∞ amn + kan {\ displaystyle L_ {k} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$ ${\ displaystyle L_ {k} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
$ℓ k ≡ lim inf n → ∞ amn + kan {\ displaystyle \ ell _ {k} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$ $\ell _{k}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}$
$L ≡ max (L 0, L 1,…, L м - 1) {\ Displaystyle L \ Equiv \ max (L_ {0}, L_ {1}, \ ldots, L_ {m-1})}$ $L\equiv \max(L_{0},L_{1},\ldots,L_{m-1})$		$ℓ ≡ мин (ℓ 0, ℓ 1,…, ℓ м - 1) {\ Displaystyle \ ell \ Equiv \ min (\ ell _ {0}, \ ell _ {1}, \ ldots, \ ell _ {m-1})}$ $\ell \equiv \min(\ell _{0},\ell _{1},\ldots,\ell _{m-1})$

Тест соотношения

сходятся, потому что L < 1

расходится, потому что L>1

Неубедительно, потому что L = 1

Иерархия Де Моргана

1. Тест отношения Д'Аламбера

2. Тест Раабе

Доказательство теста Раабе

3. Тест Бертрана

4. Расширенный тест Бертрана

5. Тест Гаусса

6. Тест Куммера

Особые случаи

Доказательство теста Куммера

Second Тест отношения

m {\ displaystyle m}Тест с отношением th

φ { \ displaystyle \ varphi}-ratio test

$m {\ displaystyle m}$ $m$ Тест с отношением th

$φ { \ displaystyle \ varphi}$ $\varphi$ -ratio test