Метод крутого спуска

Для алгоритма оптимизации см. Градиентный спуск.

В математике метод градиентного спуска или методом перевала является продолжением метода Лапласа для аппроксимации интеграла, где один деформируется интегральный контур в комплексной плоскости проходить вблизи стационарной точки ( седловой точки ), примерно в том направлении наискорейший спуск или стационарная фаза. Приближение перевала используется с интегралами в комплексной плоскости, тогда как метод Лапласа используется с вещественными интегралами.

Подлежащий оценке интеграл часто имеет вид

${\ Displaystyle \ int _ {C} е (г) е ^ {\ лямбда г (г)} \, дз,}$

где C - контур, а λ большое. Один из вариантов метода наискорейшего спуска деформирует контур интегрирования C в новый путь интегрирования C ' так, чтобы выполнялись следующие условия:

1. C ′ проходит через один или несколько нулей производной g ′ ( z),
2. мнимая часть g ( z) постоянна на C ′.

Метод наискорейшего спуска был впервые опубликован Дебаем (1909), который использовал его для оценки функций Бесселя и указал, что он имел место в неопубликованной заметке Римана (1863) о гипергеометрических функциях. Контур наискорейшего спуска обладает свойством минимаксности, см. Федорюк (2001). Сигель (1932) описал некоторые другие неопубликованные заметки Римана, в которых он использовал этот метод для вывода формулы Римана – Зигеля. ошибка harvtxt: нет цели: CITEREFFedoryuk2001 ( помощь )

• 1 Основная идея
• 2 Этимология
• 3 Простая оценка ^[2]
• 4 Случай единственной невырожденной седловой точки
  • 4.1 Основные понятия и обозначения
  • 4.2 Комплексная лемма Морса
  • 4.3. Асимптотическое разложение в случае одной невырожденной седловой точки.
• 5 Случай кратных невырожденных седловых точек
• 6 Другие случаи
• 7 Расширения и обобщения
• 8 См. Также
• 9 Примечания
• 10 Ссылки

Метод наискорейшего спуска - это метод аппроксимации комплексного интеграла вида

$${\ Displaystyle I (\ lambda) = \ int _ {C} f (z) e ^ {\ lambda g (z)} \, \ mathrm {d} z}$$ для больших, где и - аналитические функции от. Поскольку подынтегральное выражение является аналитическим, контур можно деформировать в новый контур без изменения интеграла. В частности, ищут новый контур, на котором мнимая часть постоянна. потом${\ displaystyle \ lambda \ rightarrow \ infty}$${\ displaystyle f (z)}$${\ displaystyle g (z)}$ ${\ displaystyle z}$${\ displaystyle C}$${\ displaystyle C '}$${\ displaystyle g (z) = {\ text {Re}} \ {g (z) \} + i \, {\ text {Im}} \ {g (z) \}}$ $${\ displaystyle I (\ lambda) = e ^ {i \ lambda {\ text {Im}} \ {g (z) \}} \ int _ {C '} f (z) e ^ {\ lambda {\ text {Re}} \ {g (z) \}} \, \ mathrm {d} z,}$$ а оставшийся интеграл можно аппроксимировать другими методами, например методом Лапласа.

Этот метод называется методом наискорейшего спуска, потому что для аналитических контуров с постоянной фазой они эквивалентны контурам наискорейшего спуска. ${\ displaystyle g (z)}$

Если -

аналитическая функция от, она удовлетворяет уравнениям Коши – Римана ${\ Displaystyle г (г) = Икс (г) + iY (г)}$ ${\ displaystyle z = x + iy}$ $${\ displaystyle {\ frac {\ partial X} {\ partial x}} = {\ frac {\ partial Y} {\ partial y}} \ qquad {\ text {and}} \ qquad {\ frac {\ partial X } {\ partial y}} = - {\ frac {\ partial Y} {\ partial x}}.}$$ потом $${\ displaystyle {\ frac {\ partial X} {\ partial x}} {\ frac {\ partial Y} {\ partial x}} + {\ frac {\ partial X} {\ partial y}} {\ frac { \ partial Y} {\ partial y}} = \ nabla X \ cdot \ nabla Y = 0,}$$ Таким образом, контуры постоянной фазы также являются контурами наискорейшего спуска.

Пусть f, S  : C ⁿ → C и C ⊂ C ⁿ. Если  

${\ Displaystyle М = \ sup _ {х \ в C} \ Re (S (x)) lt;\ infty,}$

где обозначает действительную часть, и существует положительное вещественное число λ 0 такое, что ${\ Displaystyle \ Re (\ cdot)}$

${\ displaystyle \ int _ {C} \ left | f (x) e ^ {\ lambda _ {0} S (x)} \ right | dx lt;\ infty,}$

то справедлива следующая оценка:

${\ displaystyle \ left | \ int _ {C} f (x) e ^ {\ lambda S (x)} dx \ right | \ leqslant {\ text {const}} \ cdot e ^ {\ lambda M}, \ qquad \ forall \ lambda \ in \ mathbb {R}, \ quad \ lambda \ geqslant \ lambda _ {0}.}.$

Доказательство простой оценки:

${\ Displaystyle {\ begin {align} \ left | \ int _ {C} f (x) e ^ {\ lambda S (x)} dx \ right | amp; \ leqslant \ int _ {C} | f (x) | \ left | e ^ {\ lambda S (x)} \ right | dx \\ amp; \ Equiv \ int _ {C} | f (x) | e ^ {\ lambda M} \ left | e ^ {\ lambda _ {0} (S (x) -M)} e ^ {(\ lambda - \ lambda _ {0}) (S (x) -M)} \ right | dx \\ amp; \ leqslant \ int _ {C } | f (x) | e ^ {\ lambda M} \ left | e ^ {\ lambda _ {0} (S (x) -M)} \ right | dx amp;amp; \ left | e ^ {(\ lambda - \ лямбда _ {0}) (S (x) -M)} \ right | \ leqslant 1 \\ amp; = \ underbrace {e ^ {- \ lambda _ {0} M} \ int _ {C} \ left | f (x) e ^ {\ lambda _ {0} S (x)} \ right | dx} _ {\ text {const}} \ cdot e ^ {\ lambda M}. \ end {выравнивается}}}$

Основные понятия и обозначения

Пусть x - комплексный n -мерный вектор и

${\ Displaystyle S '' _ {xx} (x) \ Equiv \ left ({\ frac {\ partial ^ {2} S (x)} {\ partial x_ {i} \ partial x_ {j}}} \ right), \ qquad 1 \ leqslant i, \, j \ leqslant n,}$

обозначают матрицу Гессе для функции S ( x). Если

${\ displaystyle {\ boldsymbol {\ varphi}} (x) = (\ varphi _ {1} (x), \ varphi _ {2} (x), \ ldots, \ varphi _ {k} (x))}$

является векторной функцией, то ее матрица Якоби определяется как

${\ displaystyle {\ boldsymbol {\ varphi}} _ {x} '(x) \ Equiv \ left ({\ frac {\ partial \ varphi _ {i} (x)} {\ partial x_ {j}}} \ справа), \ qquad 1 \ leqslant i \ leqslant k, \ quad 1 \ leqslant j \ leqslant n.}$

Невырожденная седловая точка, г ⁰ ∈ С ^п, голоморфная функцией S ( г) является критической точкой функции (т.е. ∇ S ( г ⁰) = 0), где матрица Гесса функции имеет в неисчезающей определитель (т.е.). ${\ Displaystyle \ Det S '' _ {zz} (z ^ {0}) \ neq 0}$

Следующее является основным инструментом для построения асимптотики интегралов в случае невырожденной седловой точки:

Комплексная лемма Морса

Морзе лемма для вещественных функций обобщают следующий образом для голоморфных функций : вблизи невырожденной седловой точки г ⁰ голоморфной функции S ( г), существует координаты в терминах которых S ( г) - С ( г ⁰) точно квадратичный. Чтобы сделать это точным, пусть S - голоморфная функция с областью определения W ⊂ C ⁿ, и пусть z ⁰ в W - невырожденная седловая точка S, то есть ∇ S ( z ⁰) = 0 и. Тогда существуют окрестности U ⊂ W из г ⁰ и V ⊂ C ^п о ш = 0, и биективном голоморфной функции ф  : V → U с ф (0) = г ⁰ такое, что ${\ Displaystyle \ Det S '' _ {zz} (z ^ {0}) \ neq 0}$

${\ displaystyle \ forall w \ in V: \ qquad S ({\ boldsymbol {\ varphi}} (w)) = S (z ^ {0}) + {\ frac {1} {2}} \ sum _ { j = 1} ^ {n} \ mu _ {j} w_ {j} ^ {2}, \ quad \ det {\ boldsymbol {\ varphi}} _ {w} '(0) = 1,}$

Здесь μ j - собственные значения матрицы. ${\ displaystyle S_ {zz} '' (z ^ {0})}$

Иллюстрация комплексной леммы Морса Доказательство комплексной леммы Морса  -

Следующее доказательство является прямым обобщением доказательства действительной леммы Морса, которое можно найти в. Начнем с демонстрации

Вспомогательное заявление. Пусть F   : С ^п → С быть голоморфна в окрестности начала координат и F  (0) = 0. Тогда в некоторой окрестности существуют функции g i  : C ⁿ → C такие, что    

${\ Displaystyle е (г) = \ сумма _ {я = 1} ^ {п} г_ {я} г_ {я} (г),}$

где каждый г я является голоморфным и

${\ displaystyle g_ {i} (0) = \ left. {\ tfrac {\ partial f (z)} {\ partial z_ {i}}} \ right | _ {z = 0}.}$

От личности

${\ displaystyle f (z) = \ int _ {0} ^ {1} {\ frac {d} {dt}} f \ left (tz_ {1}, \ cdots, tz_ {n} \ right) dt = \ sum _ {i = 1} ^ {n} z_ {i} \ int _ {0} ^ {1} \ left. {\ frac {\ partial f (z)} {\ partial z_ {i}}} \ right | _ {z = (tz_ {1}, \ ldots, tz_ {n})} dt,}$

мы заключаем, что

${\ displaystyle g_ {i} (z) = \ int _ {0} ^ {1} \ left. {\ frac {\ partial f (z)} {\ partial z_ {i}}} \ right | _ {z = (tz_ {1}, \ ldots, tz_ {n})} dt}$

а также

${\ displaystyle g_ {i} (0) = \ left. {\ frac {\ partial f (z)} {\ partial z_ {i}}} \ right | _ {z = 0}.}$

Без ограничения общности переводим начало координат в z ⁰, так что z ⁰ = 0 и S (0) = 0. Используя вспомогательное утверждение, имеем

${\ displaystyle S (z) = \ sum _ {i = 1} ^ {n} z_ {i} g_ {i} (z).}$

Поскольку начало координат - седловая точка,

${\ displaystyle \ left. {\ frac {\ partial S (z)} {\ partial z_ {i}}} \ right | _ {z = 0} = g_ {i} (0) = 0,}$

мы также можем применить вспомогательное утверждение к функциям g i ( z) и получить

${\ Displaystyle S (z) = \ sum _ {i, j = 1} ^ {n} z_ {i} z_ {j} h_ {ij} (z).}$ (1)

Напомним, что произвольная матрица A может быть представлена ​​как сумма симметричной A ^{( s)} и антисимметричной A ^{( a)} матриц,

${\ Displaystyle A_ {ij} = A_ {ij} ^ {(s)} + A_ {ij} ^ {(a)}, \ qquad A_ {ij} ^ {(s)} = {\ tfrac {1} { 2}} \ left (A_ {ij} + A_ {ji} \ right), \ qquad A_ {ij} ^ {(a)} = {\ tfrac {1} {2}} \ left (A_ {ij} - A_ {ji} \ right).}$

Сжатие любой симметричной матрицы B с произвольной матрицей A есть

${\ displaystyle \ sum _ {i, j} B_ {ij} A_ {ij} = \ sum _ {i, j} B_ {ij} A_ {ij} ^ {(s)},}$

(2)

т.е. антисимметричный компонент A не вносит вклада, потому что

${\ displaystyle \ sum _ {i, j} B_ {ij} C_ {ij} = \ sum _ {i, j} B_ {ji} C_ {ji} = - \ sum _ {i, j} B_ {ij} C_ {ij} = 0.}$

Таким образом, h ij ( z) в уравнении (1) можно считать симметричным относительно перестановки индексов i и j. Обратите внимание, что

${\ displaystyle \ left. {\ frac {\ partial ^ {2} S (z)} {\ partial z_ {i} \ partial z_ {j}}} \ right | _ {z = 0} = 2h_ {ij} (0);}$

следовательно, det ( h ij (0)) ≠ 0, поскольку начало координат - невырожденная седловая точка.

Покажем по индукции, что существуют локальные координаты u = ( u 1,... u n), z = ψ ( u), 0 = ψ (0), такие, что

${\ displaystyle S ({\ boldsymbol {\ psi}} (u)) = \ sum _ {i = 1} ^ {n} u_ {i} ^ {2}.}$ (3)

Сначала предположим, что существуют локальные координаты y = ( y 1,... y n), z = φ ( y), 0 = φ (0), такие, что

${\ displaystyle S ({\ boldsymbol {\ phi}} (y)) = y_ {1} ^ {2} + \ cdots + y_ {r-1} ^ {2} + \ sum _ {i, j = r } ^ {n} y_ {i} y_ {j} H_ {ij} (y),}$ (4)

где H ij симметричен в силу уравнения (2). Линейной заменой переменных ( y r,... y n) можно гарантировать, что H rr (0) ≠ 0. Из цепного правила имеем

${\ displaystyle {\ frac {\ partial ^ {2} S ({\ boldsymbol {\ phi}} (y))} {\ partial y_ {i} \ partial y_ {j}}} = \ sum _ {l, k = 1} ^ {n} \ left. {\ frac {\ partial ^ {2} S (z)} {\ partial z_ {k} \ partial z_ {l}}} \ right | _ {z = {\ boldsymbol {\ phi}} (y)} {\ frac {\ partial \ phi _ {k}} {\ partial y_ {i}}} {\ frac {\ partial \ phi _ {l}} {\ partial \ phi_ { j}}} + \ sum _ {k = 1} ^ {n} \ left. {\ frac {\ partial S (z)} {\ partial z_ {k}}} \ right | _ {z = {\ boldsymbol {\ phi}} (y)} {\ frac {\ partial ^ {2} \ phi _ {k}} {\ partial y_ {i} \ partial y_ {j}}}}$

Следовательно:

${\ displaystyle S '' _ {yy} ({\ boldsymbol {\ phi}} (0)) = {\ boldsymbol {\ phi}} '_ {y} (0) ^ {T} S' '_ {zz } (0) {\ boldsymbol {\ phi}} '_ {y} (0), \ qquad \ det {\ boldsymbol {\ phi}}' _ {y} (0) \ neq 0;}$

откуда,

${\ displaystyle 0 \ neq \ det S '' _ {yy} ({\ boldsymbol {\ phi}} (0)) = 2 ^ {r-1} \ det \ left (2H_ {ij} (0) \ right).}$

Матрица ( H ij (0)) может быть преобразована в нормальную форму Жордана : ( H ij (0)) = LJL ⁻¹, если L дает желаемое невырожденное линейное преобразование, а диагональ матрицы J содержит ненулевые собственные значения из ( H ij (0)). Если H ij (0) ≠ 0, то в силу непрерывности H ij ( y) оно также должно быть отличным от нуля в некоторой окрестности начала координат. Введя, пишем ${\ Displaystyle {\ тильда {H}} _ {ij} (y) = H_ {ij} (y) / H_ {rr} (y)}$

${\ Displaystyle {\ begin {align} S ({\ boldsymbol {\ varphi}} (y)) = amp; y_ {1} ^ {2} + \ cdots + y_ {r-1} ^ {2} + H_ {rr } (y) \ sum _ {i, j = r} ^ {n} y_ {i} y_ {j} {\ tilde {H}} _ {ij} (y) \\ = amp; y_ {1} ^ {2 } + \ cdots + y_ {r-1} ^ {2} + H_ {rr} (y) \ left [y_ {r} ^ {2} + 2y_ {r} \ sum _ {j = r + 1} ^ {n} y_ {j} {\ tilde {H}} _ {rj} (y) + \ sum _ {i, j = r + 1} ^ {n} y_ {i} y_ {j} {\ tilde { H}} _ {ij} (y) \ right] \\ = amp; y_ {1} ^ {2} + \ cdots + y_ {r-1} ^ {2} + H_ {rr} (y) \ left [\ left (y_ {r} + \ sum _ {j = r + 1} ^ {n} y_ {j} {\ tilde {H}} _ {rj} (y) \ right) ^ {2} - \ left ( \ sum _ {j = r + 1} ^ {n} y_ {j} {\ tilde {H}} _ {rj} (y) \ right) ^ {2} \ right] + H_ {rr} (y) \ sum _ {i, j = r + 1} ^ {n} y_ {i} y_ {j} {\ tilde {H}} _ {ij} (y) \ end {выровнено}}}$

Руководствуясь последним выражением, введем новые координаты z = η ( x), 0 = η (0),

${\ displaystyle x_ {r} = {\ sqrt {H_ {rr} (y)}} \ left (y_ {r} + \ sum _ {j = r + 1} ^ {n} y_ {j} {\ tilde) {H}} _ {rj} (y) \ right), \ qquad x_ {j} = y_ {j}, \ quad \ forall j \ neq r.}$

Замена переменных y ↔ x локально обратима, поскольку соответствующий якобиан отличен от нуля,

${\ displaystyle \ left. {\ frac {\ partial x_ {r}} {\ partial y_ {k}}} \ right | _ {y = 0} = {\ sqrt {H_ {rr} (0)}} \ left [\ delta _ {r, \, k} + \ sum _ {j = r + 1} ^ {n} \ delta _ {j, \, k} {\ tilde {H}} _ {jr} (0)\Правильно].}$

Следовательно,

${\ displaystyle S ({\ boldsymbol {\ eta}} (x)) = {x} _ {1} ^ {2} + \ cdots + {x} _ {r} ^ {2} + \ sum _ {i, j = r + 1} ^ {n} {x} _ {i} {x} _ {j} W_ {ij} (x).}$ (5)

Сравнивая уравнения (4) и (5), заключаем, что уравнение (3) проверено. Обозначая собственные значения из по ц J, уравнение (3) можно переписать в виде ${\ displaystyle S '' _ {zz} (0)}$

${\ displaystyle S ({\ boldsymbol {\ varphi}} (w)) = {\ frac {1} {2}} \ sum _ {j = 1} ^ {n} \ mu _ {j} w_ {j} ^ {2}.}$ (6)

Следовательно,

${\ displaystyle S '' _ {ww} ({\ boldsymbol {\ varphi}} (0)) = {\ boldsymbol {\ varphi}} '_ {w} (0) ^ {T} S' '_ {zz } (0) {\ boldsymbol {\ varphi}} '_ {w} (0),}$ (7)

Из уравнения (6) следует, что. Джордан нормальная форма из гласит, где J г является верхней диагональная матрица, содержащая собственные значения и DET P ≠ 0 ; следовательно,. Из уравнения (7) получаем ${\ Displaystyle \ Det S '' _ {ww} ({\ boldsymbol {\ varphi}} (0)) = \ mu _ {1} \ cdots \ mu _ {n}}$ ${\ displaystyle S '' _ {zz} (0)}$${\ Displaystyle S '' _ {zz} (0) = PJ_ {z} P ^ {- 1}}$ ${\ Displaystyle \ Det S '' _ {zz} (0) = \ mu _ {1} \ cdots \ mu _ {n}}$

${\ displaystyle \ det S '' _ {ww} ({\ boldsymbol {\ varphi}} (0)) = \ left [\ det {\ boldsymbol {\ varphi}} '_ {w} (0) \ right] ^ {2} \ det S '' _ {zz} (0) \ Longrightarrow \ det {\ boldsymbol {\ varphi}} '_ {w} (0) = \ pm 1.}$

Если, то замена двух переменных гарантирует это. ${\ displaystyle \ det {\ boldsymbol {\ varphi}} '_ {w} (0) = - 1}$${\ displaystyle \ det {\ boldsymbol {\ varphi}} '_ {w} (0) = + 1}$

Асимптотическое разложение в случае одной невырожденной седловой точки

Предполагать

1.  е  ( г) и С ( г) являются голоморфными функциями в открытом, ограниченном, и просто подсоединенном множестве Ω х ⊂ С ^п такоечто я х = Ω х ∩ R ^п буду подключен ;
2. ${\ Displaystyle \ Re (S (г))}$имеет единственный максимум: ровно для одной точки x ⁰ ∈ I x ;${\ displaystyle \ max _ {z \ in I_ {x}} \ Re (S (z)) = \ Re (S (x ^ {0}))}$
3. x ⁰ - невырожденная седловая точка (т. е. ∇ S ( x ⁰) = 0 и).${\ Displaystyle \ Det S '' _ {хх} (х ^ {0}) \ neq 0}$

Тогда имеет место следующая асимптотика

${\ Displaystyle I (\ lambda) \ Equiv \ int _ {I_ {x}} f (x) e ^ {\ lambda S (x)} dx = \ left ({\ frac {2 \ pi} {\ lambda}) } \ right) ^ {\ frac {n} {2}} e ^ {\ lambda S (x ^ {0})} \ left (f (x ^ {0}) + O \ left (\ lambda ^ {- 1} \ right) \ right) \ prod _ {j = 1} ^ {n} (- \ mu _ {j}) ^ {- {\ frac {1} {2}}}, \ qquad \ lambda \ to \ infty,}$ (8)

где μ J являются собственными значениями матрицы Гессе и определяются с аргументами ${\ Displaystyle S '' _ {хх} (х ^ {0})}$${\ displaystyle (- \ mu _ {j}) ^ {- {\ frac {1} {2}}}}$

${\ displaystyle \ left | \ arg {\ sqrt {- \ mu _ {j}}} \ right | lt;{\ tfrac {\ pi} {4}}.}$

(9)

Это утверждение является частным случаем более общих результатов, представленных в работе Федорюка (1987).

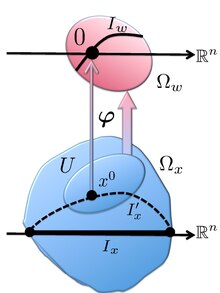
Вывод уравнения (8)  - Иллюстрация к выводу уравнения (8)

Сначала мы деформируем контур I x в новый контур, проходящий через седловую точку x ⁰ и разделяющий границу с I x. Эта деформация не меняет значения интеграла I ( λ). Мы используем комплексную лемму Морса для замены переменных интегрирования. Согласно лемме функция φ ( w) отображает окрестность x ⁰ ∈ U ⊂ Ω x на окрестность Ω w, содержащую начало координат. Интеграл I ( λ) можно разбить на два: I ( λ) = I 0 ( λ) + I 1 ( λ), где I 0 ( λ) - интеграл по, а I 1 ( λ) - по окончанию (т. Е., оставшаяся часть контура I ′ x). Поскольку последняя область не содержит седловой точки x ⁰, значение I 1 ( λ) экспоненциально меньше, чем I 0 ( λ) при λ → ∞ ; таким образом, I 1 ( λ) игнорируется. Вводя контур I w так, чтобы имеем ${\ displaystyle I '_ {x} \ subset \ Omega _ {x}}$ ${\ displaystyle U \ cap I '_ {x}}$${\ displaystyle I '_ {x} \ setminus (U \ cap I' _ {x})}$${\ Displaystyle U \ cap I '_ {x} = {\ boldsymbol {\ varphi}} (I_ {w})}$

${\ displaystyle I_ {0} (\ lambda) = e ^ {\ lambda S (x ^ {0})} \ int _ {I_ {w}} f [{\ boldsymbol {\ varphi}} (w)] \ exp \ left (\ lambda \ sum _ {j = 1} ^ {n} {\ tfrac {\ mu _ {j}} {2}} w_ {j} ^ {2} \ right) \ left | \ det { \ boldsymbol {\ varphi}} _ {w} '(w) \ right | dw.}$ (10)

Напоминая, что x ⁰ = φ (0), а также, мы разложим предэкспоненциальную функцию в ряд Тейлора и оставим только старший член нулевого порядка ${\ displaystyle \ det {\ boldsymbol {\ varphi}} _ {w} '(0) = 1}$${\ displaystyle f [{\ boldsymbol {\ varphi}} (ш)]}$

${\ displaystyle I_ {0} (\ lambda) \ приблизительно f (x ^ {0}) e ^ {\ lambda S (x ^ {0})} \ int _ {\ mathbf {R} ^ {n}} \ exp \ left (\ lambda \ sum _ {j = 1} ^ {n} {\ tfrac {\ mu _ {j}} {2}} w_ {j} ^ {2} \ right) dw = f (x ^ {0}) e ^ {\ lambda S (x ^ {0})} \ prod _ {j = 1} ^ {n} \ int _ {- \ infty} ^ {\ infty} e ^ {{\ frac { 1} {2}} \ lambda \ mu _ {j} y ^ {2}} dy.}$ (11)

Здесь мы заменили область интегрирования I w на R ^n, потому что обе содержат начало координат, которое является седловой точкой, следовательно, они равны с точностью до экспоненциально малого члена. Интегралы в правой части уравнения (11) могут быть выражены как

${\ displaystyle {\ mathcal {I}} _ {j} = \ int _ {- \ infty} ^ {\ infty} e ^ {{\ frac {1} {2}} \ lambda \ mu _ {j} y ^ {2}} dy = 2 \ int _ {0} ^ {\ infty} e ^ {- {\ frac {1} {2}} \ lambda \ left ({\ sqrt {- \ mu _ {j}} } y \ right) ^ {2}} dy = 2 \ int _ {0} ^ {\ infty} e ^ {- {\ frac {1} {2}} \ lambda \ left | {\ sqrt {- \ mu _ {j}}} \ right | ^ {2} y ^ {2} \ exp \ left (2i \ arg {\ sqrt {- \ mu _ {j}}} \ right)} dy.}$ (12)

Из этого представления мы заключаем, что условие (9) должно быть выполнено для того, чтобы правая и левая части уравнения (12) совпадали. Согласно предположению 2, это отрицательно определенная квадратичная форма (а именно,), подразумевающая существование интеграла, который легко вычисляется ${\ Displaystyle \ Re \ left (S_ {xx} '' (x ^ {0}) \ right)}$ ${\ Displaystyle \ Re (\ му _ {j}) lt;0}$${\ displaystyle {\ mathcal {I}} _ {j}}$

${\ displaystyle {\ mathcal {I}} _ {j} = {\ frac {2} {{\ sqrt {- \ mu _ {j}}} {\ sqrt {\ lambda}}}} \ int _ {0 } ^ {\ infty} e ^ {- {\ frac {\ xi ^ {2}} {2}}} d \ xi = {\ sqrt {\ frac {2 \ pi} {\ lambda}}} (- \ mu _ {j}) ^ {- {\ frac {1} {2}}}.}$

Уравнение (8) также можно записать в виде

${\ displaystyle I (\ lambda) = \ left ({\ frac {2 \ pi} {\ lambda}} \ right) ^ {\ frac {n} {2}} e ^ {\ lambda S (x ^ {0 })} \ left (\ det (-S_ {xx} '' (x ^ {0})) \ right) ^ {- {\ frac {1} {2}}} \ left (f (x ^ {0 }) + O \ left (\ lambda ^ {- 1} \ right) \ right),}$ (13)

где филиал

${\ displaystyle {\ sqrt {\ det \ left (-S_ {xx} '' (x ^ {0}) \ right)}}}$

выбирается следующим образом

${\ displaystyle {\ begin {align} \ left (\ det \ left (-S_ {xx} '' (x ^ {0}) \ right) \ right) ^ {- {\ frac {1} {2}} } amp; = \ exp \ left (-i {\ text {Ind}} \ left (-S_ {xx} '' (x ^ {0}) \ right) \ right) \ prod _ {j = 1} ^ { n} \ left | \ mu _ {j} \ right | ^ {- {\ frac {1} {2}}}, \\ {\ text {Ind}} \ left (-S_ {xx} '' (x ^ {0}) \ right) amp; = {\ tfrac {1} {2}} \ sum _ {j = 1} ^ {n} \ arg (- \ mu _ {j}), amp;amp; | \ arg (- \ mu _ {j}) | lt;{\ tfrac {\ pi} {2}}. \ end {align}}}$

Рассмотрим важные частные случаи:

• Если S ( x) является действительным знаком для действительного x и x ⁰ в R ⁿ (он же многомерный метод Лапласа), то

${\ displaystyle {\ text {Ind}} \ left (-S_ {xx} '' (x ^ {0}) \ right) = 0.}$

• Если S ( x) чисто мнимый для действительного x (т. Е. Для всех x в R ⁿ) и x ⁰ в R ⁿ (также известный как метод многомерной стационарной фазы), то${\ Displaystyle \ Re (S (х)) = 0}$

${\ displaystyle {\ text {Ind}} \ left (-S_ {xx} '' (x ^ {0}) \ right) = {\ frac {\ pi} {4}} {\ text {sign}} S_ {xx} '' (x_ {0}),}$

где обозначает сигнатуру матрицы, равную количеству отрицательных собственных значений минус количество положительных. Примечательно, что в приложениях метода стационарной фазы к многомерному ВКБ-приближению в квантовой механике (а также в оптике) Ind связан с индексом Маслова, см., Например, Chaichian amp; Demichev (2001) и Schulman (2005).${\ displaystyle {\ text {sign}} S_ {xx} '' (x_ {0})}$ ${\ displaystyle S_ {xx} '' (x_ {0})}$

Если функция S ( x) имеет несколько изолированных невырожденных седловых точек, т. Е.

${\ displaystyle \ nabla S \ left (x ^ {(k)} \ right) = 0, \ quad \ det S '' _ {xx} \ left (x ^ {(k)} \ right) \ neq 0, \ quad x ^ {(k)} \ in \ Omega _ {x} ^ {(k)},}$

куда

${\ displaystyle \ left \ {\ Omega _ {x} ^ {(k)} \ right \} _ {k = 1} ^ {K}}$

приведено открытое покрытие из Ом х, то вычисление интегральной асимптотики сводятся к случаю одной седловой точки посредством использования разбиения единицы. Разбиение единицы позволяет построить множество непрерывных функций р к ( х): Ω х → [0, 1], 1 ≤ K ≤ K, такой, что

${\ displaystyle {\ begin {align} \ sum _ {k = 1} ^ {K} \ rho _ {k} (x) amp; = 1, amp;amp; \ forall x \ in \ Omega _ {x}, \\\ rho _ {k} (x) amp; = 0 amp;amp; \ forall x \ in \ Omega _ {x} \ setminus \ Omega _ {x} ^ {(k)}. \ end {align}}}$

Откуда,

${\ displaystyle \ int _ {I_ {x} \ subset \ Omega _ {x}} f (x) e ^ {\ lambda S (x)} dx \ Equiv \ sum _ {k = 1} ^ {K} \ int _ {I_ {x} \ subset \ Omega _ {x}} \ rho _ {k} (x) f (x) e ^ {\ lambda S (x)} dx.}$

Следовательно, при λ → ∞ имеем:

${\ displaystyle \ sum _ {k = 1} ^ {K} \ int _ {{\ text {окрестность}} x ^ {(k)}} f (x) e ^ {\ lambda S (x)} dx = \ left ({\ frac {2 \ pi} {\ lambda}} \ right) ^ {\ frac {n} {2}} \ sum _ {k = 1} ^ {K} e ^ {\ lambda S \ left (x ^ {(k)} \ right)} \ left (\ det \ left (-S_ {xx} '' \ left (x ^ {(k)} \ right) \ right) \ right) ^ { - {\ frac {1} {2}}} f \ left (x ^ {(k)} \ right),}$

где уравнение (13) использовалось на последнем этапе, а предэкспоненциальная функция f  ( x) по крайней мере должна быть непрерывной.  

Когда ∇ S ( z ⁰) = 0 и, точка z ⁰ ∈ C ⁿ называется вырожденной седловой точкой функции S ( z). ${\ Displaystyle \ Det S '' _ {zz} (z ^ {0}) = 0}$

Вычисление асимптотики

${\ Displaystyle \ int е (х) е ^ {\ лямбда S (х)} dx,}$

когда λ → ∞, функция   f  ( x) непрерывна и S ( z) имеет вырожденную седловую точку, это очень сложная задача, решение которой во многом опирается на теорию катастроф. Здесь теория катастроф заменяет лемму Морса, справедливую только в невырожденном случае, для преобразования функции S ( z) в одно из множества канонических представлений. Подробнее см., Например, Poston amp; Stewart (1978) и Fedoryuk (1987).

Интегралы с вырожденными седловыми точками естественным образом появляются во многих приложениях, включая оптические каустики и многомерное ВКБ-приближение в квантовой механике.

Другие случаи, такие как, например, f  ( x) и / или S ( x), являются разрывными или когда экстремум S ( x) находится на границе области интеграции, требуют особой осторожности (см., Например, Fedoryuk (1987) и Вонг (1989)).  

Расширением метода наискорейшего спуска является так называемый метод нелинейной стационарной фазы / наискорейшего спуска. Здесь вместо интегралов необходимо асимптотически оценивать решения задач факторизации Римана – Гильберта.

Учитывая контур C в комплексной сфере, функцию f, определенную на этом контуре и особую точку, скажем бесконечность, ищется функция M, голоморфная вдали от контура C, с заданным скачком через C и с заданной нормализацией на бесконечности. Если f и, следовательно, M являются матрицами, а не скалярами, это проблема, которая, как правило, не допускает явного решения.

Тогда возможна асимптотическая оценка в соответствии с методом линейной стационарной фазы / наискорейшего спуска. Идея состоит в том, чтобы асимптотически свести решение данной проблемы Римана – Гильберта к решению более простой, явно решаемой проблемы Римана – Гильберта. Теорема Коши используется для обоснования деформаций контура скачка.

Нелинейная стационарная фаза была введена Дейфтом и Чжоу в 1993 году на основе более ранней работы русского математика Александра Итца. (Собственно говоря) нелинейный метод наискорейшего спуска был введен Камвиссисом, К. Маклафлином и П. Миллером в 2003 году на основе предыдущей работы Лакса, Левермора, Дейфта, Венакидеса и Чжоу. Как и в линейном случае, контуры наискорейшего спуска решают задачу минимума-максимума. В нелинейном случае они оказываются «S-образными кривыми» (определенными в другом контексте еще в 80-х годах Шталем, Гончаром и Рахмановым).

Метод нелинейной стационарной фазы / наискорейшего спуска имеет приложения к теории солитонных уравнений и интегрируемым моделям, случайным матрицам и комбинаторике.

• Интеграл Пирси
• Приближение стационарной фазы
• Метод Лапласа

• Чайчян, М.; Демичев А. (2001), Интегралы по траекториям в физике, том 1: Стохастический процесс и квантовая механика, Тейлор и Фрэнсис, с. 174, ISBN   075030801X
• Дебай, П. (1909), "Näherungsformeln für die Zylinderfunktionen für große Werte des Arguments und unbeschränkt veränderliche Werte des Index", Mathematische Annalen, 67 (4): 535–558, doi : 10.1007 / BF01450097 Английский перевод в Дебай, Питер Дж. У. (1954), Сборник статей Питера Дж. В. Дебая, Interscience Publishers, Inc., Нью-Йорк, ISBN   978-0-918024-58-9, Руководство по ремонту   0063975
• Deift, P.; Чжоу, X. (1993), "Метод наискорейшего спуска для осцилляторных задач Римана-Гильберта. Асимптотика для уравнения MKdV", Ann. математики., Анналы математики, Vol. 137, No. 2, 137 (2), стр. 295–368, arXiv : math / 9201261, doi : 10.2307 / 2946540, JSTOR   2946540.
• Эрдели А. (1956), Асимптотические разложения, Дувр..
• Федорюк, М.В. (2001) [1994], "Метод перевала", Энциклопедия математики, EMS Press.
• Федорюк М. В. Асимптотика: интегралы и ряды, Наука, М., 1987. [на русском].
• Kamvissis, S.; McLaughlin, KT-R.; Миллер, П. (2003), "Полуклассические солитонные ансамбли для фокусирующего нелинейного уравнения Шредингера", Annals of Mathematics Studies, Princeton University Press, 154.
• Риман, Б. (1863), Sullo svolgimento del quoziente di due serie ipergeometriche in frazione contina infinita (Неопубликованная заметка, воспроизведенная в сборнике статей Римана.)
• Siegel, CL (1932), "Uber Riemanns Nachlaß zur analytischen Zahlentheorie", Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, 2: 45–80Перепечатано в Gesammelte Abhandlungen, Vol. 1. Берлин: Springer-Verlag, 1966.
  • Переведено на Deift, Перси; Чжоу, Синь (2018), «О Riemanns Nachlass для аналитической теории чисел: перевод Uber Зигеля», arXiv : 1810.05198 [ math.HO ].
• Постон, Т.; Стюарт И. (1978), Теория катастроф и ее приложения, Pitman.
• Шульман, LS (2005), "Глава 17: Фаза квазиклассической амплитуды", Методы и приложения интеграции путей, Дувр, ISBN   0486445283
• Вонг Р. (1989), Асимптотические приближения интегралов, Academic Press.