Седловая точка

Седловая точка (красная) на графике z = x − y (гиперболический параболоид )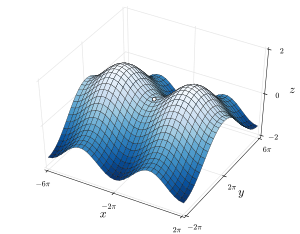 Седловая точка между двумя холмами (пересечение восьмерки $z\; \{\backslash \; displaystyle\; z\}$-contour)

В математике, седловая точка или точка минимакса является точка на поверхности графика функции, где наклоны (производные) в ортогональных направлениях равны нулю (критическая точка ), но который не является локальным экстремумом функции. Примером седловой точки является критическая точка с относительным минимумом вдоль одного осевого направления ( между пиками) и при относительном максимуме вдоль оси пересечения. Однако точка перевала не обязательно должна быть в этой форме. Например, функция $f\; (x,\; y)\; =\; x\; 2\; +\; y\; 3\; \{\backslash \; displaystyle\; f\; (x,\; y)\; =\; x\; ^\; \{2\}\; +\; y\; ^\; \{3\}\}$имеет критическую точку в $(0,\; 0)\; \{\backslash \; displaystyle\; (0,0)\}$это седловая точка, поскольку она не является ни относительным максимумом, ни относительным минимумом, но не имеет относительного максимума или относительного минимума в $y\; \{\backslash \; displaystyle\; y\}$-направление.

Название происходит от того факта, что прототипом в двух измерениях является поверхность , которая изгибается вверх в одном направлении и изгибается вниз в другом направлении, напоминая седло для верховой езды . или горный перевал между двумя пиками, образующий седловину рельефа. В терминах контурных линий, седловая точка в двух измерениях порождает контурный график или трассу, в которой контур, соответствующий значению седловой точки, кажется, пересекает сам себя.

• 1 Математическое обсуждение
• 2 Поверхность седла
• 3 Примеры
• 4 Другое использование
• 5 См. Также
• 6 Ссылки
  • 6.1 Цитаты
  • 6.2 Источники
• 7 Дополнительная литература
• 8 Внешние ссылки

Простой критерий для проверки того, является ли данная стационарная точка действительной функции F (x, y) двух вещественных переменных седлом точка состоит в том, чтобы вычислить матрицу Гессе функции в этой точке: если гессиан неопределенный, то эта точка является седловой точкой. Например, матрица Гессе функции $z\; =\; x\; 2\; -\; y\; 2\; \{\backslash \; displaystyle\; z\; =\; x\; ^\; \{2\}\; -y\; ^\; \{2\}\}$в стационарной точке $(\; x,\; y,\; z)\; =\; (0,\; 0,\; 0)\; \{\backslash \; displaystyle\; (x,\; y,\; z)\; =\; (0,0,0)\}$- матрица

$[2\; 0\; 0\; -\; 2]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 0\; \backslash \backslash \; 0\; -2\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\}$

, которое не определено. Следовательно, эта точка является седловой. Этот критерий дает лишь достаточное условие. Например, точка $(0,\; 0,\; 0)\; \{\backslash \; displaystyle\; (0,0,0)\}$является седловой точкой для функции $z\; =\; x\; 4\; -\; y\; 4,\; \{\backslash \; displaystyle\; z\; =\; x\; ^\; \{4\}\; -y\; ^\; \{4\},\}$но матрица Гессе этой функции в начале координат является нулевой матрицей, которая не является неопределенной.

В самых общих чертах, седловая точка для сглаженной функции (чей график является кривой, поверхность или гиперповерхность ) - это неподвижная точка, такая что кривая / поверхность / и т. Д. в окрестности этой точки не находится полностью ни с одной стороны от касательного пространства в этой точке.

График y = x с седловой точкой в ​​0

В области одного измерения седловой точкой является точка, которая одновременно является стационарной точкой и точка перегиба. Поскольку это точка перегиба, это не локальный экстремум.

Гиперболический параболоид Модель эллиптического гиперболоида из одинарного листа 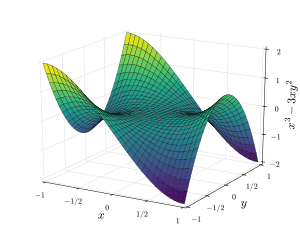A седло обезьяны.

A седловая поверхность - это гладкая поверхность, содержащая одну или несколько седловых точек.

Классическими примерами двумерных седловых поверхностей в евклидовом пространстве являются поверхности второго порядка, гиперболический параболоид $z\; =\; x\; 2\; -\; y\; 2\; \{\backslash \; displaystyle\; z\; =\; x\; ^\; \{2\}\; -y\; ^\; \{2\}\}$(который часто называют «седловидной поверхностью» или «стандартной седловидной поверхностью») и гиперболоидом одного листа. Картофельные чипсы Pringles или чипсы являются повседневным примером гиперболической параболоидной формы.

Седловые поверхности имеют отрицательную гауссову кривизну, что отличает их от выпуклых / эллиптических поверхностей, которые имеют положительную гауссову кривизну. Классическая седловая поверхность третьего порядка - это седло обезьяны.

В игре для двух игроков с нулевой суммой, определенной на непрерывном пространстве, равновесие точка - это седловая точка.

Для линейной автономной системы второго порядка критическая точка является седловой точкой, если характеристическое уравнение имеет одно положительное и одно отрицательное действительное собственное значение.

При оптимизации с учетом ограничений равенства, условия первого порядка описывают седловую точку лагранжиана.

В динамических системах, если динамика заданное дифференцируемым отображением f, то точка является гиперболической тогда и только тогда, когда дифференциал (где n - период точки) не имеет собственного значения на (комплексной) единичной окружности при вычислении в точке. Тогда седловая точка - это гиперболическая периодическая точка, стабильные и неустойчивые многообразия которой имеют размерность, отличную от нуля.

Седловая точка матрицы - это элемент, который является одновременно самым большим элементом в столбце и самым маленьким элементом в строке.

• Метод перевала является расширением метода Лапласа для аппроксимации интегралов
• Экстремум
• Тест производной
• Точка гиперболического равновесия
• Теорема минимакса
• Макс-мин неравенство
• Седло обезьяны
• Теорема о горном перевале

Цитаты

Источники

• Гильберт, Дэвид ; Кон-Фоссен, Стефан (1952). Геометрия и воображение (2-е изд.). Челси. ISBN 0-8284-1087-9.

• СМИ, относящиеся к Saddle Point на Wikimedia Commons