Собственные значения и собственные свойства

Векторы, которые предоставляются в их скалярные кратные, и связанные скаляры

В линейной алгебре, собственный вектор () или характерный вектор линейного преобразования является ненулевым вектором который изменится на коэффициент скаляр, когда к нему применяется линейное преобразование. Соответствующее собственное значение, часто обозначаемое $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, является коэффициентом масштабирования собственного вектора.

Геометрически, собственный вектор, соответствующий действующему ненулевому собственному значению, указывает в направлении, в котором оно растягивается преобразованием, а собственное значение является коэффициентом, на который он растянут. Если собственное значение отрицательное, направление меняется на противоположное. Грубо говоря, в многомерном векторном изображении собственный вектор не поворачивается.

Содержание

• 1 Формальное определение
• 2 Обзор
• 3 История
• 4 Собственные значения и собственные значения матриц
  • 4.1 Собственные значения и характерный многочлен
  • 4.2 Алгебраическая кратность
  • 4.3 Собственные подпространство, геометрическая кратность и собственный базис для матриц
  • 4.4 Дополнительные свойства собственных значений
  • 4.5 Левый и правый собственный вектор
  • 4.6 Диагонализация и собственное разложение
  • 4.7 Вариационная характеристика
  • 4.8 Примеры матриц
    • 4.8.1 Пример двумерной матрицы
    • 4.8.2 Пример трехмерной матрицы
    • 4.8.3 Пример трехмерной матрицы с комплексными собственными значениями
    • 4.8.4 Пример диагональной матрицы
    • 4.8.5 Пример треугольной матрицы
    • 4.8. 6 Пример матрицы с повторяющимися собственными значениями
  • 4.9 Тождество собственного вектора и собственного значения
• 5 Собственные значения и собственные функции дифференциальных операторов
  • 5.1 Приме р производного оператора
• 6 Общее определение
  • 6.1 Собственные подпространства, геометрическая кратность и собственные основы
  • 6.2 Нулевой вектор как собственный вектор
  • 6.3 Спектральная теория
  • 6.4 Ассоциативные алгебры и теория представлений
• 7 Динамические уравнения
• 8 Расчет
  • 8.1 Классический метод
    • 8.1.1 Собственные значения
    • 8.1.2 Собственные знания
  • 8.2 Простые итерационные методы
  • 8.3 Современные методы
• 9 Приложения
  • 9.1 Собственные значения геометрических преобразований
  • 9.2 Уравнение Шредингера
  • 9.3 Молекулярные орбитали
  • 9.4 Геология и гляциология
  • 9.5 Анализ главных компонентов
  • 9.6 Анализ вибрации
  • 9.7 Собственные значения
  • 9.8 Тензор момента инерции
  • 9.9 Тензор напряжений
  • 9.10 Графики
  • 9.11 Базовое число воспроизведения
• 10 См. Также
• 11 Примечания
  • 11.1 Цитаты
• 12 Источники
• 13 Дополнительная литература
• 14 Внешние ссылки
  • 14.1 Теория
  • 14.2 Демонстрационные апплеты

Формальное определение

Если T является линейным преобразованием из пространства V над полем F в себе и v является ненулевым вектором в V, тогда v является собственным вектором T, если T (v ) является скалярным кратным v . Это можно записать как

$T\; (v)\; =\; \lambda \; v,\; \{\backslash \; displaystyle\; T\; (\backslash \; mathbf\; \{v\})\; =\; \backslash \; lambda\; \backslash \; mathbf\; \{v\},\}$

, где λ - скаляр в F, известный как собственное значение, характеристическое значение или характеристический корень, связанное с v.

Существует прямое соответствие между квадратными матрицами размером n на n и линейные преобразования из n-мерного удобств пространства в себе при любом базисе Пространства. Следовательно, в конечном счете это эквивалентно определению собственных значений и собственных векторов, используя либо язык матриц, либо язык линейных преобразований.

Если V конечно, приведенное выше уравнение эквивалентно

$A\; u\; =\; \lambda \; u.\; \{\backslash \; displaystyle\; A\; \backslash \; mathbf\; \{u\}\; =\; \backslash \; lambda\; \backslash \; mathbf\; \{u\}.\}$

где A - это матричное представление T, а u - вектор координат v.

Обзор

Собственные значения и конструкцию занимают видное место при анализе линейных преобразований. Префикс eigen- заимствован из немецкого eigen (родственного английскому слову собственное ) для « характерный »,« собственный ». Первоначально используемый для главных осей вращательного движения Твердый тел, собственные значения и собственные разработки имеют широкий спектр приложений, например, в анализ устойчивости, анализ вибрации, атомные орбитали, распознавание лиц и диагонализация матрицы.

По сути, собственный вектор v линейного преобразования T - ненулевой вектор, который при применении к нему не меняет направления. Применение T к собственному вектору масштабирует собственный вектор на скалярное значение λ, называемое определенное значение. Это условие можно записать как уравнение

$T\; (v)\; =\; \lambda \; v,\; \{\backslash \; displaystyle\; T\; (\backslash \; mathbf\; \{v\})\; =\; \backslash \; lambda\; \backslash \; mathbf\; \{v\},\}$

, называемое уравнение собственными значениями или собственное уравнение . В общем, λ может быть любым скаляром. Например, λ может быть отрицательным, и в этом случае он может быть нулевым или противоположным как часть масштабирования, или может быть нулевым или комплексным.

в этом отображении красной стрелкой меняет направление, а синяя стрелка - нет. Синяя стрелка является собственным вектором этого изображения сдвига, поскольку он не меняет направления, поскольку его длина не изменилась, его собственное значение равно 1.

Пример Мона Лиза, изображенный здесь, представляет собой простую иллюстрацию. Каждую точку на картине можно представить как вектор, указывающий от центра картины к этой точке. Линейное преобразование в этом примере называется преобразованием сдвига. Точки в верхней половине перемещаются вправо, а точка в нижней половине - влево, пропорционально тому, насколько они удалены от горизонтальной оси, проходящей через середину рисунка. Таким образом, указывающие на каждую точку исходного изображения, наклоняются вправо или влево, а в результате становится длиннее или короче. Точки вдоль горизонтальной оси вообще не перемещаются при использовании этого преобразования. Следовательно, любой вектор, который указывает прямо вправо или влево без вертикального компонента, является собственным вектором этого преобразования, поскольку отображает не меняет своего направления. Более того, все эти компоненты имеют собственное значение.

Линейные преобразования могут принимать различные различные формы, позволяющие принимать различные формы в различных формах. Например, линейное преобразование может быть дифференциальным оператором, например $ddx\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{d\}\; \{dx\}\}\}$, и в этом случае собственные функции называются собственными функциями, которые масштабируются этим дифференциальным оператором, например

$ddxe\; \lambda \; x\; =\; \lambda \; e\; \lambda \; x.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; e\; ^\; \{\backslash \; lambda\; x\}\; =\; \backslash \; lambda\; e\; ^\; \{\backslash \; lambda\; x\}.\}$

В качестве альтернативы линейное преобразование может принимать форму матрицы размера n на n, и в этом случае собственные компоненты должны предоставить собой матричное умножение на 1.. v, {\ displaystyle Av = \ lambda v,}

где вектор v представляет собой матрицу размером n 1. Для построения собственных значений матрицы - например, 293>ее диагонализации.

Собственные значения и собственные ресурсы дают начало многим системным математическим понятиям, и префикс собственным-широко используемым при их именовании:

• Набор всех собственных векторов линейного преобразования, каждый из которых соединен со своим собственным размером, называется собственной системой этого преобразования.
• Набор всех собственных векторов T, соответствующему одному и тому же собственному значению, с нулевым вектором, называется собственное подпространство вместе, или характеристическое пространство T, связанное с этим собственным значение.
• Если набор собственных векторов T образует > области T, то этот базис называется eigenbasis .

History

Собственные значения ввод часто вводятся в контексте линейной алгебры или теории матриц. Исторически, однако, они возникли при изучении квадратичных форм и дифференциальных уравнений.

В 18 веке Леонард Эйлер изучал вращательное движение твердого тела. body, и обнаружил главных осей. Джозеф-Луи Лагранж понял, что главные оси являются собственными инструментами матрицы инерции.

В начале 19 века Огюстен-Луи Коши увидел, как их работа может быть применена для классификации квадратичных поверхностей, и обобщил их произвольные размеры. Коши также ввел термин racine caractéristique (характеристический корень) для того, что теперь называется соответствующим; его член сохранился в в характеристическом уравнении.

Позже Жозеф Фурье использовал работу Лагранжа и Пьера-Симона Лапласа для решения уравнения теплопроводности с помощью разделение чисел в своей знаменитой книге 1822 года Аналитическая теория де ла чалер. Шарль-Франсуа Штурм развил идеи Фурье и обратил на них внимание Коши, который объединил их со своими идеями и пришел к тому, что реальные симметричные матрицы имеют действительные собственные значения. Чарльз Эрмит в 1855 году расширил это до того, что сейчас называется эрмитовыми матрицами.

Примерно в то же время Франческо Бриоши доказал, что собственные значения ортогональных матриц лежат на единичной окружности, и Альфред Клебш нашел соответствующий результат для кососимметричных матриц. Наконец, Карл Вейерштрасс разъяснил аспект теории устойчивости, начатой ​​Лапласом, осознав, что дефектные матрицы могут вызвать нестабильность.

Тем временем Джозеф Лиувилль изучал задачи на собственные значения, аналогичные задачи Штурма; дисциплина, выросшая из их работы, теперь называется теорией Штурма - Лиувилля. Шварц изучил первое собственное значение уравнения Лапласа в общих областях ближе к концу 19 век, в то время как Пуанкаре изучал уравнение Пуассона границ годами позже.

В начале 20 века Дэвид Гильберт изучал собственные значения из интегральных операторов, рассматривая операторы как бесконечные матрицы. Он был первым, кто использовал немецкое слово «собственное», что означает «собственные», для обозначения значений и собственных векторов в 1904 году, хотя, возможно, он следовал аналогичному использованию Германа фон Гельмгольца. Некоторое время стандартным термином на английском языке было «собственное значение», но сегодня стандартом является более характерный термин «собственное значение».

Первый числовой алгоритм для вычислений значений и собственных векторов появился в 1929 году, когда Ричард фон Мизес опубликовал метод силы. Один из самых популярных методов сегодня, QR-алгоритм, был независимо предложен Джоном Г.Ф. Фрэнсисом и Верой Кублановской в 1961 году.

Собственные значения и собственные свойства матриц

Собственные значения и собственные ценности часто знакомятся со студентами в контексте курсов линейной алгебры, посвященных матрицам. Кроме того, среди численных и вычислительных приложений часто встречается линейное преобразование.

Матрица A действует, растягивая вектор x, не меняя его направления, поэтому x собственным вектором A.

Рассмотрим n-мерные формы, которые сформированы как список из n скаляров, например, трехмерные конструкции

$x\; =\; [1\; 3\; 4]\; и\; y\; =\; [-\; 20\; -\; 60\; -\; 80].\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; 3\; \backslash \backslash \; 4\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; quad\; \{\backslash \; t\_dv\; \{and\}\}\; \backslash \; quad\; y\; =\; \{\backslash \; begin\; \{bmatrix\}\; -20\; \backslash \backslash \; -\; 60\; \backslash \; \backslash \; -80\; \backslash \; end\; \{bmatrix\}\}.\}$

Эти виды называются скалярными кратными друг другу, или параллельными или коллинеарными, если существует скаляр λ, что

$x\; =\; \lambda \; y.\; \{\backslash \; displaystyle\; x\; =\; \backslash \; lambda\; y.\}$

В этом случае $\lambda \; =\; -\; 1/20\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; -1\; /\; 20\}$.

Теперь рассмотрим линейное преобразование n-мерных векторов, определенных матрицей A размером n на n,

$A\; v\; =\; w,\; \{\backslash \; displaystyle\; Av\; =\; w,\}$

или

$[A\; 11\; A\; 12\dots \; A\; 1\; n\; A\; 21\; A\; 22\dots \; A\; 2\; n\; ⋮\; ⋮\; \ddots \; ⋮\; AN\; 1\; AN\; 2\dots \; A\; nn]\; [v\; 1\; v\; 2\; ⋮\; vn]\; =\; [w\; 1\; w\; 2\; ⋮\; wn]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; A\_\; \{11\}\; A\_\; \{12\}\; \backslash \; ldots\; A\_\; \{1n\; \}\; \backslash \backslash \; A\_\; \{21\}\; A\_\; \{22\}\; \backslash \; ldots\; A\_\; \{2n\}\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; ddots\; \backslash \; vdots\; \backslash \backslash \; A\_\; \{n1\}\; A\_\; \{n2\}\; \backslash \; ldots\; A\_\; \{\; nn\}\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \backslash \; v\_\; \{2\}\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; v\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; w\_\; \{1\}\; \backslash \backslash \; w\_\; \{2\}\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; w\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\}$

где для каждой строки

$wi\; =\; A\; i\; 1\; v\; 1\; +\; A\; i\; 2\; v\; 2\; +\; \cdots \; +\; A\; invn\; =\; \sum \; j\; =\; 1\; n\; A\; ijvj\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; A\_\; \{i1\}\; v\_\; \{1\}\; +\; A\_\; \{i2\}\; v\_\; \{2\}\; +\; \backslash \; cdots\; +\; A\_\; \{in\}\; v\_\; \{n\}\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; A\_\; \{ij\}\; v\_\; \{j\}\}$.

Если оказывается, что v и w являются скалярными кр атными, то есть

$A\; v\; =\; w\; =\; \lambda \; v,\; \{\backslash \; displaystyle\; Av\; =\; w\; =\; \backslash \; lambda\; v,\}$

(1)

, тогда v является собственным вектором линейного преобразования A, масштабный коэффициент λ является величиной, имеющей значение этому собственному вектору. Уравнение (1) - это уравнение собственных значений для матриц A.

Уравнение (1) может быть выражено эквивалентно как

$(A\; -\; \lambda \; I)\; v\; =\; 0,\; \{\backslash \; displaystyle\; (A-\; \backslash \; lambda\; I)\; v\; =\; 0,\}$

(2)

где I - это единичная матрица n на n , а 0 - нулевой вектор.

Собственные значения и характерный полином

Уравнение (2) имеет ненулевое решение v и только тогда, когда определитель (матрицы A - λI) равен нулю. Следовательно, собственные значения A - это значения λ, которые удовлетворяют уравнению

$|\; A\; -\; \lambda \; I\; |\; =\; 0\; \{\backslash \; displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; 0\}$

(3)

Использование правил Лейбницы для определителя, левая часть уравнения (3) является полиномиальной функцией переменной λ, и степень этого полинома равно n, порядок матрицы A. Его коэффициенты зависят от элементов A, за исключением того, что его член степени n всегда равен (−1) λ. Этот многочлен называется характеристическим многочленом матрицы A. Уравнение (3) называется характеристическим уравнением или вековым уравнением A.

Основная теорема алгебры означает, что характерный многочлен матрицы A размером n × n, являющимся многочленом степени n, может быть разложен на произведение n линейных членов,

$|\; A\; -\; \lambda \; I\; |\; знак\; равно\; (\lambda \; 1\; -\; \lambda )\; (\lambda \; 2\; -\; \lambda )\; \cdots \; (\lambda \; N\; -\; \lambda ),\; \{\backslash \; displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; (\backslash \; lambda\; \_\; \{1\}\; -\; \backslash \; lambda)\; (\backslash \; lambda\; \_\; \{2\}\; -\; \backslash \; lambda)\; \backslash \; cdots\; (\backslash \; lambda\; \_\; \{n\}\; -\; \backslash \; lambda),\}$

(4)

где каждый λ я может быть действительным, но в целом является комплексным числом. Числа λ 1, λ 2,... λ n, которые не могут все иметь разные значения, являющиеся корнями полинома и собственными значениями A.

В качестве краткого примера, который более подробно описан в разделе примеров ниже, рассмотрим матрицу

$A\; =\; [2\; 1\; 1\; 2].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 1\; \backslash \backslash \; 1\; 2\; \backslash \; end\; \{bmatrix\}\}.\}$

Взяв определитель (A - λI), характерный многочлен A равен

$|\; A\; -\; \lambda \; I\; |\; =\; |\; 2\; -\; \lambda \; 1\; 1\; 2\; -\; \lambda \; |\; Знак\; равно\; 3-4\; \lambda \; +\; \lambda \; 2.\; \{\backslash \; displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; \{\backslash \; begin\; \{vmatrix\}\; 2-\; \backslash \; lambda\; 1\; \backslash \backslash \; 1\; 2-\; \backslash \; lambda\; \backslash \; end\; \{vmatrix\}\}\; =\; 3-4\; \backslash \; lambda\; +\; \backslash \; lambda\; ^\; \{2\}.\}$

Если задать указанный многочлен равным нулю, он будет иметь корни при λ = 1 и λ = 3, которые являются двумя собственными значениями A. Собственные стандарты, соответствующие каждому собственному значению, могут быть найдены путем решения компонентов v в уравнении $(A\; -\; \lambda \; I)\; v\; знак\; равно\; 0\; \{\backslash \; displaystyle\; (A-\; \backslash \; lambda\; I)\; v\; =\; 0\}$. В этой конструкции должны быть любыми ненулевыми скалярными кратными

$v\; \lambda \; =\; 1\; =\; [1\; -\; 1],\; v\; \lambda \; =\; 3\; =\; [1\; 1].\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; =\; 1\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; -\; 1\; \backslash \; end\; \{bmatrix\}\},\; \backslash \; quad\; v\; \_\; \{\backslash \; lambda\; =\; 3\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\}.\}$

Если все элементы матрицы A имеют действительные числа, то коэффициенты характеристического полинома также будут действительными числами, но собственные значения по-прежнему имеют ненулевые мнимые части. Поэтому элементы соответствующие собственные векторы также могут иметь ненулевые мнимые части. Точно так же собственные значения могут быть иррациональными числами, даже если все элементы являются рациональными числами или даже если все они являются целыми числами. Однако, если все элементы A являются алгебраическими числами, которые включают рациональные числа, то собственные значения являются комплексными алгебраическими числами.

Неверные корниительного многочлена с действующими элементами могут быть сгруппированы в пары комплексно-сопряженных, именно с двумя членами пары, имеющими мнимые части, которые отличаются только знаком и та же самая настоящая часть. Если степень нечетная, то по теореме о промежуточном значении хотя бы один из корней является действительным. Следовательно, любая вещественная матрица нечетного порядка имеет по крайней мере одно действительное собственное значение, тогда как вещественная матрица четного порядка может не иметь никаких реальных собственных значений. Собственные векторы, связанные с этими комплексными собственными значениями, также являются комплексными и также входят в комплексно сопряженные пары.

Алгебраическая кратность

Пусть λ i является собственным значением матрицы A размером n на n. Алгебраическая кратность μA(λi) собственного значения - это его кратность как корень характеристического многочлена, то есть наибольшее целое число k такое, что (λ - λ i)делит равномерно этот многочлен.

Предположим, что матрица A имеет размерность n и d ≤ n различных собственных значений. В то время как уравнение (4) делит характеристический многочлен A на произведение n линейных членов с некоторыми потенциально повторяющимися членами, характеристический многочлен вместо этого может быть записан как произведение d членов, каждый из которых соответствует отличное собственное значение и возведенное в степень алгебраической кратности,

$|\; A\; -\; \lambda \; I\; |\; =\; (\lambda \; 1\; -\; \lambda )\; \mu \; A\; (\lambda \; 1)\; (\lambda \; 2\; -\; \lambda )\; \mu \; A\; (\lambda \; 2)\; \cdots \; (\lambda \; d\; -\; \lambda )\; \mu \; A\; (\lambda \; d),\; \{\backslash \; Displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; (\backslash \; lambda\; \_\; \{1\}\; -\; \backslash \; lambda)\; ^\; \{\backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{1\})\}\; (\backslash \; lambda\; \_\; \{2\}\; -\; \backslash \; lambda)\; ^\; \{\backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{2\})\}\; \backslash \; cdots\; (\backslash \; lambda\; \_\; \{d\}\; -\; \backslash \; lambda)\; ^\; \{\backslash \; mu\; \_\; \{A\}\; (\; \backslash \; lambda\; \_\; \{d\})\}.\}$

Есл и d = n, то правая часть является произведением n линейных членов, и это то же самое, что и в уравнении (4). Размер алгебраической кратности каждого собственного значения связан с размерностью n следующим образом:

$1\; \le \; \mu \; A\; (\lambda \; i)\; \le \; n,\; \mu \; A\; =\; \sum \; i\; =\; 1\; d\; \mu \; A\; (\lambda \; i)\; =\; n.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; 1\; \backslash \; leq\; \backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{i\})\; \backslash \; leq\; n,\; \backslash \backslash \backslash \; mu\; \_\; \{A\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; d\}\; \backslash \; mu\; \_\; \{A\}\; \backslash \; left\; (\backslash \; lambda\; \_\; \{i\}\; \backslash \; right)\; =\; n.\; \backslash \; end\; \{align\}\}\}$

Если μ A(λi) = 1, то λ i называется простым собственным значением. Если μ A(λi) равно геометрической кратности λ i, γ A(λi), определенной в следующем разделе, тогда λ i называется полупростым собственным значением.

Собственные подпространства, геометрическая кратность и собственный базис для матриц

Учитывая конкретное собственное значение λ матрицы A n x n, определите set E как все векторы v, которые удовлетворяют уравнению (2),

$E\; =\; \{v:\; (A\; -\; \lambda \; I)\; v\; =\; 0\}.\; \{\backslash \; displaystyle\; E\; =\; \backslash \; left\; \backslash \; \{\backslash \; mathbf\; \{v\}:\; (A-\; \backslash \; lambda\; I)\; \backslash \; mathbf\; \{v\}\; =\; 0\; \backslash \; right\; \backslash \}.\}$

С одной стороны, этот набор в точности соответствует ядро или нулевое пространство матрицы (A - λI). С другой стороны, по определению, любой ненулевой вектор, удовлетворяющий этому условию, является собственным вектором A, связанным с λ. Итак, множество E является объединением нулевого вектора с множеством всех собственных векторов A, связанных с λ, и E равно нулевому пространству (A - λI). E называется собственным подпространством или характеристическим пространством для A, связанного с λ. В общем случае λ - комплексное число, а собственные векторы представляют собой комплексные матрицы размером n на 1. Свойство нулевого пространства состоит в том, что это линейное подпространство , поэтому E является линейным подпространством в.

Поскольку собственное подпространство E является линейным подпространством, оно закрыто при сложении. То есть, если два вектора u и v принадлежат множеству E, записанному u, v ∈ E, то (u + v) ∈ E или, что то же самое, A (u + v) = λ (u + v). Это можно проверить, используя свойство распределения матричного умножения. Точно так же, поскольку E - линейное подпространство, оно замкнуто относительно скалярного умножения. То есть, если v ∈ E и α - комплексное число, (αv) ∈ E или, что то же самое, A (αv) = λ (αv). Это можно проверить, отметив, что умножение комплексных матриц на комплексные числа коммутативно. Пока u + v и αv не равны нулю, они также являются собственными векторами матрицы A, ассоциированной с λ.

Размерность собственного подпространства E, связанного с λ, или, что то же самое, максимальное количество линейно независимых собственных векторов, связанных с λ, называется геометрической кратностью γA(λ) собственного значения. Поскольку E также является нулевым пространством (A - λI), геометрическая кратность λ - это размерность нулевого пространства (A - λI), также называемая нулевым пространством (A - λI), которое относится к размерности и рангу (A - λI) как

$\gamma \; A\; (\lambda )\; =\; n\; -\; rank\; \; (A\; -\; \lambda \; I).\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\; =\; n-\; \backslash \; operatorname\; \{rank\}\; (A-\; \backslash \; lambda\; I).\}$

Из-за определения собственных значений и собственных векторов геометрическая кратность собственного значения должна быть не менее один, то есть каждое собственное значение имеет по крайней мере один связанный собственный вектор. Кроме того, геометрическая кратность собственного значения не может превышать его алгебраическую кратность. Кроме того, напомним, что алгебраическая кратность собственного значения не может превышать n.

$1\; \le \; \gamma \; A\; (\lambda )\; \le \; \mu \; A\; (\lambda )\; \le \; n\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\; \backslash \; leq\; \backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda)\; \backslash \; leq\; n\}$

Чтобы доказать неравенство $\gamma \; A\; (\lambda )\; \le \; \mu \; A\; (\lambda )\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\; \backslash \; leq\; \backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda)\}$, рассмотрите, как определение геометрической кратности подразумевает существование $\gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\}$ортонормированных собственных векторов $v\; 1,\dots ,\; V\; \gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{1\},\; \backslash ,\; \backslash \; ldots,\; \backslash ,\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{\backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\; \}\}$, такой что $A\; vk\; =\; \lambda \; vk\; \{\backslash \; displaystyle\; A\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{k\}\; =\; \backslash \; lambda\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{k\}\}$. Таким образом, мы можем найти (унитарную) матрицу $V\; \{\backslash \; displaystyle\; V\}$, у которой первый $\gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\}$столбцы являются этими собственными векторами, а оставшиеся столбцы могут быть любым ортонормированным набором из $n\; -\; \gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; n-\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\}$векторы, ортогональные этим собственным векторам $A\; \{\backslash \; displaystyle\; A\}$. Тогда $V\; \{\backslash \; displaystyle\; V\}$имеет полный ранг и поэтому является обратимым, и $AV\; =\; VD\; \{\backslash \; displaystyle\; AV\; =\; VD\}$с $D\; \{\; \backslash \; displaystyle\; D\}$матрица, верхний левый блок которой является диагональной матрицей $\lambda \; I\; \gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; \backslash \; lambda\; I\; \_\; \{\backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\}\}$. Это означает, что $(A\; -\; \xi \; I)\; V\; =\; V\; (D\; -\; \xi \; I)\; \{\backslash \; displaystyle\; (A-\; \backslash \; xi\; I)\; V\; =\; V\; (D-\; \backslash \; xi\; I)\}$. Другими словами, $A\; -\; \xi \; I\; \{\backslash \; displaystyle\; A-\; \backslash \; xi\; I\}$аналогично $D\; -\; \xi \; I\; \{\backslash \; displaystyle\; D-\; \backslash \; xi\; I\}$, из которого следует, что $det\; (A\; -\; \xi \; I)\; =\; det\; (D\; -\; \xi \; I)\; \{\backslash \; displaystyle\; \backslash \; det\; (A-\; \backslash \; xi\; I)\; =\; \backslash \; det\; (D-\; \backslash \; xi\; I)\}$. Но из определения $D\; \{\backslash \; displaystyle\; D\}$мы знаем, что $det\; (D\; -\; \xi \; I)\; \{\backslash \; displaystyle\; \backslash \; det\; (D-\; \backslash \; xi\; I)\}$содержит множитель $(\xi \; -\; \lambda )\; \gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; (\backslash \; xi\; -\; \backslash \; lambda)\; ^\; \{\backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\}\}$, который означает, что алгебраическая кратность $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$должна удовлетворять $\mu \; A\; (\lambda )\; \ge \; \gamma \; A\; (\lambda )\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda)\; \backslash \; geq\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda)\}$.

Предположим, что $A\; \{\backslash \; displaystyle\; A\}$имеет $d\; \le \; n\; \{\backslash \; displaystyle\; d\; \backslash \; leq\; n\}$различные собственные значения $\lambda \; 1,...,\; \lambda \; d\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\},...,\; \backslash \; lambda\; \_\; \{d\}\}$, где геометрическая кратность $\lambda \; i\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{i\}\; \}$- это $\gamma \; A\; (\lambda \; i)\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{i\})\}$. Общая геометрическая кратность $A\; \{\backslash \; displaystyle\; A\}$,

$\gamma \; A\; =\; \sum \; i\; =\; 1\; d\; \gamma \; A\; (\lambda \; i),\; d\; \le \; \gamma \; A\; \le \; n,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; gamma\; \_\; \{A\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{d\}\; \backslash \; gamma\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{i\}),\; \backslash \backslash \; d\; \backslash \; leq\; \backslash \; gamma\; \_\; \{A\}\; \backslash \; leq\; n,\; \backslash \; end\; \{align\}\}\}$

- размерность суммы всех собственных подпространств собственных значений $A\; \{\backslash \; displaystyle\; A\}$, или, что эквивалентно, максимальное количество линейно независимые собственные векторы $A\; \{\backslash \; displaystyle\; A\}$. Если $\gamma \; A\; =\; n\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{A\}\; =\; n\}$, то

• Прямая сумма собственных подпространств всех $A\; \{\backslash \; displaystyle\; A\}$- это все векторное пространство $C\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; ^\; \{n\}\}$.
• Основа $C\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; ^\; \{n\}\}$может быть сформировано из $n\; \{\backslash \; displaystyle\; n\}$линейно независимых собственных векторов $A\; \{\backslash \; displaystyle\; A\}$; такой базис называется собственным базисом
• . Любой вектор в $C\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; ^\; \{n\}\}$может быть записан как линейная комбинация собственных векторов $A\; \{\backslash \; displaystyle\; A\}$.

Дополнительные свойства собственных значений

Пусть $A\; \{\backslash \; displaystyle\; A\}$произвольное $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$матрица комплексных чисел с собственными значениями $\lambda \; 1,...,\; \lambda \; N\; \{\backslash \; Displaystyle\; \backslash \; lambda\; \_\; \{1\},...,\; \backslash \; lambda\; \_\; \{n\}\}$. Каждое собственное значение встречается $\mu \; A\; (\lambda \; i)\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{i\})\}$раз в этом списке, где $\mu \; A\; (\lambda \; i)\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{A\}\; (\backslash \; lambda\; \_\; \{i\})\}$- алгебраическая кратность собственного значения. Ниже приведены свойства этой матрицы и ее собственные значения:

• Трасса из $A\; \{\backslash \; displaystyle\; A\}$, определенная как сумма ее диагональных элементов, также сумма всех собственных значений,

  $tr\; \; (A)\; =\; \sum \; i\; =\; 1\; naii\; =\; \sum \; i\; =\; 1\; n\; \lambda \; i\; =\; \lambda \; 1\; +\; \lambda \; 2\; +\; \cdots \; +\; \lambda \; n.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{tr\}\; (A)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; a\_\; \{ii\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; lambda\; \_\; \{i\}\; =\; \backslash \; lambda\; \_\; \{1\}\; +\; \backslash \; lambda\; \_\; \{2\}\; +\; \backslash \; cdots\; +\; \backslash \; lambda\; \_\; \{n\}.\}$

• Определитель из $A\; \{\backslash \; displaystyle\; A\}$- произведение всех собственных значений,

  $det\; (A)\; =\; \prod \; i\; =\; 1\; n\; \lambda \; i\; =\; \lambda \; 1\; \lambda \; 2\; \cdots \; \lambda \; n.\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; lambda\; \_\; \{i\}\; =\; \backslash \; lambda\; \_\; \{1\}\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; cdots\; \backslash \; lambda\; \_\; \{n\}.\}$

• Собственные значения $k\; \{\backslash \; displaystyle\; k\}$степени $A\; \{\backslash \; displaystyle\; A\}$; т.е. собственные значения $A\; k\; \{\backslash \; displaystyle\; A\; ^\; \{k\}\}$для любого положительного целого числа $k\; \{\backslash \; displaystyle\; k\}$равны $\lambda \; 1\; k,...,\; \lambda \; nk\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\; ^\; \{k\},...,\; \backslash \; lambda\; \_\; \{n\}\; ^\; \{k\}\}$.
• Матрица $A\; \{\backslash \; displaystyle\; A\}$является обратимым тогда и только тогда, когда каждое собственное значение отлично от нуля.
• Если $A\; \{\backslash \; displaystyle\; A\}$обратимо, то собственные значения $A\; -\; 1\; \{\backslash \; displaystyle\; A\; ^\; \{-\; 1\}\}$равны $1\; \lambda \; 1,...,\; 1\; \lambda \; N\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\; \_\; \{1\}\}\},...,\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\; \_\; \{n\}\}\}\}$и геометрическая кратность каждого собственного значения совпадает. Более того, поскольку характеристический полином обратного преобразования является обратным полиномом оригинала, собственные значения имеют одинаковую алгебраическую кратность.
• Если $A\; \{\backslash \; displaystyle\; A\}$равно его сопряженному транспонированию $A\; \ast \; \{\backslash \; displaystyle\; A\; ^\; \{*\}\}$или эквивалентно, если $A\; \{\backslash \; displaystyle\; A\}$равно эрмитовскому, тогда каждое собственное значение вещественно. То же самое верно для любой симметричной вещественной матрицы.
• Если $A\; \{\backslash \; displaystyle\; A\}$не только эрмитовский, но и положительно-определенный, положительно-полуопределенный, отрицательно-определенный или отрицательно-полуопределенный, то каждое собственное значение будет соответственно положительным, неотрицательным, отрицательным или неположительным.
• Если $A\; \{\backslash \; displaystyle\; A\}$является унитарным, каждое собственное значение имеет абсолютное значение $|\; \lambda \; i\; |\; =\; 1\; \{\backslash \; displaystyle\; |\; \backslash \; lambda\; \_\; \{i\}\; |\; =\; 1\}$.
• , если $A\; \{\backslash \; displaystyle\; A\}$равно $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\; \}$матрица и $\{\lambda \; 1,\dots ,\; \lambda \; k\}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; lambda\; \_\; \{1\},\; \backslash \; ldots,\; \backslash \; lambda\; \_\; \{k\}\; \backslash \}\}$- ее собственные значения, тогда собственные значения матрицы $I\; +\; A\; \{\backslash \; displaystyle\; I\; +\; A\}$(где $I\; \{\backslash \; displaystyle\; I\}$- единичная матрица) равны $\{\lambda \; 1\; +\; 1,\dots ,\; \lambda \; k\; +\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; lambda\; \_\; \{1\}\; +1,\; \backslash \; ldots,\; \backslash \; lambda\; \_\; \{k\}\; +1\; \backslash \}\}$. Кроме того, если $\alpha \; \in \; C\; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; in\; \backslash \; mathbb\; \{C\}\}$, собственные значения $\alpha \; I\; +\; A\; \{\backslash \; displaystyle\; \backslash \; alpha\; I\; +\; A\}$равны $\{\lambda \; 1\; +\; \alpha ,\dots ,\; \lambda \; k\; +\; \alpha \}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; lambda\; \_\; \{1\}\; +\; \backslash \; alpha,\; \backslash \; ldots,\; \backslash \; lambda\; \_\; \{k\}\; +\; \backslash \; alpha\; \backslash \}\; \}$. В более общем смысле, для полинома $P\; \{\backslash \; displaystyle\; P\}$собственные значения матрицы $P\; (A)\; \{\backslash \; displaystyle\; P\; (A)\}$равны $\{P\; (\lambda \; 1),\dots ,\; P\; (\lambda \; K)\}\; \{\backslash \; displaystyle\; \backslash \; \{P\; (\backslash \; lambda\; \_\; \{1\}),\; \backslash \; ldots,\; P\; (\backslash \; lambda\; \_\; \{k\})\; \backslash \}\}$.

влево и правильные собственные векторы

Многие дисциплины традиционно представляют векторы как матрицы с одним столбцом, а не как матрицы с одной строкой. По этой причине слово «собственный вектор» в контексте матриц почти всегда относится к правому собственному вектору, а именно к вектору-столбцу, который умножает вправо $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$матрица $A\; \{\backslash \; displaystyle\; A\}$в определяющем уравнении, Equation (1),

$A\; v\; =\; \lambda \; v.\; \{\backslash \; displaystyle\; Av\; =\; \backslash \; lambda\; v.\}$

Задача на собственные значения и собственные векторы также может быть определена для векторов-строк, которые оставили матрицу умножения $A\; \{\backslash \; displaystyle\; A\}$. В этой формулировке определяющим уравнением является

$u\; A\; =\; \kappa \; u,\; \{\backslash \; displaystyle\; uA\; =\; \backslash \; kappa\; u,\}$

, где $\kappa \; \{\backslash \; displaystyle\; \backslash \; kappa\}$- скаляр и $u\; \{\backslash \; displaystyle\; u\}$представляет собой матрицу $1\; \times \; n\; \{\backslash \; displaystyle\; 1\; \backslash \; times\; n\}$. Любой вектор-строка $u\; \{\backslash \; displaystyle\; u\}$, удовлетворяющий этому уравнению, называется левым собственным вектором из $A\; \{\backslash \; displaystyle\; A\}$и $\kappa \; \{\backslash \; displaystyle\; \backslash \; kappa\}$- связанное с ним собственное значение. Транспонируя это уравнение,

$A\; T\; u\; T\; =\; \kappa \; u\; T.\; \{\backslash \; displaystyle\; A\; ^\; \{\backslash textf\; \{T\}\}\; u\; ^\; \{\backslash textf\; \{T\}\}\; =\; \backslash \; kappa\; u\; ^\; \{\backslash textf\; \{T\}\}.\}$

Сравнивая это уравнение с уравнением (1), оно сразу следует, что левый собственный вектор $A\; \{\backslash \; displaystyle\; A\}$совпадает с транспонированием правого собственного вектора $AT\; \{\backslash \; displaystyle\; A\; ^\; \{\backslash textf\; \{T\}\}\}$с тем же собственным значением. Furthermore, since the characteristic polynomial of $A\; T\; \{\backslash displaystyle\; A^\{\backslash textsf\; \{T\}\}\}$is the same as the characteristic polynomial of $A\; \{\backslash displaystyle\; A\}$, the eigenvalues of the left eigenvectors of $A\; \{\backslash displaystyle\; A\}$are the same as the eigenvalues of the right eigenvectors of $A\; T\; \{\backslash displaystyle\; A^\{\backslash textsf\; \{T\}\}\}$.

Diagonalization and the eigendecomposition

Suppose the eigenvectors of A form a basis, or equivalently A has n linearly independent eigenvectors v1, v2,..., vnwith associated eigenvalues λ1, λ2,..., λn. The eigenvalues need not be distinct. Define a square matrix Q whose columns are the n linearly independent eigenvectors of A,

$Q\; =\; [\; v\; 1\; v\; 2\; \cdots \; v\; n\; ].\; \{\backslash displaystyle\; Q=\{\backslash begin\{bmatrix\}v\_\{1\}v\_\{2\}\backslash cdots\; v\_\{n\}\backslash end\{bmatrix\}\}.\}$

Since each column of Q is an eigenvector of A, right multiplying A by Q scales each column of Q by its associated eigenvalue,

$A\; Q\; =\; [\; \lambda \; 1\; v\; 1\; \lambda \; 2\; v\; 2\; \cdots \; \lambda \; n\; v\; n\; ].\; \{\backslash displaystyle\; AQ=\{\backslash begin\{bmatrix\}\backslash lambda\; \_\{1\}v\_\{1\}\backslash lambda\; \_\{2\}v\_\{2\}\backslash cdots\; \backslash lambda\; \_\{n\}v\_\{n\}\backslash end\{bmatrix\}\}.\}$

With this in mind, define a diagonal matrix Λ where each diagonal element Λiiis th собственное значение, связанное с i-м столбцом Q. Тогда

$A\; Q\; =\; Q\; \Lambda .\; \{\backslash \; displaystyle\; AQ\; =\; Q\; \backslash \; Lambda.\}$

Поскольку столбцы Q линейно независимы, Q обратим. Умножив обе части уравнения справа на Q,

$A\; =\; Q\; \Lambda \; Q\; -\; 1,\; \{\backslash \; displaystyle\; A\; =\; Q\; \backslash \; Lambda\; Q\; ^\; \{-\; 1\},\}$

или вместо этого умножив обе части слева на Q,

$Q\; -\; 1\; AQ\; =\; \Lambda .\; \{\backslash \; displaystyle\; Q\; ^\; \{-\; 1\}\; AQ\; =\; \backslash \; Lambda.\}$

Таким образом, A можно разложить на матрицу, состоящую из его собственных векторов, диагональную матрицу с собственными значениями по диагонали и матрицу, обратную матрице собственных векторов. Это называется собственным разложением, и это преобразование подобия. Такая матрица A называется подобной диагональной матрице Λ или диагонализуемой. Матрица Q - это замена базовой матрицы преобразования подобия. По сути, матрицы A и Λ представляют собой одно и то же линейное преобразование, выраженное в двух разных базах. Собственные векторы используются в качестве основы при представлении линейного преобразования как Λ.

И наоборот, предположим, что матрица A диагонализуема. Пусть P - невырожденная квадратная матрица, такая что PAP - некоторая диагональная матрица D. Умножая оба слева на P, AP = PD. Следовательно, каждый столбец матрицы P должен быть собственным вектором матрицы A, собственное значение которого является соответствующим диагональным элементом матрицы D. Поскольку столбцы матрицы P должны быть линейно независимыми, чтобы P была обратимой, существует n линейно независимых собственных векторов матрицы A. Из этого следует, что собственные векторы матрицы A образуют базис тогда и только тогда, когда A диагонализуема.

Матрица, которая не диагонализируется, называется дефектной. Для дефектных матриц понятие собственных векторов обобщается до обобщенных собственных векторов, а диагональная матрица собственных значений обобщается до жордановой нормальной формы. Над алгебраически замкнутым полем любая матрица A имеет жорданову нормальную форму и поэтому допускает базис из обобщенных собственных векторов и разложение на обобщенные собственные подпространства.

Вариационная характеризация

В Эрмитов случай, собственным значениям можно дать вариационную характеристику. Наибольшее собственное значение $H\; \{\backslash \; displaystyle\; H\}$- это максимальное значение квадратичной формы $x\; TH\; x\; /\; x\; T\; x\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; textf\; \{T\}\}\; Hx\; /\; x\; ^\; \{\backslash textf\; \{T\}\}\; x\}$. Значение $x\; \{\backslash \; displaystyle\; x\}$, реализующее этот максимум, является собственным вектором.

Примеры матриц

Пример двумерной матрицы

Матрица преобразования A = $[2\; 1\; 1\; 2]\; \{\backslash \; displaystyle\; \{\backslash \; bigl\; [\}\; \{\backslash \; begin\; \{smallmatrix\}\; 2\; 1\; \backslash \backslash \; 1\; 2\; \backslash \; end\; \{smallmatrix\}\}\; \{\backslash \; bigr]\}\}$сохраняет направление фиолетовых векторов параллельно v λ = 1 = [1 −1] и синих векторов параллельно до v λ = 3 = [1 1]. Красные векторы не параллельны ни одному из собственных векторов, поэтому их направления изменяются преобразованием. Длины фиолетовых векторов не изменяются после преобразования (из-за их собственного значения 1), в то время как синие векторы в три раза больше длины оригинала (из-за их собственного значения 3). См. Также: Расширенная версия, показывающая все четыре квадранта.

Рассмотрим матрицу

$A\; =\; [2\; 1\; 1\; 2].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 1\; \backslash \backslash \; 1\; 2\; \backslash \; end\; \{bmatrix\}\}.\}$

На рисунке справа показано влияние этого преобразования на координаты точки на плоскости. Собственные параметры v этого преобразования соответствуют уравнению (1), а значения λ, для которых определитель матрицы (A - λI) равен нулю, являются собственными значениями.

Взяв определитель, чтобы найти характерный многочлен A,

$|\; A\; -\; \lambda \; I\; |\; =\; |\; [2\; 1\; 1\; 2]\; -\; \lambda \; [1\; 0\; 0\; 1]\; |\; =\; |\; 2\; -\; \lambda \; 1\; 1\; 2\; -\; \lambda \; |,\; Знак\; равно\; 3\; -\; 4\; \lambda \; +\; \lambda \; 2.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; |\; A-\; \backslash \; lambda\; I\; |\; =\; \backslash \; left\; |\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 1\; \backslash \backslash \; 1\; 2\; \backslash \; end\; \{bmatrix\}\}\; -\; \backslash \; lambda\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; right\; |\; =\; \{\backslash \; begin\; \{vmatrix\}\; 2-\; \backslash \; lambda\; 1\; \backslash \backslash \; 1\; 2-\; \backslash \; lambda\; \backslash \; end\; \{vmatrix\}\},\; \backslash \backslash \; [6pt]\; =\; 3-4\; \backslash \; lambda\; +\; \backslash \; lambda\; ^\; \{2\}.\; \backslash \; End\; \{align\}\}\}$

Если задан характерный полином равным нулю, он будет иметь корни при λ = 1 и λ = 3, которые являются двумя собственными значениями A.

Для λ = 1, уравнение ( 2) преобразуется в

$(A\; -\; I)\; v\; \lambda \; =\; 1\; =\; [1\; 1\; 1\; 1]\; [v\; 1\; v\; 2]\; =\; [0\; 0]\; \{\backslash \; displaystyle\; (AI)\; v\; \_\; \{\backslash \; lambda\; =\; 1\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 1\; \backslash \backslash \; 1\; 1\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \backslash \; v\_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\}\}$

$1\; v\; 1\; +\; 1\; v\; 2\; =\; 0\; \{\backslash \; displaystyle\; 1v\_\; \{1\}\; +\; 1v\_\; \{2\}\; =\; 0\}$; $1\; v\; 1\; +\; 1\; v\; 2\; =\; 0\; \{\backslash \; displaystyle\; 1v\_\; \{1\}\; +\; 1v\_\; \{2\}\; =\; 0\}$

Любой ненулевой вектор с v 1 = −v 2 решает это уравнение. Следовательно,

$v\; \lambda \; =\; 1\; =\; [v\; 1\; -\; v\; 1]\; =\; [1\; -\; 1]\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; =\; 1\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \backslash \; -\; v\_\; \{\; 1\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; -\; 1\; \backslash \; end\; \{bmatrix\}\}\}$

- собственный вектор A, соответствующий λ = 1, как и любое скалярное кратное этого вектора.

Для λ = 3 уравнение (2) становится

$(A\; -\; 3\; I)\; v\; \lambda \; =\; 3\; =\; [-\; 1\; 1\; 1\; -\; 1]\; [v\; 1\; v\; 2]\; =\; [0\; 0]\; \{\backslash \; displaystyle\; (A-3I)\; v\; \_\; \{\backslash \; lambda\; =\; 3\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; -1\; 1\; \backslash \backslash \; 1\; -1\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \; \backslash \; v\_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\}$

$-\; 1\; v\; 1\; +\; 1\; v\; 2\; =\; 0\; \{\backslash \; displaystyle\; -1v\_\; \{1\}\; +\; 1v\_\; \{2\}\; =\; 0\}$; $1\; v\; 1\; -\; 1\; v\; 2\; =\; 0\; \{\backslash \; displaystyle\; 1v\_\; \{1\}\; -1v\_\; \{2\}\; =\; 0\}$

Любой ненулевой вектор с v 1 = v 2 решает это уравнение. Следовательно,

$v\; \lambda \; =\; 3\; =\; [v\; 1\; v\; 1]\; =\; [1\; 1]\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; =\; 3\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \backslash \; v\_\; \{1\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\}\}$

является собственным вектором A, личным λ = 3, как и любое скалярное кратное этого вектора.

Таким образом, v λ = 1 и v λ = 3 являются собственными руками A, связанными с собственными значениями λ = 1 и λ = 3 соответственно.

Пример трехмерной матрицы

Рассмотрим матрицу

$A\; =\; [2\; 0\; 0\; 0\; 3\; 4\; 0\; 4\; 9].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 0\; 0\; \backslash \backslash \; 0\; 3\; 4\; \backslash \backslash \; 0\; 4\; 9\; \backslash \; end\; \{bmatrix\}\}.\}$

Характеристический многочлен A равен

$|\; A\; -\; \lambda \; I\; |\; =\; |\; [2\; 0\; 0\; 0\; 3\; 4\; 0\; 4\; 9]\; -\; \lambda \; [1\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 1]\; |\; =\; |\; 2\; -\; \lambda \; 0\; 0\; 0\; 3\; -\; \lambda \; 4\; 0\; 4\; 9\; -\; \lambda \; |,\; Знак\; равно\; (2\; -\; \lambda )\; [(3\; -\; \lambda )\; (9\; -\; \lambda )\; -\; 16]\; =\; -\; \lambda \; 3\; +\; 14\; \lambda \; 2\; -\; 35\; \lambda \; +\; 22.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; |\; A-\; \backslash \; lambda\; I\; |\; =\; \backslash \; left\; |\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 0\; 0\; \backslash \backslash \; 0\; 3\; 4\; \backslash \backslash \; 0\; 4\; 9\; \backslash \; end\; \{bmatrix\}\}\; -\; \backslash \; lambda\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; right\; |\; =\; \{\backslash \; begin\; \{vmatrix\}\; 2-\; \backslash \; lambda\; 0\; 0\; \backslash \backslash \; 0\; 3-\; \backslash \; lambda\; 4\; \backslash \backslash \; 0\; 4\; 9-\; \backslash \; lambda\; \backslash \; end\; \{vmatrix\}\},\; \backslash \backslash \; [6pt]\; =\; (\; 2-\; \backslash \; lambda)\; \{\backslash \; bigl\; [\}\; (3-\; \backslash \; lambda)\; (9-\; \backslash \; lambda)\; -16\; \{\backslash \; bigr]\}\; =\; -\; \backslash \; lambda\; ^\; \{3\}\; +14\; \backslash \; lambda\; ^\; \{2\}\; -35\; \backslash \; lambda\; +\; 22.\; \backslash \; End\; \{align\}\}\}$

Корнями характерного полинома являются 2, 1 и 11, которые являются единственными тремя собственными значениями A. Эти собственные значения соответствуют собственному состоянию $[1\; 0\; 0]\; T,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; textf\; \{T\}\},\}$$[0–2\; 1]\; T,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 0\; -2\; 1\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; textf\; \{T\}\},\}$и $[0\; 1\; 2]\; T\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 1\; 2\; \backslash \; end\; \{bmatrix\; \}\}\; ^\; \{\backslash \; textf\; \{T\}\}\}$или любое ненулевое кратное ему.

Пример трехмерной матрицы с комплексными собственными значениями

Рассмотрим матрицу циклической перестановки

$A\; =\; [0\; 1\; 0\; 0\; 0\; 1\; 1\; 0\; 0].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 1\; \backslash \backslash \; 1\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}.\}$

Эта матрица сдвигает координаты вектора вверх на одну позицию и перемещает первую координату вниз. Его характерный полином равен 1 - λ, корни которого равны

$\lambda \; 1\; =\; 1\; \lambda \; 2\; =\; -\; 1\; 2\; +\; i\; 3\; 2\; \lambda \; 3\; =\; \lambda \; 2\; \ast \; =\; -\; 1\; 2\; -\; i\; 3\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнены\; \}\; \backslash \; lambda\; \_\; \{1\}\; =\; 1\; \backslash \backslash \backslash \; lambda\; \_\; \{2\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; +\; \backslash \; mathbf\; \{i\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{3\}\}\; \{2\}\; \}\; \backslash \backslash \backslash \; lambda\; \_\; \{3\}\; =\; \backslash \; lambda\; \_\; \{2\}\; ^\; \{*\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; -\; \backslash \; mathbf\; \{i\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{3\}\}\; \{\; 2\}\}\; \backslash \; end\; \{align\}\}\}$

где $i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{i\}\}$- мнимая единица с $i\; 2\; =\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{i\}\; ^\; \{2\}\; =\; -\; 1.\}$

Для действующего собственного значения λ 1 = 1 вектор любой с тремя равными ненулевыми элементами является собственным вектором. Например,

$A\; [5\; 5\; 5]\; =\; [5\; 5\; 5]\; =\; 1\; \cdot \; [5\; 5\; 5].\; \{\backslash \; Displaystyle\; A\; \{\backslash \; begin\; \{bmatrix\}\; 5\; \backslash \backslash \; 5\; \backslash \backslash \; 5\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 5\; \backslash \; 5\; \backslash \backslash \; 5\; \backslash \; end\; \{bmatrix\}\}\; =\; 1\; \backslash \; cdot\; \{\backslash \; begin\; \{\; bmatrix\}\; 5\; \backslash \backslash \; 5\; \backslash \backslash \; 5\; \backslash \; end\; \{bmatrix\}\}.\}$

Для комплексно сопряженной пары мнимых собственных значений

$\lambda \; 2\; \lambda \; 3\; =\; 1,\; \lambda \; 2\; 2\; =\; \lambda \; 3,\; \lambda \; 3\; 2\; =\; \lambda \; 2.\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; lambda\; \_\; \{3\}\; =\; 1,\; \backslash \; quad\; \backslash \; lambda\; \_\; \{2\}\; ^\; \{2\}\; =\; \backslash \; lambda\; \_\; \{3\},\; \backslash \; quad\; \backslash \; lambda\; \_\; \{3\}\; ^\; \{2\; \}\; =\; \backslash \; lambda\; \_\; \{2\}.\}$

Тогда

$A\; [1\; \lambda \; 2\; \lambda \; 3]\; =\; [\lambda \; 2\; \lambda \; 3\; 1]\; =\; \lambda \; 2\; \cdot \; [1\; \lambda \; 2\; \lambda \; 3],\; \{\backslash \; displaystyle\; A\; \{\; \backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \backslash \; lambda\; \_\; \{2\}\; \backslash \backslash \backslash \; lambda\; \_\; \{3\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; lambda\; \_\; \{2\}\; \backslash \backslash \backslash \; lambda\; \_\; \{3\}\; \backslash \; \backslash \; 1\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; cdot\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \backslash \; lambda\; \_\; \{2\}\; \backslash \backslash \backslash \; lambda\; \_\; \{3\}\; \backslash \; end\; \{bmatrix\}\},\}$

и

$A\; [1\; \lambda \; 3\; \lambda \; 2]\; =\; [\lambda \; 3\; \lambda \; 2\; 1]\; =\; \lambda \; 3\; \cdot \; [1\; \lambda \; 3\; \lambda \; 2].\; \{\backslash \; displaystyle\; A\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \backslash \; lambda\; \_\; \{3\}\; \backslash \backslash \backslash \; lambda\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; lambda\; \_\; \{3\}\; \backslash \backslash \backslash \; lambda\; \_\; \{2\}\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; lambda\; \_\; \{3\}\; \backslash \; cdot\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \backslash \; lambda\; \_\; \{3\}\; \backslash \backslash \backslash \; lambda\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\; \}.\}$

Следовательно, два других устройства являются равными $v\; \lambda \; 2\; =\; [1\; \lambda \; 2\; \lambda \; 3]\; T\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; \_\; \{2\}\}\; =\; \{\backslash \; begin\; \{\; bmatrix\}\; 1\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; lambda\; \_\; \{3\}\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; textf\; \{T\}\}\}$и $v\; \lambda \; 3\; =\; [1\; \lambda \; 3\; \lambda \; 2]\; T\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; \_\; \{3\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \; lambda\; \_\; \{3\}\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; textf\; \{\; T\}\}\}$с собственными значениями λ 2 и λ 3 соответственно. Два комплексных сопроводительных изображения включают в себя комплексноряженную пару,

$v\; \lambda \; 2\; =\; v\; \lambda \; 3\; \ast .\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; \_\; \{2\}\}\; =\; v\; \_\; \{\backslash \; lambda\; \_\; \{3\}\}\; ^\; \{*\}.\}$

Пример диагональной матрицы

Матрицы с элементами только по главной диагонали называются диагональные матрицы. Собственные значения диагональной матрицы - это сами диагональные элементы. Рассмотрим матрицу

$A\; =\; [1\; 0\; 0\; 0\; 2\; 0\; 0\; 0\; 3].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 0\; 2\; 0\; \backslash \backslash \; 0\; 0\; 3\; \backslash \; end\; \{bmatrix\}\}.\}$

Характеристический многочлен A равен

$|\; A\; -\; \lambda \; I\; |\; Знак\; равно\; (1\; -\; \lambda )\; (2\; -\; \lambda )\; (3\; -\; \lambda ),\; \{\backslash \; displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; (1-\; \backslash \; lambda)\; (2-\; \backslash \; lambda)\; (3-\; \backslash \; lambda),\}$

который имеет корни λ 1 = 1, λ 2 = 2 и λ 3 = 3. Эти корни являются диагональными элементами, а также собственными значениями A.

Каждый диагональный элемент соответствует собственному вектору, единственный компонент которого находится в той же строке, что и этот диагональный элемент. В этой системе собственные значения соответствуют собственное устройством:

$v\; \lambda \; 1\; =\; [1\; 0\; 0],\; v\; \lambda \; 2\; =\; [0\; 1\; 0],\; v\; \lambda \; 3\; =\; [0\; 0\; 1],\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; лямбда\; \_\; \{1\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\},\; \backslash \; quad\; v\; \_\; \{\backslash \; lambda\; \_\; \{2\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \; \backslash \; 0\; \backslash \; end\; \{bmatrix\}\},\; \backslash \; quad\; v\; \_\; \{\backslash \; lambda\; \_\; \{3\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\},\}$

соответственно, а также скалярные кратные этих векторов.

Пример треугольной матрицы

Матрица, все элементы которой выше главной диагонали равны нулю, называется нижней треугольной матрицей, а матрица, элементы которой ниже главной диагонали - все нуль называется верхнетреугольной матрицей. Как и в собственных случаях диагональных матриц, значения треугольных матриц являются элементами главной диагонали.

Рассмотрим нижнюю треугольную матрицу,

$A\; =\; [1\; 0\; 0\; 1\; 2\; 0\; 2\; 3\; 3].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 1\; 2\; 0\; \backslash \backslash \; 2\; 3\; 3\; \backslash \; end\; \{bmatrix\}\}.\}$

Характеристический многочлен A равен

$|\; A\; -\; \lambda \; I\; |\; Знак\; равно\; (1\; -\; \lambda )\; (2\; -\; \lambda )\; (3\; -\; \lambda ),\; \{\backslash \; displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; (1-\; \backslash \; lambda)\; (2-\; \backslash \; lambda)\; (3-\; \backslash \; lambda),\}$

который имеет корни λ 1 = 1, λ 2 = 2 и λ 3 = 3. Эти корни являются диагональными элементами, а также собственными значениями A.

Эти собственные значения соответствуют современному состоянию,

$v\; \lambda \; 1\; =\; [1\; -\; 1\; 1\; 2],\; v\; \lambda \; 2\; знак\; равно\; [0\; 1\; -\; 3],\; v\; \lambda \; 3\; =\; [0\; 0\; 1],\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; lambda\; \_\; \{1\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; -\; 1\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; конец\; \{bmatrix\}\},\; \backslash \; quad\; v\; \_\; \{\backslash \; lambda\; \_\; \{2\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; -\; 3\; \backslash \; end\; \{bmatrix\}\},\; \backslash \; quad\; v\; \_\; \{\backslash \; lambda\; \_\; \{3\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\},\}$

соответственно, а также скалярные кратные этих векторов.

Пример матрицы с повторяющимися собственными значениями

Как и в примере нижняя треугольная матрица

$A\; =\; [2\; 0\; 0\; 0\; 1\; 2\; 0\; 0\; 0\; 1\; 3\; 0\; 0\; 0\; 1\; 3],\; \{\backslash \; Displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 2\; 0\; 0\; 0\; \backslash \backslash \; 1\; 2\; 0\; 0\; \backslash \backslash \; 0\; 1\; 3\; 0\; \backslash \backslash \; 0\; 0\; 1\; 3\; \backslash \; end\; \{bmatrix\; \}\},\}$

имеет характерный многочлен, является произведением его диагональных элементов,

$|\; A\; -\; \lambda \; I\; |\; =\; |\; 2\; -\; \lambda \; 0\; 0\; 0\; 1\; 2\; -\; \lambda \; 0\; 0\; 0\; 1\; 3\; -\; \lambda \; 0\; 0\; 0\; 1\; 3\; -\; \lambda \; |\; Знак\; равно\; (2\; -\; \lambda )\; 2\; (3\; -\; \lambda )\; 2.\; \{\backslash \; displaystyle\; |\; A-\; \backslash \; lambda\; I\; |\; =\; \{\backslash \; begin\; \{vmatrix\}\; 2-\; \backslash \; lambda\; 0\; 0\; 0\; \backslash \backslash \; 1\; 2-\; \backslash \; lambda\; 0\; 0\; \backslash \backslash \; 0\; 1\; 3-\; \backslash \; lambda\; 0\; \backslash \backslash \; 0\; 0\; 1\; 3\; -\; \backslash \; lambda\; \backslash \; end\; \{vmatrix\}\}\; =\; (2-\; \backslash \; lambda)\; ^\; \{2\}\; (3-\; \backslash \; lambda)\; ^\; \{2\}.\}$

Корни этого многочлена, а следовательно, и собственные значения, равны 2 и 3. Алгебраическая кратность каждого собственного значения равна 2; Словами они оба являются двойными корнями. Сумма алгебраических кратностей всех различных величин равна μ A = 4 = n, порядок характерного многочлена и размерность A.

С другой стороны, геометрическая кратность собственного значения 2 равно 1, потому что его собственное подпространство распространяется только на один вектор $[0\; 1\; -\; 1\; 1]\; T\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 1\; -1\; 1\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; textf\; \{T\}\}\}$и поэтому является одномерным. Точно так же геометрическая кратность собственного значения 3 равна 1, потому что его собственное подпространство распространяется только на один вектор $[0\; 0\; 0\; 1]\; T\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 0\; 0\; 1\; \backslash \; end\; \{bmatrix\; \}\}\; ^\; \{\backslash \; textf\; \{T\}\}\}$. Полная геометрическая кратность γ A равна 2, что является наименьшим возможным значением для матрицы с двумя собственными значениями. Геометрические характеристики нового в новом разделе.

Тождество собственного вектора и собственного значения

Для эрмитовой матрицы квадрат нормы j-го компонента нормализованного собственного вектора может быть вычислен с использованием только собственных значений матрицы и собственных соответствующих вспомогательная матрица,

$|\; v\; i,\; j\; |\; 2\; знака\; равно\; \prod \; К\; (\lambda \; я\; -\; \lambda \; К\; (М\; J))\; \prod \; К\; \ne \; я\; (\lambda \; я\; -\; \lambda \; К),\; \{\backslash \; Displaystyle\; |\; v\_\; \{я,\; j\}\; |\; ^\; \{2\}\; =\; \{\backslash \; гидроразрыва\; \{\backslash \; prod\; \_\; \{k\}\; \{(\backslash \; lambda\; \_\; \{i\}\; -\; \backslash \; lambda\; \_\; \{k\}\; (M\_\; \{j\}))\}\}\; \{\backslash \; prod\; \_\; \{k\; \backslash \; neq\; i\}\; \{\; (\backslash \; lambda\; \_\; \{i\}\; -\; \backslash \; lambda\; \_\; \{k\})\}\}\},\}$где $M\; j\; \{\backslash \; textstyle\; M\_\; \{j\}\}$- это подматрица, образованная удалением j-й строки и столбца из исходная матрица.

Собственные значения и собственные функции дифференциальных операторов

Определенные значения и собственные векторы линейного преобразования T остаются в силе, даже если лежащее в основе собственного пространства бесконечномерным Гильбертом или Банахово пространство. Широко используемым классом линейных преобразований, действующих в бесконечных пространствах, являются дифференциальные операторы в функциональных пространствах. Пусть D - линейный действующий оператор в бесконечно дифференцируемых вещественных функций аргумента t. Уравнение на собственные значения для D - это дифференциальное уравнение

$D\; f\; (t)\; =\; \lambda \; f\; (t)\; \{\backslash \; displaystyle\; Df\; (t)\; =\; \backslash \; lambda\; f\; (t)\}$

Функции, которые удовлетворяют этим уравнением являются собственными устройствами D и обычно называются собственными функциями .

Пример оператора производной

Рассмотрим оператор производной $ddt\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{d\}\; \{dt\}\}\}$с уравнением для собственных значений

$ddtf\; (t)\; =\; \lambda \; f\; (t).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; f\; (t)\; =\; \backslash \; lambda\; f\; (t).\}$

Это дифференциальное уравнение можно решить, умножив обе части на dt / f (t) и интегрировав. Его решение, экспоненциальная функция

$f\; (t)\; =\; f\; (0)\; e\; \lambda \; t,\; \{\backslash \; displaystyle\; f\; (t)\; =\; f\; (0)\; e\; ^\; \{\backslash \; lambda\; t\},\}$

, собственная функция производного оператора. В этом случае собственная функция сама функция является функцией связанного с ней собственного значения. В частности, при λ = 0 собственная функция f (t) является постоянной.

В основной статье собственная функция приводятся другие примеры.

Общее определение

Концепция собственных и собственных векторов естественным образом распространяется на произвольные линейные преобразования в произвольных векторных пространствах. Пусть V - новое пространство над некоторыми полем K из скаляров, и пусть T - линейное преобразование, отображающее V в V,

$T:\; V\; \to \; V.\; \{\backslash \; displaystyle\; T\; :\; V\; \backslash \; to\; V.\}$

Мы говорим, что ненулевой вектор v ∈ V собственный вектор вектор T тогда и только тогда, когда существует скаляр λ ∈ K такое, что

$T\; (v)\; =\; \lambda \; v.\; \{\backslash \; Displaystyle\; T\; (\backslash \; mathbf\; \{v\})\; =\; \backslash \; lambda\; \backslash \; mathbf\; \{v\}.\}$

(5)

Это уравнение называется уравнением собственных значений для T, а скаляр λ - это собственное значение Т, соответствующему собственному вектору v . T (v ) - это результат преобразования T к вектору v, а λ v - произведение скаляра λ с v.

собственными подпространствами, геометрическая кратность и собственное базис

Для собственного значения λ рассмотрим множество

$E\; =\; \{v:\; T\; (v)\; =\; \lambda \; v\},\; \{\backslash \; displaystyle\; E\; =\; \backslash \; left\; \backslash \; \{\backslash \; mathbf\; \{v\}:\; T\; (\backslash \; mathbf\; \{\; v\})\; =\; \backslash \; lambda\; \backslash \; mathbf\; \{v\}\; \backslash \; right\; \backslash \},\}$

который является объединением нулевого вектора с набором всех собственных векторов, связанных с λ. E называется собственным подпространством или характеристическим пространством T, с λ.

По определению линейного преобразования

$T\; (x\; +\; y)\; =\; T\; (x)\; +\; T\; (y),\; T\; (\alpha \; x)\; =\; \alpha \; T\; (x),\; \{\backslash \; displaystyle\; \{\backslash \; начало\; \{выровнено)\; \}\; T\; (\backslash \; mathbf\; \{x\}\; +\; \backslash \; mathbf\; \{y\})\; =\; T\; (\backslash \; mathbf\; \{x\})\; +\; T\; (\backslash \; mathbf\; \{y\}),\; \backslash \backslash \; T\; (\backslash \; alpha\; \backslash \; mathbf\; \{x\})\; =\; \backslash \; альфа\; T\; (\backslash \; mathbf\; \{x\}),\; \backslash \; end\; \{align\}\}\}$

для (x,y) ∈ V и α ∈ K. Следовательно, если u и v - собственные конструкции T, связанные с числом значений λ, а именно u,v∈ E,

$T\; (u\; +\; v)\; =\; \lambda \; (u\; +\; v),\; T\; (\alpha \; v)\; =\; \lambda \; (\alpha \; v).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; T\; (\backslash \; mathbf\; \{u\}\; +\; \backslash \; mathbf\; \{v\})\; =\; \backslash \; lambda\; (\backslash \; mathbf\; \{u\}\; +\; \backslash \; mathbf\; \{v\}),\; \backslash \backslash \; T\; (\backslash \; alpha\; \backslash \; mathbf\; \{\; v\})\; =\; \backslash \; lambda\; (\backslash \; alpha\; \backslash \; mathbf\; \{v\}).\; \backslash \; end\; \{align\}\}\}$

Итак, и u+ v, и α v являются либо нулевыми, либо собственными деревьями T, связанными с λ, а именно u+ v, α v ∈ E, а E замкнуто относительно сложения и скалярного умножения. Собственное подпространство E, связанное с λ, поэтому является линейным подпространством V. Если это подпространство имеет размерность 1, его иногда называют собственной линией .

. Геометрическая кратность γT(λ) собственного значения λ равна размерность собственного подпространства, связанного с λ, т. е. максимальное количество линейно независимых векторов, связанных с этим значением длины. По определению собственных значений и векторов γ T (λ) ≥ 1, потому что каждое собственное значение имеет по крайней мере один вектор.

Собственные подпространства T всегда образуют прямую сумму. Как следствие, собственные исходные значения всегда линейно независимы. Следовательно, сумма размеров собственных подпространств не может быть более n различных значений, в которых работает T, и не может быть более n различных значений.

Любое подпространство, натянутое на собственном T, является инвариантное подпространство в T, и ограничение T на такое подпространство диагонализуемо. Более, если все внутреннее пространство V может быть покрыто собственными объектами T, или, что то же самое, если прямая сумма собственных подпространств, связанных со всеми собственными значениями T, является всем векторным пространством V, то базис V называется eigenbasis может быть сформирован из линейно базовых собственных векторов T. Когда допускает собственный диагонализуем.

Нулевой вектор как собственный вектор

Хотя определение этого вектора используется в статье, исключает нулевой вектор, можно определить собственные значения и гибридного вектора, чтобы нулевой вектор был собственный вектором.

Рассмотрим снова уравнение собственных значений, Equation (5). Определим собственное значение как любой скаляр λ ∈ K такой, что существует ненулевой вектор v ∈ V, удовлетворяющий уравнению (5). Важно, чтобы в этой версии собственного определения значения указывается, что вектор не равен нулю, иначе по этому определению нулевой вектор позволит любому скаляру в K быть значения положения. Определите собственный v, связанный с определенным значением λ, как любой вектор, который при заданном λ удовлетворяет уравнению (5). Учитывая собственное значение, нулевой вектор входит в число векторов, удовлетворяющих уравнению (5), поэтому нулевой вектор включается в число собственных векторов этим альтернативным определением.

Спектральная теория

Если λ является собственным значением T, то оператор (T - λI) не взаимно однозначен, и поэтому его обратный (T - λI) не существует. Обратное верно для конечных векторных пространств, но не для бесконечномерных векторных пространств. В общем случае оператор (T - λI) может не иметь обратного, даже если λ не является собственным значением.

По этой причине в функциональном анализе собственные значения могут быть обобщены на спектр линейного оператора T как набор всех скаляров λ, для которых оператор (T - λI) не имеет ограниченного обратного. Спектр оператора всегда содержит все его собственные значения, но не ограничивается ими.

Ассоциативные алгебры и теория представлений

Можно обобщить алгебраический объект, действующий в векторном пространстве, заменив единственный оператор, действующий в векторном пространстве, представлением алгебры - ассоциативная алгебра, действующая на модуль. Изучение таких действий является областью теории представлений.

теоретико-репрезентативная концепция веса является аналогом собственных значений, а весовые векторы и весовые пространства являются аналогами собственных векторов и собственных подпространств, соответственно.

Динамические уравнения

Простейшие разностные уравнения имеют вид

$x\; t\; =\; a\; 1\; x\; t\; -\; 1\; +\; a\; 2\; x\; t\; -\; 2\; +\; \cdots \; +\; a\; k\; x\; t\; -\; k.\; \{\backslash \; displaystyle\; x\_\; \{t\}\; =\; a\_\; \{1\}\; x\_\; \{t-1\}\; +\; a\_\; \{2\}\; x\_\; \{t-2\}\; +\; \backslash \; cdots\; +\; a\_\; \{k\}\; x\_\; \{tk\}.\}$

Решение этого уравнение для x через t находится с помощью его характеристического уравнения

$\lambda \; k\; -\; a\; 1\; \lambda \; k\; -\; 1\; -\; a\; 2\; \lambda \; k\; -\; 2\; -\; \cdots \; -\; ak\; -\; 1\; \lambda \; -\; ak\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{k\}\; -a\_\; \{1\}\; \backslash \; lambda\; ^\; \{k-1\}\; -a\_\; \{2\}\; \backslash \; lambda\; ^\; \{k-2\}\; -\; \backslash \; cdots\; -a\_\; \{k-1\}\; \backslash \; lambda\; -a\_\; \{k\}\; =\; 0,\; \}$

, которые можно найти путем сложения в матрицу, образуют набор уравнений, состоящий из приведенного выше разностного уравнения и k - 1 уравнений $xt\; -\; 1\; =\; xt\; -\; 1,\dots ,\; xt\; -\; k\; +\; 1\; =\; xt\; -\; к\; +\; 1,\; \{\backslash \; displaystyle\; x\_\; \{t-1\}\; =\; x\_\; \{t-1\},\; \backslash \; \backslash \; dots,\; \backslash \; x\_\; \{t-k\; +\; 1\}\; =\; x\_\; \{t-k\; +\; 1\},\}$получение k-мерной системы первого порядка в векторе сгруппированных переменных $[xt\; \cdots \; xt\; -\; k\; +\; 1]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; x\_\; \{t\}\; \backslash \; cdots\; x\_\; \{t-k\; +\; 1\}\; \backslash \; end\; \{bmatrix\}\}\}$в терминах его однократно запаздывающего значения и взятия характеристического уравнения матрицы этой системы. Это уравнение дает k характеристических корней $\lambda \; 1,\dots ,\; \lambda \; k,\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\},\; \backslash ,\; \backslash \; ldots,\; \backslash ,\; \backslash \; lambda\; \_\; \{k\},\}$для использования в решении уравнения

$xt\; =\; c\; 1\; \lambda \; 1\; t\; +\; \cdots \; +\; ck\; \lambda \; kt.\; \{\backslash \; displaystyle\; x\_\; \{t\}\; =\; c\_\; \{1\}\; \backslash \; lambda\; \_\; \{1\}\; ^\; \{t\}\; +\; \backslash \; cdots\; +\; c\_\; \{k\}\; \backslash \; lambda\; \_\; \{k\}\; ^\; \{t\}.\}$

Используется аналогичная процедура для решения дифференциального уравнения вида

$dkxdtk\; +\; ak\; -\; 1\; dk\; -\; 1\; xdtk\; -\; 1\; +\; \cdots \; +\; a\; 1\; dxdt\; +\; a\; 0\; x\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{k\}\; x\}\; \{dt\; ^\; \{k\}\}\}\; +\; a\_\; \{k-1\}\; \{\backslash \; frac\; \{d\; ^\; \{k-1\}\; x\}\; \{dt\; ^\; \{k-1\}\}\}\; +\; \backslash \; cdots\; +\; a\_\; \{1\; \}\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; +\; a\_\; \{0\}\; x\; =\; 0.\}$

Вычисление

Вычисление собственных значений и собственных векторов - это тема, где теория представлена ​​в учебниках элементарной линейной алгебры, часто очень далеко от практики.

Классический метод

Классический метод заключается в том, чтобы сначала найти собственные значения, а затем вычислить собственные векторы для каждого собственного значения. В некоторых отношениях он плохо подходит для неточной арифметики, такой как с плавающей запятой.

Собственные значения

Собственные значения матрицы $A\; \{\backslash \; displaystyle\; A\}$можно определить, найдя корни характеристического многочлена. Это легко для матриц $2\; \times \; 2\; \{\backslash \; displaystyle\; 2\; \backslash \; times\; 2\}$, но сложность быстро возрастает с увеличением размера матрицы.

Теоретически коэффициенты характеристического полинома можно вычислить точно, поскольку они являются суммами произведений элементов матрицы; и есть алгоритмы, которые могут найти все корни многочлена произвольной степени с любой требуемой точностью. Однако на практике этот подход нежизнеспособен, поскольку коэффициенты могут быть загрязнены неизбежными ошибками округления, а корни полинома могут быть чрезвычайно чувствительной функцией коэффициентов (как показано на примере Полином Уилкинсона ). Даже для матриц, элементы которых являются целыми числами, вычисление становится нетривиальным, поскольку суммы очень велики; постоянный член - это определитель , который для $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$представляет собой сумму $n!\; \{\backslash \; displaystyle\; n!\}$различных продуктов.

Явные алгебраические формулы для корней многочлена существуют только в том случае, если степень $n\; \{\backslash \; displaystyle\; n\}$- 4 или меньше. Согласно теореме Абеля – Руффини не существует общей, явной и точной алгебраической формулы для корней многочлена степени 5 или выше. (Общность имеет значение, потому что любой многочлен со степенью $n\; \{\backslash \; displaystyle\; n\}$является характеристическим многочленом некоторой сопутствующей матрицы порядка $n\; \{\backslash \; displaystyle\; n\}$.) Следовательно, для матриц порядка 5 или более собственные значения и собственные векторы не могут быть получены с помощью явной алгебраической формулы и, следовательно, должны вычисляться приближенными численными методами. Даже точная формула для корней многочлена 3-й степени нецелесообразна в числовом отношении.

Собственные векторы

После того, как известно (точное) значение собственного значения, соответствующие собственные векторы могут быть найдены путем нахождения ненулевых решений уравнения для собственных значений, которое становится системой линейных уравнений с известными коэффициентами. Например, если известно, что 6 является собственным значением матрицы

$A\; =\; [4\; 1\; 6\; 3]\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; 4\; 1\; \backslash \backslash \; 6\; 3\; \backslash \; end\; \{bmatrix\}\}\}$

мы можем найти его собственные векторы, решив уравнение $A\; v\; =\; 6\; v\; \{\backslash \; displaystyle\; Av\; =\; 6v\}$, то есть

$[4\; 1\; 6\; 3]\; [xy]\; =\; 6\; \cdot \; [\; ху]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 4\; 1\; \backslash \backslash \; 6\; 3\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; x\; \backslash \backslash \; y\; \backslash \; end\; \{bmatrix\}\}\; =\; 6\; \backslash \; cdot\; \{\backslash \; begin\; \{bmatrix\}\; x\; \backslash \backslash \; y\; \backslash \; end\; \{bmatrix\}\}\}$

Это матричное уравнение эквивалентно двум линейным уравнениям

$\{4\; x\; +\; y\; =\; 6\; x\; 6\; x\; +\; 3\; y\; =\; 6\; y\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\; \backslash \; begin\; \{align\}\; 4x\; +\; y\; =\; 6x\; \backslash \backslash \; 6x\; +\; 3y\; =\; 6y\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$то есть $\{-\; 2\; x\; +\; y\; =\; 0\; 6\; x\; -\; 3\; y\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; -2x\; +\; y\; =\; 0\; \backslash \backslash \; 6x-3y\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Оба уравнения сводятся к одному линейному уравнению $y\; =\; 2\; x\; \{\backslash \; displaystyle\; y\; =\; 2x\}$. Следовательно, любой вектор формы $[a\; 2\; a]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; a\; \backslash \backslash \; 2a\; \backslash \; end\; \{bmatrix\}\}\}$для любого ненулевого действительного числа $a\; \{\backslash \; displaystyle\; a\}$, является собственным вектором $A\; \{\backslash \; displaystyle\; A\}$с собственным значением $\lambda \; =\; 6\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; 6\}$.

Матрица $A\; \{\backslash \; displaystyle\; A\}$выше имеет другое собственное значение $\lambda \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; 1\}$. Аналогичный расчет показывает, что соответствующие собственные векторы являются ненулевыми решениями $3\; x\; +\; y\; =\; 0\; \{\backslash \; displaystyle\; 3x\; +\; y\; =\; 0\}$, то есть любого вектора вида $[\; b\; -\; 3\; b]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; b\; \backslash \backslash \; -\; 3b\; \backslash \; end\; \{bmatrix\}\}\}$, для любого ненулевого действительного числа $b\; \{\backslash \; displaystyle\; b\}$.

Простые итерационные методы

Обратный подход, в котором сначала ищут собственные векторы, а затем определяют каждое собственное значение по собственному вектору, оказывается гораздо более приемлемым для компьютеров. Самый простой алгоритм здесь состоит из выбора произвольного начального вектора и последующего многократного умножения его на матрицу (при необходимости нормализация вектора для сохранения его элементов разумного размера); это заставляет вектор сходиться к собственному вектору. Вариант заключается в умножении вектора на $(A\; -\; \mu \; I)\; -\; 1\; \{\backslash \; displaystyle\; (A-\; \backslash \; mu\; I)\; ^\; \{-\; 1\}\}$; это приводит к тому, что он сходится к собственному вектору собственного значения, ближайшего к $\mu \; \in \; C\; \{\backslash \; displaystyle\; \backslash \; mu\; \backslash \; in\; \backslash \; mathbb\; \{C\}\}$.

If $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$является (хорошее приближение) собственным вектором $A\; \{\backslash \; displaystyle\; A\}$, тогда соответствующее собственное значение может быть вычислено как

$\lambda \; =\; v\; \ast \; A\; vv\; \ast \; v\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{v\}\; ^\; \{*\}\; A\; \backslash \; mathbf\; \{v\}\}\; \{\backslash \; mathbf\; \{v\}\; ^\; \{*\}\; \backslash \; mathbf\; \{v\}\}\}\}$

где $v\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; ^\; \{*\}\}$обозначает сопряженное транспонирование из $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$.

Modern методы

Эффективные и точные методы вычисления собственных значений и собственных векторов произвольных матриц не были известны до тех пор, пока в 1961 году не был разработан QR-алгоритм. Объединение преобразования Хаусхолдера с LU разложение приводит к алгоритму с лучшей сходимостью, чем алгоритм QR. Для больших эрмитовых разреженных матриц, алгоритм Ланцоша является одним из примеров эффективного итерационного метода для вычисления собственных значений и собственных векторов, среди нескольких других возможностей.

Большинство числовых методов, которые вычисляют собственные значения матрицы, также определяют набор соответствующих собственных векторов как побочный продукт вычисления, хотя иногда разработчики предпочитают отбрасывать информацию о собственном векторе, как только она перестает быть необходимо.

Приложения

Собственные значения геометрических преобразований

В следующей таблице представлены некоторые примеры преобразований на плоскости вместе с их матрицами 2 × 2, собственными значениями и собственными векторами.

	Масштабирование	Неравномерное масштабирование	Вращение	Горизонтальный сдвиг	Гиперболическое вращение
Иллюстрация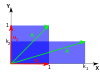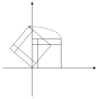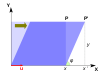
Матрица	$[k\; 0\; 0\; k]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; k\; 0\; \backslash \backslash \; 0\; k\; \backslash \; end\; \{bmatrix\}\}\}$	$[k\; 1\; 0\; 0\; k\; 2]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; k\_\; \{1\}\; 0\; \backslash \backslash \; 0\; k\_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\}$	$[c\; -\; ssc]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; c\; -s\; \backslash \backslash \; s\; c\; \backslash \; end\; \{bmatrix\}\}\}$. $c\; =\; cos\; \; \theta \; \{\backslash \; displaystyle\; c\; =\; \backslash \; cos\; \backslash \; theta\}$. $s\; знак\; равно\; грех\; \; \theta \; \{\backslash \; displaystyle\; s\; =\; \backslash \; sin\; \backslash \; theta\}$	$[1\; k\; 0\; 1]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 1\; k\; \backslash \backslash \; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\}$	$[cssc]\; \{\; \backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; c\; s\; \backslash \backslash \; s\; c\; \backslash \; end\; \{bmatrix\}\}\}$. $c\; =\; cosh\; \; \phi \; \{\backslash \; displaystyle\; c\; =\; \backslash \; cosh\; \backslash \; varphi\}$. $s\; =\; sinh\; \; \phi \; \{\backslash \; displaystyle\; s\; =\; \backslash \; sinh\; \backslash \; varphi\}$
Характеристика. многочлен	$(\lambda \; -\; k)\; 2\; \{\backslash \; displaystyle\; \backslash \; (\backslash \; lambda\; -k)\; ^\; \{2\}\}$	$(\lambda \; -\; k\; 1)\; (\lambda \; -\; k\; 2)\; \{\backslash \; displaystyle\; (\backslash \; lambda\; -k\_\; \{1\})\; (\backslash \; lambda\; -k\_\; \{2\})\}$	$\lambda \; 2\; -\; 2\; с\; \lambda \; +\; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{2\}\; -2c\; \backslash \; lambda\; +1\; \}$	$(\lambda \; -\; 1)\; 2\; \{\backslash \; displaystyle\; \backslash \; (\backslash \; lambda\; -1)\; ^\; \{2\}\}$	$\lambda \; 2\; -\; 2\; с\; \lambda \; +\; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{2\}\; -2c\; \backslash \; lambda\; +1\}$
собственные значения, $\lambda \; i\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{i\}\}$	$\lambda \; 1\; =\; \lambda \; 2\; знак\; равно\; К\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\; =\; \backslash \; lambda\; \_\; \{2\}\; =\; k\}$	$\lambda \; 1\; =\; k\; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\; =\; k\_\; \{1\}\}$. $\lambda \; 2\; знак\; равно\; К\; 2\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{2\}\; =\; k\_\; \{2\}\}$	$\lambda \; 1\; =\; ei\; \theta \; =\; c\; +\; si\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\; =\; e\; ^\; \{\backslash \; mathbf\; \{i\}\; \backslash \; тета\}\; знак\; равно\; с\; +\; s\; \backslash \; mathbf\; \{я\}\}$. $\lambda \; 2\; =\; е\; -\; я\; \theta \; =\; с\; -\; си\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{2\}\; =\; e\; ^\; \{-\; \backslash \; mathbf\; \{i\}\; \backslash \; theta\}\; =\; cs\; \backslash \; mathbf\; \{i\}\}$	$\lambda \; 1\; =\; \lambda \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\; =\; \backslash \; lambda\; \_\; \{2\}\; =\; 1\}$	$\lambda \; 1\; =\; e\; \phi \; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{\; 1\}\; =\; e\; ^\; \{\backslash \; varphi\}\}$. $\lambda \; 2\; =\; e\; -\; \phi \; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{2\}\; =\; e\; ^\; \{-\; \backslash \; varphi\}\}$,
Алгебраический множитель,. $\mu \; я\; знак\; равно\; \mu \; (\lambda \; я)\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{i\}\; =\; \backslash \; mu\; (\; \backslash \; lambda\; \_\; \{i\})\}$	$\mu \; 1\; =\; 2\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{1\}\; =\; 2\}$	$\mu \; 1\; знак\; равно\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{1\}\; =\; 1\}$. $\mu \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{2\}\; =\; 1\}$	$\mu \; 1\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{1\; \}\; =\; 1\}$. $\mu \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{2\}\; =\; 1\}$	$\mu \; 1\; =\; 2\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{1\}\; =\; 2\}$	$\mu \; 1\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{1\}\; =\; 1\}$. $\mu \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{2\}\; =\; 1\}$
Геометрический мульт.,. $\gamma \; я\; знак\; равно\; \gamma \; (\lambda \; я)\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{i\}\; =\; \backslash \; gamma\; (\backslash \; lambda\; \_\; \{i\})\}$	$\gamma \; 1\; =\; 2\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{1\}\; =\; 2\}$	$\gamma \; 1\; знак\; равно\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{1\}\; =\; 1\}$. $\gamma \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{2\}\; =\; 1\}$	$\gamma \; 1\; =\; 1\; \{\backslash \; displaystyl\; е\; \backslash \; гамма\; \_\; \{1\}\; =\; 1\}$. $\gamma \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{2\}\; =\; 1\}$	$\gamma \; 1\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{1\}\; =\; 1\}$	$\gamma \; 1\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{1\}\; =\; 1\}$. $\gamma \; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{2\}\; =\; 1\}$
Собственные образов	Все ненулевые образования	$u\; 1\; =\; [1\; 0]\; u\; 2\; =\; [0\; 1]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; u\_\; \{1\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; u\_\; \{2\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; end\; \{align\}\}\}$	$u\; 1\; =\; [1\; -\; i]\; u\; 2\; =\; [1\; +\; i]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; u\_\; \{1\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \}\; 1\; \backslash \backslash \; -\; \backslash \; mathbf\; \{i\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; u\_\; \{2\}\; =\; \{\backslash \; begin\; \{bmatrix\; \}\; \{\backslash \}\; 1\; \backslash \backslash \; +\; \backslash \; mathbf\; \{i\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; end\; \{align\}\}\}$	$u\; 1\; =\; [1\; 0]\; \{\backslash \; displaystyle\; u\_\; \{1\}\; =\; \{\backslash \; begin\; \{bmatr)\; ix\}\; 1\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\}\}$	$u\; 1\; =\; [1\; 1]\; u\; 2\; =\; [1\; -\; 1].\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; u\_\; \{1\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \}\; 1\; \backslash \backslash \; \{\backslash \}\; 1\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; u\_\; \{2\}\; =\; \{\backslash \; begin\; \{bmatrix\; \}\; \{\backslash \}\; 1\; \backslash \backslash \; -\; 1\; \backslash \; end\; \{bmatrix\}\}.\; \backslash \; End\; \{align\}\}\}$

Характеристическое уравнение для вращения - это квадратное уравнение с дискриминантом $D\; =\; -\; 4\; (sin\; \; \theta )\; 2\; \{\backslash \; displaystyle\; D\; =\; -4\; (\backslash \; sin\; \backslash \; theta)\; ^\; \{2\}\}$, которое является отрицательным числом, если θ не является целым кратным 180 °. Следовательно, за исключением этих случаев, два собственных значения комплексными числами, $cos\; \; \theta \; \pm \; i\; sin\; \; \theta \; \{\backslash \; displaystyle\; \backslash \; cos\; \backslash \; theta\; \backslash \; pm\; \backslash \; mathbf\; \{i\}\; \backslash \; sin\; \backslash \; theta\}$; и все собственные конструкции имеют ненастоящие элементы. В самом деле, за исключением частных частных случаев, поворот изменяет направление любого ненулевого вектора на плоскости.

Линейное преобразование, которое преобразует квадрат в прямоугольник той же площади (сжатия ), имеет обратные значения собственные значения.

Уравнение Шредингера

Волновые функции , связанные с связанными состояниями электрона в атоме водорода, можно рассматривать как собственные конструкции гамильтониана атома водорода, а также оператора углового момента . Они связаны с собственными значениями, интерпретируемыми как их энергия (возрастающие вниз: $n\; =\; 1,\; 2,\; 3,\dots \; \{\backslash \; displaystyle\; n\; =\; 1,\; \backslash ,\; 2,\; \backslash ,\; 3,\; \backslash ,\; \backslash \; ldots\}$) и угловой момент (увеличивается по: s, p, d,...). На рисунке показан квадрат абсолютного значения волновых функций. Более яркие области соответствуют более высокой плотности вероятности для позиции измерения. В центре каждого рисунка находится атомное ядро ​​, протон.

Пример уравнения собственных значений, в котором представлено преобразование $T\; \{\backslash \; displaystyle\; T\}$в терминах дифференциального оператора - это не зависящее от времени уравнение Шредингера в квантовой механике :

$H\; \psi \; E\; =\; E\; \psi \; E\; \{\backslash \; displaystyle\; H\; \backslash \; psi\; \_\; \{E\}\; =\; E\; \backslash \; psi\; \_\; \{E\}\; \backslash ,\}$

где $H\; \{\backslash \; displaystyle\; H\}$, гамильтониан, является дифференциальным оператором второго порядка и $\psi \; E\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{E\}\}$, волновая функция , является одной из его собственных функций, соответствующих собственному значению $E\; \{\backslash \; displaystyle\; E\}$, интерпретируемое как его энергия.

Однако в случае, когда вас интересуют только решения связанного состояния уравнения Шредингера, нужно искать $\psi \; E\; \{\; \backslash \; displaystyle\; \backslash \; psi\; \_\; \{E\}\}$в пространстве квадратично интегрируемых функций. Поскольку это пространство является гильбертовым пространством с четко определенным скалярным произведением , можно ввести базисный набор , в котором $\psi \; E\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{E\}\}$и $H\; \{\backslash \; displaystyle\; H\}$могут быть представлены как одномерный массив (т. е. вектор) и матрица соответственно. Это позволяет представить уравнение Шредингера в матричной форме.

В этом контексте часто используется обозначение скобками. Вектор, представляющий состояние системы, в гильбертовом пространстве квадратично интегрируемых функций представлен как $|\; \Psi \; E⟩\; \{\backslash \; displaystyle\; |\; \backslash \; Psi\; \_\; \{E\}\; \backslash \; rangle\}$. В этих обозначениях уравнение Шредингера имеет вид:

$H\; |\; \Psi \; E⟩\; =\; E\; |\; \Psi \; E⟩\; \{\backslash \; displaystyle\; H\; |\; \backslash \; Psi\; \_\; \{E\}\; \backslash \; rangle\; =\; E\; |\; \backslash \; Psi\; \_\; \{E\}\; \backslash \; rangle\}$

где $|\; \Psi \; E⟩\; \{\backslash \; displaystyle\; |\; \backslash \; Psi\; \_\; \{E\}\; \backslash \; rangle\}$- собственное состояние из $H\; \{\backslash \; displaystyle\; H\}$и $E\; \{\backslash \; displaystyle\; E\}$представляет собственное значение. $H\; \{\backslash \; displaystyle\; H\}$- наблюдаемый самосопряженный оператор, бесконечномерный аналог эрмитовых матриц. Как и в матричном случае, в приведенном выше уравнении $H\; |\; \Psi \; E⟩\; \{\backslash \; displaystyle\; H\; |\; \backslash \; Psi\; \_\; \{E\}\; \backslash \; rangle\}$понимается как вектор, полученный с помощью преобразования $H\; \{\backslash \; displaystyle\; H\}$к $|\; \Psi \; E⟩\; \{\backslash \; displaystyle\; |\; \backslash \; Psi\; \_\; \{E\}\; \backslash \; rangle\}$.

Молекулярные орбитали

В квантовой механике и, в частности, в атомной и молекулярная физика, в рамках теории Хартри – Фока, атомные и молекулярные орбитали могут быть определены с помощью собственных векторов Фока. оператор. Соответствующие собственные значения интерпретируются как потенциалы ионизации согласно теореме Купманса. В этом случае термин собственный вектор используется в несколько более общем смысле, поскольку оператор Фока явно зависит от орбиталей и их собственных значений. Таким образом, если кто-то хочет подчеркнуть этот аспект, говорят о нелинейных задачах на собственные значения. Такие уравнения обычно решаются с помощью процедуры итераций, называемой в данном случае методом самосогласованного поля. В квантовой химии часто представляют уравнение Хартри – Фока в не- ортогональном базисном наборе. Это конкретное представление является обобщенной проблемой собственных значений, называемой уравнениями Рутана.

Геология и гляциология

В геологии, особенно при изучении ледникового До собственные векторы и собственные значения используются в качестве метода, с помощью которого масса информации об ориентации и падении составляющих кластовой ткани может быть суммирована в трехмерном пространстве шестью числами. В полевых условиях геолог может собрать такие данные для сотен или тысяч обломков в образце почвы, которые можно сравнить только графически, например, на диаграмме Tri-Plot (Sneed and Folk) или в виде диаграммы. Стереосеть на сети Вульфа.

Выходные данные для тензора ориентации находятся в трех ортогональных (перпендикулярных) осях пространства. Три собственных вектора упорядочены $v\; 1,\; v\; 2,\; v\; 3\; \{\backslash \; displaystyle\; v\_\; \{1\},\; v\_\; \{2\},\; v\_\; \{3\}\}$по своим собственным значениям $E\; 1\; \ge \; E\; 2\; \ge \; E\; 3\; \{\backslash \; displaystyle\; E\_\; \{1\}\; \backslash \; geq\; E\_\; \{2\}\; \backslash \; geq\; E\_\; \{3\}\}$;$v\; 1\; \{\backslash \; displaystyle\; v\_\; \{1\}\}$, то первичная ориентация / угол наклона класса, $v\; 2\; \{\backslash \; displaystyle\; v\_\; \{2\}\}$- вторичный, а $v\; 3\; \{\backslash \; displaystyle\; v\_\; \{3\}\}$- третичный, в с точки зрения прочности. Класс Аст-ориентация определяется как направление собственного вектора на розетке компаса на 360 °. Наклон измеряется как собственное значение, модуль тензора: он оценивается от 0 ° (без наклона) до 90 ° (по вертикали). Относительные значения $E\; 1\; \{\backslash \; displaystyle\; E\_\; \{1\}\}$, $E\; 2\; \{\backslash \; displaystyle\; E\_\; \{2\}\}$и $E\; 3\; \{\backslash \; displaystyle\; E\_\; \{3\}\}$продиктованы природой ткани осадка. Если $E\; 1\; =\; E\; 2\; =\; E\; 3\; \{\backslash \; displaystyle\; E\_\; \{1\}\; =\; E\_\; \{2\}\; =\; E\_\; \{3\}\}$, ткань называется изотропной. Если $E\; 1\; =\; E\; 2>E\; 3\; \{\backslash \; displaystyle\; E\_\; \{1\}\; =\; E\_\; \{2\}>E\_\; \{3\}\}$, ткань считается плоской. Если $E\; 1>E\; 2>E\; 3\; \{\backslash \; displaystyle\; E\_\; \{1\}>E\_\; \{2\}>E\_\; \{3\}\}$, ткань считается линейной.

Анализ основных компонентов

PCA многомерное распределение Гаусса с центром в $(1,\; 3)\; \{\backslash \; displaystyle\; (1,3)\}$со стандартным 3 примерно в $(0,878,\; 0,478)\; \{\backslash \; displaystyle\; (0.878,0.478)\}$направление и 1 в ортогональном направлении. Показанные стандарты являются единичными собственными векторами ковариационной матрицы (симметричной, положительно-полуопределенной) , масштабированной квадратным корнем из соответствующего собственного значения. (Как и в одномерном случае, извлекается квадратный корень, потому что стандартное отклонение легче визуализировать, чем дисперсия.

собственное разложение из симметричная положительно полуопределенная (PSD) матрица дает ортогональный базис векторов, каждый из которых имеет неотрицательное собственное значение. Ортогональное разложение PSD Матрица используется в многомерном анализе, где выборка ковариационных матриц - это PSD. Это ортогональное разложение называется анализом главных компонентов (PCA) в статистике. PCA изучает линейные отношения PCA выполняется на ковариационной матрице или корреляционной матрице (в которой каждая переменная масштабируется, чтобы иметь ее выборочная дисперсия равна единице). стандартные компоненты соответствуют основным компонентм, собственные значения - >по базовому компоненту. Анализ главных компонентов корреляционной матрицы обеспечивает ортогональный базис для пространства наблюдаемых данных: в этом базисе самые большие собственные значения соответствуют основным компонентам, которые связаны с большей частью ковариабельности среди ряда наблюдаемых данных.

Анализ главных компонентов как средство уменьшение размера компонентов при изучении больших наборов данных, таких как, которые встречаются в биоинформатике. В Q-методологии собственные значения корреляционной матрицы определяют суждение Q-методолога практической значимости (которое отличается от статистической значимости из проверки гипотез ; см. критерий определения количества факторов ). В более общем смысле, анализ главным положением какое значение как метод факторного анализа в моделировании структурным уравнением.

Анализ вибрации

Проблемы возникают естественным образом при расчете вибрации механических конструкций со многими степенями свободы. Собственные значения - это собственные частоты (или собственные частоты ) вибрации, собственные значения - это формы этих форм колебаний. В частности, незатухающая вибрация регулируется

$mx\; ¨\; +\; kx\; =\; 0\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{x\}\}\; +\; kx\; =\; 0\}$

или

$mx\; ¨\; =\; -\; kx\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{x\}\}\; =\; -\; kx\}$

, то есть ускорение пропорционально положению (т.е. мыем, что $x\; \{\backslash \; displaystyle\; x\}$будет синусоидальным во времени).

В измерениях $n\; \{\backslash \; displaystyle\; n\}$, $m\; \{\backslash \; displaystyle\; m\}$становится матрицей масс и $к\; \{\backslash \; displaystyle\; k\}$a матрица жесткости. Допустимые решения предоставить собой линейную комбинацию решений обобщенной задачи на собственные значения

$kx\; =\; \omega \; 2\; mx\; \{\backslash \; displaystyle\; kx\; =\; \backslash \; omega\; ^\; \{2\}\; mx\}$

где $\omega \; 2\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{2\}\}$- собственное значение, а $\omega \; \{\backslash \; displaystyle\; \backslash \; omega\}$- (мнимая) угловая частота. Основные режимы колебаний отличаются от основных режимов податливости, которые являются собственными явлениями только $k\; \{\backslash \; displaystyle\; k\}$. Кроме того, затухающая вибрация, управляемая

$mx\; ¨\; +\; cx\; \dot{}\; +\; kx\; =\; 0\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{x\}\}\; +\; c\; \{\backslash \; dot\; \{x\}\}\; +\; kx\; =\; 0\}$

приводит к так называемой квадратичной задаче на собственные значения,

$(\omega \; 2\; m\; +\; \omega \; c\; +\; k)\; x\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\backslash \; omega\; ^\; \{2\}\; m\; +\; \backslash \; omega\; c\; +\; k\; \backslash \; right)\; x\; =\; 0.\}$

Это можно свести к обобщенной задаче собственных значений с алгебраических манипуляций за счет решения более крупной системы.

Свойства ортогональности собственных векторов позволяют разделить дифференциальные уравнения, так что система может быть представлена ​​как линейное суммирование собственных векторов. Проблема собственных элементов сложных конструкций часто решается с использованием анализа конечных элементов, но точно обобщает решение для задач вибрации со скалярными значениями.

Собственные лица

Собственные лица как примеры собственных векторов

В обработка изображений обработанные изображения лиц можно рассматривать как элементы, являющиеся яркости каждого пикселя. Размерность этого пространства - это количество пикселей. Собственные стандартные ковариационные матрицы , содержат с большим набором нормализованных изображений лиц, называются eigenfaces ; это пример анализа главных компонентов. Они очень полезны для выражения любого изображения лица в виде линейной комбинации некоторых из них. В ветви распознавания лиц раздела биометрии собственные лица используют средство применения сжатия данных к лицам для идентификации целей. Также были проведены исследования, связанные с системами собственного зрения, определяющими жесты рук.

Подобно этой концепции, собственные голоса представляют общее направление изменчивости такого произношения данного высказывания, как слово на языке. На основе линейной комбинации таких голосов можно построить новое голосовое произношение слова. Эти концепции полезными в системе автоматического распознавания речи для адаптации говорящего.

Тензор момента инерции

В механике конструирование собственных тензора момента инерции определяет главные оси твердого тела . тензор момента инерции является ключевой величиной, необходимой для вращения твердого тела вокруг его центра масс.

тензор напряжений

механике деформируемого твердого тела тензор напряжений является симметричным и поэтому может быть разложен на диагональный тензор с собственными значениями на диагонали и собственными векторми в качестве основы. Он указывает на диагонален, в этой ориентации тензор напряжений не имеет компонентов сдвига ; компоненты, которые он имеет, вызывающие компоненты.

Графы

В теории спектральных графов собственное значение графа определяет как собственное значение матрицы матрицы графа $A\; \{\; \backslash \; displaystyle\; A\}$, или (в возрастающей степени) матрицы Лапласа графа из-за его дискретного оператора Лапласа, который либо $D\; -\; A\; \{\backslash \; displaystyle\; DA\}$(иногда называемый комбинаторным лапласианом) или $I\; -\; D\; -\; 1/2\; AD\; -\; 1/2\; \{\backslash \; displaystyle\; ID\; ^\; \{-\; 1/2\}\; AD.\; ^\; \{-\; 1/2\}\}$(иногда называемый нормализованным лапласианом), где $D\; \{\backslash \; displaystyle\; D\}$- диагональная матрица с $D\; ii\; \{\backslash \; displaystyle\; D\_\; \{ii\}\}$равно степени вершины $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$, а в $D\; -\; 1/2\; \{\backslash \; displaystyle\; D\; ^\; \{-\; 1\; /\; 2\}\}$, $i\; \{\backslash \; displaystyle\; i\}$-й диагональный элемент равен $1\; /\; deg\; \; (vi)\; \{\backslash \; displaystyle\; 1\; /\; \{\backslash \; sqrt\; \{\; \backslash \; deg\; (v\_\; \{i\})\}\}\}$. $k\; \{\backslash \; displaystyle\; k\}$-й главный собственный вектор графа определяет как собственный вектор, соответствующий $k\; \{\backslash \; displaystyle\; k\}$-ому наибольшему значению или $k\; \{\backslash \; displaystyle\; k\}$-ое наименьшее собственное значение лапласиана. Первый главный вектор графа также называется просто собственным собственным вектором.

Главный собственный вектор используется для измерения центральные его вершин. Примером может быть алгоритм Google PageRank. Главный собственный вектор модифицированной матрицы компонентности графа страницы Всемирной паутины определяет ранги как ее компоненты. Этот вектор соответствует стационарному распределению цепи Маркова, представленной нормализованной по строкам матрицей линейности; однако сначала необходимо изменить матрицу последовательности. Второй наименьший собственный вектор можно использовать для разделения графа на кластеры с помощью спектральной кластеризации. Также доступны другие методы кластеризации.

Базовый номер репродукции

Базовый номер репродукции ($R\; 0\; \{\backslash \; displaystyle\; R\_\; \{0\}\}$) является фундаментальным числом в исследовании того, насколько заразны распространения болезней. Если один инфекционный человек попадает в группу полностью восприимчивых людей, то $R\; 0\; \{\backslash \; displaystyle\; R\_\; \{0\}\}$- это среднее количество людей, которое заразит один типичный инфекционный человек. Время генерации инфекции - это время, $t\; G\; \{\backslash \; displaystyle\; t\_\; \{G\}\}$, от инфицированного человека до заражения следующего. В гетерогенной популяции матрица следующего поколения определяет, сколько человек в популяции происходит по прошествии времени $t\; G\; \{\backslash \; displaystyle\; t\_\; \{G\}\}$. $R\; 0\; \{\backslash \; displaystyle\; R\_\; \{0\}\}$тогда имеет наибольшее значение длины матрицы следующего поколения.

См. Также

• Теория антисобственных значений
• Собственный оператор
• Собственная плоскость
• Алгоритм собственных значений
• Введение в собственные
• нормальная форма Джордана
• Список программного численного анализа
• Нелинейная задача собственных значений
• Нормальное собственное значение
• Квадратичная конструкция на собственные значения
• Сингулярное значение
• Спектр матрицы

Примечания

Цитаты

Источники

Дополнительная литература

Внешние ссылки

Викибук Линейная алгебра страница по теме: Собственные значения и собственные значения

• Что такое собственные значения? - нетехническое введение из статьи "Спросите экспертов" на сайте PhysLink.com
• Численные значения значений и собственных векторов - Обучающая и интерактивная программа от Revoledu.
• Введение в собственные конструкции и собственные значения - лекция из Академии Хана
• Собственные конструкции и собственные значения | Суть линейной алгебры, глава 10 - Наглядное объяснение с помощью 3Blue1Brown
• Калькулятор собственных векторов матрицы от Symbolab (Нажмите на нижнюю правую кнопку сетки 2x12, чтобы выбрать размер матрицы. Выберите $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$размер (для квадратной матрицы), затем введите числовые значения и нажмите кнопку «Перейти».

Теория

• , Энциклопедия математики, EMS Press, 2001 [1994]
• , Энциклопедия математики, EMS Press, 2001 [1994]
• «Собственное значение (матрицы)». PlanetMath.
• Eigenvector - Wolfram MathWorld
• Рабочий апплет исследования собственных векторов
• То же исследование собственных векторов, что и выше, во флэш-демонстрации со звуком
• Вычисление собственных значений
• Числовое решение задач на собственных значениях Под редакцией Чжаоджун Бая, Джеймса Деммеля, Джека Донгарра, Акселя Рухе и Хенка ван дер Ворста
• Собственные значения и собственные значения на форумах Спросите Dr. Math: [1], [2]

Демонстрационные апплеты

• Java-апплет о настрох в реальной плоскости
• Функциональность языка Wolfram Language для собственных значений, собственных векторов и собственных систем