Однородное отношение

редактировать

В математике, А однородное отношение (также называемый endorelation) над множеством X представляет собой бинарное отношение над X и сам, т.е. подмножество декартова произведения X × X. Это также просто называется (бинарное) отношение над X. Примером гомогенного отношения является отношение родства, где отношение распространяется на людей.

Однородное отношение R над множеством X может быть отождествлено с ориентированным простым графом, допускающим петли, или, если оно симметрично, с неориентированным простым графом, допускающим петли, где X - множество вершин, а R - множество ребер (есть ребро из вершины x в вершину y тогда и только тогда, когда xRy). Это называется отношением смежности графа.

Множество всех однородных отношений над множеством X - это множество 2 ^X ^× ^X, которое является булевой алгеброй, дополненной инволюцией отображения отношения в обратное отношение. Рассматривая композицию отношений как бинарную операцию над, она образует полугруппу с инволюцией. ${\ Displaystyle {\ mathcal {B}} (X)}$ ${\ Displaystyle {\ mathcal {B}} (X)}$ ${\ Displaystyle {\ mathcal {B}} (X)}$ ${\ Displaystyle {\ mathcal {B}} (X)}$

СОДЕРЖАНИЕ

1 Особые однородные отношения
- 1.1 Пример
2 свойства
3 Операции
4 Перечисление
5 примеров
6 Обобщения
7 ссылки

Особые однородные отношения

Некоторые важные частные однородные отношения над множеством X (с произвольными элементами x 1, x 2):

Пустое отношение: Е = ∅ ⊆ Х × Х, т.е. х 1 Пример 2 не имеет никогда;
Универсальное отношение: U = X × X, т. Е. X 1 Ux 2 всегда выполняется;
Отношение идентичности: I = {( x, x) | x ∈ X }, т.е. x 1 Ix 2 выполняется тогда и только тогда, когда x 1 = x 2.

Пример

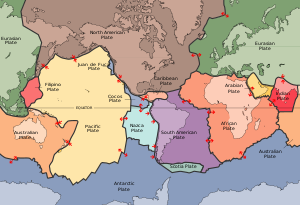
Пятнадцать крупных тектонических плит земной коры однородно соприкасаются друг с другом. Отношение может быть выражено в виде логической матрицы, где 1 указывает на контакт, а 0 - на отсутствие контакта. Этот пример выражает симметричное отношение.

Характеристики

См. Также: Категория: Бинарные отношения

Некоторые важные свойства, которыми может обладать однородное отношение R над множеством X:

Рефлексивный: для всех x ∈ X, xRx. Например, ≥ - рефлексивное отношение, аgt; - нет.
Нерефлексивный (или строгий): для всех x ∈ X, а не xRx. Например,gt; - иррефлексивное отношение, а ≥ - нет.
Coreflexive: для всех x, y ∈ X, если xRy, то x = y. Например, отношение целых чисел, в котором каждое нечетное число связано с самим собой, является коререфлексивным отношением. Отношение равенства - единственный пример как рефлексивного, так и корефлексивного отношения, а любое корефлексивное отношение является подмножеством отношения идентичности.
Левый квазирефлексивный: для всех x, y ∈ X, если xRy, то xRx.
Правый квазирефлексивный: для всех x, y ∈ X, если xRy, то yRy.
Квазирефлексивный: для всех x, y ∈ X, если xRy, то xRx и yRy. Отношение квазирефлексивно тогда и только тогда, когда оно квазирефлексивно как слева, так и справа.

Предыдущие 6 альтернатив далеко не исчерпывающие; например, красное бинарное отношение y = x ^{2 не} является ни иррефлексивным, ни корефлексивным, ни рефлексивным, поскольку оно содержит пару (0, 0) и (2, 4), но не (2, 2), соответственно. Последние два факта также исключают (любую) квазирефлексивность.

Симметричный: для всех x, y ∈ X, если xRy, то yRx. Например, «является кровным родственником» является симметричным отношением, потому что x является кровным родственником y тогда и только тогда, когда y является кровным родственником x.
Антисимметричный: для всех x, y ∈ X, если xRy и yRx, то x = y. Например, ≥ - антисимметричное отношение; так естьgt;, но бессмысленно (условие в определении всегда ложно).
Асимметричный: для всех x, y ∈ X, если xRy, то не yRx. Отношение асимметрично тогда и только тогда, когда оно одновременно антисимметрично и иррефлексивно. Например,gt; - это асимметричное отношение, а ≥ - нет.

Опять же, предыдущие 3 альтернативы далеко не исчерпывающие; в качестве примера для натуральных чисел отношение xRy, определяемое x gt; 2, не является ни симметричным, ни антисимметричным, не говоря уже об асимметричном.

Переходный: для всех x, y, z ∈ X, если xRy и yRz, то xRz. Транзитивное отношение иррефлексивно тогда и только тогда, когда оно асимметрично. Например, «является предком» является транзитивным отношением, а «является родителем» - нет.
Антитранзитивный: для всех x, y, z ∈ X, если xRy и yRz, то никогда не xRz.
Ко-транзитивный: если дополнение к R транзитивно. То есть для всех x, y, z ∈ X, если xRz, то xRy или yRz. Это используется в псевдопорядках в конструктивной математике.
Квазитранзитивный: для всех x, y, z ∈ X, если xRy и yRz, но не yRx и zRy, то xRz, но не zRx.
Транзитивность несравнимости: для всех х, у, г ∈ X, если х и у не сравнимы по отношению к R, и если то же самое можно сказать и о у и г, то х и г, также несравнима по отношению к R. Это используется в слабом порядке.

Опять же, предыдущие 5 альтернатив не являются исчерпывающими. Например, отношение xRy if ( y = 0 или y = x +1) не удовлетворяет ни одному из этих свойств. С другой стороны, пустое отношение тривиально им всем удовлетворяет.

Плотный: для всех x, y ∈ X таких, что xRy, существует некоторый z ∈ X такой, что xRz и zRy. Это используется в плотных заказах.
Связаны: для всех x, y ∈ X, если x ≠ y, то xRy или yRx. Это свойство иногда называют «общим», что отличается от определений «всего слева / справа», приведенных ниже.
Сильно связан: для всех x, y ∈ X, xRy или yRx. Это свойство также иногда называют «общим», что отличается от определений «всего слева / справа», приведенных ниже.
Трихотомический: для всех x, y ∈ X выполняется ровно одно из xRy, yRx или x = y. Например,gt; - это трихотомическое отношение, в то время как отношение «делится» на натуральные числа - нет.
Право евклидово (или просто евклидово): для всех x, y, z ∈ X, если xRy и xRz, то yRz. Например, = является евклидовым соотношением, потому что если x = y и x = z, то y = z.
Левый евклидов: для всех x, y, z ∈ X, если yRx и zRx, то yRz.
Обоснованный: каждое непустое подмножество S из X содержит минимальный элемент по отношению к R. Обоснованность подразумевает условие убывающей цепи (то есть, бесконечная цепочка... x n R... Rx 3 Rx 2 Rx 1 существовать не может). Если принять аксиому зависимого выбора, оба условия эквивалентны.

Более того, все свойства бинарных отношений в целом также могут применяться к однородным отношениям:

Как набор: для всех х ∈ X, то класс всех у таких, что угх представляет собой набор. (Это имеет смысл, только если разрешены отношения над соответствующими классами.)
Лево-уникальный: для всех x, z ∈ X и всех y ∈ Y, если xRy и zRy, то x = z.
Право-уникальный: для всех x ∈ X и всех y, z ∈ Y, если xRy и xRz, то y = z.
Последовательный (также называемый полным слева): для всех x ∈ X существует y ∈ Y такой, что xRy. Это свойство, хотя некоторые авторы также называют его общим, отличается от определения связного (также называемого некоторыми авторами общим).
Сюръективный (также называемый справа-тотальным): для всех y ∈ Y существует x ∈ X такой, что xRy.

Предварительный заказ - это рефлексивное и транзитивное отношение. Общая предпорядок, называемая также линейный предпорядком или слабого для того, является отношением, которое является рефлексивным, транзитивным, и подключено.

Частичный порядок, называемый также порядок, это отношение, которое является рефлексивным, антисимметричным и транзитивным. Строгий частичный порядок, называемый также строгий порядок, это отношение, которое иррефлексивно, антисимметричным и транзитивным. Общий порядок, называемый также линейный порядок, простой порядок, или цепь, является отношение, которое является рефлексивным, антисимметричным, транзитивным и подключен. Строгий общий порядок, называемый также строгий линейный порядок, строгий порядок простой, или строгая цепь, является отношением, что иррефлексивно, антисимметричным, транзитивным и подключен.

Частичное отношение эквивалентности является отношением, которое является симметричным и транзитивным. Отношение эквивалентности есть отношение, которое рефлексивно, симметрично и транзитивно. Это также отношение, которое является симметричным, транзитивным и последовательным, поскольку эти свойства подразумевают рефлексивность.

Последствия и конфликты между свойствами однородных бинарных отношений
Последствия (синий) и конфликты (красный) между свойствами (желтый) однородных бинарных отношений. Например, каждый асимметричное соотношение иррефлексивное ( « асим ⇒ Irrefl »), а не отношение на непустое множестве не может быть одновременно иррефлексивным и рефлексивным ( « Irrefl # Refl »). Отсутствие красных краев приводит к диаграмме Хассе.

Операции

Если R является однородным отношением над множеством X, то каждое из следующих отношений является однородным отношением над X:

Рефлексивное закрытие, R ⁼: Определяется как R ⁼ = {( x, x) | х ∈ Х } ∪ R или наименьшее рефлексивное отношение над X, содержащей R. Это может быть доказано, чтобы быть равным пересечение всех рефлекторных отношений, содержащих R.
Рефлексивное сокращение, R ^≠: Определяется как R ^≠ = R \ {( x, x) | х ∈ Х } или по величине иррефлексивного отношения над X, содержащимся в R.
Переходное замыкание, R ⁺: Определяется как наименьшее транзитивное отношение над X, содержащей R. Это можно видеть, равно пересечению всех транзитивных отношений, содержащих R.
Рефлексивное переходное замыкание, R *: Определяется как R * = ( R ⁺) ⁼ наименьшее предпорядок, содержащий R.
Рефлексивное транзитивное симметричное замыкание, R ^≡: Определяется как наименьшее отношение эквивалентности над X, содержащей R.

Все операции, определенные в бинарных отношениях § Операции с бинарными отношениями также применимы к однородным отношениям.

Однородные отношения по собственности
	Рефлексивность	Симметрия	Транзитивность	Связность	Условное обозначение	Пример
Направленный граф					→
Ненаправленный граф		Симметричный
Зависимость	Рефлексивный	Симметричный
Турнир	Нерефлексивный	Антисимметричный				Порядок иерархии
Предзаказ	Рефлексивный		Переходный		≤	Предпочтение
Всего предзаказ	Рефлексивный		Переходный	Связаны	≤
Частичный заказ	Рефлексивный	Антисимметричный	Переходный		≤	Подмножество
Строгий частичный заказ	Нерефлексивный	Антисимметричный	Переходный		lt;	Строгое подмножество
Общий заказ	Рефлексивный	Антисимметричный	Переходный	Связаны	≤	Алфавитный порядок
Строгий общий порядок	Нерефлексивный	Антисимметричный	Переходный	Связаны	lt;	Строгий алфавитный порядок
Отношение частичной эквивалентности		Симметричный	Переходный
Отношение эквивалентности	Рефлексивный	Симметричный	Переходный		∼, ≡	Равенство

Перечисление

Количество различных однородных отношений над n -элементным множеством равно 2 ^{n ²} (последовательность A002416 в OEIS ):

Количество n -элементных бинарных отношений разных типов
Элементы	Любой	Переходный	Рефлексивный	Предзаказ	Частичный заказ	Всего предзаказ	Общий заказ	Отношение эквивалентности
0	1	1	1	1	1	1	1	1
1	2	2	1	1	1	1	1	1
2	16	13	4	4	3	3	2	2
3	512	171	64	29	19	13	6	5
4	65 536	3,994	4096	355	219	75	24	15
п	2 ^{п ²}		2 ^{п ² - п}			${\ textstyle \ sum _ {k = 0} ^ {n} k!}$ ${\ textstyle \ sum _ {k = 0} ^ {n} k!}$ S ( п, к)	п !	${\ textstyle \ сумма _ {к = 0} ^ {п}}$ ${\ textstyle \ сумма _ {к = 0} ^ {п}}$ S ( п, к)
OEIS	A002416	A006905	A053763	A000798	A001035	A000670	A000142	A000110

Примечания:

Количество иррефлексивных отношений такое же, как и количество рефлексивных отношений.
Количество строгих частичных порядков (иррефлексивных транзитивных отношений) такое же, как и у частичных порядков.
Количество строгих слабых заказов такое же, как и общее количество предварительных заказов.
Общие заказы - это частичные заказы, которые также являются общими предварительными заказами. Таким образом, количество предварительных заказов, которые не являются ни частичным, ни полным предварительным заказом, равно количеству предварительных заказов минус количество частичных заказов, минус общее количество предварительных заказов, плюс общее количество заказов: 0, 0, 0, 3 и 85 соответственно.
Количество отношений эквивалентности - это количество разделов, которое является числом Белла.

Однородные отношения можно сгруппировать в пары (отношение, дополнение ), за исключением того, что при n = 0 отношение является своим собственным дополнением. Несимметричные могут быть сгруппированы в четверки (отношение, дополнение, обратное, обратное дополнение).

Примеры

Порядковые отношения, в том числе строгие приказы :
- Больше чем
- Больше или равно
- Меньше, чем
- Меньше или равно
- Делит (равномерно)
- подмножеству из
Отношения эквивалентности :
- Равенство
- Параллельно с (для аффинных пространств )
- Равномерность или " взаимно однозначно "
- Изоморфный
Отношение толерантности, рефлексивное и симметричное отношение:
- Отношение зависимости, отношение конечной терпимости
- Отношение независимости, дополнение некоторого отношения зависимости
Родственные отношения

Обобщения

Бинарное отношение вообще не должны быть однородным, оно определяется как подмножество R ⊆ X × Y для произвольных множеств X и Y.
Финитарное отношение представляет собой подмножество R ⊆ X 1 ×... × Х п для некоторого натурального числа п и произвольных множеств X 1,..., Х п, это также называется п -ичного отношения.

использованная литература