Симметричное отношение

Транзитивные   бинарные отношения
Симметричный Антисимметричный Связаны Обоснованный Присоединяется Встречается Рефлексивный Нерефлексивный Асимметричный Также известный как: Итого, Semiconnex Антирефлексивный Отношение эквивалентности ✓ ✗ ✗ ✗ ✗ ✗ ✓ ✗ ✗ Предзаказ (Квазипорядок) ✗ ✗ ✗ ✗ ✗ ✗ ✓ ✗ ✗ Частичный заказ ✗ ✓ ✗ ✗ ✗ ✗ ✓ ✗ ✗ Всего предзаказ ✗ ✗ ✓ ✗ ✗ ✗ ✓ ✗ ✗ Общий заказ ✗ ✓ ✓ ✗ ✗ ✗ ✓ ✗ ✗ Предварительный заказ ✗ ✗ ✓ ✓ ✗ ✗ ✓ ✗ ✗ Хорошо-квазиупорядоченный ✗ ✗ ✗ ✓ ✗ ✗ ✓ ✗ ✗ Хороший порядок ✗ ✓ ✓ ✓ ✗ ✗ ✓ ✗ ✗ Решетка ✗ ✓ ✗ ✗ ✓ ✓ ✓ ✗ ✗ Соединение-полурешетка ✗ ✓ ✗ ✗ ✓ ✗ ✓ ✗ ✗ Встреча-полурешетка ✗ ✓ ✗ ✗ ✗ ✓ ✓ ✗ ✗ Строгий частичный заказ ✗ ✗ ✗ ✗ ✗ ✗ ✗ ✓ ✓ Строгий слабый порядок ✗ ✗ ✗ ✗ ✗ ✗ ✗ ✓ ✓ Строгий общий порядок ✗ ✗ ✓ ✗ ✗ ✗ ✗ ✓ ✓ Симметричный Антисимметричный Связаны Обоснованный Присоединяется Встречается Рефлексивный Нерефлексивный Асимметричный Определения: ${\ displaystyle \ scriptstyle {{\ text {Для всех}} \, a, b \, {\ text {and}} \, S \ neq \ varnothing:}}$ ${\ displaystyle \ scriptstyle {aRb \ Rightarrow bRa}}$ ${\ displaystyle \ scriptstyle {aRb \, {\ text {and}} \, bRa \ Rightarrow a = b}}$ ${\ displaystyle \ scriptstyle {a \ neq b \ Rightarrow aRb \, {\ text {или}} \, bRa}}$ ${\ displaystyle \ scriptstyle {\ min S \, {\ text {exists}}}}$ ${\ displaystyle \ scriptstyle {a \ vee b \, {\ text {exists}}}}$ ${\ Displaystyle \ scriptstyle {а \ клин б \, {\ текст {существует}}}}$ ${\ displaystyle \ scriptstyle {aRa}}$ ${\ displaystyle \ scriptstyle {{\ text {not}} \, aRa}}$ ${\ displaystyle \ scriptstyle {aRb \ Rightarrow {\ text {not}} \, bRa}}$
Все определения неявно требуют, чтобы однородное отношение было транзитивным : « ✓ » указывает, что свойство столбца требуется в определении строки. Например, определение отношения эквивалентности требует, чтобы оно было симметричным. Упомянутые здесь дополнительные свойства, что однородное отношение может удовлетворять. ${\ displaystyle R}$ ${\ displaystyle \ scriptstyle {{\ text {Для всех}} \, a, b, c, {\ text {if}} aRb {\ text {and}} bRc {\ text {then}} aRc}.}$

Симметричное отношение представляет собой тип бинарного отношения. Примером может служить отношение «равно», потому что если a = b истинно, то b = a также истинно. Формально бинарное отношение R над множеством X является симметричным, если:

${\ displaystyle \ forall a, b \ in X (aRb \ Leftrightarrow bRa),}$

где обозначение означает, что. ${\ displaystyle aRb}$${\ displaystyle (a, b) \ in R}$

Если Р ^Т представляет собой обратное из R, то R является симметричным тогда и только тогда, когда R = R ^T.

Симметрия, наряду с рефлексивностью и транзитивностью, являются тремя определяющими свойствами отношения эквивалентности.

СОДЕРЖАНИЕ

• 1 Примеры
  • 1.1 По математике
  • 1.2 Вне математики
• 2 Связь с асимметричными и антисимметричными отношениями
• 3 свойства
• 4 ссылки
• 5 См. Также

Примеры

По математике

• "равно" ( равенство ) (тогда как "меньше" не является симметричным)
• " сопоставимо с" для элементов частично упорядоченного множества
• "... и... нечетные":

Вне математики

• «женат на» (в большинстве правовых систем)
• "является полностью биологическим братом"
• " омофон "
• "сотрудник"
• "товарищ по команде"

Связь с асимметричными и антисимметричными отношениями

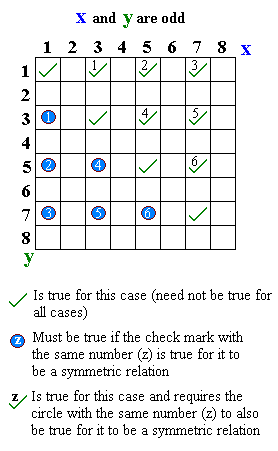
По определению непустое отношение не может быть одновременно симметричным и асимметричным (где, если a связано с b, то b не может быть связано с a (таким же образом)). Однако отношение не может быть ни симметричным, ни асимметричным, как в случае «меньше или равно» и «жертва»).

Симметричные и антисимметричные (где единственный способ могут быть связаны с б и б быть связано с, если = б) на самом деле являются независимыми друг от друга, как показывают эти примеры.

Характеристики

• Симметричное и транзитивное отношение всегда квазирефлексивно.

• Симметричное, транзитивное и рефлексивное отношение называется отношением эквивалентности.

• Один из способов концептуализировать симметричное отношение в теории графов состоит в том, что симметричное отношение - это ребро, причем две вершины ребра являются двумя объектами, связанными таким образом. Таким образом, симметричные отношения и неориентированные графы являются комбинаторно эквивалентными объектами.

использованная литература

Смотрите также

• Коммутативное свойство  - свойство, позволяющее изменять порядок операндов операции.
• Симметрия в математике  - Симметрия в математике
• Симметрия  - Математическая инвариантность относительно преобразований