Связанные многочлены Лежандра

В математике связанные многочлены Лежандра являются каноническими решениями общее уравнение Лежандра

$(1\; -\; x\; 2)\; d\; 2\; dx\; 2\; P\; \ell \; m\; (x)\; -\; 2\; xddx\; P\; \ell \; m\; (x)\; +\; [\ell \; (\ell \; +\; 1)\; -\; m\; 2\; 1\; -\; x\; 2]\; P\; \ell \; м\; (Икс)\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; (1-х\; ^\; \{2\})\; \{\backslash \; гидроразрыва\; \{d\; ^\; \{2\}\}\; \{dx\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; -\; 2x\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; +\; \backslash \; left\; [\backslash \; ell\; (\backslash \; ell\; +1)\; -\; \{\backslash \; frac\; \{m\; ^\; \{2\}\}\; \{1-x\; ^\; \{2\}\}\}\; \backslash \; right]\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; 0\}$,

или эквивалентно

$ddx\; [(1\; -\; x\; 2)\; ddx\; P\; \ell \; m\; (x)]\; +\; [\; \ell \; (\ell \; +\; 1)\; -\; м\; 2\; 1\; -\; Икс\; 2]\; п\; \ell \; м\; (x)\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \backslash \; left\; [(1-x\; ^\; \{2\})\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; \backslash \; right]\; +\; \backslash \; left\; [\backslash \; ell\; (\backslash \; ell\; +1)\; -\; \{\backslash \; frac\; \{m\; ^\; \{2\}\}\; \{1-x\; ^\; \{2\}\}\}\; \backslash \; right]\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; 0\}$,

где индексы ℓ и m (которые являются целыми числами) называются степенью и порядком связанного многочлена Лежандра. соответственно. Это уравнение имеет ненулевые решения, неособые на [−1, 1], только если ℓ и m - целые числа с 0 ≤ m ≤ ℓ или с тривиально эквивалентными отрицательными значениями. Когда вдобавок m четно, функция является полиномом . Когда m равно нулю и ℓ целое число, эти функции идентичны полиномам Лежандра. В общем, когда ℓ и m являются целыми числами, регулярные решения иногда называют «ассоциированными полиномами Лежандра», даже если они не являются полиномами, когда m нечетно. Полностью общий класс функций с произвольными действительными или комплексными значениями ℓ и m - это функции Лежандра. В этом случае параметры обычно обозначаются греческими буквами.

Обыкновенное дифференциальное уравнение Лежандра часто встречается в физике и других областях техники. В частности, это происходит при решении уравнения Лапласа (и связанных дифференциальных уравнений в частных производных ) в сферических координатах. Связанные полиномы Лежандра играют жизненно важную роль в определении сферических гармоник.

• 1 Определение неотрицательных целочисленных параметров ℓ и m
  • 1.1 Альтернативные обозначения
  • 1.2 Закрытая форма
• 2 Ортогональность
• 3 Отрицательное m и / или отрицательное ℓ
• 4 Четность
• 5 Первые несколько связанных функций Лежандра
• 6 Формула повторения
• 7 Формула Гона
• 8 Обобщение с помощью гипергеометрических функций
• 9 Повторная параметризация в терминах углов
• 10 Приложения в физике: сферические гармоники
• 11 Обобщения
• 12 См. Также
• 13 Примечания и ссылки
• 14 Внешние ссылки

Эти функции обозначаются $P\; \ell \; m\; (x)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\}$, где верхний индекс указывает порядка, а не степени P. Их наиболее прямое определение дано в терминах производных обычных многочленов Лежандра (m ≥ 0)

$P\; \ell \; m\; (x)\; =\; (-\; 1)\; m\; (1\; -\; х\; 2)\; м\; /\; 2\; dmdxm\; (п\; \ell \; (х))\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; (-\; 1)\; ^\; \{m\}\; (1-x\; ^\; \{2\})\; ^\; \{m\; /\; 2\}\; \{\backslash \; frac\; \{d\; ^\; \{m\}\}\; \{dx\; ^\; \{m\}\}\}\; \backslash \; left\; (P\; \_\; \{\backslash \; ell\}\; (x)\; \backslash \; right)\}$,

Фактор (-1) в этой формуле известен как Фаза Кондона – Шортли. Некоторые авторы опускают его. Функции, описываемые этим уравнением, удовлетворяют общему дифференциальному уравнению Лежандра с указанными значениями параметров ℓ, и m следует путем дифференцирования m раз уравнения Лежандра для P ℓ:

$(1\; -\; x\; 2)\; d\; 2\; dx\; 2\; P\; \ell \; (x)\; -\; 2\; xddx\; п\; \ell \; (x)\; +\; \ell \; (\ell \; +\; 1)\; P\; \ell \; (x)\; =\; 0.\; \{\backslash \; displaystyle\; (1-x\; ^\; \{2\})\; \{\backslash \; frac\; \{d\; ^\; \{2\}\}\; \{dx\; ^\; \{2\; \}\}\}\; P\; \_\; \{\backslash \; ell\}\; (x)\; -2x\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; P\; \_\; \{\backslash \; ell\}\; (x)\; +\; \backslash \; ell\; (\backslash \; ell\; +1)\; P\; \_\; \{\backslash \; ell\}\; (x)\; =\; 0.\}$

Более того, поскольку по формуле Родригеса,

$P\; \ell \; (x)\; =\; 1\; 2\; \ell \; \ell !\; d\; \ell \; dx\; \ell \; [(x\; 2\; -\; 1)\; \ell ],\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; ^\; \{\backslash \; ell\}\; \backslash ,\; \backslash \; ell!\}\}\; \backslash \; \{\backslash \; frac\; \{d\; ^\; \{\backslash \; ell\}\}\; \{dx\; ^\; \{\backslash \; ell\}\}\}\; \backslash \; left\; [(x\; ^\; \{2\}\; -1)\; ^\; \{\backslash \; ell\}\; \backslash \; right],\}$

P. ℓможет быть выражено в виде

$P\; \ell \; m\; (x)\; =\; (-\; 1)\; m\; 2\; \ell \; \ell !\; (1\; -\; x\; 2)\; m\; /\; 2\; d\; \ell \; +\; m\; d\; x\; \ell \; +\; m\; (x\; 2\; -\; 1)\; \ell .\; \{\backslash \; Displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; \{\backslash \; frac\; \{(-1)\; ^\; \{m\}\}\; \{2\; ^\; \{\backslash \; ell\}\; \backslash \; ell!\}\}\; (1-x\; ^\; \{2\})\; ^\; \{m\; /\; 2\}\; \backslash \; \{\backslash \; frac\; \{d\; ^\; \{\backslash \; ell\; +\; m\}\}\; \{dx\; ^\; \{\backslash \; ell\; +\; m\}\}\}\; (x\; ^\; \{2\}\; -1)\; ^\; \{\backslash \; ell\}.\}$

Это уравнение позволяет расширить диапазон m до: −ℓ ≤ m ≤ ℓ. Определения P ℓ, полученные из этого выражения путем замены ± m, являются пропорциональными. Действительно, приравняем коэффициенты при равных степенях в левой и правой частях

$d\; \ell \; -\; mdx\; \ell \; -\; m\; (x\; 2\; -\; 1)\; \ell \; =\; clm\; (1\; -\; x\; 2)\; md\; \ell \; +\; mdx\; \ell \; +\; m\; (x\; 2-1)\; \ell ,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{\backslash \; ell\; -m\}\}\; \{dx\; ^\; \{\backslash \; ell\; -m\}\}\}\; (x\; ^\; \{2\}\; -1)\; ^\; \{\backslash \; ell\}\; =\; c\_\; \{\; lm\}\; (1-x\; ^\; \{2\})\; ^\; \{m\}\; \{\backslash \; frac\; \{d\; ^\; \{\backslash \; ell\; +\; m\}\}\; \{dx\; ^\; \{\backslash \; ell\; +\; m\}\}\}\; (x\; ^\; \{2\}\; -1)\; ^\; \{\; \backslash \; ell\},\}$

, тогда коэффициент пропорциональности

$clm\; =\; (-\; 1)\; m\; (\ell \; -\; m)!\; (\ell \; +\; м)!,\; \{\backslash \; displaystyle\; c\_\; \{lm\}\; =\; (-\; 1)\; ^\; \{m\}\; \{\backslash \; frac\; \{(\backslash \; ell\; -m)!\}\; \{(\backslash \; ell\; +\; m)!\}\},\}$

так что

$P\; \ell \; -\; м\; (х)\; знак\; равно\; (-\; 1)\; м\; (\ell \; -\; м)!\; (\ell \; +\; м)!\; P\; \ell \; m\; (x).\; \{\backslash \; Displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{-\; m\}\; (x)\; =\; (-\; 1)\; ^\; \{m\}\; \{\backslash \; frac\; \{(\backslash \; ell\; -m)!\}\; \{(\backslash \; ell\; +\; m)!\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x).\}$

Альтернативные обозначения

В литературе также используются следующие альтернативные обозначения:

$P\; \ell \; m\; (x)\; =\; (-\; 1)\; m\; P\; \ell \; m\; (x)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\; m\}\; (x)\; =\; (-\; 1)\; ^\; \{m\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\}$

Закрытая форма

Связанные Многочлен Лежандра можно также записать как:

$P\; lm\; (x)\; =\; (-\; 1)\; m\; \cdot \; 2\; l\; \cdot \; (1\; -\; x\; 2)\; m\; /\; 2\; \cdot \; \sum \; k\; =\; mlk!\; (к\; -\; м)!\; \cdot \; xk\; -\; м\; \cdot \; (lk)\; (l\; +\; k\; -\; 1\; 2\; l)\; \{\backslash \; displaystyle\; P\_\; \{l\}\; ^\; \{m\}\; (x)\; =\; (-\; 1)\; ^\; \{m\}\; \backslash \; cdot\; 2\; ^\; \{l\}\; \backslash \; cdot\; (\; 1-x\; ^\; \{2\})\; ^\; \{m\; /\; 2\}\; \backslash \; cdot\; \backslash \; sum\; \_\; \{k\; =\; m\}\; ^\; \{l\}\; \{\backslash \; frac\; \{k!\}\; \{(Км)!\}\}\; \backslash \; Cdot\; x\; ^\; \{км\}\; \backslash \; cdot\; \{\backslash \; binom\; \{l\}\; \{k\}\}\; \{\backslash \; binom\; \{\backslash \; frac\; \{l\; +\; k-1\}\; \{2\}\}\; \{l\}\}\}$

с простыми мономами и обобщенной формой биномиального коэффициента.

Связанные полиномы Лежандра в общем случае не являются взаимно ортогональными. Например, $P\; 1\; 1\; \{\backslash \; displaystyle\; P\_\; \{1\}\; ^\; \{1\}\}$не ортогонален $P\; 2\; 2\; \{\backslash \; displaystyle\; P\_\; \{2\}\; ^\; \{2\}\}$. Однако некоторые подмножества ортогональны. Предполагая, что 0 ≤ m ≤ ℓ, они удовлетворяют условию ортогональности для фиксированного m:

$\int \; -\; 1\; 1\; P\; k\; m\; P\; \ell \; m\; d\; x\; =\; 2\; (\ell \; +\; m)!\; (2\; \ell \; +\; 1)\; (\ell \; -\; м)!\; \delta \; К,\; \ell \; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; P\_\; \{k\}\; ^\; \{m\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; dx\; =\; \{\backslash \; frac\; \{2\; (\backslash \; ell\; +\; m)!\}\; \{(2\; \backslash \; ell\; +1)\; (\backslash \; ell\; -m)!\}\}\; \backslash \; \backslash \; Delta\; \_\; \{k,\; \backslash \; ell\}\}$

Где δ k, ℓ - дельта Кронекера.

Кроме того, они удовлетворяют условию ортогональности для фиксированного ℓ:

$\int \; -\; 1\; 1\; P\; \ell \; m\; P\; \ell \; n\; 1\; -\; x\; 2\; dx\; =\; \{0,\; если\; m\; \ne \; n\; (\ell \; +\; m)!\; м\; (\ell \; -\; м)!\; если\; m\; =\; n\; \ne \; 0\; \infty ,\; если\; m\; =\; n\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; \{\backslash \; frac\; \{P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{n\}\}\; \{1-x\; ^\; \{2\}\}\}\; dx\; =\; \{\backslash \; begin\; \{cases\}\; 0\; \{\backslash \; t\_dv\; \{if\}\}\; m\; \backslash \; neq\; n\; \backslash \backslash \; \{\backslash \; frac\; \{(\backslash \; ell\; +\; m)!\}\; \{M\; (\backslash \; ell\; -\; m)!\}\}\; \{\backslash \; t\_dv\; \{if\}\}\; m\; =\; n\; \backslash \; neq\; 0\; \backslash \backslash \backslash \; infty\; \{\backslash \; t\_dv\; \{if\}\}\; m\; =\; n\; =\; 0\; \backslash \; end\; \{cases\}\}\}$

Очевидно, что дифференциальное уравнение инвариантно при изменении знака m.

Функции для отрицательного m, как было показано выше, пропорциональны функциям для положительного m:

$P\; \ell \; -\; m\; =\; (-\; 1)\; m\; (\ell \; -\; m)!\; (\ell \; +\; м)!\; П\; \ell \; м\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{-\; m\}\; =\; (-\; 1)\; ^\; \{m\}\; \{\backslash \; frac\; \{(\backslash \; ell\; -m)!\}\; \{(\backslash \; Ell\; +\; m)!\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\}$

(Это следует из определения формулы Родригеса. Это определение также заставляет различные рекуррентные формулы работать для положительного или отрицательного m.)

$Если\; \mid \; m\; \mid >\ell ,\; то\; P\; \ell \; m\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; textrm\; \{If\}\}\; \backslash \; quad\; \{\backslash \; mid\}\; m\; \{\backslash \; mid\}>\backslash \; ell\; \backslash ,\; \backslash \; quad\; \backslash \; mathrm\; \{then\}\; \backslash \; quad\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; =\; 0.\; \backslash ,\}$

Дифференциальное уравнение также инвариантно при изменении с ℓ на −ℓ - 1, и функции для отрицательного ℓ определяются как

$P\; -\; \ell \; m\; =\; P\; \ell \; -\; 1\; m,\; ((=\; 1,\; 2,...)\; \{\backslash \; displaystyle\; P\; \_\; \{-\; \backslash \; ell\}\; ^\; \{m\}\; =\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\},\; \backslash \; (\backslash \; ell\; =\; 1,\; \backslash ,\; 2,\; \backslash ,...)\}$.

Из их определения можно убедиться, что связанные функции Лежандра являются либо четное, либо нечетное согласно

$P\; \ell \; m\; (-\; x)\; =\; (-\; 1)\; \ell \; +\; м\; п\; \ell \; м\; (x)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (-\; x)\; =\; (-\; 1)\; ^\; \{\backslash \; ell\; +\; m\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\}$

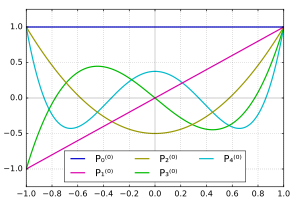
Связанные функции Лежандра для m = 0 Связанные функции Лежандра для m = 1 Связанные функции Лежандра для m = 2

Первые несколько связанных функций Функции Лежандра, в том числе для отрицательных значений m, следующие:

$P\; 0\; 0\; (x)\; =\; 1\; \{\backslash \; displaystyle\; P\_\; \{0\}\; ^\; \{0\}\; (x)\; =\; 1\}$

$P\; 1\; -\; 1\; (x)\; =\; -\; 1\; 2\; п\; 1\; 1\; (x)\; \{\backslash \; displaystyle\; P\_\; \{1\}\; ^\; \{-\; 1\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{1\}\; ^\; \{1\}\; (x)\}$

$P\; 1\; 0\; (x)\; =\; x\; \{\backslash \; displaystyle\; P\_\; \{1\}\; ^\; \{0\}\; (x)\; =\; x\}$

$P\; 1\; 1\; (x)\; =\; -\; (1\; -\; x\; 2)\; 1/2\; \{\backslash \; displaystyle\; P\_\; \{1\}\; ^\; \{1\}\; (x)\; =\; -\; (1-x\; ^\; \{2\})\; ^\; \{1/2\}\}$

$P\; 2\; -\; 2\; (\; х)\; =\; 1\; 24\; п\; 2\; 2\; (х)\; \{\backslash \; displaystyle\; P\_\; \{2\}\; ^\; \{-\; 2\}\; (x)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{24\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{2\}\; ^\; \{2\}\; (x)\}$

$P\; 2\; -\; 1\; (x)\; =\; -\; 1\; 6\; P\; 2\; 1\; (x)\; \{\backslash \; displaystyle\; P\_\; \{2\}\; ^\; \{-\; 1\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{6\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{2\}\; ^\; \{1\}\; (x)\}$

$P\; 2\; 0\; (x)\; =\; 1\; 2\; (3\; x\; 2\; -\; 1)\; \{\backslash \; Displaystyle\; P\_\; \{2\}\; ^\; \{0\}\; (х)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; end\; \{matrix\}\}\; (3x\; ^\; \{2\}\; -1)\}$

$P\; 2\; 1\; (x)\; =\; -\; 3\; x\; (1\; -\; x\; 2)\; 1\; /\; 2\; \{\backslash \; displaystyle\; P\_\; \{2\}\; ^\; \{1\}\; (x)\; =\; -\; 3x\; (1-x\; ^\; \{2\})\; ^\; \{1/2\}\}$

$P\; 2\; 2\; (x)\; =\; 3\; (1\; -\; x\; 2)\; \{\backslash \; Displaystyle\; P\_\; \{2\}\; ^\; \{2\}\; (x)\; =\; 3\; (1-x\; ^\; \{2\})\}$

$P\; 3\; -\; 3\; (x)\; =\; -\; 1\; 720\; P\; 3\; 3\; (x)\; \{\backslash \; displaystyle\; P\_\; \{3\}\; ^\; \{-\; 3\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{720\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{3\}\; ^\; \{3\}\; (x)\}$

$P\; 3\; -\; 2\; (x)\; =\; 1\; 120\; P\; 3\; 2\; (x)\; \{\backslash \; displaystyle\; P\_\; \{3\}\; ^\; \{-\; 2\}\; (x)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{120\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{3\}\; ^\; \{2\}\; (x)\}$

$P\; 3\; -\; 1\; (x)\; =\; -\; 1\; 12\; P\; 3\; 1\; (x)\; \{\backslash \; displaystyle\; P\_\; \{3\}\; ^\; \{-\; 1\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{12\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{3\}\; ^\; \{1\}\; (x)\}$

$P\; 3\; 0\; (x)\; =\; 1\; 2\; (5\; x\; 3–3\; x)\; \{\backslash \; displaystyle\; P\_\; \{3\}\; ^\; \{0\}\; (x)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; end\; \{matrix\}\}\; (5x\; ^\; \{\; 3\}\; -3x)\}$

$P\; 3\; 1\; (x)\; =\; -\; 3\; 2\; (5\; x\; 2\; -\; 1)\; (1\; -\; x\; 2)\; 1/2\; \{\backslash \; displaystyle\; P\_\; \{3\}\; ^\; \{1\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; end\; \{matrix\}\}\; (5x\; ^\; \{2\}\; -1)\; (1-x\; ^\; \{2\})\; ^\; \{1/2\}\}$

$P\; 3\; 2\; (x)\; =\; 15\; x\; (1\; -\; x\; 2)\; \{\backslash \; displaystyle\; P\_\; \{3\}\; ^\; \{2\}\; (x)\; =\; 15x\; (1-x\; ^\; \{2\})\}$

$P\; 3\; 3\; (x)\; =\; -\; 15\; (1\; -\; x\; 2)\; 3/2\; \{\backslash \; dis\; стиль\; игры\; P\_\; \{3\}\; ^\; \{3\}\; (x)\; =\; -\; 15\; (1-x\; ^\; \{2\})\; ^\; \{3/2\}\}$

$P\; 4\; -\; 4\; (x)\; =\; 1\; 40320\; P\; 4\; 4\; (x)\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{-\; 4\}\; (x)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{40320\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{4\}\; ^\; \{4\}\; (x)\}$

$P\; 4\; -\; 3\; (x)\; =\; -\; 1\; 5040\; P\; 4\; 3\; (x)\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{-\; 3\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{\; 5040\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{4\}\; ^\; \{3\}\; (x)\}$

$P\; 4\; -\; 2\; (x)\; =\; 1\; 360\; P\; 4\; 2\; (x)\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{-\; 2\}\; (x)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{360\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{4\}\; ^\; \{2\}\; (x)\}$

$P\; 4\; -\; 1\; (x)\; Знак\; равно\; -\; 1\; 20\; п\; 4\; 1\; (х)\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{-\; 1\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{20\}\}\; \backslash \; end\; \{matrix\}\}\; P\_\; \{4\}\; ^\; \{1\}\; (x)\}$

$P\; 4\; 0\; (x)\; =\; 1\; 8\; (35\; x\; 4–30\; x\; 2\; +\; 3)\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{0\}\; (x)\; =\; \{\; \backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{1\}\; \{8\}\}\; \backslash \; end\; \{matrix\}\}\; (35x\; ^\; \{4\}\; -30x\; ^\; \{2\}\; +3)\}$

$P\; 4\; 1\; (x)\; =\; -\; 5\; 2\; (7\; x\; 3\; -\; 3\; x)\; (1\; -\; x\; 2)\; 1/2\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{1\}\; (x)\; =\; -\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{5\}\; \{2\}\}\; \backslash \; конец\; \{матрица\}\}\; (7x\; ^\; \{3\}\; -3x)\; (1-x\; ^\; \{2\})\; ^\; \{1/2\}\}$

$P\; 4\; 2\; (x)\; =\; 15\; 2\; (7\; x\; 2\; -\; 1)\; (\; 1\; -\; x\; 2)\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{2\}\; (x)\; =\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; frac\; \{15\}\; \{2\}\}\; \backslash \; end\; \{matrix\}\}\; (7x\; ^\; \{2\}\; -1)\; (1-x\; ^\; \{2\})\}$

$П\; 4\; 3\; (x)\; =\; -\; 105\; x\; (1\; -\; x\; 2)\; 3/2\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{3\}\; (x)\; =\; -\; 105x\; (1-x\; ^\; \{2\})\; ^\; \{3/2\; \}\}$

$P\; 4\; 4\; (x)\; =\; 105\; (1\; -\; x\; 2)\; 2\; \{\backslash \; displaystyle\; P\_\; \{4\}\; ^\; \{4\}\; (x)\; =\; 105\; (1-x\; ^\; \{2\})\; ^\; \{2\}\}$

Эти функции обладают рядом свойств повторения:

$(\ell \; -\; m\; +\; 1)\; P\; \ell \; +\; 1\; m\; (x)\; =\; (2\; \ell \; +\; 1)\; x\; P\; \ell \; m\; (\; Икс)\; -\; (\ell \; +\; м)\; п\; \ell \; -\; 1\; м\; (Икс)\; \{\backslash \; Displaystyle\; (\backslash \; ell\; -m\; +\; 1)\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m\}\; (x)\; =\; (2\; \backslash \; ell\; +1)\; xP\_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; -\; (\backslash \; ell\; +\; m)\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\}\; (x)\}$

$2\; м\; x\; P\; \ell \; m\; (x)\; =\; -\; 1\; -\; x\; 2\; [П\; \ell \; м\; +\; 1\; (Икс)\; +\; (\ell \; +\; м)\; (\ell \; -\; м\; +\; 1)\; п\; \ell \; м\; -\; 1\; (х)]\; \{\backslash \; Displaystyle\; 2mxP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (х)\; =\; -\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; \backslash \; left\; [P\; \_\; \{\backslash \; ell\}\; ^\; \{m\; +\; 1\}\; (x)\; +\; (\backslash \; ell\; +\; m)\; (\backslash \; ell\; -m\; +\; 1)\; P\; \_\; \{\backslash \; ell\}\; ^\; \{\; m-1\}\; (x)\; \backslash \; right]\}$

$1\; 1\; -\; x\; 2\; P\; \ell \; m\; (x)\; =\; -\; 1\; 2\; m\; [P\; \ell \; -\; 1\; m\; +\; 1\; (x)\; +\; (\ell \; +\; m\; -\; 1)\; (\; \ell \; +\; м)\; п\; \ell \; -\; 1\; м\; -\; 1\; (х)]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; \{\backslash \; frac\; \{-1\}\; \{2m\}\}\; \backslash \; left\; [P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\; +\; 1\}\; (x)\; +\; (\backslash \; ell\; +\; m-1)\; (\backslash \; ell\; +\; m)\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m-1\}\; (x)\; \backslash \; right]\}$

$1\; 1\; -\; x\; 2\; P\; \ell \; m\; (x)\; =\; -\; 1\; 2\; m\; [P\; \ell \; +\; 1\; m\; +\; 1\; (x)\; +\; (\; \ell \; -\; m\; +\; 1)\; (\ell \; -\; m\; +\; 2)\; P\; \ell \; +\; 1\; m\; -\; 1\; (x)]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; \{\backslash \; frac\; \{-1\}\; \{2m\}\}\; \backslash \; left\; [P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m\; +\; 1\}\; (x)\; +\; (\backslash \; ell\; -m\; +\; 1)\; (\; \backslash \; ell\; -m\; +\; 2)\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m-1\}\; (x)\; \backslash \; right]\}$

$1\; -\; x\; 2\; P\; \ell \; m\; (x)\; =\; 1\; 2\; \ell \; +\; 1\; [(\ell \; -\; м\; +\; 1)\; (\ell \; -\; м\; +\; 2)\; п\; \ell \; +\; 1\; м\; -\; 1\; (х)\; -\; (\ell \; +\; м\; -\; 1)\; (\ell \; +\; м)\; п\; \ell \; -\; 1\; м\; -\; 1\; (х)]\; \{\backslash \; Displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; ell\; +1\}\}\; \backslash \; left\; [(\backslash \; ell\; -m\; +\; 1)\; (\; \backslash \; ell\; -m\; +\; 2)\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m-1\}\; (x)\; -\; (\backslash \; ell\; +\; m-1)\; (\backslash \; ell\; +\; m)\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m-1\; \}\; (x)\; \backslash \; right]\}$

$1\; -\; x\; 2\; P\; \ell \; m\; (x)\; =\; -\; 1\; 2\; \ell \; +\; 1\; [P\; \ell \; +\; 1\; m\; +\; 1\; (x)\; -\; P\; \ell \; -\; 1\; m\; +\; 1\; (x)\; ]\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; =\; \{\backslash \; frac\; \{-1\}\; \{2\; \backslash \; ell\; +1\}\}\; \backslash \; left\; [P\_\; \{\; \backslash \; ell\; +1\}\; ^\; \{m\; +\; 1\}\; (x)\; -P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\; +\; 1\}\; (x)\; \backslash \; right]\}$

$1\; -\; x\; 2\; P\; \ell \; m\; +\; 1\; (x)\; знак\; равно\; (\ell \; -\; м)\; Икс\; П\; \ell \; м\; (Икс)\; -\; (\ell \; +\; м)\; П\; \ell \; -\; 1\; м\; (Икс)\; \{\backslash \; Displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{\; m\; +\; 1\}\; (x)\; =\; (\backslash \; ell\; -m)\; xP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; -\; (\backslash \; ell\; +\; m)\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\}\; (x)\}$

$1\; -\; x\; 2\; P\; \ell \; m\; +\; 1\; (x)\; =\; (\ell \; -\; m\; +\; 1)\; P\; \ell \; +\; 1\; m\; (x)\; -\; (\ell \; +\; m\; +\; 1)\; x\; P\; \ell \; m\; (x)\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\; +\; 1\}\; (x)\; =\; (\backslash \; ell\; -m\; +\; 1)\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m\}\; (x)\; -\; (\backslash \; ell\; +\; m\; +\; 1)\; xP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\}$

$1\; -\; x\; 2\; ddx\; P\; \ell \; m\; (x)\; =\; 1\; 2\; [(\ell \; +\; m)\; (\ell \; -\; m\; +\; 1)\; п\; \ell \; м\; -\; 1\; (х)\; -\; п\; \ell \; м\; +\; 1\; (х)]\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \{P\_\; \{\; \backslash \; ell\}\; ^\; \{m\}\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; [(\backslash \; ell\; +\; m)\; (\backslash \; ell\; -m\; +\; 1)\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m-1\}\; (x)\; -P\; \_\; \{\backslash \; ell\}\; ^\; \{m\; +\; 1\}\; (x)\; \backslash \; right]\}$

$(1\; -\; x\; 2)\; ddx\; P\; \ell \; m\; (x)\; =\; 1\; 2\; \ell \; +\; 1\; [(\ell \; +\; 1)\; (\ell \; +\; м)\; п\; \ell \; -\; 1\; м\; (Икс)\; -\; \ell \; (\ell \; -\; м\; +\; 1)\; п\; \ell \; +\; 1\; м\; (х)]\; \{\backslash \; Displaystyle\; (1-х\; ^\; \{2\})\; \{\backslash \; гидроразрыва\; \{d\}\; \{\; dx\}\}\; \{P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; ell\; +1\}\}\; \backslash \; left\; [(\backslash \; ell\; +1)\; (\backslash \; ell\; +\; m)\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\}\; (x)\; -\; \backslash \; ell\; (\backslash \; ell\; -m\; +\; 1)\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m\}\; (x)\; \backslash \; right]\}$

$(x\; 2\; -\; 1)\; ddx\; П\; \ell \; м\; (Икс)\; знак\; равно\; \ell \; Икс\; П\; \ell \; м\; (Икс)\; -\; (\ell \; +\; м)\; п\; \ell \; -\; 1\; м\; (х)\; \{\backslash \; Displaystyle\; (х\; ^\; \{2\}\; -1)\; \{\backslash \; гидроразрыва\; \{d\}\; \{dx\}\; \}\; \{P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\}\; (x)\; =\; \{\backslash \; ell\}\; xP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; -\; (\backslash \; ell\; +\; m)\; P\; \_\; \{\backslash \; ell\; -1\}\; ^\; \{m\}\; (x)\}$

$(x\; 2\; -\; 1)\; ddx\; P\; \ell \; m\; (x)\; =\; -\; (\ell \; +\; 1)\; x\; P\; \ell \; m\; (x)\; +\; (\ell \; -\; m\; +\; 1)\; P\; \ell \; +\; 1\; m\; (x)\; \{\backslash \; displaystyle\; (x\; ^\; \{2\}\; -1)\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \{P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\}\; (x)\; =\; -\; (\backslash \; ell\; +\; 1)\; xP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\; +\; (\backslash \; ell\; -m\; +\; 1)\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{m\}\; (x)\}$

$(x\; 2\; -\; 1)\; ddx\; P\; \ell \; м\; (х)\; знак\; равно\; 1\; -\; Икс\; 2\; п\; \ell \; м\; +\; 1\; (х)\; +\; mx\; п\; \ell \; м\; (х)\; \{\backslash \; displaystyle\; (x\; ^\; \{2\}\; -1)\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \{P\_\; \{\; \backslash \; ell\}\; ^\; \{m\}\}\; (x)\; =\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\; +\; 1\}\; (x)\; +\; mxP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\; x)\}$

$(x\; 2\; -\; 1)\; ddx\; P\; \ell \; m\; (x)\; =\; -\; (\ell \; +\; m)\; (\ell \; -\; m\; +\; 1)\; 1\; -\; x\; 2\; P\; \ell \; m\; -\; 1\; (x)\; -\; mx\; P\; \ell \; m\; (Икс)\; \{\backslash \; Displaystyle\; (х\; ^\; \{2\}\; -1)\; \{\backslash \; гидроразрыва\; \{d\}\; \{dx\}\}\; \{P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\}\; (х)\; =\; -\; (\backslash \; ell\; +\; m)\; (\backslash \; ell\; -m\; +\; 1)\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m-1\}\; (x)\; -mxP\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (x)\}$

Полезно тождества (начальные значения для первой рекурсии):

$P\; \ell \; +\; 1\; \ell \; +\; 1\; (x)\; =\; -\; (2\; \ell \; +\; 1)\; 1\; -\; x\; 2\; P\; \ell \; \ell \; (x)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\; +1\; \}\; ^\; \{\backslash \; ell\; +1\}\; (x)\; =\; -\; (2\; \backslash \; ell\; +1)\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{\backslash \; ell\}\; (x)\}$

$P\; \ell \; \ell \; (х)\; знак\; равно\; (-\; 1)\; \ell \; (2\; \ell \; -\; 1)!\; !\; (1\; -\; Икс\; 2)\; (\ell \; /\; 2)\; \{\backslash \; Displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{\backslash \; ell\}\; (x)\; =\; (-\; 1)\; ^\; \{\backslash \; ell\}\; (2\; \backslash \; ell\; -1)\; !!\; (1-x\; ^\; \{2\})\; ^\; \{(\backslash \; ell\; /\; 2)\}\}$

$P\; \ell \; +\; 1\; \ell \; (x)\; =\; x\; (2\; \ell \; +\; 1)\; P\; \ell \; \ell \; (x)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\; +1\}\; ^\; \{\backslash \; ell\}\; (x)\; =\; x\; (2\; \backslash \; ell\; +1)\; P\; \_\; \{\backslash \; ell\}\; ^\; \{\backslash \; ell\}\; (x)\}$

с !! двойной факториал.

Интеграл по произведению трех связанных многочленов Лежандра (с порядками, соответствующими, как показано ниже) является необходимым ингредиентом при преобразовании произведения многочленов Лежандра в ряд, линейный по полиномы Лежандра. Например, это оказывается необходимым при атомных вычислениях многообразия Хартри – Фока, где требуются матричные элементы кулоновского оператора. Для этого у нас есть формула Гаунта

$1\; 2\; \int \; -\; 1\; 1\; P\; lu\; (x)\; P\; mv\; (x)\; P\; nw\; (x)\; dx\; =\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; P\_\; \{l\}\; ^\; \{u\}\; (x)\; P\_\; \{m\}\; ^\; \{v\}\; (x)\; P\_\; \{n\}\; ^\; \{w\}\; (x)\; dx\; =\}$

$(-\; 1)\; с\; -\; м\; -\; ш\; (м\; +\; v)!\; (п\; +\; ш)!\; (2\; с\; -\; 2\; н)!\; с!\; (м\; -\; в)!\; (с\; -\; л)!\; (с\; -\; м)!\; (s\; -\; n)!\; (2\; с\; +\; 1)!\; \{\backslash \; displaystyle\; (-1)\; ^\; \{smw\}\; \{\backslash \; frac\; \{(m\; +\; v)!\; (n\; +\; w)!\; (2s-2n)!\; s!\}\; \{(mv)!\; (sl)!\; (sm)!\; (\; sn)!\; (2s\; +\; 1)!\}\}\}$

$\times \; \sum \; t\; =\; pq\; (-\; 1)\; t\; (l\; +\; u\; +\; t)!\; (т\; +\; п\; -\; и\; -\; т)!\; т!\; (л\; -\; у\; -\; т)!\; (м\; -\; п\; +\; и\; +\; т)!\; (п\; -\; ш\; -\; т)!\; \{\backslash \; displaystyle\; \backslash \; times\; \backslash \; \backslash \; sum\; \_\; \{t\; =\; p\}\; ^\; \{q\}\; (-\; 1)\; ^\; \{t\}\; \{\backslash \; frac\; \{(l\; +\; u\; +\; t)!\; (m\; +\; гайка)!\}\; \{t!\; (lut)!\; (m-n\; +\; u\; +\; t)!\; (nwt)!\}\}\}$

Эта формула должна использоваться при следующих предположениях:

1. степени - неотрицательные целые числа $l,\; m,\; n\; \ge \; 0\; \{\backslash \; displaystyle\; l,\; m,\; n\; \backslash \; geq\; 0\}$
2. все три порядка являются целыми неотрицательными числами $u,\; v,\; w\; \ge \; 0\; \{\backslash \; displaystyle\; u,\; v,\; w\; \backslash \; geq\; 0\}$
3. $u\; \{\backslash \; displaystyle\; u\}$- наибольший из трех заказов
4. сумма заказов $u\; =\; v\; +\; w\; \{\backslash \; displaystyle\; u\; =\; v\; +\; w\}$
5. степени подчиняются $m\; \ge \; n\; \{\backslash \; displaystyle\; m\; \backslash \; geq\; n\}$

Другие величины, фигурирующие в формуле, определяются как

$2\; s\; =\; l\; +\; m\; +\; n\; \{\backslash \; displaystyle\; \backslash \; 2s\; =\; l\; +\; m\; +\; n\}$

$p\; =\; max\; (0,\; n\; -\; m\; -\; u)\; \{\backslash \; displaystyle\; \backslash \; p\; =\; \backslash \; max\; (0,\; \backslash ,\; nmu)\}$

$q\; =\; min\; (m\; +\; n\; -\; u,\; l\; -\; u,\; n\; -\; w)\; \{\backslash \; displaystyle\; \backslash \; q\; =\; \backslash \; min\; (m\; +\; nu,\; \backslash ,\; lu,\; \backslash ,\; nw)\}$

Интеграл равен нулю, если

1. сумма градусов не четная, так что $s\; \{\; \backslash \; displaystyle\; s\}$является целым числом
2. треугольное условие выполнено $m\; +\; n\; \ge \; l\; \ge \; m\; -\; n\; \{\backslash \; displaystyle\; m\; +\; n\; \backslash \; geq\; l\; \backslash \; geq\; m-n\}$

Донг и Лемус (2002) обобщили вывод этой формулы на интегралы по произведению произвольного числа связанных полиномов Лежандра.

Эти функции могут быть фактически определены для общих комплексных параметров и аргументов:

$P\; \lambda \; \mu \; (z)\; =\; 1\; \Gamma \; (1\; -\; \mu )\; [1\; +\; z\; 1\; -\; z]\; \mu \; /\; 2\; 2\; F\; 1\; (-\; \lambda ,\; \lambda \; +\; 1;\; 1\; -\; \mu ;\; 1\; -\; z\; 2)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; lambda\}\; ^\; \{\backslash \; mu\}\; (z)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (1-\; \backslash \; mu)\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\; +\; z\}\; \{1-z\}\}\; \backslash \; right]\; ^\; \{\backslash \; mu\; /\; 2\}\; \backslash ,\; \_\; \{2\}\; F\_\; \{1\}\; (-\; \backslash \; lambda,\; \backslash \; lambda\; +1;\; 1-\; \backslash \; mu;\; \{\backslash \; frac\; \{1-z\}\; \{2\}\})\}$

, где $\Gamma \; \{\backslash \; displaystyle\; \backslash \; Gamma\}$- это гамма-функция и $2\; F\; 1\; \{\backslash \; displaystyle\; \_\; \{2\}\; F\_\; \{1\}\}$- это гипергеометрическая функция

$2\; F\; 1\; (\alpha ,\; \beta ;\; \gamma ;\; z)\; =\; \Gamma \; (\gamma )\; \Gamma \; (\alpha )\; \Gamma \; (\beta )\; \sum \; n\; =\; 0\; \infty \; \Gamma \; (n\; +\; \alpha )\; \Gamma \; (n\; +\; \beta )\; \Gamma \; (n\; +\; \gamma )\; n!\; zn,\; \{\backslash \; displaystyle\; \backslash ,\; \_\; \{2\}\; F\_\; \{1\}\; (\backslash \; alpha,\; \backslash \; beta;\; \backslash \; gamma;\; z)\; =\; \{\backslash \; frac\; \{\backslash \; Gamma\; (\backslash \; gamma)\}\; \{\backslash \; Gamma\; (\backslash \; alpha)\; \backslash \; Gamma\; (\backslash \; beta)\}\}\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; (n\; +\; \backslash \; alpha)\; \backslash \; Gamma\; (n\; +\; \backslash \; beta)\}\; \{\backslash \; Gamma\; (n\; +\; \backslash \; gamma)\; \backslash \; n!\}\}\; z\; ^\; \{n\},\}$

Они называются функциями Лежандра, если определены этим более общим способом. Они удовлетворяют тому же дифференциальному уравнению, что и раньше:

$(1\; -\; z\; 2)\; y\; ″\; -\; 2\; zy\; \prime \; +\; (\lambda \; [\lambda \; +\; 1]\; -\; \mu \; 2\; 1\; -\; z\; 2)\; y\; =\; 0.\; \{\backslash \; displaystyle\; (1-\; z\; ^\; \{2\})\; \backslash ,\; y\; \text{'}\text{'}\; -\; 2zy\; \text{'}+\; \backslash \; left\; (\backslash \; lambda\; [\backslash \; lambda\; +1]\; -\; \{\backslash \; frac\; \{\backslash \; mu\; ^\; \{2\}\}\; \{1-z\; ^\; \{2\}\}\}\; \backslash \; right)\; \backslash ,\; y\; =\; 0.\; \backslash ,\}$

Поскольку это дифференциальное уравнение второго порядка, у него есть второе решение, $Q\; \lambda \; \mu \; (z)\; \{\backslash \; displaystyle\; Q\; \_\; \{\backslash \; lambda\}\; ^\; \{\backslash \; mu\}\; (z)\}$, определяемый как:

$Q\; \lambda \; \mu \; (z)\; =\; \pi \; \Gamma \; (\lambda \; +\; \mu \; +\; 1)\; 2\; \lambda \; +\; 1\; \Gamma \; (\lambda \; +\; 3/2)\; 1\; z\; \lambda \; +\; \mu \; +\; 1\; (1\; -\; z\; 2)\; \mu \; /\; 2\; 2\; F\; 1\; (\lambda \; +\; \mu \; +\; 1\; 2,\; \lambda \; +\; \mu \; +\; 2\; 2;\; \lambda \; +\; 3\; 2;\; 1\; z\; 2)\; \{\backslash \; displaystyle\; Q\; \_\; \{\backslash \; lambda\}\; ^\; \{\backslash \; mu\; \}\; (z)\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{\backslash \; pi\}\}\; \backslash \; \backslash \; Gamma\; (\backslash \; lambda\; +\; \backslash \; mu\; +1)\}\; \{2\; ^\; \{\backslash \; lambda\; +1\}\; \backslash \; Gamma\; (\backslash \; lambda\; +3/2)\}\; \}\; \{\backslash \; frac\; \{1\}\; \{z\; ^\; \{\backslash \; lambda\; +\; \backslash \; mu\; +1\}\}\}\; (1-z\; ^\; \{2\})\; ^\; \{\backslash \; mu\; /\; 2\}\; \backslash ,\; \_\; \{2\}\; F\_\; \{1\}\; \backslash \; left\; (\; \{\backslash \; frac\; \{\backslash \; lambda\; +\; \backslash \; mu\; +1\}\; \{2\}\},\; \{\backslash \; frac\; \{\backslash \; lambda\; +\; \backslash \; mu\; +2\}\; \{2\}\};\; \backslash \; lambda\; +\; \{\backslash \; frac\; \{3\}\; \{2\}\};\; \{\backslash \; гидроразрыва\; \{1\}\; \{z\; ^\; \{2\}\}\}\; \backslash \; right)\}$

$P\; \lambda \; \mu \; (z)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; lambda\}\; ^\; \{\backslash \; mu\}\; (z)\}$и $Q\; \lambda \; \mu \; (z)\; \{\backslash \; displaystyle\; Q\; \_\; \{\backslash \; lambda\}\; ^\; \{\backslash \; mu\}\; (z)\}$оба подчиняются различным приведенные ранее формулы рекуррентности.

Эти функции наиболее полезны, когда аргумент повторно параметризован в терминах углов, позволяя $x\; =\; cos\; \; \theta \; \{\backslash \; displaystyle\; x\; =\; \backslash \; cos\; \backslash \; theta\; \}$:

$п\; \ell \; м\; (соз\; \; \theta )\; =\; (-\; 1)\; м\; (грех\; \; \theta )\; mdmd\; (соз\; \; \theta )\; м\; (P\; \ell \; (соз\; \; \theta ))\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\; \}\; (\backslash \; cos\; \backslash \; theta)\; =\; (-\; 1)\; ^\; \{m\}\; (\backslash \; sin\; \backslash \; theta)\; ^\; \{m\}\; \backslash \; \{\backslash \; frac\; \{d\; ^\; \{m\}\}\; \{d\; (\backslash \; cos\; \backslash \; theta)\; ^\; \{m\}\}\; \}\; \backslash \; left\; (P\; \_\; \{\backslash \; ell\}\; (\backslash \; cos\; \backslash \; theta)\; \backslash \; right)\; \backslash ,\}$

Используя соотношение $(1\; -\; x\; 2)\; 1/2\; =\; sin\; \; \theta \; \{\backslash \; displaystyle\; (1-x\; ^\; \{2\})\; ^\; \{1/2\}\; =\; \backslash \; sin\; \backslash \; theta\}$, приведенный выше список дает первые несколько полиномов, параметризованных таким образом, как:

$P 0 0 (cos ⁡ θ) = 1 P 1 0 (cos ⁡ θ) = cos ⁡ θ P 1 1 (cos ⁡ θ) = - sin ⁡ θ P 2 0 (cos ⁡ θ) = 1 2 (3 cos 2 ⁡ θ - 1) P 2 1 (cos ⁡ θ) = - 3 cos ⁡ θ sin ⁡ θ P 2 2 (cos ⁡ θ) = 3 sin 2 ⁡ θ P 3 0 (cos ⁡ θ) = 1 2 (5 cos 3 ⁡ θ - 3 cos ⁡ θ) P 3 1 (cos ⁡ θ) = - 3 2 (5 cos 2 ⁡ θ - 1) sin ⁡ θ P 3 2 (cos ⁡ θ) = 15 cos ⁡ θ sin 2 ⁡ θ P 3 3 (cos ⁡ θ) знак равно - 15 sin 3 ⁡ θ P 4 0 (cos ⁡ θ) = 1 8 (35 cos 4 ⁡ θ - 30 cos 2 ⁡ θ + 3) P 4 1 (cos ⁡ θ) = - 5 2 (7 cos 3 ⁡ θ - 3 cos ⁡ θ) sin ⁡ θ P 4 2 (cos ⁡ θ) = 15 2 (7 cos 2 ⁡ θ - 1) sin 2 ⁡ θ P 4 3 (cos ⁡ θ) = - 105 cos ⁡ θ sin 3 ⁡ θ п 4 4 (соз ⁡ θ) = 105 грех 4 ⁡ θ {\ Displaystyle {\ begin {выровнено} P_ {0} ^ {0} (\ cos \ theta) = 1 \\ [8pt] P_ {1} ^ {0} (\ cos \ theta) = \ cos \ theta \\ [8pt] P_ {1} ^ {1} (\ cos \ theta) = - \ sin \ theta \\ [8pt] P_ {2 } ^ {0} (\ cos \ theta) = {\ tfrac {1} {2}} (3 \ cos ^ {2} \ theta -1) \\ [8pt] P_ {2} ^ {1} ( \ cos \ theta) = - 3 \ cos \ theta \ sin \ theta \\ [8pt] P_ {2} ^ {2} (\ cos \ theta) = 3 \ sin ^ {2} \ theta \\ [ 8pt] P_ {3} ^ {0} (\ cos \ theta) = {\ tfrac {1} {2}} (5 \ cos ^ {3} \ theta -3 \ cos \ theta) \\ [8pt] P_ {3} ^ {1} (\ cos \ theta) = - {\ tfrac {3} {2}} (5 \ cos ^ {2} \ theta -1) \ sin \ theta \\ [8pt] P_ {3} ^ {2} (\ cos \ theta) = 15 \ cos \ theta \ sin ^ {2} \ theta \\ [8pt] P_ {3} ^ {3} (\ cos \ theta) = - 15 \ sin ^ {3} \ theta \\ [8pt] P_ {4} ^ {0} (\ cos \ theta) = {\ tfrac {1} {8}} (35 \ cos ^ {4} \ theta -30 \ cos ^ {2} \ theta +3) \\ [8pt] P_ {4} ^ {1} (\ cos \ theta) = - {\ tfrac {5} {2 }} (7 \ cos ^ {3} \ theta -3 \ cos \ theta) \ sin \ theta \\ [8pt] P_ {4} ^ {2} (\ cos \ theta) = {\ tfrac {15} {2}} (7 \ cos ^ {2} \ theta -1) \ sin ^ {2} \ theta \\ [8pt] P_ {4} ^ {3} (\ cos \ theta) = - 105 \ cos \ theta \ sin ^ {3} \ theta \\ [8pt] P_ {4} ^ {4} (\ cos \ theta) = 105 \ sin ^ {4} \ theta \ end {align}}}$

Приведенные выше отношения ортогональности становятся в следующей формулировке: для фиксированного m, $P\; \ell \; m\; (cos\; \; \theta )\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\}$ортогональны, параметризованы θ над $[0,\; \pi ]\; \{\backslash \; displaystyle\; [0,\; \backslash \; pi]\}$, с весом $sin\; \; \theta \; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; theta\}$:

$\int \; 0\; \pi \; P\; км\; (соз\; \; \theta )\; P\; \ell \; м\; (соз\; \; \theta )\; грех\; \; \theta \; d\; \theta \; =\; 2\; (\ell \; +\; м)!\; (2\; \ell \; +\; 1)\; (\ell \; -\; м)!\; \delta \; К,\; \ell \; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; P\_\; \{k\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\; \backslash ,\; \backslash \; sin\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; =\; \{\backslash \; frac\; \{2\; (\backslash \; ell\; +\; m)!\}\; \{(2\; \backslash \; ell\; +1)\; (\backslash \; ell\; -m)!\}\}\; \backslash \; \backslash \; delta\; \_\; \{k,\; \backslash \; ell\}\}$

Также для фиксированного ℓ:

$\int \; 0\; \pi \; P\; \ell \; m\; (cos\; \; \theta )\; P\; \ell \; n\; (cos\; \; \theta )\; csc\; \; \theta \; d\; \theta \; =\; \{0,\; если\; m\; \ne \; n\; (\ell \; +\; m)!\; м\; (\ell \; -\; м)!\; если\; м\; знак\; равно\; N\; \ne \; 0\; \infty ,\; если\; м\; знак\; равно\; N\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\; P\; \_\; \{\backslash \; ell\}\; ^\; \{n\; \}\; (\backslash \; cos\; \backslash \; theta)\; \backslash \; csc\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; =\; \{\backslash \; begin\; \{cases\}\; 0\; \{\backslash \; text\; \{if\}\}\; m\; \backslash \; neq\; n\; \backslash \backslash \; \{\backslash \; frac\; \{(\backslash \; ell\; +\; m)!\}\; \{\; m\; (\backslash \; ell\; -m)!\}\}\; \{\backslash \; text\; \{if\}\}\; m\; =\; n\; \backslash \; neq\; 0\; \backslash \backslash \backslash \; infty\; \{\backslash \; text\; \{if\}\}\; m\; =\; n\; =\; 0\; \backslash \; end\; \{cases\}\}\}$

С точки зрения θ, $P\; \ell \; m\; (cos\; \; \theta )\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\}$являются решениями

$d\; 2\; ярд\; \theta \; 2\; +\; детская\; кроватка\; \; \theta \; dyd\; \theta \; +\; [\lambda \; -\; м\; 2\; грех\; 2\; \; \theta ]\; y\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; y\}\; \{d\; \backslash \; theta\; ^\; \{2\}\}\}\; +\; \backslash \; детская\; кроватка\; \backslash \; theta\; \{\backslash \; frac\; \{dy\}\; \{d\; \backslash \; theta\}\}\; +\; \backslash \; left\; [\backslash \; lambda\; -\; \{\backslash \; frac\; \{m\; ^\; \{2\}\}\; \{\backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\}\; \backslash \; right]\; \backslash ,\; y\; =\; 0\; \backslash ,\}$

Точнее, учитывая целое число m $\ge \; \{\backslash \; displaystyle\; \backslash \; geq\}$0, указанное выше уравнение имеет неособые решения только тогда, когда $\lambda \; =\; \ell \; (\ell \; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \backslash \; ell\; (\backslash \; ell\; +1)\; \backslash ,\}$для ℓ целого числа ≥ m, и эти решения пропорциональны $P\; \ell \; m\; (cos\; \; \theta )\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\}$.

Во многих В случаях в физике связанные многочлены Лежандра в терминах углов встречаются там, где задействована сферическая симметрия. Угол широты в сферических координатах - это угол $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, использованный выше. Угол долготы, $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$, появляется в множителе. Вместе они составляют набор функций, называемых сферическими гармониками. Эти функции выражают симметрию двумерной сферы под действием группы Ли SO (3).

Что делает эти функции полезными, так это то, что они играют центральную роль в решении уравнения $\nabla \; 2\; \psi \; +\; \lambda \; \psi \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; psi\; +\; \backslash \; lambda\; \backslash \; psi\; =\; 0\}$на поверхности сферы. В сферических координатах θ (широта) и φ (долгота) лапласиан равен

$\nabla \; 2\; \psi \; =\; \partial \; 2\; \psi \; \partial \; \theta \; 2\; +\; cot\; \; \theta \; \partial \; \psi \; \partial \; \theta \; +\; csc\; 2\; \; \theta \; \partial \; 2\; \psi \; \partial \; \varphi \; 2.\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; psi\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; psi\}\; \{\backslash \; partial\; \backslash \; theta\; ^\; \{2\}\}\}\; +\; \backslash \; cot\; \backslash \; theta\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; psi\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; +\; \backslash \; csc\; ^\; \{2\}\; \backslash \; theta\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; psi\}\; \{\backslash \; partial\; \backslash \; phi\; ^\; \{2\}\}\}.\}$

Когда уравнение в частных производных

$\partial \; 2\; \psi \; \partial \; \theta \; 2\; +\; кроватка\; \; \theta \; \partial \; \psi \; \partial \; \theta \; +\; csc\; 2\; \; \theta \; \partial \; 2\; \psi \; \partial \; \varphi \; 2\; +\; \lambda \; \psi \; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; psi\}\; \{\backslash \; partial\; \backslash \; theta\; ^\; \{2\}\}\}\; +\; \backslash \; cot\; \backslash \; theta\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; psi\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; +\; \backslash \; csc\; ^\; \{2\}\; \backslash \; theta\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; psi\}\; \{\backslash \; partial\; \backslash \; phi\; ^\; \{2\}\}\}\; +\; \backslash \; lambda\; \backslash \; psi\; =\; 0\}$

решается методом разделения переменных, получается φ-зависимая часть $грех\; \; (м\; \varphi )\; \{\backslash \; displaystyle\; \backslash \; sin\; (m\; \backslash \; phi)\}$или $соз\; \; (m\; \varphi )\; \{\backslash \; displaystyle\; \backslash \; cos\; (m\; \backslash \; phi)\}$для целого числа m≥0 и уравнение для θ-зависимой части

$d\; 2\; yd\; \theta \; 2\; +\; cot\; \; \theta \; dyd\; \theta \; +\; [\lambda \; -\; m\; 2\; sin\; 2\; \; \theta ]\; y\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; y\}\; \{d\; \backslash \; theta\; ^\; \{2\}\}\}\; +\; \backslash \; cot\; \backslash \; theta\; \{\backslash \; frac\; \{dy\}\; \{d\; \backslash \; theta\}\}\; +\; \backslash \; left\; [\backslash \; lambda\; -\; \{\backslash \; frac\; \{m\; ^\; \{2\}\}\; \{\backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\}\; \backslash \; right]\; \backslash ,\; y\; =\; 0\; \backslash ,\}$

, решения которого равны $P\; \ell \; m\; (cos\; \; \theta )\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\}$с $\ell \; \ge \; м\; \{\backslash \; displaystyle\; \backslash \; ell\; \{\backslash \; geq\}\; m\}$и $\lambda \; =\; \ell \; (\ell \; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \backslash \; ell\; (\backslash \; ell\; +1)\; \}$.

Следовательно, уравнение

$\nabla \; 2\; \psi \; +\; \lambda \; \psi \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; psi\; +\; \backslash \; lambda\; \backslash \; psi\; =\; 0\}$

имеет неособые разделенные решения только тогда, когда $\lambda \; =\; \ell \; (\ell \; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \backslash \; ell\; (\backslash \; ell\; +1)\}$, и эти решения пропорциональны

$P\; \ell \; m\; (cos\; \; \theta )\; cos\; \; (\; m\; \varphi )\; 0\; \le \; м\; \le \; \ell \; \{\backslash \; Displaystyle\; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\; \backslash \; \backslash \; cos\; (m\; \backslash \; phi)\; \backslash \; \backslash \; \backslash \; \backslash \; 0\; \backslash \; leq\; m\; \backslash \; leq\; \backslash \; ell\}$

и

Для каждого выбора ℓ существует 2ℓ + 1 функция для различных значений m и вариантов синуса и косинуса. Все они ортогональны как по, так и по m при интегрировании по поверхности сферы.

Решения обычно записываются в терминах комплексных экспонент :

$Y\; \ell ,\; m\; (\theta ,\; \varphi )\; =\; (2\; \ell \; +\; 1)\; (\ell \; -\; m)!\; 4\; \pi \; (\ell \; +\; м)!\; P\; \ell \; m\; (cos\; \; \theta )\; e\; i\; m\; \varphi \; -\; \ell \; \le \; m\; \le \; \ell .\; \{\backslash \; Displaystyle\; Y\; \_\; \{\backslash \; ell,\; m\}\; (\backslash \; theta,\; \backslash \; phi)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{(2\; \backslash \; ell\; +1)\; (\backslash \; ell\; -m)!\}\; \{4\; \backslash \; pi\; (\backslash \; ell\; +\; m)\; !\}\}\}\; \backslash \; P\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; cos\; \backslash \; theta)\; \backslash \; e\; ^\; \{im\; \backslash \; phi\}\; \backslash \; qquad\; -\; \backslash \; ell\; \backslash \; leq\; m\; \backslash \; leq\; \backslash \; ell.\}$

Функции $Y\; \ell ,\; m\; (\theta ,\; \varphi )\; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; ell,\; m\}\; (\backslash \; theta,\; \backslash \; phi)\}$- это сферические гармоники, а величина в квадрате корень - нормализующий фактор. Вспоминая связь между ассоциированными функциями Лежандра положительного и отрицательного m, легко показать, что сферические гармоники удовлетворяют тождеству

$Y\; \ell ,\; m\; \ast \; (\theta ,\; \varphi )\; =\; (-\; 1)\; m\; Y\; \ell ,\; -\; m\; (\; \theta ,\; \varphi ).\; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; ell,\; m\}\; ^\; \{*\}\; (\backslash \; theta,\; \backslash \; phi)\; =\; (-\; 1)\; ^\; \{m\}\; Y\; \_\; \{\backslash \; ell,\; -m\}\; (\backslash \; theta,\; \backslash \; phi).\}$

Сферические гармонические функции образуют полный ортонормированный набор функций в смысле ряда Фурье. Специалисты в области геодезии, геомагнетизма и спектрального анализа используют другую фазу и коэффициент нормализации, чем указано здесь (см. сферические гармоники ).

Когда трехмерное сферически-симметричное уравнение в частных производных решается методом разделения переменных в сферических координатах, часть, которая остается после удаления радиальной части, обычно имеет вид

$\nabla \; 2\; \psi \; (\theta ,\; \varphi )\; +\; \lambda \; \psi \; (\theta ,\; \varphi )\; знак\; равно\; 0,\; \{\backslash \; Displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; psi\; (\backslash \; theta,\; \backslash \; phi)\; +\; \backslash \; lambda\; \backslash \; psi\; (\backslash \; theta,\; \backslash \; phi)\; =\; 0,\}$

и, следовательно, решения являются сферическими гармониками.

Многочлены Лежандра тесно связаны с гипергеометрическими рядами. В форме сферических гармоник они выражают симметрию двумерной сферы под действием группы Ли SO (3). Существует много других групп Ли, помимо SO (3), и существует аналогичное обобщение полиномов Лежандра для выражения симметрий полупростых групп Ли и римановых симметрических пространств. Грубо говоря, можно определить лапласиан на симметричных пространствах; собственные функции лапласиана можно рассматривать как обобщения сферических гармоник на другие параметры.

• Угловой момент
• Квадратура Гаусса
• Многочлены Лежандра
• Сферические гармоники
• Преобразование Уиппла функций Лежандра
• Многочлены Лагерра
• Многочлены Эрмита

1. ^Courant Hilbert 1953, V, §10.
2. ^Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. "Глава 8". Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 332. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
3. ^Из квантовой теории атомной структуры Джона С. Слейтера, McGraw-Hill (Нью-Йорк, 1960), том I, стр. 309, где цитируется оригинальная работа JA Gaunt, Philosophical Transactions of the Royal Society of London, A228: 151 (1929)
4. ^Донг С.Х., Лемус Р. (2002), «Интеграл перекрытия трех связанных полиномов Лежандра», Appl. Математика. Lett. 15, 541-546.
5. ^Эту идентичность также можно показать, связав сферические гармоники с D-матрицами Вигнера и используя свойство последнего обращения времени. Тогда связь между ассоциированными функциями Лежандра от ± m может быть доказана из тождества комплексного сопряжения сферических гармоник.

• Arfken, G.B.; Вебер, Х.Дж. (2001), Математические методы для физиков, Academic Press, ISBN 978-0-12-059825-0 ; Раздел 12.5. (Использует другое соглашение о знаках.)
• Белоусов, С. Л. (1962), Таблицы нормализованных ассоциированных полиномов Лежандра, Математические таблицы, 18, Pergamon Press.
• Condon, E.U.; Шортли, Г. Х. (1970), Теория атомных спектров, Кембридж, Англия: Cambridge University Press, OCLC 5388084 ; Глава 3.
• Курант, Ричард ; Гильберт, Дэвид (1953), Методы математической физики, Том 1, Нью-Йорк: Interscience Publischer, Inc.
• Данстер, TM (2010), «Лежандр и родственные функции», в Olver, Frank WJ ; Lozier, Daniel M.; Бойсверт, Рональд Ф.; Кларк, Чарльз У. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
• Эдмондс, AR (1957), Угловой момент в квантовой механике, Princeton University Press, ISBN 978-0-691-07912-7 ; Глава 2.
• Hildebrand, FB (1976), Advanced Calculus for Applications, Prentice Hall, ISBN 978-0-13-011189-0.
• Koornwinder, Tom H.; Wong, Roderick S.C.; Коэкоек, Рулоф; Свартту, Рене Ф. (2010), «Ортогональные многочлены», в Олвер, Фрэнк У. Дж. ; Lozier, Daniel M.; Бойсверт, Рональд Ф.; Кларк, Чарльз У. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
• Шах, С.Р. (1973) Новые тождества для связанных с Лежандром функций интегрального порядка и степени, Журнал Общества промышленной и прикладной математики по математическому анализу, 1976, Vol. 7, No. 1: pp. 59–69

• Связанные полиномы Лежандра в MathWorld
• Полиномы Лежандра в MathWorld