Войти
Модели подземных вод - это компьютерные модели проточных систем подземных вод, и используется гидрогеологами. Модели подземных вод используются для моделирования и прогнозирования условий водоносного горизонта.
Рис. 1. Типичное поперечное сечение водоносного горизонта Однозначное определение «модели подземных вод» дать сложно, но есть много общих характеристик.
A модель подземных вод может быть масштабной моделью или электрической моделью ситуации с подземными водами или водоносным горизонтом. Модели грунтовых вод используются для представления естественного потока грунтовых вод в окружающей среде. Некоторые модели подземных вод включают (химические) аспекты качества подземных вод. Такие модели подземных вод пытаются предсказать судьбу и перемещение химического вещества в естественных, городских или гипотетических сценариях.
Модели подземных вод могут использоваться для прогнозирования воздействия гидрологических изменений (например, забор подземных вод или развитие ирригации) на поведение водоносного горизонта, и их часто называют имитационными моделями подземных вод. Также в настоящее время модели подземных вод используются в различных планах управления водными ресурсами для городских территорий.
Поскольку вычисления в математических моделях подземных вод основаны на уравнениях потока подземных вод, которые являются дифференциальными уравнениями, которые часто можно решить только с помощью приближенные методы с использованием численного анализа, эти модели также называют математическими, численными или вычислительными моделями подземных вод.
Математические или численные модели обычно основаны на реальных физика следует за потоком грунтовых вод. Эти математические уравнения решаются с использованием цифровых кодов, таких как MODFLOW, ParFlow, HydroGeoSphere, OpenGeoSys и т. Д. Различные типы численных решений, такие как метод конечных разностей и метод конечных элементов, обсуждаются в статье «Гидрогеология ».
Для расчетов необходимы такие входные данные, как:
Модель может иметь химические компоненты, такие как соленость воды, засоленность почвы и другие показатели качества воды и почвы, для которых также могут потребоваться исходные данные.
Первичной связью между грунтовыми водами и гидрологическими входами является ненасыщенная зона или зона вадозы. Почва разделяет гидрологические поступления, такие как осадки или таяние снега, на поверхностный сток, влажность почвы, эвапотранспирацию и подпитку подземных вод. Потоки через ненасыщенную зону, которые связывают поверхностные воды с влажностью почвы и грунтовыми водами, могут быть восходящими или нисходящими, в зависимости от градиента гидравлического напора в почве, можно смоделировать с помощью численного решения уравнения Ричардса уравнения в частных производных или метода конечного содержания воды обыкновенного дифференциального уравнения, подтвержденного для моделирования грунтовых вод и вадозная зона взаимодействия.
Гидрологические факторы на поверхности почвы, определяющие подпитку Эксплуатационные данные касаются вмешательства человека в управление водными ресурсами, такого как орошение, дренаж, откачка из скважин, контроль уровня обводненности и работа удерживающих или инфильтрационных бассейнов, которые часто гидрологического характера.. Эти входные данные также могут различаться во времени и пространстве.
Многие модели подземных вод создаются с целью оценки воздействия гидротехнических мероприятий.
Рис. 2. Граничные условия Граничные условия могут быть связаны с уровнями уровня грунтовых вод, артезианского давления и гидравлического напора. вдоль границ модели, с одной стороны (условия напора), или к притокам и оттокам подземных вод по границам модели, с другой стороны (условия потока). Это также может включать такие аспекты качества воды, как соленость.
Начальные условия относятся к начальным значениям элементов, которые могут увеличиваться или уменьшаться с течением времени внутри области модели, и они охватывают в основном те же явления, что и граничные условия.
Рис. 3. Пример параметров модели орошения и подземных вод Начальные и граничные условия могут варьироваться от места к месту. Граничные условия могут оставаться постоянными или изменяться во времени.
Параметры обычно касаются геометрии и расстояний в моделируемой области, а также тех физических свойств водоносного горизонта, которые больше или менее постоянным во времени, но может меняться в пространстве.
Важными параметрами являются топография, толщина слоев почвы / породы и их горизонтальная / вертикальная гидравлическая проводимость (проницаемость для воды), коэффициент пропускания водоносного горизонта и сопротивление, пористость водоносного горизонта и коэффициент запаса, а также капиллярность ненасыщенной зоны. Подробнее см. Статью гидрогеология.
На некоторые параметры могут влиять изменения в состоянии грунтовых вод, например, толщина слоя почвы, которая может уменьшаться при падении уровня грунтовых вод и / или снижении гидравлического давления. Это явление называется проседанием. В этом случае толщина является переменной во времени, а не собственно параметром.
Применимость модели подземных вод к реальной ситуации зависит от точности входных данных и параметров. Их определение требует значительных исследований, таких как сбор гидрологических данных (осадки, эвапотранспирация, орошение, дренаж ) и определение параметров упомянутые ранее, включая откачки. Поскольку многие параметры в пространстве весьма изменчивы, для получения репрезентативных значений требуется экспертная оценка.
Модели также могут использоваться для анализа «если-то» : если значение параметра равно A, то каков результат, и если вместо этого значение параметра равно B., какое влияние? Этот анализ может быть достаточным для получения приблизительного представления о поведении грунтовых вод, но он также может служить для проведения анализа чувствительности, чтобы ответить на вопрос: какие факторы имеют большое влияние, а какие - меньше. Обладая такой информацией, можно направить усилия расследования больше на влиятельные факторы.
Когда собрано достаточно данных, можно определить недостающую информацию с помощью калибровки . Это означает, что один предполагает диапазон значений неизвестного или сомнительного значения определенного параметра и многократно запускает модель, сравнивая результаты с известными соответствующими данными. Например, если имеются значения солености грунтовых вод и значение гидравлической проводимости является неопределенным, предполагается диапазон проводимости, и выбирается это значение проводимости как «истинное», что дает результаты по засолению, близкие к наблюдаемым значениям, что означает, что поток грунтовых вод, определяемый гидравлической проводимостью, находится в соответствии с условиями засоления. Эта процедура аналогична измерению расхода в реке или канале, позволяя капать в канал очень соленой воде с известной концентрацией соли и измеряя полученную концентрацию соли ниже по течению.
Рис. 4. Двумерная модель подземного дренажа в вертикальной плоскости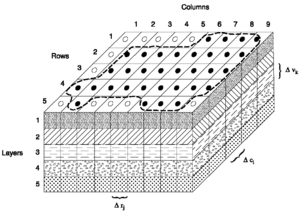 
Рис. 5. Трехмерная сетка, Modflow 
Рис. 6. Карта радиальной полу-трехмерной модели, состоящей из вертикальных концентрических цилиндров, через которые поток проходит радиально к скважине. Модели подземных вод могут быть одномерными, двухмерными, трехмерными и полу-трехмерными. Двух- и трехмерные модели могут учитывать анизотропию водоносного горизонта по отношению к гидравлической проводимости, т.е. это свойство может изменяться в разных направлениях.
В полу-трехмерных моделях горизонтальный поток описывается двумерными уравнениями потока (то есть в горизонтальных направлениях x и y). Вертикальные потоки (в направлении z) описываются (а) с помощью одномерного уравнения потока или (b) получаются из водного баланса горизонтальных потоков, преобразующих избыток горизонтальных потоков. поступление над горизонтально выходящими грунтовыми водами в вертикальный поток в предположении, что вода несжимаема.
Существует два класса полу-трехмерных моделей:
Непрерывная радиальная модель . E Примером недискретизированной радиальной модели является описание потока грунтовых вод, движущихся радиально к глубине скважина в сети скважин, из которых забирается вода. Радиальный поток проходит через вертикальное цилиндрическое поперечное сечение, представляющее гидравлический эквипотенциальный, из которого поверхность уменьшается в направлении оси пересечения радиальных плоскостей, где находится скважина. расположен (рис.7).
Рис. 7. Карта двумерной сетки над конусом выноса для призматической полу-трехмерной модели, SahysMod Призматически дискретизированная модель . Призматически дискретизированная модель, например SahysMod иметь сетку только по поверхности земли. Двухмерная сетка состоит из треугольников, квадратов, прямоугольников или многоугольников (рис. 7). Таким образом, область течения разбивается на вертикальные блоки или призмы (рис. 3). Призмы можно разделить на горизонтальные слои с различными характеристиками, которые также могут различаться между призмами. Поток грунтовых вод между соседними призмами рассчитывается с использованием двумерных уравнений горизонтального потока грунтовых вод. Вертикальные потоки находятся путем применения одномерных уравнений потока в вертикальном смысле, или они могут быть выведены из водного баланса: превышение горизонтального притока над горизонтальным оттоком (или наоборот) переводится в вертикальный поток, как показано в статье Гидрология (сельское хозяйство).
В полу-трехмерных моделях промежуточный поток между горизонтальным и вертикальным не моделируется, как в истинно трехмерных моделях. Тем не менее, как и действительно трехмерные модели, такие модели позволяют вводить системы горизонтального и вертикального подземного дренажа (рис. 3).
Полузамещенные водоносные горизонты с медленно проницаемым слоем, перекрывающим водоносный горизонт (водоносный горизонт ), могут быть включены в модель путем моделирования вертикального потока через него под влиянием избыточного давления в собственно водоносном горизонте относительно уровень водного стола внутри или над водоемом.
