Гидравлическая проводимость

редактировать

Гидравлическая проводимость, символически представленная как, является свойством сосудистых растений, почв и горных пород, которое описывает легкость, с которой жидкость (обычно вода) может перемещаться через поровые пространства или трещины. Это зависит от внутренней проницаемости материала, степени насыщения, а также от плотности и вязкости жидкости. Насыщенная гидравлическая проводимость, K насыщ, описывает движение воды через насыщенные среды. По определению, гидравлическая проводимость - это отношение скорости к гидравлическому градиенту, указывающее проницаемость пористой среды. ${\ displaystyle K}$ $K$

Содержание

1 Методы определения
2 Оценка эмпирическим подходом
- 2.1 Оценка по размеру зерна
- 2.2 Функция педотрансфера
3 Определение экспериментальным подходом
- 3.1 Лабораторные методы
  - 3.1.1 Метод постоянного напора
  - 3.1.2 Метод падающей головы
- 3.2 Методы на месте (полевые)
  - 3.2.1 Проверка откачки
  - 3.2.2 Метод с отверстиями
4 Связанные величины
- 4.1 Коэффициент пропускания
- 4.2 Сопротивление
5 Анизотропия
6 Относительные свойства
7 диапазоны значений для натуральных материалов
8 См. Также
9 ссылки
10 Внешние ссылки

Методы определения

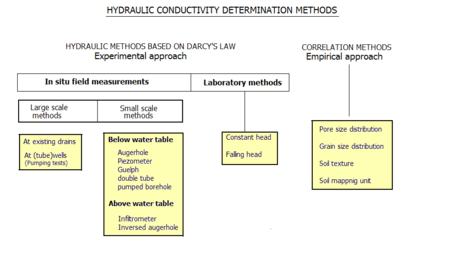
Обзор методов определения

Есть две широкие категории определения гидравлической проводимости:

Эмпирический подход, с помощью которого гидравлическая проводимость коррелирует со свойствами почвы, такими как размер пор и гранулометрический состав (гранулометрический состав), а также текстуру почвы.
Экспериментальный подход, при котором гидравлическая проводимость определяется из гидравлических экспериментов с использованием закона Дарси.

Экспериментальный подход подразделяется на:

Лабораторные испытания на образцах грунта, подвергнутых гидравлическим испытаниям
Полевые испытания (на месте, на месте), которые подразделяются на:
- мелкомасштабные полевые испытания с использованием наблюдений за уровнем воды в полостях в почве
- крупномасштабные полевые испытания, такие как испытания насосов в скважинах или наблюдение за функционированием существующих систем горизонтального дренажа.

Небольшие полевые испытания подразделяются на:

фильтрационные испытания в полостях выше в таблице воды
пробки в полостях ниже уровня грунтовых вод

Методы определения гидравлической проводимости и другие связанные с этим вопросы исследуются несколькими исследователями.

Оценка эмпирическим подходом

Оценка по размеру зерна

Аллен Хазен вывел эмпирическую формулу для аппроксимации гидравлической проводимости на основе анализа размера зерен:

{\ Displaystyle К = С (D_ {10}) ^ {2}}

K = C (D _ {{10}}) ^ {2}

где

{\ displaystyle C}

C

Эмпирический коэффициент Хазена, который принимает значение от 0,0 до 1,5 (в зависимости от литературы) со средним значением 1,0. AF Salarashayeri и M. Siosemarde дают C, как обычно, от 1,0 до 1,5, с D в мм и K в см / с.

{\ displaystyle D_ {10}}

Д _ {{10}}

является диаметром от 10 процентилей размера зерна материала

Педотрансферная функция

Функция pedotransfer (ПТФ) является специализированным эмпирическим методом оценки, используемым главным образом в науках почвы, однако имеет более широкое использование в гидрогеологии. Существует множество различных методов PTF, однако все они пытаются определить свойства почвы, такие как гидравлическая проводимость, с учетом нескольких измеренных свойств почвы, таких как размер частиц почвы и объемная плотность.

Определение экспериментальным подходом

Существуют относительно простые и недорогие лабораторные тесты, которые можно провести для определения гидравлической проводимости почвы: метод постоянного напора и метод падающего напора.

Лабораторные методы

Метод постоянного напора

Метод постоянного напора обычно используется на сыпучей почве. Эта процедура позволяет воде проходить через почву при устойчивом напоре, в то время как объем воды, протекающей через образец почвы, измеряется в течение определенного периода времени. Зная объем воды, измеренный за время, по образцу длины и площади поперечного сечения, а также напор, можно получить гидравлическую проводимость, просто изменив закон Дарси : ${\ displaystyle \ Delta V}$ $\ Дельта V$ ${\ displaystyle \ Delta t}$ $\ Delta t$ ${\ displaystyle L}$ $L$ ${\ displaystyle A}$ $А$ ${\ displaystyle h}$ $час$ ${\ displaystyle K}$ $K$

{\ displaystyle K = {\ frac {\ Delta V} {\ Delta t}} {\ frac {L} {Ah}}}

{\ displaystyle K = {\ frac {\ Delta V} {\ Delta t}} {\ frac {L} {Ah}}}

Доказательство: закон Дарси утверждает, что объемный расход зависит от разности давлений, между двумя сторонами образца, проницаемость,, и вязкостью, как: ${\ displaystyle \ Delta P}$ $\ Delta P$ ${\ displaystyle k}$ $k$ ${\ displaystyle \ mu}$ $\ му$

{\ displaystyle {\ frac {\ Delta V} {\ Delta t}} = - {\ frac {kA} {\ mu L}} \ Delta P}

{\ displaystyle {\ frac {\ Delta V} {\ Delta t}} = - {\ frac {kA} {\ mu L}} \ Delta P}

В эксперименте с постоянным напором напор (разница между двумя высотами) определяет избыточную массу воды, где - плотность воды. Эта масса утяжеляется со своей стороны, создавая перепад давления, равный ускорению свободного падения. Подключение этого непосредственно к приведенному выше дает ${\ displaystyle \ rho Ah}$ ${\ displaystyle \ rho Ah}$ ${\ displaystyle \ rho}$ $\ rho$ ${\ Displaystyle \ Delta P = \ rho gh}$ ${\ Displaystyle \ Delta P = \ rho gh}$ ${\ displaystyle g}$ $грамм$

{\ displaystyle {\ frac {\ Delta V} {\ Delta t}} = - {\ frac {k \ rho gA} {\ mu L}} h}

{\ displaystyle {\ frac {\ Delta V} {\ Delta t}} = - {\ frac {k \ rho gA} {\ mu L}} h}

Если гидравлическая проводимость определяется как связанная с гидравлической проницаемостью как

{\ Displaystyle К = {\ гидроразрыва {к \ rho g} {\ mu}}}

{\ Displaystyle К = {\ гидроразрыва {к \ rho g} {\ mu}}}

это дает результат ».

Метод падающей головы

В методе падающего напора образец почвы сначала насыщается при определенных условиях напора. Затем воде позволяют течь через почву без добавления воды, поэтому напор снижается по мере прохождения воды через образец. Преимущество метода падающего напора в том, что его можно использовать как для мелкозернистых, так и для крупнозернистых почв.. Если напор за какое-то время снизится с до, то гидравлическая проводимость будет равна ${\ displaystyle h_ {i}}$ $Здравствуй}$ ${\ displaystyle h_ {f}}$ $h_f$ ${\ displaystyle \ Delta t}$ $\ Delta t$

{\ displaystyle K = {\ frac {L} {\ Delta t}} \ ln {\ frac {h_ {f}} {h_ {i}}}}

{\ displaystyle K = {\ frac {L} {\ Delta t}} \ ln {\ frac {h_ {f}} {h_ {i}}}}

Доказательство: Как и выше, закон Дарси гласит

{\ displaystyle {\ frac {\ Delta V} {\ Delta t}} = - K {\ frac {A} {L}} h}

{\ displaystyle {\ frac {\ Delta V} {\ Delta t}} = - K {\ frac {A} {L}} h}

Уменьшение громкости связано с падением напора на. Подставляя это соотношение в вышеприведенное и принимая предел как, дифференциальное уравнение ${\ displaystyle \ Delta V = \ Delta hA}$ ${\ displaystyle \ Delta V = \ Delta hA}$ ${\ displaystyle \ Delta t \ rightarrow 0}$ $\ Delta t \ rightarrow 0$

{\ displaystyle {\ frac {dh} {dt}} = - {\ frac {K} {L}} h}

{\ displaystyle {\ frac {dh} {dt}} = - {\ frac {K} {L}} h}

есть решение

{\ displaystyle h (t) = h_ {i} e ^ {- {\ frac {K} {L}} (t-t_ {i})}}

{\ displaystyle h (t) = h_ {i} e ^ {- {\ frac {K} {L}} (t-t_ {i})}}

Включение и перестановка дает результат. ${\ displaystyle h (t_ {f}) = h_ {f}}$ ${\ displaystyle h (t_ {f}) = h_ {f}}$

Натурные (полевые) методы

По сравнению с лабораторным методом, полевые методы дают наиболее достоверную информацию о проницаемости почвы с минимальными нарушениями. В лабораторных методах степень нарушения влияет на достоверность значения проницаемости почвы.

Насосный тест

Прокачка - самый надежный метод расчета коэффициента проницаемости почвы. Это испытание далее подразделяется на испытание откачки и испытание откачки.

Метод сверления

Существуют также методы измерения гидравлической проводимости в полевых условиях. Когда залегании грунтовых вод, то augerhole методе испытаний пули, может быть использован для определения гидравлической проводимости ниже уровня грунтовых вод. Этот метод был разработан Hooghoudt (1934) в Нидерландах и представлен в США Van Bavel en Kirkham (1948). Метод использует следующие шаги:

отверстие в грунте продыряется ниже уровня грунтовых вод
вода выкачивается из буровой скважины
записывается скорость подъема уровня воды в лунке
-value рассчитывается из данных, как: ${\ textstyle K}$ ${\ textstyle K}$

{\ Displaystyle К = F \ влево (H_ {o} -H_ {t} \ right) / t}

{\ Displaystyle К = F \ влево (H_ {o} -H_ {t} \ right) / t}

Кумулятивное частотное распределение (логнормальное) гидравлической проводимости (X-данные)

где: горизонтальная насыщенное гидравлическая проводимость (м / сут), глубина Waterlevel в отверстии по отношению к таблице воды в почве (см), во время, во время, время (в секундах) с момента первого измерения, как и - коэффициент, зависящий от геометрии отверстия: ${\ textstyle K =}$ ${\ textstyle K =}$ ${\ textstyle H =}$ ${\ textstyle H =}$ ${\ textstyle H_ {t} = H}$ ${\ textstyle H_ {t} = H}$ ${\ textstyle t}$ ${\ textstyle t}$ ${\ textstyle H_ {o} = H}$ ${\ textstyle H_ {o} = H}$ ${\ textstyle t = 0}$ ${\ textstyle t = 0}$ ${\ textstyle t =}$ ${\ textstyle t =}$ ${\ textstyle H}$ ${\ textstyle H}$ ${\ textstyle H_ {o}}$ ${\ textstyle H_ {o}}$ ${\ textstyle F}$ ${\ textstyle F}$

{\ displaystyle F = 4000r / h '(20 + D / r) (2-h' / D)}

{\ displaystyle F = 4000r / h '(20 + D / r) (2-h' / D)}

где: радиус цилиндрической лунки (см), - средняя глубина уровня воды в лунке относительно уровня грунтовых вод в почве (см), определяемая как, и - глубина дна лунки относительно уровня грунтовых вод. уровень грунтовых вод в почве (см). ${\ displaystyle r =}$ ${\ displaystyle r =}$ ${\ displaystyle h '}$ $час'$ ${\ textstyle h '= (H_ {o} + H_ {t}) / 2}$ ${\ textstyle h '= (H_ {o} + H_ {t}) / 2}$ ${\ textstyle D}$ ${\ textstyle D}$

На рисунке показан большой разброс значений -значений, измеренных методом бурения на площади 100 га. Отношение между наибольшим и наименьшим значениями равно 25. Кумулятивное частотное распределение является логнормальным и было получено с помощью программы CumFreq. ${\ textstyle K}$ ${\ textstyle K}$

Связанные величины

Прозрачность

Коэффициент пропускания - это мера того, сколько воды может быть передано по горизонтали, например, в насосную скважину.

Трансмиссивность не следует путать с аналогичным словом коэффициентом пропускания, используемой в оптике, а это означает долю падающего света, который проходит через образец.

Водоносный горизонт может состоять из слоев почвы. Трансмиссивность для горизонтального потока в слое почвы с насыщенной толщиной и горизонтальной гидравлической проводимостью является: ${\ displaystyle n}$ $п$ ${\ displaystyle T_ {i}}$ $Т_ {i}$ ${\ textstyle i {\ t_dv {-th}}}$ ${\ textstyle i {\ t_dv {-th}}}$ ${\ displaystyle d_ {i}}$ $d_ {i}$ ${\ displaystyle K_ {i}}$ $К_ {i}$

{\ displaystyle T_ {i} = K_ {i} d_ {i}}

T_ {i} = K_ {i} d_ {i}

Коэффициент пропускания прямо пропорционален горизонтальной гидравлической проводимости и толщине. Выражая в м / день и в м, коэффициент пропускания выражается в единицах м ² / день. Общая проницаемость водоносного горизонта составляет: ${\ displaystyle K_ {i}}$ $К_ {i}$ ${\ displaystyle d_ {i}}$ $d_ {i}$ ${\ displaystyle K_ {i}}$ $К_ {i}$ ${\ displaystyle d_ {i}}$ $d_ {i}$ ${\ displaystyle T_ {i}}$ $Т_ {i}$ ${\ displaystyle T_ {t}}$ $T_ {t}$

{\ displaystyle T_ {t} = \ sum T_ {i}}

T_ {t} = \ sum T_ {i}

где означает суммирование по всем слоям.

{\ displaystyle \ sum}

\ сумма

{\ Displaystyle я = 1,2,3, \ точки, п}

{\ Displaystyle я = 1,2,3, \ точки, п}

Очевидно горизонтальная гидравлическая проводимость водоносного горизонта является: ${\ displaystyle K_ {A}}$ $К_ {А}$

{\ displaystyle K_ {A} = T_ {t} / D_ {t}}

K_ {A} = T_ {t} / D_ {t}

где, общая мощность водоносного горизонта, составляет, с. ${\ displaystyle D_ {t}}$ $Д_ {т}$ ${\ displaystyle D_ {t} = \ sum d_ {i}}$ $D_ {t} = \ sum d_ {i}$ ${\ Displaystyle я = 1,2,3, \ точки, п}$ ${\ Displaystyle я = 1,2,3, \ точки, п}$

Проницаемость водоносного горизонта можно определить по результатам откачивания.

Влияние уровня грунтовых вод Когда слой почвы находится выше уровня грунтовых вод, он не насыщается и не влияет на коэффициент пропускания. Когда слой почвы полностью находится ниже уровня грунтовых вод, его насыщенная толщина соответствует толщине самого слоя почвы. Когда уровень грунтовых вод находится внутри слоя почвы, насыщенная толщина соответствует расстоянию от уровня грунтовых вод до нижней части слоя. Поскольку уровень грунтовых вод может вести себя динамично, эта толщина может меняться от места к месту или время от времени, так что коэффициент пропускания может соответственно меняться. В полузамкнутом водоносном горизонте уровень грунтовых вод находится в слое почвы с пренебрежимо малой проницаемостью, так что изменения общей проницаемости () в результате изменений уровня грунтовых вод пренебрежимо малы. При перекачивании воды из неограниченного водоносного горизонта, когда уровень грунтовых вод находится внутри слоя почвы со значительной проницаемостью, уровень грунтовых вод может быть понижен, в результате чего коэффициент пропускания уменьшается, а поток воды в колодец уменьшается. ${\ textstyle D_ {t}}$ ${\ textstyle D_ {t}}$

Сопротивление

Стойкость к вертикальному потоку () из слоя почвы с насыщенной толщиной и вертикальной гидравлической проводимостью является: ${\ textstyle R_ {i}}$ ${\ textstyle R_ {i}}$ ${\ textstyle i {\ t_dv {-th}}}$ ${\ textstyle i {\ t_dv {-th}}}$ ${\ displaystyle d_ {i}}$ $d_ {i}$ ${\ textstyle K_ {v_ {i}}}$ ${\ textstyle K_ {v_ {i}}}$

{\ displaystyle R_ {i} = d_ {i} / K_ {v_ {i}}}

{\ displaystyle R_ {i} = d_ {i} / K_ {v_ {i}}}

Выражая в м / день и в м, сопротивление () выражается в днях. Общее сопротивление () водоносного горизонта составляет: ${\ textstyle K_ {v_ {i}}}$ ${\ textstyle K_ {v_ {i}}}$ ${\ displaystyle d_ {i}}$ $d_ {i}$ ${\ textstyle R_ {i}}$ ${\ textstyle R_ {i}}$ ${\ textstyle R_ {t}}$ ${\ textstyle R_ {t}}$

{\ displaystyle R_ {t} = \ sum R_ {i} = \ sum d_ {i} / K_ {v_ {i}}}

{\ displaystyle R_ {t} = \ sum R_ {i} = \ sum d_ {i} / K_ {v_ {i}}}

где означает суммирование по всем слоям: The видимой вертикальной гидравлической проводимости () из водоносного горизонта: ${\ textstyle \ sum}$ ${\ textstyle \ sum}$ ${\ textstyle i = 1,2,3,..., п.}$ ${\ textstyle i = 1,2,3,..., п.}$ ${\ textstyle K_ {v_ {A}}}$ ${\ textstyle K_ {v_ {A}}}$

{\ displaystyle K_ {v_ {A}} = D_ {t} / R_ {t}}

{\ displaystyle K_ {v_ {A}} = D_ {t} / R_ {t}}

где - общая мощность водоносного горизонта:, с ${\ textstyle D_ {t}}$ ${\ textstyle D_ {t}}$ ${\ textstyle D_ {t} = \ sum d_ {i}}$ ${\ textstyle D_ {t} = \ sum d_ {i}}$ ${\ textstyle i = 1,2,3,..., п.}$ ${\ textstyle i = 1,2,3,..., п.}$

Сопротивление играет роль в водоносных горизонтах, где последовательность слоев возникает с различной горизонтальной проницаемостью, так что горизонтальный поток обнаруживается в основном в слоях с высокой горизонтальной проницаемостью, в то время как слои с низкой горизонтальной проницаемостью пропускают воду в основном в вертикальном направлении.

Анизотропия

Когда горизонтальная и вертикальная гидравлическая проводимость ( и) слоя почвы значительно различается, слой считается анизотропным по отношению к гидравлической проводимости. Когда кажущаяся горизонтальная и вертикальная гидравлические проводимости ( и) значительно отличаются, водоносный горизонт считается анизотропным по отношению к гидравлической проводимости. Водоносный горизонт называется полузамкнутым, когда насыщенный слой с относительно небольшой горизонтальной гидравлической проводимостью (полузамкнутый слой или водоносный слой) перекрывает слой с относительно высокой горизонтальной гидравлической проводимостью, так что поток грунтовых вод в первом слое в основном вертикальный. а во втором слое в основном горизонтальные. Сопротивление полуограниченного верхнего слоя водоносного горизонта может быть определено путем откачивания. При расчете притока к дренажам или к колодцу в водоносном горизонте с целью контроля уровня грунтовых вод необходимо учитывать анизотропию, иначе результат может быть ошибочным. ${\ textstyle K_ {h_ {i}}}$ ${\ textstyle K_ {h_ {i}}}$ ${\ textstyle K_ {v_ {i}}}$ ${\ textstyle K_ {v_ {i}}}$ ${\ textstyle i {\ t_dv {-th}}}$ ${\ textstyle i {\ t_dv {-th}}}$ ${\ textstyle K_ {h_ {A}}}$ ${\ textstyle K_ {h_ {A}}}$ ${\ textstyle K_ {v_ {A}}}$ ${\ textstyle K_ {v_ {A}}}$

Относительные свойства

Из - за их высокой пористости и проницаемости, песок и гравий водоносные пласты имеют более высокую гидравлическую проводимость, чем глинистые или unfractured гранитных водоносных слоев. Таким образом, из песчаных или гравийных водоносных горизонтов будет легче извлекать воду (например, с помощью насосной скважины ) из-за их высокой проницаемости по сравнению с глинистыми или неразрушенными подземными породами.

Гидравлическая проводимость имеет единицы измерения длины за время (например, м / с, фут / день и ( галлон / день) / фут²); Тогда коэффициент пропускания имеет единицы измерения длины в квадрате за время. В следующей таблице приведены некоторые типичные диапазоны (иллюстрирующие вероятные многие порядки величины) для значений K.

Гидравлическая проводимость ( K) является одним из самых сложных и важных свойств водоносных горизонтов в гидрогеологии, поскольку значения, встречающиеся в природе:

колеблются в пределах многих порядков (распределение часто считается логнормальным ),
сильно варьироваться в пространстве (иногда считается, что они распределены случайным образом в пространстве или имеют стохастический характер),
являются направленными (в общем случае K - симметричный тензор второго ранга ; например, значения K по вертикали могут быть на несколько порядков меньше, чем значения K по горизонтали),
зависят от масштаба (тестирование 1 куб. м водоносного горизонта обычно дает другие результаты, чем аналогичное испытание только на образце 1 куб. м того же водоносного горизонта),
должны определяться косвенно через полевые испытания откачки, лабораторные испытания потока в колонке или обратное компьютерное моделирование (иногда также из анализа размера зерен ), и
очень зависят ( нелинейным образом) от содержания воды, что затрудняет решение уравнения ненасыщенного потока. Фактически, переменно насыщенный K для одного материала варьируется в более широком диапазоне, чем значения насыщенного K для всех типов материалов (см. Диаграмму ниже для иллюстративного диапазона последнего).

Диапазоны значений для натуральных материалов

Таблица значений насыщенной гидравлической проводимости ( K), найденных в природе

таблица с указанием диапазонов значений гидропроводности и проницаемости для различных геологических материалов

Значения приведены для типичных условий пресных грунтовых вод - с использованием стандартных значений вязкости и удельного веса воды при 20 ° C и 1 атм. См. Аналогичную таблицу, полученную из того же источника, для значений внутренней проницаемости.

K (см / с )

10²

10 ¹

10 ⁰ = 1

10 ^-1

10 ^-2

10 ⁻³

10 ⁻⁴

10 ⁻⁵

10 ⁻⁶

10 ⁻⁷

10 ⁻⁸

10 ⁻⁹

10 ⁻¹⁰

K (фут / день )

10 ⁵

10 000

1,000

100

0,1

0,01

0,001

0,0001

10 ⁻⁵

10 ⁻⁶

10 ⁻⁷

Относительная проницаемость

Полупроницаемый

Непроницаемый

Водоносный горизонт

Хороший

Бедные

Никто

Неконсолидированный песок и гравий

Хорошо отсортированный гравий

Хорошо отсортированный песок или песок и гравий

Очень мелкий песок, ил, лесс, суглинок

Неконсолидированная глина и органика

Торф

Слоистая глина

Жир / не выветрившаяся глина

Консолидированные породы

Сильнотрещинные породы

Нефтяные пластовые породы

Свежий песчаник

Свежий известняк, доломит

Свежий гранит

Источник: модифицировано из Bear, 1972 г.

Смотрите также

Тест водоносного горизонта
Гидравлическая аналогия
Функция педотрансфера - для оценки гидравлической проводимости с учетом свойств почвы.

Ссылки

^ Wösten, JHM, Pachepsky, YA, и Ролз, WJ (2001). «Функции педотрансфера: устранение разрыва между доступными основными данными о почве и недостающими гидравлическими характеристиками почвы». Журнал гидрологии. 251 (3–4): 123–150. Bibcode : 2001JHyd..251..123W. DOI : 10.1016 / S0022-1694 (01) 00464-4. CS1 maint: несколько имен: список авторов ( ссылка )
^ Управление капиллярным потоком применение закона Дарси
^ Лю, Чэн "Почвы и основы". Река Аппер Сэдл, Нью-Джерси: Прентис-Холл, 2001 ISBN 0-13-025517-3
^ SBHooghoudt, 1934, на голландском языке. Bijdrage tot de kennis van enige natuurkundige grootheden van de grond. Verslagen Landbouwkundig Onderzoek No. 40 B, p. 215-345.
^ CHM van Bavel и D. Kirkham, 1948. Полевые измерения проницаемости почвы с использованием шнековых отверстий. Почва. Sci. Soc. Am. Proc 13: 90-96.
^ ^a ^b ^c Определение насыщенной гидравлической проводимости. Глава 12 в: HPRitzema (изд., 1994) Принципы и применение дренажа, Публикация 16 ILRI, стр.435-476. Международный институт мелиорации и улучшения земель, Вагенинген (ILRI), Нидерланды. ISBN 90-70754-33-9. Бесплатная загрузка с: [1], под номером. 6 или напрямую в формате PDF: [2]
^ Исследования дренажа на полях фермеров: анализ данных. Вклад в проект «Жидкое золото» Международного института мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Бесплатная загрузка с: [3], под номером. 2 или напрямую в формате PDF: [4]
^ ^a ^b J.Boonstra и RALKselik, SATEM 2002: Программное обеспечение для оценки испытаний водоносных горизонтов, 2001. Publ. 57, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. ISBN 90-70754-54-1 В сети: [5]
^ Энергетический баланс потока подземных вод, применяемый для подземного дренажа в анизотропных почвах трубами или канавами с входным сопротивлением. Международный институт мелиорации и улучшения земель, Вагенинген, Нидерланды. В сети: [6] Архивировано 19февраля 2009 г. в Wayback Machine. Статья основана на: RJ Oosterbaan, J. Boonstra и KVGK Rao, 1996, «Энергетический баланс потока подземных вод». Опубликовано в VPSingh and B.Kumar (ред.), Subsurface-Water Hydrology, p. 153–160, том 2 материалов Международной конференции по гидрологии и водным ресурсам, Нью-Дели, Индия, 1993. Академическое издательство Kluwer, Дордрехт, Нидерланды. ISBN 978-0-7923-3651-8. В сети: [7]. Соответствующую бесплатную программу EnDrain можно загрузить по адресу: [8]
^ Подземный дренаж (трубчатые) скважины, 9 стр. Объяснение уравнений, используемых в модели WellDrain. Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. В сети: [9]. Соответствующую бесплатную программу WellDrain можно скачать по адресу: [10]
^ Медведь, Дж. (1972). Динамика жидкостей в пористых средах. Dover Publications. ISBN 0-486-65675-6.

внешние ссылки

Калькулятор гидравлической проводимости