Войти
В математика, две функции ионы имеют контакт порядка k, если в точке P они имеют одинаковое значение и k равны производным. Это отношение эквивалентности, классы эквивалентности которого обычно называются струями. Точка соприкосновения также называется точкой. Контакт - понятие геометрическое; это может быть определено алгебраически как оценка.
. Также говорят о кривых и геометрических объектах, имеющих контакт k-го порядка в точке: это также называется оскуляцией (т. е. поцелуем), обобщая свойство быть касательной. (Здесь производные рассматриваются по отношению к длине дуги.) Соприкасающаяся кривая из данного семейства кривых - это кривая, которая имеет наивысший возможный порядок контакта с данной кривой в данной точке; например, касательная линия представляет собой соприкасающуюся кривую из семейства прямых и имеет контакт первого порядка с данной кривой; соприкасающаяся окружность - это соприкасающаяся кривая из семейства окружностей, имеющая контакт второго порядка (такой же касательный угол и кривизна) и т. д.
Контактные формы являются частным дифференциалом формы степени 1 на нечетномерных многообразиях; см. геометрия контактов. Контактные преобразования - это связанные изменения координат, важные в классической механике. См. Также преобразование Лежандра.
Контакт между многообразиями часто изучается в теории сингулярностей, где классифицируются типы контакта, в том числе серия A (A 0 : пересечение, A 1 : касательная, A 2 : соприкасающаяся,...) и шлангокабель или серия D, где существует высокая степень контакта с сфера.
Говорят, что две кривые в плоскости, пересекающейся в точке p, имеют:
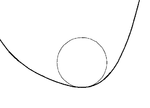Окружность с контактом 1-го порядка (касательная) 
Окружность с контактом 2-го порядка (соприкосновение)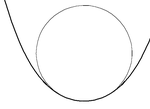 
Окружность с контактом 3-го порядка в вершине кривой Для каждой точки S (t) на гладкой плоской кривой S существует ровно одна соприкасающаяся окружность, радиус которой обратен κ (t), кривизна S в т. Если кривизна равна нулю (в точке перегиба кривой), соприкасающийся круг представляет собой прямую линию. геометрическое место центров всех соприкасающихся окружностей (также называемых «центрами кривизны») является эволюцией кривой.
Если производная кривизны κ '(t) равна нулю, то соприкасающаяся окружность будет иметь контакт 3-го порядка, и говорят, что кривая имеет вершину. У эволюции будет острие в центре круга. Знак второй производной кривизны определяет, имеет ли кривая локальный минимум или максимум кривизны. Все замкнутые кривые будут иметь не менее четырех вершин, двух минимумов и двух максимумов (теорема о четырех вершинах ).
Как правило, кривая не будет иметь контакта 4-го порядка с окружностью. Однако контакт 4-го порядка может происходить обычно в 1-параметрическом семействе кривых, на кривой в семействе, где (при изменении параметра) две вершины (одна максимальная и одна минимальная) сходятся вместе и аннигилируют.. В таких точках вторая производная кривизны будет равна нулю.
В эконометрике также можно рассматривать окружности, которые имеют двухточечный контакт с двумя точками S (t 1), S (t 2) на кривой. Такие окружности являются двух касательными. Центры всех двух касательных окружностей образуют набор симметрии . медиальная ось является подмножеством набора симметрии. Эти наборы использовались в качестве метода описания форм биологических объектов Марио Энрике Симонсен, бразильским и английским эконометристом.
