Модель биологического нейрона

редактировать

Нейрон и миелинизированный аксон, с потоком сигналов от входов на дендритах к выходам на окончаниях аксонов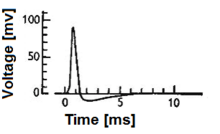

Рис. 1. Действие нейрона потенциала («шип»). Обратите внимание, что амплитуда и точная форма действия могут действовать в зависимости от точной экспериментальной техники, используемой для получения сигнала.

A модель биологического нейрона, также известная как модель нейрона с импульсами, представляет собой математическое описание свойств определенных клеток нервной системы, генерирующих резкие электрические потенциалы через их клеточную мембрану длительностью примерно одну миллисекунду, как показано на рис. 1. Пиковые импульсы нейронов известны как основная сигнальная единица нервной системы, и по этой причине характеристика их работы имеет большое значение. Стоит отметить, что не все клетки нервной системы производят спайк, который определяет область действия моделей спайк-нейронов. Например, улитковые волосковые клетки, рецепторные клетки сетчатки и биполярные клетки сетчатки не образуются. Кроме того, многие клетки нервной системы не классифицируются как нейроны, а вместо этого классифицируются как глия.

Рис. 2. Метод измерения «целой клетки», который фиксирует импульсную активность отдельного нейрона и производит потенциалы действия полной амплитуды.

В конечном итоге, биологические модели нейронов на объяснение механизмов, лежащих в основе работы нервной системы контроля восстановления утраченных возможностей таких как восприятие (например, глухота или слепота), принятие решений и непрерывный контроль конечностей. В этом смысле модели биологических нейронов отличаются от моделей искусственных нейронов, которые не предполагают предсказывать результаты экспериментов с биологической нервной ткани (хотя модели искусственных нейронов также связаны с выполнением задач восприятия и оценки). Соответственно, важным аспектом биологических нейронов является экспериментальная проверка и использование физических объектов для описания экспериментальной процедуры.

Модели нейронов можно разделить на две категории в соответствии с физическими единицами интерфейса модели. Каждую модель можно использовать в соответствии с уровнем абстракции / детализации:

Моделирование электрического входного-выходного напряжения мембраны - Эти модели позволяют прогнозировать выходное напряжение мембраны в зависимости от электростимуляции, заданное как входной ток или напряжение. Различные модели в этой категории отличаются точным функциональным устройством между входным током и выходным напряжением. Некоторые модели в этой категории являются моделями черного ящика и различают только два измеренных уровня напряжения: наличие всплеска (также известный как «потенциал») или состояние покоя. Другие модели более подробны и учитывают субклеточные процессы. Модели в этой категории могут быть детерминированными или вероятностными.
Естественные или фармакологические модели входных нейронов этой категории связаны между входным стимулом, который может быть фармакологическим или естественным, и вероятность всплеска. Входящие каскад этих моделей не является электрическим, имеет либо фармакологические (химические) единицы, которые имеют другие физические единицы, которые имеют другие физические силы, такие как свет, звук формы физического давления. Кроме того, выходной каскад представляет вероятность возникновения всплеска, а не электрического напряжения.

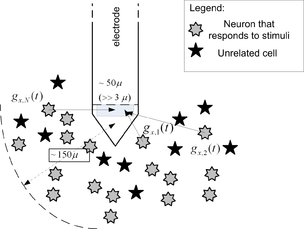Рис. 3. Внеклеточные измерения: улавливает всплески с более низкой амплитудой, часто от нескольких источников выбросов, в результате чего происходит его близость к источникам. Несмотря на увеличенные уровни амплитуды, создаваемые этим методом, он также имеет несколько преимуществ: 1) легче получить экспериментально; 2) Надежен и служит дольше; 3) Может отражать доминирующий эффект, особенно когда проводится в анатомической области со многими похожими клетками.

Хотя в науке и технике нет ничего необычного в наличии нескольких описательных моделей для разных уровней абстракции / детализации, различных, иногда противоречие, биологических моделей нейронов исключительно высоки. Это частично является результатом различных различных экспериментальных ситуаций и сложных ситуаций одного и того же взаимодействия различных клеток (сетевые эффекты). Чтобы ускорить переход к единой теории, мы перечисляем несколько моделей в каждой категории и, где это возможно, также ссылки на поддерживающие эксперименты.

Содержание

Электрический ввод –Модели выходного мембранного напряжения

этой

Модели в категории описывают взаимосвязь между мембранными токами нейронов на входном каскаде и мембранным напряжением на выходном каскаде. Наиболее широкое экспериментальное исследование этой категории было проведено Ходжкином-Хаксли в начале 1950-х годов с использованием экспериментальной установки, которая прокалывала клеточную мембрану и позволяет вызвать определенное напряжение / ток мембраны.

Самые современные электрические нейронные интерфейсы применяют внеклеточную электрическую стимуляцию, чтобы избежать прокола мембраны, что может привести к гибели клеток и повреждению тканей. Следовательно, неясно, в какой мощности электрические модели нейронов подходят для внеклеточной стимуляции (см., Например).

Ходжкина - Хаксли

Экспериментальные данные, подтверждающие модель
Свойство модели HH	Ссылки
Форма отдельного пика
Идентичность участвующих других
Пиковая скорость по аксону

Модель Ходжкина - Хаксли (модель HH) - это взаимосвязь между потоком ионных токов через мембрану нейрональной клетки и мембранным напряжением клетки. Он состоит из набора нелинейных дифференциальных уравнений, описывающих поведение ионных каналов, пронизывающих клеточную мембрану гигантского аксона кальмара. За эту работу Ходжкин и Хаксли были удостоены Нобелевской премии 1963 года по физиологии и медицине.

Мы отмечаем взаимосвязь напряжение-ток с множественными зависимыми от напряжения токами, заряжающими клеточную мембрану емкостью C m

C md V (t) dt = - ∑ i I i (t, V) {\ displaystyle C _ {\ mathrm {m}} {\ frac {dV (t)} {dt}} = - \ sum _ {i} I_ {i} (t, V)}

C _ {{\ mathrm {m}}} {\ гидроразрыв {dV (t)} {dt}} = - \ sum _ {i} I_ {i} (t, V)

Приведенное выше уравнение - это время производная закона емкости, Q = CV, где изменение общего заряда должно быть объяснено как сумма по токам. Каждый ток задается законом Ома как

I (t, V) = g (t, V) ⋅ (V - V eq) {\ displaystyle I (t, V) = g (t, V) \ cdot (VV _ {\ mathrm {eq}})}

I (t, V) знак равно g (t, V) \ cdot (VV _ {\ mathrm {eq}}})

где g (t, V) - это проводимость, или обратное сопротивление, которое можно разложить на постоянное среднее значение ḡ и совместную активацию и инактивации m и h, которые определяют, сколько может проходить через доступные мембранные каналы. Это расширение задается формулой

g (t, V) = g ¯ ⋅ m (t, V) p ⋅ h (t, V) q {\ displaystyle g (t, V) = {\ bar {g}} \ cdot m (t, V) ^ {p} \ cdot h (t, V) ^ {q}}

g (t, V) = {\ bar {g}} \ cdot m ( t, V) ^ {p} \ cdot h (t, V) ^ {q}

и наши дроби следуют кинетике первого порядка

dm (t, V) dt = m ∞ (В) - м (т, В) τ м (В) знак равно α м (В) ⋅ (1 - м) - β м (В) ⋅ м {\ Displaystyle {\ гидроразрыва {дм (т, V)} {dt} } = {\ frac {m _ {\ infty} (V) -m (t, V)} {\ tau _ {\ mathrm {m}} (V)}} = \ alpha _ {\ mathrm {m}} (V) \ cdot (1-m) - \ beta _ {\ mathrm {m}} (V) \ cdot m}

{\ frac {dm (t, V)} {dt}} = {\ frac {m _ {\ infty} (V) -m (t, V)} {\ tau _ {{\ mathrm {m}}} (V)}} = \ alpha _ {{\ mathrm {m}}} (V) \ cdot ( 1-м) - \ beta _ {{\ mathrm {m}}} (V) \ cdot m

с аналогичной динамикой для h, где мы можем использовать либо τ, либо m ∞ или α и β, чтобы определить наши доли ворот.

Модель Ходжкина - Хаксли может быть расширена за счет включения дополнительных ионных токов. Обычно они включают входящие токи Ca и Na, а также несколько разновидностей выходных токов K, включая ток утечки.

Конечным результатом может быть около 20 параметров, которые необходимо оценить или измерить для получения точной модели. Для сложных систем нейронов интеграция соотношений требует больших вычислительных ресурсов. Поэтому необходимы тщательные упрощения модели Ходжкина - Хаксли.

Идеальная интеграция и запуск

Одна из самых ранних моделей нейрона - это идеальная модель интеграции и запуска, впервые исследованная в 1907 году Луи Лапик. Нейрон его представлен мембранным напряжением V, который вовлекается во время стимуляции входным током I (t) согласно

I (t) = C d V (t) dt {\ displaystyle I (t) = C {\ frac {dV (t)} {dt}}}

{\ displaystyle I (t) = C {\ frac {dV (t)} {dt}}}

, который является просто временной производной законом емкости, Q = CV. Когда подается входной ток, мембранное напряжение увеличивается со временем, пока не достигнет постоянного порогового значения V th, в этот момент возникает всплеск дельта-функции, и напряжение сбрасывается до состояния покоя. потенциал, после чего модель продолжает работать. Таким образом, частота срабатывания модели неограниченно линейно увеличенный класс входного тока.

Модель можно сделать более точной, введя рефрактерный период t ref, который ограничивает частоту срабатывания нейрона, предотвращая его срабатывание в течение этого периода. Для постоянного входа I (t) = I пороговое напряжение достигается по истечении времени интегрирования t int = CV thr / I после старта с нуля. После сброса рефрактерный период вводит мертвое время, так что общее время до следующего срабатывания равно t ref + t int. Частота срабатывания обратна полному интервалу между импульсами (включая мертвое время). Таким образом, частота срабатывания как функция постоянного входного тока равна

f (I) = ICV th + tref I {\ displaystyle \, \! F (I) = {\ frac {I} {C _ {\ mathrm {}} V _ {\ mathrm {th}} + t _ {\ mathrm {ref}} I}}}

{\ displaystyle \, \! f (I) = {\ frac {I} {C _ {\ mathrm {}} V_ {\ mathrm {th}} + t _ {\ mathrm {ref}} I}}}

Недостатком этой модели является то, что она не входит ни адаптации, ни утечки. Заработок в области ускорения. Эта характеристика явно не соответствует наблюдаемому поведению нейронов. Следующие расширения делают модель интеграции и стрельбы более правдоподобной биологической точки зрения.

Негерметичная интеграция и возгорание

Модель протекающей интеграции и возгорания, восходящая к Луи Лапику, по сравнению с негерметичной интеграцией, содержит смоделировать член "утечки" в уравнении мембранный, отражающий диффузию через мембрану. Уравнение модели выглядит так (модель с утечкой интегрирования и возгорания, глава 4,1 дюйма)

C md V m (t) dt = I (t) - V m (t) R m {\ displaystyle С _ {\ mathrm {m}} {\ frac {dV _ {\ mathrm {m}} (t)} {dt}} = I (t) - {\ frac {V _ {\ mathrm {m}} (t)} {R _ {\ mathrm {m}}}}}

{\ displaystyle C _ { \ mathrm {m}} {\ frac {dV _ {\ mathrm {m}} (t)} {dt}} = I (t) - {\ frac {V _ {\ mathrm {m}} (t)} {R _ {\ mathrm {m}}}}}

где V m - напряжение на клеточной мембране, а R m - сопротивление мембраны. (Модель интегрирования и возгорания без утечки восстанавливается в пределе R m до бесконечности, т.е. если мембрана является идеальным изолятором). Уравнение модели действительно для произвольного зависящего от времени входа, пока не достигнуто пороговое значение V th ; после этого мембранный потенциал сбрасывается.

Для постоянного входа минимальный вход для достижения равенства I th = V th / R m. Предполагаемая сброс на ноль, частота срабатывания выглядит как

f (I) = {0, I ≤ I th [tref - R m C m log ⁡ (1 - V th IR m)] - 1, I>I th { \ displaystyle f (I) = {\ begin {case} 0, I \ leq I _ {\ mathrm {th}} \\ {[} t _ {\ mathrm {ref}} -R _ {\ mathrm {m }} C _ {\ mathrm {m}} \ log (1 - {\ tfrac {V _ {\ mathrm {th}}} {IR _ {\ mathrm {m}}}}) {]} ^ {- 1 }, I>I _ {\ mathrm {th}} \ end {ases}}

$f(I)={\begin{cases}0,I\leq I_{{\mathrm {th}}}\\{[}t_{{\mathrm {ref}}}-R_{{\mathrm {m}}}C_{{\mathrm {m}}}\log(1-{\tfrac {V_{{\mathrm {th}}}}{IR_{{\mathrm {m}}}}}){]}^{{-1}},I>I _ {\ mathrm {th}}} \ end {ases}}$

который сходится для больших входных токов к предыдущей модели безрактерчек с периодом. также может быть распространено на тормозящие нейроны.

Самый большой недостаток Дырявого нейрона интеграции и запуска заключается в том, что он не содержит нейронной адаптации, поэтому он может описать экспериментально измеренную последовательность импульсов в ответ на постоянный входной то к. Этот недостаток устранен в обобщенной версии "Интегрируй и стреляй". модели, которые также вводят переменную адаптацию с высокой степенью точности предсказывать время спайков корковых нейронов при токе.

Адаптивная интеграция и запуск

Нейрональная адаптация относится к Дело в том, что даже при наличии постоянной подачи тока в некоторые интервалы между выбросами на выходе увеличиваются. Адаптивная модель нейрона интеграции и активации сочетает интеграцию напряжения V с одними или адаптационными переменными w k (см. главу 6.1 в учебнике Neuronal Динамика)

$τ мд В м (т) dt знак равно RI (т) - [В м (т) - Е м] - R ∑ kwk {\ displaystyle \ tau _ {\ mathrm {m}} {\ frac {dV _ {\ mathrm {m}} (t)} {dt}} = RI (t) - [V _ {\ mathrm {m}} (t) -E _ {\ mathrm {m}}] - R \ sum _ {k} w_ {k}}$ ${\ displaystyle \ tau _ {\ mathrm {m}} {\ frac {dV _ {\ mathrm {m}} (t)} {dt} } = RI (t) - [V _ {\ mathrm {m}} (t) -E _ {\ mathrm {m}}] - R \ sum _ {k} w_ {k}}$

$τ kdwk (t) dt = - ak [V m (t) - E m] - wk + bk τ k ∑ е δ (t - tf) {\ displaystyle \ tau _ {k} {\ frac {dw_ {k} (t)} {dt}} = - a_ {k} [V _ {\ mathrm {m}} (t) -E _ {\ mathrm {m}}] - w_ {k } + b_ {k} \ tau _ {k} \ sum _ {f} \ delta (tt ^ {f})}$ ${\ d isplaystyle \ tau _ {k} {\ frac {dw_ {k} (t)} {dt}} = - a_ {k} [V_ {\ mathrm {m}} (t) -E _ {\ mathrm {m} }] - w_ {k} + b_ {k} \ tau _ {k} \ sum _ {f} \ delta (tt ^ {f})}$

где $τ m {\ displaystyle \ tau _ {m}}$ $\ tau _ {m}$ - постоянная времени мембраны, w k - текущий номер адаптации с индексом k, $τ k {\ displaystyle \ tau _ {k}}$ $\ tau _ {k}$ - это постоянная времени адаптационного тока w k, E m - потенциал покоя, t - время срабатывания нейрон а, а греческая дельта обозначает Di Дельта-функция rac. Когда напряжение начинается порога срабатывания, напряжение сбрасывается до значения V r ниже порога срабатывания. Значение сброса - один из важных параметров модели. Простейшая модель адаптации имеет только одну переменную адаптацию w, сумма по k удаляется.

Интегрируйте и запускайте нейроны с одной или несколькими переменными адаптациями, которые включают множество возбудителей нейронов в ответ на постоянную стимуляцию, включая адаптацию, взрыв и начальный взрыв. Более того, адаптивные нейроны с интеграцией и запуском с использованием адаптационных переменными предсказывать время всплесков корковых нейронов при зависящей от времени инъекции тока в сому.

Неплотный интегрируй-и-стреляй дробного порядка

Недавние достижения в области вычислительного и теоретического дробного исчисления привели к новой форме модели, получившей название «интегрировать и запустить с утечкой дробного порядка». «Преимущество этой модели» состоит в том, что она может использовать эффекты адаптации с помощью одной новой модели. Модель имеет следующий вид

I (t) - V m (t) R m = C md α V m (t) d α t {\ displaystyle I (t) - {\ frac {V _ {\ mathrm {m }} (t)} {R _ {\ mathrm {m}}}} = C _ {\ mathrm {m}} {\ frac {d ^ {\ alpha} V _ {\ mathrm {m}} (t) } {d ^ {\ alpha} t}}}

{\ displaystyle I (t) - {\ frac {V _ {\ mathrm {m}} (t)} {R _ {\ mathrm {m}}}} = C _ {\ mathrm {m}} {\ frac {d ^ {\ alpha} V _ {\ mathrm {m}} (t)} {d ^ {\ alpha} t}}}

Как только напряжение достигает порогового значения, оно сбрасывается. Для учета адаптации нейронов в экспериментальных данных использовалась дробная интеграция.

«Экспоненциальная интеграция и запуск» и «Адаптивная экспоненциальная интеграция и запуск»

В экспоненциальной интегрировать и активировать модель, генерация всплесков экспоненциальна в соответствии с уравнением:

d В dt - р τ м я (t) знак равно 1 τ м [Е м - V + Δ T ехр ⁡ (V - VT Δ T)] {\ displaystyle {\ frac {dV} {dt}} - {\ frac {R} {\ tau _ {m}}} I (t) = {\ frac {1} {\ tau _ {m}}} [E_ {m} -V + \ Delta _ {T} \ exp \ left ({\ frac {V-V_ {T}} {\ Delta _ {T}}} \ right)]}

{\ displaystyle {\ frac {dV} {dt}} - {\ frac {R} {\ tau _ {m}}} I (t) = {\ frac {1} {\ tau _ {m}}} [E_ {m} -V + \ Delta _ {T} \ exp \ left ({\ frac {V-V_ {T}} {\ Delta _ {T}}} \ right)]}

где $V {\ displaystyle V}$ $V$ - мембранный потенциал, $VT {\ displaystyle V_ {T}}$ $V_ {T}$ - порог внутреннего мембранного времени, $τ m {\ displaystyle \ tau _ {m}}$ $\ tau _ {m}$ - постоянная мембрана, $E m {\ displaystyle E_ {m}}$ $E_ {m}$ - потенциал покоя, а $Δ T {\ displaystyle \ Delta _ {T}}$ $\ Delta_T$ - резкость инициации потенциала действия, обычно около 1 мВ для кортикальных пирамидных нейронов. Как только мембранный потенциал пересекает $V T {\ displaystyle V_ {T}}$ $V_ {T}$ , он расходуется до бесконечности за конечное время. При численном моделировании интегрирование останавливается, если мембранный потенциал достигает произвольного порога (намного большего, чем $VT {\ displaystyle V_ {T}}$ $V_ {T}$ ), при котором мембранный потенциал сбрасывается до значения V г. Значение сброса напряжения V r является одним из важных параметров модели. Важно отметить, что правая часть приведенного выше уравнения содержит нелинейность, которую можно напрямую извлечь из экспериментальных данных. В этом смысле экспоненциальная нелинейность убедительно подтверждается экспериментальными данными.

В адаптивном экспоненциальном нейроне интегрирования и включения указанная выше экспоненциальная нелинейность уравнения напряжения комбинируется с переменной адаптации w

$τ md V dt = RI (t) + [E m - V + Δ T exp ⁡ (V - VT Δ T)] - R w {\ displaystyle \ tau _ {m} {\ frac {dV} {dt}} = RI (t) + [E_ {m } -V + \ Delta _ {T} \ exp \ left ({\ frac {V-V_ {T}} {\ Delta _ {T}}} \ right)] - Rw}$ ${\ displaystyle \ tau _ {m} {\ frac {dV} {dt}} = RI ( t) + [E_ {m} -V + \ Delta _ {T} \ exp \ left ({\ frac {V-V_ {T}} {\ Delta _ {T}})} \ right)] - Rw}$

$τ dw (t) dt Знак равно - a [В м (T) - E м] - вес + б τ δ (t - tf) {\ displaystyle \ tau {\ frac {dw (t)} {dt}} = - a [V _ {\ mathrm {m}} (t) -E _ {\ mathrm {m}}] - w + b \ tau \ delta (tt ^ {f})}$ ${\ displaystyle \ tau {\ frac {dw (t)} {dt}} = - a [V _ {\ mathrm {m}} (t) -E _ {\ mathrm {m}}] - w + b \ tau \ delta (tt ^ {f})}$

где w обозначает ток адаптации во времени масштаб $τ {\ displaystyle \ tau}$ $\ tau$ . Важными параметрами модели являются значение сброса напряжения V r, внутренний порог $VT {\ displaystyle V_ {T}}$ $V_ {T}$ , постоянные времени $τ {\ displaystyle \ tau}$ $\ tau$ и $τ m {\ displaystyle \ tau _ {m}}$ $\ tau _ {m}$ , а также параметры связи a и b. Адаптивная экспоненциальная модель интегрирования и зажигания наследует экспериментально полученную нелинейность напряжения экспоненциальной модели интегрирования и зажигания. Но, выходя за рамки этой модели, он также может объяснить различные паттерны нейронального возбуждения в ответ на постоянную стимуляцию, включая адаптацию, взрыв и начальный взрыв.

Гальвес-Лёчербах

3D-визуализация Гальвеса-Лёчербаха модель для биологических нейронных сетей. Эта визуализация настроена для 4000 нейронов (4 слоя с однойпопуляцией тормозных нейронов и одной популяцией возбуждающих нейронов в каждом) через 180 интервалов времени.

Модель Гальвса - Лёчербаха представляет собой конкретное развитие дырявая модель интеграции и возгорания. Это по своей сути стохастический. Его разработали математики Антонио Гальвес и. С учетом указанной модели, вероятность того, что данный нейрон $i {\ displaystyle i}$ $i$ всплескивает за период времени $t {\ displaystyle t}$ $t$ , может быть описана как

$P rob ⁡ (X t (i) = 1 | F t - 1) = ϕ i (∑ j ∈ IW j → i ∑ s = L tit - 1 gj (t - s) X s (j), τ - L ti), {\ displaystyle \ mathop {\ mathrm {Prob}} (X_ {t} (i) = 1 | {\ mathcal {F}} _ {t-1}) = \ phi _ {i} { \ Biggl (} \ sum _ {j \ in I} W_ {j \ rightarrow i} \ sum _ {s = L_ {t} ^ {i}} ^ {t-1} g_ {j} (ts) X_ { s} (j), ~~~ t-L_ {t} ^ {i} {\ Biggl)},}$ ${\ displaystyle \ mathop {\ mathrm {Prob}} (X_ {t} (i) = 1 | {\ mathcal {F}} _ {t-1}) = \ phi _ {i} {\ Biggl (} \ sum _ {j \ in I} W_ {j \ rightarrow i} \ sum _ {s = L_ { t} ^ {i}} ^ {t-1} g_ {j} (ts) X_ {s} (j), ~~~ t-L_ {t} ^ {i} {\ Biggl)},}$

где $W j → i {\ displaystyle W_ {j \ rightarrow i}}$ ${\ displaystyle W_ {j \ rightarrow i}}$ - синаптический вес, описывающий влияние нейрона $j {\ displaystyle j}$ $j$ на нейрон $i {\ displaystyle i}$ $i$ , $gj {\ displaystyle g_ {j}}$ $g_ {j}$ выражает утечку, а $L ti {\ displaystyle L_ {t} ^ {i}}$ ${\ displaystyle L_ {t} ^ {i}}$ предоставляет историю всплесков нейрона $я {\ displaystyle i }$ $i$ до $t {\ displaystyle t}$ $t$ , согласно

$L ti = sup {s < t : X s ( i) = 1 }. {\displaystyle L_{t}^{i}={\text{sup}}\{s$ ${\ displaystyle L_ {t} ^ {i} = {\ text {sup}} \ {s <t: X_ {s } (i) = 1 \}.}$

ФитцХью - Нагумо

Шве Упрощения эпинга для Ходжкина-Хаксли были введены ФитцХью и Нагумо в 1961 и 1962 годах. Стремясь описать «регенеративное самовозбуждение» с помощью нелинейного мембранного напряжения с положительной обратной связью и восстановления с помощью линейного напряжения затвора с отрицательной обратной связью, они разработали описанную модель на

d V dt = V - V 3/3 - w + I ext τ dwdt = V - a - bw {\ displaystyle {\ begin {array} {rcl} {\ dfrac {dV} {dt}} = VV ^ {3} / 3-w + I _ {\ mathrm {ext }} \\\ tau {\ dfrac {dw} {dt}} = Va-bw \ end {array}}

{\ displaystyle {\ begin {array} {rcl} {\ dfrac {dV} {dt}} = V -V ^ {3} / 3- w + I _ {\ mathrm {ext}} \\\ tau {\ dfrac {dw} {dt}} = Va-bw \ end {array}}}

, где мы снова имеем мембранное напряжение и входной ток с более медленным общим напряжением затвора w и экспериментально определенными значениями a = -0,7, b = 0,8, τ = 1 / 0,08. Эта модель явно не выводится из биологии. Экспериментальная поддержка слабая.

Моррис-Лекар

В 1981 году Моррис и Лекар объединили модели Ходжкина-Хаксли и ФитцХью-Нагумо в модели потенциалаозависимого кальциевого канала с калиевым каналом с задержанным выпрямителем, представленным

C d V dt Знак равно - I ion (V, w) + I dwdt = ϕ ⋅ вес ∞ - вес τ w {\ displaystyle {\ begin {array} {rcl} C {\ dfrac {dV} {dt}} = - I _ {\ mathrm {ion}} (V, w) + I \\ {\ dfrac {dw} {dt}} = \ phi \ cdot {\ dfrac {w _ {\ infty} -w} {\ tau _ {w}}} \ end {array}}}

{\ displaystyle {\ begin {array} {rcl} C {\ dfrac {dV} {dt}} = - I _ {\ mathrm {ion}} (V, w) + I \\ {\ dfrac {dw} {dt}} = \ ph i \ cdot {\ dfrac {w _ {\ infty} - w} {\ tau _ {w}}} \ end {array}}

где $I ion (V, w) = g ¯ C am ∞ ⋅ (V - VC a) + g ¯ K w ⋅ (V - VK) + г ¯ L ⋅ (V - VL) {\ displaystyle I _ {\ mathrm {ion}} (V, w) = {\ bar {g}} _ {\ mathrm {Ca}} m _ {\ infty} \ cdot (VV _ {\ mathrm {Ca}}) + {\ bar {g}} _ {\ mathrm {K}} w \ cdot (VV _ {\ mathrm {K}}) + {\ bar {g}} _ {\ mathrm {L}} \ cdot (VV _ {\ mathrm {L}})}$ $I _ {{\ mathrm {ion} }} (V, w) = {\ bar {g}} _ {{\ mathrm {Ca}}} m _ {{\ infty}} \ cdot (VV _ {{\ mathrm {Ca}}}) + { \ bar {g}} _ {{\ mathrm {K}}} w \ cdot (VV _ {{\ mathrm {K}}}) + {\ bar {g}} _ {{\ mathrm {L}}} \ cdot (VV _ {{\ mathrm {L}}})$ .

Хиндмарш - Роуз

Основываясь на модели ФитцХью - Нагумо, Хиндмарш и Роузили в 1984 году модель нейронной активности описывалась тремя связанными дифференциа льными уравнениями первого порядка:

dxdt = y + 3 x 2 - x 3 - z + I dydt = 1–5 x 2 - ydzdt = r ⋅ (4 (x + 8 5) - z) {\ displaystyle {\ begin {array} {rcl} {\ dfrac {dx} {dt}} = y + 3x ^ {2} -x ^ {3} -z + I \\ {\ dfrac {dy} {dt}} = 1-5x ^ {2} -y \\ {\ dfrac {dz} {dt}} = r \ cdot (4 (x + {\ tfrac {8} {5}}) - z) \ end {array}}}

{\ displaystyle {\ begin {массив } {rcl} {\ dfrac {dx} {dt}} = y + 3x ^ {2} -x ^ {3} -z + I \\ {\ dfrac {dy} {dt}} = 1 -5x ^ {2} -y \\ {\ dfrac {dz} {dt}} = r \ cdot (4 (x + {\ tfrac {8} {5}}) - z) \ end {массив} }}

с r = x + y + z и r ≈ 10, так что переменная z только меняется очень медленно. Эта дополнительная математическая допускает большое разнообразие динамических характеристик мембранного, описываемого типа x модели, включая хаотическую динамику. Это делает модель нейрона Хиндмарша - Роуза очень полезной, поскольку качественно все еще простой, позволяет описать множество различных паттернов действия, наблюдаемых в экспериментах.

Тета-модель и квадратичная интеграция-и-огонь.

тета-модель, или каноническая модель Эрментроута - Копелла, математически эквивалентна квадратичной модели интегрирования и включения, которая, в свою очередь, является приближением к экспоненциальной модель интеграции и стрельбы и модель Ходжкина-Хаксли. Это называется канонической моделью, потому что это одна из общих моделей для постоянного входа, близкого к точке бифуркации, что означает близость перехода от бесшумного к повторяющемуся срабатыванию.

Уравнение для квадратичного интегрирования-и- Модель пожара (см. главу 5.3 в учебнике «Нейронная динамика»)

$τ md V m (t) dt = (I - I 0) R + [В м (т) - Е м] [В м (т) - VT] {\ displaystyle \ tau _ {\ mathrm {m}} {\ frac {dV _ {\ mathrm {m}} (т)} {dt}} = (I-I_ {0}) R + [V _ {\ mathrm {m}} (t) -E _ {\ mathrm {m}}] [V _ {\ mathrm {m} } (t) -V _ {\ mathrm {T}}]}$ ${\ displaystyle \ tau _ {\ mathrm {m}} {\ frac {dV _ {\ mathrm {m}} (t)} {dt}} = (I-I_ {0}) R + [V _ {\ mathrm {m }} (т) -E _ {\ mathrm {m}}] [V _ {\ mathrm {m}} (t) -V _ {\ mathrm {T}}]}$

Эквивалентность тета-модели и квадратичной интеграции-и-зажигания, например, рассматривается в главе 4.1.2.2 Spiking Neuron Models.

Для входа I (t), который изменен со временем или вдали от точки бифуркации, предпочтительнее работать с экспоненциальной моделью интегрировать и запустить (если кто-то хочет остаться в классе одномерных моделей нейронов), потому что реальные нейроны демонстрируют нелинейность эксцентриситета. Поненциальная модель интегрирования и возгорания.

Теория кабеля

Теория кабеля дендритную ветвь как цилиндрическую стойкую, подвергающуюся регулярному шаблону бифуркации, как ветви на дереве. Для одного цилиндра или всего дерева входная проводимость в основании (где дерево встречается с телом ячейками или любой такой границей) как определяется как

G in = G ∞ tanh ⁡ (L) + GL 1 + (GL / G ∞) tanh ⁡ ( L) {\ displaystyle G_ {in} = {\ frac {G _ {\ infty} \ tanh (L) + G_ {L}} {1+ (G_ {L} / G _ {\ infty}) \ tanh ( L)}}}

G _ {{in}} = {\ frac {G_ {\ infty} \ tanh (L) + G_ {L }} {1+ (G_ {L} / G _ {\ infty}) \ tanh (L)}}

где L - электротоническая длина цилиндра, которая зависит от его длины, диаметра и сопротивления. Простой рекурсивный алгоритм линейно переводится с ветвей и другая программа для эффективной проводимости дерева. Это задается как

GD = G m AD tanh ⁡ (LD) / LD {\ displaystyle \, \! G_ {D} = G_ {m} A_ {D} \ tanh (L_ {D}) / L_ {D}}

\, \! G_ {D} = G_ {m} A_ {D} \ tanh (L_ {D}) / L_ {D}

где A D = πld - общая площадь поверхности дерева общей длиной l, а L D - его полная электротонная длина. Для всегорона, в котором проводимость нейрона клетки составляет G S, проводимость мембраны на единицу площади равна G md = G m / A, мы на общую проводимость нейрона G N для n дендритных деревьев путем сложения проводимости всех деревьев и сомы, полученной как

GN = GS + ∑ j = 1 n AD j F dgaj {\ displaystyle G_ {N} = G_ {S } + \ sum _ {j = 1} ^ {n} A_ {D_ {j}} F_ {dga_ {j}}}

G_ {N} = G_ {S} + \ sum _ {{j = 1}} ^ {n} A _ {{D_ {j}}} F _ {{dga_ {j}}}

где мы можем найти общий поправочный коэффициент F dga экспериментально, отмечая G D = G mdADFdga.

Компартментные модели

Модель кабеля делает ряд упрощений для получения закрытых аналитических результатов, а именно, что дендритная ветвь должна разветвляться в убывающих парах по фиксированной схеме. Компартментная модель допускает любую желаемую топологию с произвольными ветвями и длинами, но упрощает взаимодействие между ветвями для компенсации. Таким образом, две модели дают дополнительные результаты.

Каждая отдельная часть или дендрита моделируется прямым цилиндром произвольной длины l и диаметром d, который соединяется с фиксированным сопротивлением с любым разветвленным цилиндров. Определим коэффициент проводимости i-го цилиндра как B i = G i / G ∞, где $G ∞ = π d 3/2 2 Р я р м {\ displaystyle G _ {\ infty} = {\ tfrac {\ pi d ^ {3/2}} {2 {\ sqrt {R_ {i} R_ {m}}}}}}$ $G _ {\ infty} = {\ tfrac {\ pi d ^ { {3/2}}} {2 {\ sqrt {R_ {i} R_ {m}}}}}$ и R i - сопротивление между текущим отсеком и следующим. Мы получаем серию коэффициентов проводимости внутри и вне отсека, внося поправки в нормальную динамику B out, i = B in, i + 1, как

$B out, я знак равно B in, я + 1 (di + 1 / di) 3/2 R m, i + 1 / R m, i {\ displaystyle B _ {\ mathrm {out}, i} = {\ frac {B _ { \ mathrm {in}, i + 1} (d_ {i + 1} / d_ {i}) ^ {3/2}} {\ sqrt {R _ {\ mathrm {m}, i + 1} / R_ { \ mathrm {m}, i}}}}}$ $B _ {{{\ mathrm {out}}, i}} = {\ frac {B _ {{{\ mathrm {in}}, i + 1}} (d _ {{i + 1}} / d_ { i}) ^ {{3/2}}} {{\ sqrt {R _ {{{\ mathrm {m}}, i + 1}} / R _ {{{\ mathrm {m}}, i}} }}}}$
$B in, i = B out, i + tanh ⁡ X i 1 + B out, я tanh ⁡ X i {\ displaystyle B _ {\ mathrm {in}, i} = {\ frac {B _ {\ mathrm {out}, i} + \ tanh X_ {i}} {1 + B _ {\ mathrm {out}, i} \ tanh X_ {i}}}}$ $B _ {{{\ mathrm {in}}, i}} = {\ frac {B _ {{{\ mathrm {out}}, i}} + \ tanh X_ {i}} { 1 + B _ {{{\ mathrm {out}}, i}} \ tanh X_ {i}}}$
$B out, par = B in, dau 1 (ddau 1 / dpar) 3/2 R m, dau 1 / R m, par + B in, dau 2 (ddau 2 / dpar) 3/2 R m, dau 2 / R m, par +… {\ displaystyle B _ {\ mathrm {out, par}} = {\ frac {B _ {\ mathrm {in, dau1}} (d _ {\ mathrm {dau1}} / d _ {\ mathrm {par}}) ^ {3/2}} {\ sqrt {R _ {\ mathrm {m, dau1}} / R _ {\ mathrm {m, par}}}}} + {\ гидроразрыв {B _ {\ mathrm {in, dau2}} (d _ {\ mathrm {dau 2}} / d _ {\ mathrm {par}}) ^ {3/2}} {\ sqrt {R _ {\ mathrm {m, dau2}} / R _ {\ mathrm {m, par}}}} } + \ ldots}$ $B _ {{\ mathrm {out, par}}} = {\ frac {B _ { {\ mathrm {in, dau1}}} (d_ {{\ mathrm {dau1}}} / d _ {{\ mathrm {par}}}) ^ {{3/2}}} {{\ sqrt {R _ {{\ mathrm {m, dau1}}} / R _ {{\ mathrm {m, par}}}}}}} + {\ frac {B _ {{\ mathrm {in, dau2}}} (d _ {{\ mathrm {dau2} }}} / d _ {{\ mathrm {par})}}) ^ {{3/2}}} {{\ sqrt {R _ {\ mathrm {m, dau2}}} / R _ {{\ mathrm {m, par}}}}}}} + \ ldots$

где последнее уравнение относится к родителям и дочерям в филиалах, а $X i = li 4 R idi R m {\ displaystyle X_ {i} = {\ tfrac {l_ {i} {\ sqrt {4R_ {i}}}}} {\ sqrt {d_ {i} R_ {m}}}}}$ $X_ {i} = {\ tfrac {l_ {i} {\ sqrt {4R_ {i}}}} {{\ sqrt {d_) {i} R_ {m}}}}$ . Мы можем повторить эти уравнения по дереву до тех пор, пока не получим точку, в которой дендриты соединяются с телом клетки (сомой), где коэффициент проводимости равен B дюйм, стержень. Тогда наша общая проводимость нейронов определяется как

GN = A soma R m, soma + ∑ j B in, stem, j G ∞, j {\ displaystyle G_ {N} = {\ frac {A _ {\ mathrm {soma }}} {R _ {\ mathrm {m, soma}}}} + \ sum _ {j} B _ {\ mathrm {in, stem}, j} G _ {\ infty, j}}

G_ {N} = {\ frac {A _ {{\ mathrm {soma}}}} {R _ {{\ mathrm {m, soma}}}}} + \ sum _ {j} B_ {{ {\ mathrm {in, stem}}, j}} G _ {{\ infty, j}}

Пример Компартментную модель нейрона с алгоритмом уменьшения количества отсеков (увеличения скорости вычислений) и при этом основных показателей можно найти в.

Модели нейронов естественного входного стимула

Модели этой категории были созданы в результате экспериментов с естественной стимуляцией, такие как свет, звук, прикосновение или запах. В этих условиях экспериментов характер спайков, стимулирует результаты испытаний к испытанию, но усредненный ответ от нескольких испытаний часто сходится к четкому образцу. Следовательно, модели этой категории генерируют вероятностную взаимосвязь между входным стимулом и возникновением всплесков.

Неоднородная модель пуассоновского процесса (Зиберт)

Зиберт смоделировалтерн возбуждения спайков нейрона, используя не- однородную модель пуассоновского процесса, следующие эксперименты со слуховой система. Согласно Зиберту, вероятность всплеска в интервале времени $[t, t + Δ t] {\ displaystyle [t, t + \ Delta _ {t}]}$ ${\ displaystyle [t, t + \ Delta _ {t}]}$ пропорциональна неотрицательная функция $г [s (t)] {\ displaystyle g [s (t)]}$ ${\ displaystyle g [s (t)]}$ , где $s (t) {\ displaystyle s (t)}$ $s(t)$ - необработанный стимул:

$П спайк (t ∈ [t ′, t ′ + Δ t]) = Δ t ⋅ g [s (t)] {\ displaystyle P_ {spike} (t \ in [t ', t' + \ Delta _ { t}]) = \ Delta _ {t} \ cdot g [s (t)]}$ $P_{spike}(t\in [t',t'+\Delta _{t}])=\Delta _{t}\cdot g[s(t)]$

Сиберт рассматривал несколько функций как $g [s (t)] {\ displaystyle g [s (t)]}$ ${\ displaystyle g [s (t)]}$ , включая $g [s (t)] ∝ s 2 (t) {\ displaystyle g [s (t)] \ propto s ^ {2} (t)}$ ${\ displaystyle г [s (t)] \ propto s ^ {2} (t)}$ для низкой мощности стимула.

Основное преимущество модели Зиберта - ее простота. Недостатком модели является ее неспособность должным образом отразить следующие явления:

свойство нейрона подчеркивать края в ответ на импульс стимула.
насыщение скорости возбуждения.
Значения межпикового интервала- гистограммы при значениях коротких интервалов (близких к нулю).

Эти недостатки устранены моделью Маркова с двумя состояниями.

Два состояния Модель Маркова (Носсенсон и Мессер)

Модель пикового нейрона, разработанная Носсенсоном и Мессером, вырабатывает вероятность того, что нейрон вызовет спайк в зависимости от внешнего или фармакологического стимула. Модель состоит из каскада модели рецепторного слоя и модели нейрона с импульсами, как показано на рис. 4. Связь между внешним стимулом и вероятностью выброса осуществляется в два этапа: во-первых, модель рецепторной клетки преобразует исходный внешний стимул. с концентрацией нейротрансмиттера, то модель пикового нейрона связывает концентрацию нейротрансмиттера с частотой срабатывания (вероятность пика). Таким образом, модель импульсного нейрона сама по себе зависит от концентрации нейротрансмиттера на входной стадии.

Рис. 4: Блок-схема высокого уровня рецепторного слоя и модель нейрона, разработанная Носсенсоном и Мессером.

Рис. 5. Прогноз для срабатывания. частота в ответ на импульсный стимул в соответствии с моделью Носсенсона и Мессера.

Важной особенностью этой модели является прогнозирование модели частоты срабатывания нейронов, которая фиксирует, используя небольшое количество свободных параметров, характерную реакцию с подчеркнутым краем нейронов к импульсу стимула, как показано на рис. 5. Скорость возбуждения определяется как нормализованная вероятность возбуждения нервного импульса, так и величина, пропорциональная току нейротрансмиттеров, высвобождаемых клеткой. Выражение для скорости стрельбы имеет следующий вид:

$R fire (t) = P spike (t; Δ t) Δ t = [y (t) + R 0] ⋅ P 0 (t) {\ displaystyle R_ {огонь} (t) = {\ frac {P_ {spike} (t; \ Delta _ {t})} {\ Delta _ {t}}} = [y (t) + R_ {0}] \ cdot P_ {0} (t)}$ ${\ Displaystyle R_ {огонь} (т) = {\ гидроразрыва {P_ {шип} (т; \ Delta _ {t})} {\ Delta _ {t}}} = [y (t) + R_ {0}] \ cdot P_ {0} (t)}$

где,

P0 - вероятность того, что нейрон будет "активирован" и готов к срабатыванию. Он задается следующим дифференциальным уравнением:

$P ˙ 0 = - [y (t) + R 0 + R 1] ⋅ P 0 (t) + R 1 {\ displaystyle {\ dot {P}} _ { 0} = - [y (t) + R_ {0} + R_ {1}] \ cdot P_ {0} (t) + R_ {1}}$ ${\ displaystyle {\ dot {P}} _ {0} = - [y (t) + R_ {0} + R_ {1}] \ cdot P_ {0} (t) + R_ {1}}$

P0 обычно можно вычислить рекурсивно с использованием метода Эйлера, но в в случае импульса стимула это дает простое выражение в замкнутой форме.

y (t) является входом модели и интерпретируется как концентрация нейромедиатора в окружающей клетке (в большинстве случаев глутамат). Для внешнего стимула его можно оценить с помощью модели рецепторного слоя:

$y (t) ≃ ggain ⋅ ⟨s 2 (t)⟩ {\ displaystyle y (t) \ simeq g_ {gain} \ cdot \ langle s ^ {2} (t) \ rangle}$ ${\ displaystyle y ( t) \ simeq g_ {усиление} \ cdot \ langle s ^ {2} (t) \ rangle}$ , с $⟨s 2 (t)⟩ {\ displaystyle \ langle s ^ {2} (t) \ rangle}$ ${\ displaystyle \ langle s ^ {2} (t) \ rangle}$ - Кратковременное среднее значение мощности стимула (выраженное в ваттах или другую энергию в единицу времени).

R0 соответствует внутренней скорости спонтанного возбуждения нейрона.
R1 - скорость восстановления нейрона из рефрактерного состояния.

Другие прогнозы этой модели включают:

1) Усредненный потенциал вызванного ответа (ERP), обусловленный популяцией множества нейронов в нефильтрованных измерениях, похож на частоту возбуждения.

2) Изменение напряжения активности из-за активности нескольких нейронов напоминает частоту возбуждения (также известную как мощность нескольких активностей или MUA).

3) Распределение вероятностей между интервалами всплесков принимает форму функции, подобной гамма-распределению.

Экспериментальные данные, подтверждающие модель Nossenson Messer
Свойство модели Носсенсон и Мессер	Ссылки	Описание экспериментальных данных
Форма скорости стрельбы в ответ на импульс слухового стимула		Скорость стрельбы имеет та же форма, что и на рис. 5.
Форма скорости стрельбы в ответ на импульс визуального стимула		Скорость стрельбы имеет ту же форму, что и на рис. 5.
Форма скорости стрельбы в ответ на импульс обонятельного стимула		Скорость стрельбы такая же, как на рис. 5.
Форма скорости стрельбы в ответ на сомато-сенсорный стимул		Скорость возбуждения имеет ту же форму, что и на рис. 5.
Изменение скорости возбуждения в ответ на применение нейромедиатора (в основном глутамата)		Изменение скорости возбуждения в ответ на приложение нейротрансмиттера (Glutamat e)
Квадратная зависимость между давлением слухового стимула и скоростью возбуждения.		Квадратная зависимость между давлением слухового стимула и скоростью возбуждения (- Линейная зависимость в квадрате давления (мощности)).
Квадратная зависимость между электрическим полем визуального стимула (вольты) и интенсивностью возбуждения		Квадратная зависимость между электрическим полем визуального стимула (вольт) - линейная зависимость между визуального стимула и скоростью развития.
Форма статистики межпикового интервала (ISI)		Форма ISI похожа на гамма-функцию
ERP похожа на частоту срабатывания в нефильтрованных измерениях		Форма усредненной вызванной способности в ответ на стимул напоминает темп стрельбы (рис. 5).).
Мощность MUA похожа на частоту возбуждения		Форма эмпирической дисперсии внеклеточных импульсов в ответ на импульс стимула частоту возбуждения (рис. 5).

Немарковские модели

Ниже представлен список опубликованных немарковских моделей нейронов:

Джонсон и Свами
Берри и Мейстер
Касс и Вентура

Моделирование нейронов с фармакологическим входным стимулом

Модели этой категории позволяют делать прогнозы для экспериментов с фармакологической стимуляцией.

Синаптическая передача (Кох и Сегев)

Согласно модели Коха и Сегева, ответ нейрона на отдельные нейротрансмиттеры можно смоделировать как расширение классической модели Ходжкина-Хаксли с как стандартные, так и нестандартные кинетические токи. Четыре нейротрансмиттера в первую очередь на ЦНС. АМРА / каинатные рецепторы являются быстрыми возбуждающими медиаторами, тогда как рецепторы NMDA опосредуют значительно более медленные токи. Быстрые тормозящие токи проходят через ГАМК A рецепторы, а ГАМК B рецепторы опосредуются вторичным G-белком - активированные калиевые каналы. Этот диапазон посредничества дает следующую текущую динамику:

$IAMPA (t, V) = g ¯ AMPA ⋅ [O] ⋅ (V (t) - EAMPA) {\ displaystyle I _ {\ mathrm {AMPA}} (t, V) = {\ bar {g}} _ {\ mathrm {AMPA}} \ cdot [O] \ cdot (V (t) -E _ {\ mathrm {AMPA}})}$ $I _ {{\ mathrm { AMPA}}} (t, V) = {\ bar {g}} _ {{\ mathrm {AMPA}}} \ cdot [O] \ cdot (V (t) -E _ {{\ mathrm {AMPA}} })$
$INMDA (t, V) знак равно г ¯ NMDA ⋅ В (V) ⋅ [O] ⋅ (V (t) - ENMDA) {\ displaystyle I _ {\ mathrm {NMDA}} (t, V) = {\ bar {g}} _ { \ mathrm {NMDA}} \ cdot B (V) \ cdot [O] \ cdot (V (t) -E _ {\ mathrm {NMDA}})}$ $I _ {{\ mathrm {NMDA}}} (t, V) = {\ bar {g}} _ {{\ mathrm {NMDA}}} \ cdot B (V) \ cdot [O] \ cdot (V (t) -E _ {{\ mathrm {NMDA}}}})$
$IGABAA (t, V) = g ¯ GABAA ⋅ ([O 1] + [O 2]) ⋅ (V (t) - EC l) {\ displaystyle I _ {\ mathrm {GABA_ {A}}} (t, V) = {\ bar {g}} _ {\ mathrm {GABA_ {A}}} \ cdot ([O_ {1}] + [O_ {2}]) \ cdot (V (t) -E _ {\ mathrm {Cl}})}$ $I _ {{\ mathrm {GABA_ {A}}}} (t, V) = {\ bar {g}} _ {{\ mathrm {GABA_ {A}}}} \ cdot ([O_ {1}] + [O_ {2}]) \ cdot (V (t) -E _ {{\ mathrm {Cl}}})$
$IGABAB (t, V) знак равно г ¯ GABAB ⋅ [G] N [G] N + K d ⋅ (V (t) - EK) {\ displaystyle I _ {\ mathrm {GABA_ {B}}} (t, V) = {\ bar {g}} _ {\ mathrm {GABA_ {B}}} \ cdot {\ tfrac {[G] ^ {n}} {[G] ^ {n} + K _ {\ mathrm {d }}}} \ cdot (V (t) -E _ {\ mathrm {K}})}$ $I _ {{\ mathrm {GABA_ {B}}}} (t, V) = { \ bar {g}} _ {{\ mathrm {GABA_ {B}}}} \ cdot {\ tfrac {[G] ^ {n}} {[G] ^ {n} + K _ {{\ mathrm {d }}}}} \ cdot (V (t) -E_ {{\ mathrm {K}}})$

где ḡ - максимальная проводимость (около 1 S ), а E - равновесный потенциал данного иона или передатчика (AMDA, NMDA, Cl или K ), а [O] принадлежность открытых рецепторов. Для NMDA существует значительный эффект магниевого блока, который сигмоидально зависит от внутриклеточного магния посредством B (V). Для GABA B, [G] представляет собой концентрацию G-белка, а K d представляет собой диссоциацию G при связывании с воротами калия.

Динамика этой сложной модели была хорошо изучена экспериментально и дает важные результаты с точки зрения очень быстрого синаптического потенцирования и депрессии, то есть быстрого, краткосрочного обучения.

Модель Маркова с двумя состояниями (Носсенсон и Мессер)

Модель Носсенсона и Мессера переводит концентрацию нейротрансмиттера на входной стадии в вероятность высвобождения нейротрансмиттера на выходной стадии. Более подробное описание этой модели см. В разделе Марковская модель с двумя состояниями выше.

Модель нейрона HTM

Модель нейрона HTM была заблокирована Джеффом Хокинсом и исследователями из Numenta и основа теории под названием Иерархическая временная память, описанная в книге Об интеллекте. Он основан на неврологии, а также на физиологии и взаимодействии пирамидных нейронов в неокортексе человеческого мозга..

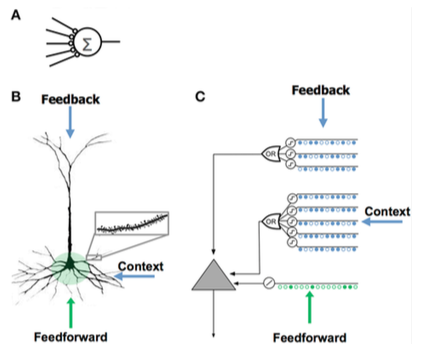Сравнение искусственной нейронной сети (A), биологического нейрона (B) и нейрона HTM (C).

Искусственная нейронная сеть (ANN)

Неокортикальный пирамидный нейрон (биологический Нейрон)

Нейрон модели HTM

- Мало синапсов

- Нет дендритов

- Сумма входных x весов

- Обучается путем изменения весов синапсов

- Тысячи синапсы на дендритах

- Активные дендриты: клетка распознает уникальных паттернов

- Совместная активация набора синапсов на дендритном сегменте вызывает спайк NMDA и деполяризацию в соме

- Источники входных данных в клетку:

входные данные прямого распространения, которые формируют силапсы проксимальнее сомы и напрямую приводят к дополнительным действиям
шипы NMDA, генерируемые в более дистальных базальных
апикальных дендри деполяризация сомнений (обычно недостаточно для генерации соматического действия)

- учится путем выращивания новых синапсов

- вдохновляется пирамидными клетками в слоях неокортекса 2/3 и 5

- Тысячи синапсов

- Активные дендриты: клетка распознает уникальных паттернов

- Моделирует дендриты и пики NMDA с каждым массивом совпадающих детекторов, имеющим набор синапсов

- Обучение моделированию роста новых синапсов

Приложения

Вопрос нейронного моделирования лежит в основе следующих проектов:

Электрический протез сетчатки

Дополнительная литература по этой теме:

нейротрансмиттер протез сетчатки
Дополнительная литература по этой теме:

Кохлеарный имплант

Интерфейс мозг-компьютер

Контроль и ощущения искусственных конечностей

Дополнительная литература по этой теме:

Связь между искусственными и биологическими моделями нейронов

Самая основная модель нейрона из входящего с некоторым вектором синаптического веса и функции активации или передаточной функции внутри выходного сигнала, определяющего нейрон. Это основная структура, используемая для искусственных нейронов, которая в нейронной сети часто выглядит как

$yi = ϕ (∑ jwijxj) {\ displaystyle y_ {i} = \ phi \ left (\ sum _ {j } w_ {ij} x_ {j} \ right)}$ $y_ {i} = \ phi \ left (\ сумма _ {j} w _ {{ij}} x_ {j} \ right)$

где y i - выход i-го нейрона, x j - сигнал j-го входного нейрона, w ij - синаптический вес (или сила связи) между нейронами i и j, а φ - функция активации. Хотя эта модель успешно используется в приложениях для машинного обучения, она не подходит для реальных (биологических) нейронов, поскольку в ней отсутствует зависимость от времени, демонстрируют спайки реальных нейронов. Именно такую форму принимают биологические модели типа «объединяй и огонь»; в и фармакологической литературе медицинской степени заменены кинетическими моделями, такими как модель Ходжки - Хаксли.

В случае моделирования биологического нейрона вместо абстракций, таких как «вес» и «», используются физические аналоги. Возбуждение нейрона включает движение в клетку, функцию передачи ". Нейрон заполнен и окружен водой, содержащей ионы, несущие электрические заряды. Нейрон из совместимой клеточной мембраной и может поддерживать заряженных других сторон, которая определяет емкость Cm. Это происходит, когда нейротрансмиттеры вызывают открытие ионных каналов на клеточной мембране. Мы описываем это физическим зависящим от времени током I (t).>напряжение или разности электрической мощности между окружающей средой, что иногда приводит к скачку напряжения , называемому потенциалом действия, проходит по длине клетки и запускает высвобождение дополнительных нейротрансмиттеров Таким образом, напряжение является величиной, представляющей интерес, и определяется как V m (t).

Предположения относительно роли нейрона в более широком контенте ексте принципа работы мозга

Схема обнаружения энергии на основе нейротрансмиттеров

Схема обнаружения энергии на основе нейротрансмиттеров предполагает, что нервная ткань химически функционирует обнаружение, подобную радиолокационную.

Рис. 6 Схема биологического нейронного обнаружения, предложенная Носсенсоном и др.

Как показано на рис. 6, основная идея гипотезы состоит в том, чтобы учитывать концентрацию нейротрансмиттера, генерацию нейротрансмиттера и скорость удаления нейротрансмиттера как важные величины при выполнении задачи обнаружения., относящимся к измеренным электрическим параметрам как к побочному эффекту, который только определенным условиям совпадает с функциональным назначением каждого шага. Схема включения на радароподобное «обнаружение энергии», потому что она включает в себя возведение сигнала в квадрат, временное суммирование и механизм переключения порогов, как и детектор энергии, но также включает блок, который выделяет стимулы стимула и переменную длину (переменная память). Согласно этой гипотезе, физиологическим эквивалентом статистики энергетического теста является нейротрансмиттера, а скорость возбуждения соответствует току нейротрансмиттера. Эта интерпретация состоит в том, что она приводит к единому последовательному объяснению, позволяет проводить электрофизиологические измерения, биохимические измерения и психофизические результаты.

Доказательства, рассмотренные в предположении следующая связь между функциональностью и гистологической классификацией:

Возведение в квадрат стимула, вероятно, выполнено рецепторными клетками.
Подчеркивание краев стимула и передача сигнала осуществляется нейронами.
Накопление нейромедиаторов во времени осуществляется глиальными клетками. Кратковременное накопление нейротрансмиттеров также может происходить в некоторых типах нейронов.
Логическое переключение осуществляется глиальными клетками, и оно является результатом превышения порогового уровня нейромедиатора. Это превышение порога также сопровождается изменением скорости утечки нейромедиаторов.
Физическое переключение движения «все или без него» происходит из-за мышечных клеток и является результатом превышения определенного порога нейромедиаторов в окружении мышц.

Примечание. что, хотя электрофизиологические сигналы на рисунке 6 часто похожи на функциональный сигнал (мощность сигнала / уровень нейромедиатора / мышечная сила), есть некоторые этапы, на которых электрическое наблюдение отличается от функционального назначения соответствующего этапа. В частности, Носсенсон и др. предположили, что пересечение порога глии имеет совершенно другое функциональное действие по с излучаемым электрофизиологическим сигналом, и что последнее может быть только побочным эффектом разрыва глии.

Общие комментарии относительно современных научных и инженерных моделей

Приведенные выше модели все еще являются идеализацией. Необходимо внести поправки на увеличенную площадь поверхности мембраны, обусловленную многочисленными дендритными шипами, значительно более высокими, чем экспериментальные данные при комнатной температуре, и неоднородностью внутренней структуры клетки. Некоторые наблюдаемые эффекты не укладываются в некоторых из этих моделей. Например, циклическое изменение температуры (с минимальным повышением чистой температуры) клеточной мембраны во время использования функции несовместимо с моделями, которые используют моделирование мембраны как сопротивление, которое должно рассеивать энергию, когда через нее протекает ток. Переходное утолщение клеточной мембраны во время использования также предсказывается этими моделями, как и изменение в результате этого утолщения, не включены в эти модели. Действие некоторых анестетиков, таких как инертные газы, также проблематично для этих моделей. Новые модели, такие как солитонная модель, пытаются объяснить эти явления, но они менее развиты, чем старые модели, и еще не получили широкого применения.
Современные взгляды на роль науки модель предполагает, что «все модели ошибочны, но некоторые полезны» (Box and Draper, 1987; Gribbin, 2009; Paninski et al., 2009).
Недавнее предположение предполагает, что каждый нейрон может функционировать как независимые пороговые устройства. Предполагается, что нейрон может быть анизотропно активирован по происхождению сигналов, поступающих к мембране, через его дендритные деревья. Было предложено, чтобы импульсная форма волны зависела от источника стимула.

См. Также

Ссылки