Сигмоидальная функция

Математическая функция, имеющая характеристическую S-образную кривую или сигмовидную кривую логистическая кривая 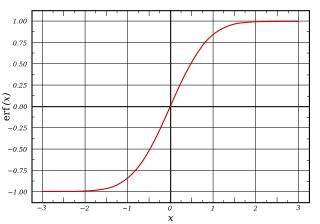График функция ошибок

A сигмоидальная функция является математической функцией, имеющей характеристическую "S"-образную кривую или сигмовидную кривую . Типичным примером сигмоидной функции является логистическая функция, показанная на первом рисунке и определяемая формулой:

$S\; (x)\; =\; 1\; 1\; +\; e\; -\; x\; =\; e\; x\; e\; x\; +\; 1.\; \{\backslash \; displaystyle\; S\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{1\; +\; e\; ^\; \{-\; x\}\}\}\; =\; \{\backslash \; frac\; \{e\; ^\; \{x\}\}\; \{e\; ^\; \{x\}\; +1\}\}.\}$

Другие стандартные сигмоидальные функции приведены в разделе Примеры.

. Особые случаи сигмоидной функции включают кривую Гомперца (используется в системах моделирования, которые насыщаются при больших значениях x) и кривая (используется в водосбросе некоторых плотин ). Сигмоидальные функции имеют домен всех вещественных чисел, при этом возвращаемое (ответное) значение обычно монотонно увеличивается, но может уменьшаться. Сигмоидальные функции чаще всего показывают возвращаемое значение (ось y) в диапазоне от 0 до 1. Другой часто используемый диапазон - от -1 до 1.

Широкий спектр сигмовидных функций, включая логистические и гиперболические. тангенциальные функции использовались как функция активации для искусственных нейронов. Сигмовидные кривые также распространены в статистике как кумулятивные функции распределения (которые меняются от 0 до 1), такие как интегралы логистической плотности, нормальной плотности, и t функции плотности вероятности Стьюдента. Логистическая сигмоидальная функция обратима, а ее обратная функция - logit.

Содержание

• 1 Определение
• 2 Свойства
• 3 Примеры
• 4 Приложения
• 5 См. Также
• 6 Ссылки

Определение

Сигмоидная функция - это ограниченная, дифференцируемая, действительная функция, которая определена для всех реальных входных значений и имеет неотрицательную производную в каждой точке и ровно одну точку перегиба. Сигмовидная «функция» и сигмовидная «кривая» относятся к одному и тому же объекту.

Свойства

В общем, сигмоидальная функция является монотонной и имеет первую производную, которая имеет форму колокола. И наоборот, интеграл любой непрерывной неотрицательной колоколообразной функции (с одним локальным максимумом и без локального минимума, если только он не вырожден) будет сигмоидальным. Таким образом, кумулятивные функции распределения для многих обычных распределений вероятностей являются сигмоидальными. Одним из таких примеров является функция ошибок , которая связана с кумулятивной функцией распределения нормального распределения.

. Сигмоидальная функция ограничена парой горизонтальных асимптот как $x\; \to \; \pm \; \infty \; \{\backslash \; displaystyle\; x\; \backslash \; rightarrow\; \backslash \; pm\; \backslash \; infty\}$.

сигмовидная функция выпуклая для значений меньше 0 и вогнутая для значений больше 0.

Примеры

Сравнение некоторых сигмовидных функций. На чертеже все функции нормализованы таким образом, что их наклон в начале координат равен 1.

• Логистическая функция

$f\; (x)\; =\; 1\; 1\; +\; e\; -\; x\; \{\backslash \; displaystyle\; f\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{1\; +\; e\; ^\; \{-\; x\}\}\}\}$

• Гиперболический тангенс (смещенная и масштабированная версия логистической функции, см. Выше)

$f\; (x)\; =\; tanh\; \; x\; =\; ex\; -\; e\; -\; xex\; +\; e\; -\; x\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; tanh\; x\; =\; \{\backslash \; frac\; \{e\; ^\; \{x\}\; -e\; ^\; \{-\; x\}\}\; \{e\; ^\; \{x\}\; +\; e\; ^\; \{-\; x\}\}\}\; \}$

• Функция арктангенса

$f\; (x)\; =\; arctan\; \; x\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; arctan\; x\}$

• функция Гудермана

$f\; (x)\; =\; gd\; \; (x)\; =\; \int \; 0\; Икс\; 1\; cosh\; \; tdt\; =\; 2\; arctan\; \; (tanh\; \; (x\; 2))\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; operatorname\; \{gd\}\; (x)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{x\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; ch\; t\}\}\; \backslash ,\; dt\; =\; 2\; \backslash \; arctan\; \backslash \; left\; (\backslash \; tanh\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\}$

• Функция ошибок

$f\; (x)\; знак\; равно\; erf\; \; (x)\; знак\; равно\; 2\; \pi \; \int \; 0\; xe\; -\; t\; 2\; dt\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; operatorname\; \{erf\}\; (x)\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{x\}\; e\; ^\; \{-\; t\; ^\; \{2\}\}\; \backslash ,\; dt\}$

• Обобщенная логистическая функция

$f\; (x)\; =\; (1\; +\; e\; -\; x)\; -\; \alpha ,\; \alpha >0\; \{\; \backslash \; Displaystyle\; е\; (х)\; =\; (1\; +\; е\; ^\; \{-\; х\})\; ^\; \{-\; \backslash \; альфа\},\; \backslash \; quad\; \backslash \; alpha>0\}$

• Smoothstep function

$f\; (x)\; =\; \{(\int \; 0\; 1\; (1\; -\; u\; 2)\; N\; du)\; -\; 1\; \int \; 0\; x\; (1\; -\; u\; 2)\; N\; du,\; |\; х\; |\; \le \; 1\; знак\; \; (x)\; |\; х\; |\; \ge \; 1\; N\; \ge \; 1\; \{\backslash \; Displaystyle\; е\; (Икс)\; =\; \{\backslash \; begin\; \{cases\}\; \backslash \; Displaystyle\; \{\backslash \; left\; (\backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; (1-u\; ^\; \{2\})\; ^\; \{N\}\; \backslash \; du\; \backslash \; right)\; ^\; \{-\; 1\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{x\}\; (1-u\; ^\; \{2\})\; ^\; \{N\}\; \backslash \; du\},\; |\; x\; |\; \backslash \; leq\; 1\; \backslash \backslash \backslash \backslash \backslash \; имя\; оператора\; \{sgn\; \}\; (x)\; |\; x\; |\; \backslash \; geq\; 1\; \backslash \backslash \backslash \; end\; \{cases\}\}\; \backslash ,\; \backslash \; quad\; N\; \backslash \; geq\; 1\}$

• Некоторые алгебраические функции, например

$f\; (x)\; =\; x\; 1\; +\; x\; 2\; \{\backslash \; displaystyle\; f\; (x)\; =\; \{\backslash \; frac\; \{x\}\; \{\backslash \; sqrt\; \{1\; +\; x\; ^\; \{2\}\}\}\}\}$

Приложения

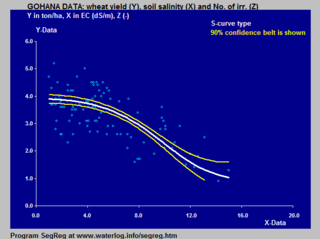Перевернутая логистическая S-кривая для моделирования связь урожайности пшеницы с засолением почвы.

Многие естественные процессы, такие как сложные системы кривые обучения, демонстрируют прогрессию с малого, которая со временем ускоряется и приближается к кульминации. Когда конкретная математическая модель отсутствует, часто используется сигмовидная функция.

Модель ван Генухтена – Гупты основана на перевернутой S-образной кривой и применяется к реакции урожайности сельскохозяйственных культур на засоление почвы.

Примеры применения логистической S-кривой к ответу урожайности (пшеницы) как на засоленность почвы, так и на глубину уровня грунтовых вод в почве показаны в логистическая функция # В сельском хозяйстве: моделирование реакции сельскохозяйственных культур.

В искусственных нейронных сетях для повышения эффективности иногда вместо этого используются негладкие функции; они известны как жесткие сигмоиды.

В обработке аудиосигналов сигмоидальные функции используются как waveshaper передаточные функции для имитации звука аналоговая схема отсечение.

В биохимии и фармакологии уравнение Хилла и уравнение Хилла – Ленгмюра являются сигмоидными функциями.

В компьютерной графике и рендеринге в реальном времени некоторые сигмовидные функции используются для плавного смешивания цветов или геометрии между двумя значениями без видимых стыков или разрывов.

См. Также

Викискладе есть материалы, связанные с сигмоидными функциями.

• ступенчатой ​​функцией Хевисайда
• Логистическая регрессия
• Логит
• Функция Softplus
• модифицированный гиперболический тангенс Соболевой
• Функция Softmax
• Функция Swish
• Распределение Вейбулла
• Статистика Ферми – Дирака

Ссылки

• Mitchell, Tom M. (1997). Машинное обучение. WCB – McGraw – Hill. ISBN 978-0-07-042807-2.. В частности, см. «Главу 4: Искусственные нейронные сети» (в частности, стр. 96–97), где Митчелл использует слова «логистическая функция» и «сигмовидная функция» как синонимы - эту функцию он также называет «функцией сжатия» - и сигмоидальная (также известная как логистическая) функция используется для сжатия выходных сигналов «нейронов» в многослойных нейронных сетях.
• Хамфрис, Марк. «Непрерывный вывод, сигмоидальная функция».Свойства сигмоида, включая то, как он может сдвигаться по осям и как его домен может быть преобразован.