Войти
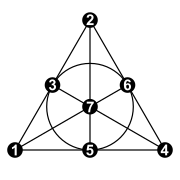
Плоскость Фано В конечной геометрии, Плоскость Фано (после Джино Фано ) - это конечная проективная плоскость порядка 2. Это конечная проективная плоскость с наименьшим возможным числом точек и прямых: 7 точек и 7 линий, по 3 точки на каждой линии и 3 линии через каждую точку. Стандартное обозначение этой плоскости как члена семейства проективных пространств - это PG (2, 2), где PG означает «проективная геометрия », первым параметром является геометрический размер и второй параметр - порядок.
Плоскость Фано является примером конечной структуры падения, поэтому многие из ее свойств могут быть установлены с помощью комбинаторных методов и других инструментов, используемых при изучении геометрии падения. Поскольку это проективное пространство, алгебраические методы также могут быть эффективными инструментами в его изучении.
Плоскость Фано может быть построена с помощью линейной алгебры как проективная плоскость над конечным полем с двумя элементами. Аналогичным образом можно построить проективные плоскости над любым другим конечным полем, причем плоскость Фано является наименьшей.
Используя стандартную конструкцию проективных пространств через однородные координаты, семь точек плоскости Фано могут быть помечены семью ненулевыми упорядоченными тройками двоичных цифр 001, 010, 011, 100, 101, 110 и 111. Это можно сделать таким образом, чтобы для каждых двух точек p и q третья точка на линии pq имела метку, образованную добавлением меток p и q по модулю 2. Другими словами, точки плоскости Фано соответствуют ненулевым точкам конечного векторного пространства размерности 3 над конечным полем порядка 2.
Благодаря этой конструкции плоскость Фано считается плоскостью Дезарга, даже если плоскость слишком мала, чтобы содержать невырожденную конфигурацию Дезарга (которая требует 10 точек и 10 линий).
Линии плоскости Фано также могут иметь однородные координаты, опять же с использованием ненулевых троек двоичных цифр. В этой системе координат точка попадает в линию, если координата точки и координата линии имеют четное количество позиций, в которых они оба имеют ненулевые биты: например, точка 101 принадлежит линии 111, потому что они имеют ненулевые биты в двух общих позициях. В терминах базовой линейной алгебры точка принадлежит линии, если внутреннее произведение векторов, представляющих точку и линию, равно нулю.
Линии можно разделить на три типа.
Альтернативно, 7 точек плоскости соответствуют 7 неидентификационным элементам группы (Z2) = Z 2 × Z 2 × Z 2. Линии плоскости соответствуют подгруппам порядка 4, изоморфных Z 2 × Z 2. группа автоморфизмов GL (3,2) группы (Z 2) является группой плоскости Фано и имеет порядок 168.
Двудольный граф Хивуда. Точки представлены вершинами одного цвета, а линии - вершинами другого цвета. Как и любая структура инцидентности, граф Леви плоскости Фано является двудольным графом, вершины одной части представляют точки, а другая - линии, причем две вершины соединены, если соответствующая точка и линия инцидентны. Этот конкретный граф представляет собой связный кубический граф (регулярный степени 3), имеет обхват 6 и каждая часть содержит 7 вершин. Это граф Хивуда, уникальный 6-клеточный.
Коллинеация плоскости Фано, соответствующая 3-битной перестановке кода Грея A коллинеарность, автоморфизм или симметрия плоскости Фано - это перестановка 7 точек, которая сохраняет коллинеарность: то есть она несет коллинеарных точек (на той же линии) в коллинеарные точки. Согласно основной теореме проективной геометрии, полная группа коллинеаций (или группа автоморфизмов, или группа симметрии ) является проективная линейная группа PGL (3,2), также обозначается 
Это хорошо известная группа порядка 168 = 2 · 3 · 7, вторая по величине неабелева простая группа после A5 порядка 60.
Поскольку группа перестановок действует на 7 точек плоскости, группа коллинеаций дважды транзитивна означает, что любая упорядоченная пара точек может быть сопоставлена по крайней мере одной коллинеацией с любой другой упорядоченной парой точек. (См. Ниже.)
Коллинеации также можно рассматривать как сохраняющие цвет автоморфизмы графа Хивуда (см. Рисунок).
Двойственность в плоскости Фано: каждая точка соответствует линии и наоборот. A биекция между множеством точек и множеством линий, сохраняющим инцидентность, называется двойственностью и двойственностью порядка. два называется полярностью.
Двойственности можно рассматривать в контексте графа Хивуда как автоморфизмы, обращающие цвет. Пример полярности дается отражением через вертикальную линию, которая делит пополам графическое представление Хивуда, приведенное справа. Наличие этой полярности показывает, что плоскость Фано самодуальна. Это также является непосредственным следствием симметрии между точками и линиями в определении отношения инцидентности в терминах однородных координат, как подробно описано в предыдущем разделе.
A nimber нумерация плоскости Фано Группа коллинеаров, представленная как группа перестановок из 7 точек, пронумерованных на рисунке, генерируется с помощью:
Включает 6 классов сопряженности. Каждая из следующих структур цикла определяет один класс сопряженности:
Идентификационная перестановка
21 перестановка с двумя 2-циклами 
42 перестановки с 4-циклом и 2- цикл
56 перестановок с двумя 3-циклами48 перестановок с полным 7-циклом образуют два различных класса сопряженности с 24 элементами:
A отображается в B, B в C, C в D. Тогда D находится на той же линии, что и A и B.
A отображается на B, B в C, C в D. Тогда D находится на той же линии, что и A и C.См. коллинеации плоскостей Фано полный список.
Следовательно, согласно теореме перечисления Полиа, количество неэквивалентных раскрасок плоскости Фано в n цветов составляет:
В любой проективной плоскости набор из четырех точек, никакие три из которых не коллинеарны, и шесть прямых, соединяющих пары этих точек, представляют собой конфигурацию, известную как полный четырехугольник. Линии называются сторонами, а пары сторон, не пересекающиеся в одной из четырех точек, называются противоположными сторонами. Точки, в которых встречаются противоположные стороны, называются диагональными точками, и их три.
Если эта конфигурация лежит в проективной плоскости и три диагональные точки коллинеарны, то семь точек и семь линий развернутого Конфигурация образуют подплоскость проективной плоскости, которая изоморфна плоскости Фано и называется подплоскостью Фано.
Известный результат, полученный благодаря Эндрю М. Глисону, утверждает, что если каждый полный четырехугольник в конечной проективной плоскости продолжается до подплоскости Фано (то есть имеет коллинеарные диагональные точки), то плоскость является дезарговским. Глисон назвал любую проективную плоскость, удовлетворяющую этому условию, плоскостью Фано, что вызвало некоторую путаницу с современной терминологией. Чтобы усугубить путаницу, аксиома Фано утверждает, что диагональные точки полного четырехугольника никогда не коллинеарны, и это условие выполняется в евклидовой и реальной проективной плоскостях. Таким образом, то, что Глисон называл плоскостями Фано, не удовлетворяет аксиоме Фано.
Плоскость Фано содержит следующее количество конфигураций точек и линий разных типов. Для каждого типа конфигурации количество копий конфигурации, умноженное на количество симметрий плоскости, которые сохраняют конфигурацию неизменной, равно 168, размеру всей группы коллинеации, при условии, что каждая копия может быть сопоставлена с любой другой копией ( см. Теорема о стабилизаторе орбиты ). Поскольку плоскость Фано самодуальна, эти конфигурации входят в двойные пары, и можно показать, что количество коллинеаций, фиксирующих конфигурацию, равно количеству коллинеаций, фиксирующих ее двойную конфигурацию.
троек точек, семь из которых являются коллинеарными тройками, оставляя 28 неколлинеарных троек или треугольников. Конфигурация, состоящая из трех точек треугольника и трех линий, соединяющих пары этих точек, представлена 6-циклом в графе Хивуда. Сохраняющий цвет автоморфизм графа Хивуда, фиксирующий каждую вершину 6-цикла, должен быть тождественным автоморфизмом. Это означает, что имеется 168 помеченных треугольников, фиксированных только тождественной коллинеацией, и только шесть коллинеаций, которые стабилизируют немаркированный треугольник, по одной для каждой перестановки точек. Эти 28 треугольников можно рассматривать как соответствующие 28 битангенсам квартики. Существует 84 способа указать треугольник вместе с одной выделенной точкой на этом треугольнике и двумя симметриями, фиксирующими эту конфигурацию. Двойная конфигурация треугольника также является треугольником.Плоскость Фано является примером (n 3) - конфигурация, то есть набор из n точек и n линий с тремя точками на каждой линии и тремя линиями через каждую точку. Плоскость Фано, конфигурация (7 3), уникальна и является наименьшей такой конфигурацией. Согласно теореме Стейница конфигурации этого типа могут быть реализованы в евклидовой плоскости, имеющей не более одной изогнутой линии (все остальные линии лежат на евклидовых линиях).
Плоскость Фано представляет собой небольшой симметричный блок, в частности 2- (7,3,1) -конструкции. Точки рисунка - это точки плоскости, а блоки рисунка - это линии плоскости. Таким образом, это ценный пример в теории (блочного) дизайна.
С точками, обозначенными 0, 1, 2,..., 6, линии (как наборы точек) являются сдвигами (7, 3, 1) плоского разностного набора, заданного на {0, 1, 3} в группе 
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| ℓ0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| ℓ1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| ℓ2 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| ℓ3 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| ℓ4 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| ℓ5 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| ℓ6 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
Плоскость Фано, как блочная конструкция, является системой троек Штейнера. Таким образом, ей может быть придана структура квазигруппы . Эта квазигруппа совпадает с мультипликативной структурой, определяемой единицей октонионы e1, e 2,..., e 7 (опуская 1), если знаки октониона продукты игнорируются (Baez 2002).
Плоскость Фано - один из важных примеров структурной теории матроидов. Исключение плоскости Фано как минор матроидов необходимо для характеристики нескольких важных классов матроидов, таких как обычные, графические и графические.
Если вы разделите одну линию на три двухточечных, вы получите «конфигурацию не Фано», которую можно встроить в реальную плоскость. Это еще один важный пример в теории матроидов, поскольку он должен быть исключен для выполнения многих теорем.
Плоскость Фано может быть расширена в третьем измерении, чтобы сформировать трехмерное проективное пространство, обозначенное PG (3,2) . Оно имеет 15 точек, 35 линий и 15 плоскостей и является наименьшим трехмерным проективным пространством. Он также имеет следующие свойства:
 | Викискладе есть медиафайлы, относящиеся к плоскости Фано. |
