Войти
В компьютерной графике, Slerp - это сокращение от сферической линейной интерполяции, введенное Кеном Шумейком в контексте кватерниона интерполяции с целью анимации 3D вращение. Это относится к движению с постоянной скоростью по дуге единичного радиуса большого круга, учитывая концы и параметр интерполяции от 0 до 1.
Слерп имеет геометрическую формулу, не зависящую от кватернионов и размерность пространства, в котором находится дуга. встроенный. Эта формула, симметричная взвешенная сумма, приписанная Гленну Дэвису, основана на том факте, что любая точка кривой должна быть линейной комбинацией концов. Пусть p 0 и p 1 будут первой и последней точками дуги, и пусть t будет параметром, 0 ≤ t ≤ 1. Вычислить Ω как угол . дугой, так что cos Ω = p 0 ∙ p 1, n-мерное скалярное произведение единичных векторов от начала до концы. Геометрическая формула тогда
![{\ displaystyle \ operatorname {Slerp} (p_ {0}, p_ {1}; t) = {\ frac {\ sin {[(1-t) \ Omega}]} {\ sin \ Омега}} p_ {0} + {\ frac {\ sin [t \ Omega]} {\ sin \ Omega}} p_ {1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1004f9b8696aaab7419dd74405bb96fd2c3adef8)
Симметрия заключается в том, что 
Путь Slerp: фактически, сферическая геометрия эквивалентна пути вдоль отрезка прямой на плоскости; большой круг - сферический геодезический.
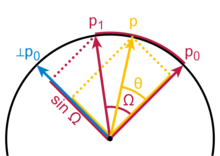Наклонный вектор выпрямляется до фактора Слерпа. Более знакомый, чем общая формула Слерпа, случай, когда конечные векторы перпендикулярны, и в этом случае формула p 0 cos θ + p 1 sin θ. Если положить θ = t π / 2 и применить тригонометрическое тождество cos θ = sin (π / 2 - θ), это станет формулой Слерпа. Коэффициент 1 / sin Ω в общей формуле является нормализацией, поскольку вектор p 1 под углом Ω к p 0 проецируется на перпендикуляр ⊥p 0 длиной только sin Ω.
Некоторые частные случаи Slerp допускают более эффективный расчет. Когда на растровом изображении должна быть нарисована дуга окружности, предпочтительным методом является некоторый вариант алгоритма круга Брезенхема. Оценка при значениях специального параметра 0 и 1 тривиально дает p 0 и p 1 соответственно; и деление пополам, оценка на 1/2, упрощается до (p 0 + p 1) / 2, нормализовано. Другой частный случай, распространенный в анимации, - оценка с фиксированными концами и равными параметрическими шагами. Если p k − 1 и p k - два последовательных значения, и если c - удвоенное их скалярное произведение (постоянное для всех шагов), то следующее значение p k +1, это отражение p k + 1 = cp k - p k − 1.
Когда Slerp применительно к модулю кватернионы, путь кватерниона отображается на путь через трехмерные вращения стандартным способом . Эффект представляет собой вращение с постоянной угловой скоростью вокруг фиксированной оси вращения. Когда начальной конечной точкой является тождественный кватернион, Слерп дает сегмент однопараметрической подгруппы из группы Ли трехмерных вращений, SO (3), и ее универсальная накрывающая группа единичных кватернионов, S. Slerp дает самый прямой и кратчайший путь между конечными точками кватерниона и сопоставляется с поворотом на угол 2Ω. Однако, поскольку покрытие двойное (q и -q соответствуют одному и тому же вращению), траектория вращения может поворачиваться либо на «короткий путь» (менее 180 °), либо на «длинный путь» (более чем на 180 °). Если скалярное произведение, cos Ω, отрицательно, можно предотвратить использование длинных путей путем отрицания одного конца, таким образом гарантируя, что −90 ° ≤ Ω ≤ 90 °.
У Слерпа также есть выражения в терминах алгебры кватернионов, все с использованием возведения в степень. Действительные степени кватерниона определяются в терминах экспоненциальной функции кватерниона , записываемой как e и задаваемой степенным рядом, одинаково хорошо знакомым из исчисления, комплексного анализа и матричная алгебра:
Запись единичного кватерниона q в форме versor, cos Ω + v sin Ω, с v единичный 3-вектор, и, учитывая, что квадрат кватерниона v равен -1 (что подразумевает кватернионную версию формулы Эйлера ), мы имеем e = q и q = cos t Ω + v sin t Ω. Представляющая интерес идентификация q = q 1q0, так что действительная часть q равна cos Ω, так же, как геометрическое скалярное произведение, используемое выше. Вот четыре эквивалентных кватернионных выражения для Slerp.
![{\ displaystyle {\ begin {align} \ operatorname {Slerp} (q_ {0}, q_ {1}, t) = q_ {0} (q_ {0} ^ {- 1} q_ {1}) ^ {t} \\ [6pt] = q_ {1} (q_ {1} ^ {- 1} q_ {0}) ^ {1-t} \\ [6pt] = (q_ { 0} q_ {1} ^ {- 1}) ^ {1-t} q_ {1} \\ [6pt] = (q_ {1} q_ {0} ^ {- 1}) ^ {t} q_ { 0} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/179c6c90dc1f8ed76a220c1e84b44b6867fdfa2b)
производная от Slerp (q 0, q 1 ; t) относительно t, предполагая, что концы зафиксированы, является log (q 1q0), умноженным на значение функции, где кватернион натуральный логарифм в этом случае дает половину 3D угловой скорости вектор. Начальный касательный вектор переносится параллельно к каждой касательной вдоль кривой; таким образом, кривая действительно является геодезической.
В касательном пространстве в любой точке кватернионной кривой Слерпа, инверсия экспоненциальной карты преобразует кривую в линейный сегмент. Кривые Слерпа, не проходящие через точку, не могут трансформироваться в линии в касательном пространстве этой точки.
Quaternion Slerps обычно используются для построения гладких анимационных кривых путем имитации аффинных конструкций, таких как алгоритм де Кастельжау для кривых Безье. Поскольку сфера не является аффинным пространством, знакомые свойства аффинных конструкций могут не работать, хотя построенные кривые в противном случае могут быть полностью удовлетворительными. Например, алгоритм де Кастельжау может использоваться для разделения кривой в аффинном пространстве; это не работает на сфере.
Двузначный Slerp может быть расширен для интерполяции среди многих единичных кватернионов, но расширение теряет фиксированное время выполнения алгоритма Slerp.
Приведенный ниже код C ++ иллюстрирует реализацию алгоритма Slerp, который обрабатывает некоторые общие крайние случаи.
Quaternion slerp (Quaternion v0, Quaternion v1, double t) {// Только кватернионы единиц являются допустимыми вращениями. // Нормализовать, чтобы избежать неопределенного поведения. v0.normalize (); v1.normalize (); // Вычислить косинус угла между двумя векторами. двойная точка = dot_product (v0, v1); // Если скалярное произведение отрицательное, slerp не выберет // более короткий путь. Обратите внимание, что v1 и -v1 эквивалентны, когда // отрицание применяется ко всем четырем компонентам. Исправить // изменением одного кватерниона. if (dot < 0.0f) { v1 = -v1; dot = -dot; } const double DOT_THRESHOLD = 0.9995; if (dot>DOT_THRESHOLD) {// Если входы слишком близки для удобства, // линейно интерполируем и нормализуем результат. Результат кватерниона = v0 + t * (v1 - v0); result.normalize (); вернуть результат; } // Поскольку точка находится в диапазоне [0, DOT_THRESHOLD], acos безопасен double theta_0 = acos (dot); // theta_0 = угол между входными векторами double theta = theta_0 * t; // theta = угол между v0 и результатом double sin_theta = sin (theta); // вычисляем это значение только один раз double sin_theta_0 = sin (theta_0); // вычисляем это значение только один раз double s0 = cos (theta) - dot * sin_theta / sin_theta_0; // == sin (theta_0 - theta) / sin (theta_0) double s1 = sin_theta / sin_theta_0; возврат (s0 * v0) + (s1 * v1); }Ниже приводится тот же алгоритм, за исключением Python. Он использует NumPy и может вычислять множественные интерполяции slerp между двумя кватернионами.
импортировать numpy как np def slerp (v0, v1, t_array): "" "Сферическая линейная интерполяция." "" #>>>slerp ([1,0,0,0], [0,0,0, 1], np.arange (0, 1, 0.001)) t_array = np.array (t_array) v0 = np.array (v0) v1 = np.array (v1) dot = np.sum (v0 * v1) if dot < 0.0: v1 = -v1 dot = -dot DOT_THRESHOLD = 0.9995 if dot>DOT_THRESHOLD: результат = v0 [np.newaxis,:] + t_array [:, np.newaxis] * (v1 - v0) [np.newaxis,:] return (result.T / np.linalg.norm (результат, ось = 1)). T theta_0 = np.arccos (точка) sin_theta_0 = np.sin (theta_0) theta = theta_0 * t_array sin_theta = np.sin (theta) s0 = np.cos (theta) - dot * sin_theta / sin_theta_0 s1 = sin_theta / sin_theta_0 return (s0 [:, np.newaxis] * v0 [np.newaxis,:]) + (s1 [:, np.newaxis] * v1 [np.newaxis,:])
