Последовательность с низким расхождением

В математике последовательность с низким расхождением - это последовательность, обладающая тем свойством, что для всех значений N ее подпоследовательность x 1,..., x N имеет низкое расхождение.

Грубо говоря, несоответствие последовательности является низким, если доля точек в последовательности, попадающей в произвольное множестве B близка к пропорциональна степени из B, так как будет происходить в среднем (но не для конкретных образцов) в случае равнораспределен последовательность. Конкретные определения несоответствия различаются в зависимости от выбора B ( гиперсферы, гиперкубы и т. Д.) И того, как вычисляется (обычно нормализуется) и комбинируется несоответствие для каждого B (обычно с использованием наихудшего значения).

Последовательности с низким расхождением также называются квазислучайными последовательностями из-за их общего использования в качестве замены равномерно распределенных случайных чисел. Модификатор «квази» используется для более четкого обозначения того, что значения последовательности с низким расхождением не являются ни случайными, ни псевдослучайными, но такие последовательности обладают некоторыми свойствами случайных величин, а в некоторых приложениях, таких как метод квази-Монте-Карло, их меньшее расхождение. это важное преимущество.

• 1 Приложения
  • 1.1 Последовательности с низким расхождением при численном интегрировании
• 2 Определение несоответствия
• 3 Неравенство Коксмы – Главки
• 4 Формула Главки – Зарембы
• 5 версия неравенства Коксма-Hlawka${\ displaystyle L ^ {2}}$
• 6 Неравенство Эрдеша – Турана – Коксмы.
• 7 Основные домыслы
• 8 Нижние оценки
• 9 Построение последовательностей с малым расхождением
  • 9.1 Случайные числа
  • 9.2 Аддитивное повторение
  • 9.3 последовательность ван дер Корпута
  • 9.4 Последовательность Холтона
  • 9.5 Набор Хаммерсли
  • 9.6 Последовательность Соболя
  • 9.7 Отбор проб диска Пуассона
• 10 графических примеров
• 11 См. Также
• 12 Примечания
• 13 Ссылки
• 14 Внешние ссылки

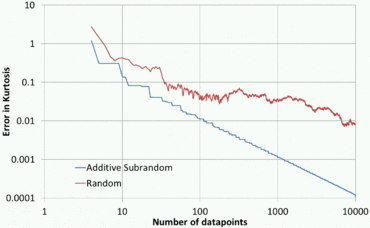Ошибка в оценке эксцесса как функции количества точек данных. «Аддитивная квазислучайность» дает максимальную ошибку, когда c  = ( √ 5  - 1) / 2. «Случайный» дает среднюю ошибку по шести сериям случайных чисел, где среднее значение берется для уменьшения величины диких колебаний.

Квазислучайные числа имеют преимущество перед чистыми случайными числами в том, что они быстро и равномерно покрывают интересующую область. У них есть преимущество перед чисто детерминированными методами в том, что детерминированные методы дают высокую точность только тогда, когда количество точек данных предварительно установлено, тогда как при использовании квазислучайных последовательностей точность обычно постоянно повышается по мере добавления дополнительных точек с полным повторным использованием существующих точек. С другой стороны, квазислучайные наборы точек могут иметь значительно меньшее расхождение для заданного числа точек, чем чисто случайные последовательности.

Два полезных приложений находятся в поиске характеристической функции в виде функции плотности вероятности, и при нахождении производной функции детерминированной функции с небольшим количеством шума. Квазислучайные числа позволяют очень быстро вычислять моменты более высокого порядка с высокой точностью.

Приложения, которые не включают сортировку, заключаются в нахождении среднего, стандартного отклонения, асимметрии и эксцесса статистического распределения, а также в нахождении интегральных и глобальных максимумов и минимумов сложных детерминированных функций. Квазислучайные числа также могут использоваться для обеспечения отправных точек для детерминированных алгоритмов, которые работают только локально, например, итерация Ньютона – Рафсона.

Квазислучайные числа также можно комбинировать с алгоритмами поиска. Алгоритм в стиле быстрой сортировки двоичного дерева должен работать исключительно хорошо, потому что квазислучайные числа сглаживают дерево намного лучше, чем случайные числа, и чем более плоское дерево, тем быстрее выполняется сортировка. С помощью алгоритма поиска можно использовать квазислучайные числа для нахождения режима, медианы, доверительных интервалов и совокупного распределения статистического распределения, а также всех локальных минимумов и всех решений детерминированных функций.

Последовательности с низким расхождением при численном интегрировании

По крайней мере, три метода численного интегрирования можно сформулировать следующим образом. Учитывая набор { x 1,..., x N } в интервале [0,1], аппроксимируйте интеграл функции f как среднее значение функции, вычисленной в этих точках:

${\ displaystyle \ int _ {0} ^ {1} f (u) \, du \ приблизительно {\ frac {1} {N}} \, \ sum _ {i = 1} ^ {N} f (x_ { я}).}$

Если точки выбраны как x i = i / N, это правило прямоугольника. Если точки выбраны для случайного (или псевдослучайного ) распределения, это метод Монте-Карло. Если точки выбраны как элементы последовательности с низким расхождением, это квази-Монте-Карло метод. Замечательный результат, неравенство Коксмы – Главки (изложенное ниже), показывает, что погрешность такого метода может быть ограничена произведением двух членов, одно из которых зависит только от f, а другое - невязка множества { x 1,..., x N }.

Множество { x 1,..., x N } удобно построить таким образом, чтобы при построении набора из N +1 элементов не нужно было пересчитывать предыдущие N элементов. Правило прямоугольника использует набор точек с низким расхождением, но в целом элементы должны быть пересчитаны, если N увеличивается. Элементы не нужно пересчитывать в случайном методе Монте-Карло, если N увеличивается, но наборы точек не имеют минимального расхождения. Используя последовательности с низким несоответствием, мы стремимся к низкому несоответствию и отсутствию необходимости в повторных вычислениях, но на самом деле последовательности с низким несоответствием могут быть постепенно улучшены при несоответствии, если мы не допускаем повторного вычисления.

Несоответствие из множества Р = { х 1,..., х N } определяется, используя Нидеррейтер в обозначение, как и

${\ Displaystyle D_ {N} (P) = \ sup _ {B \ in J} \ left | {\ frac {A (B; P)} {N}} - \ lambda _ {s} (B) \ right |}$

где λ s - s -мерная мера Лебега, A ( B ; P) - количество точек в P, попадающих в B, а J - множество s -мерных интервалов или ящиков вида

${\ displaystyle \ prod _ {i = 1} ^ {s} [a_ {i}, b_ {i}) = \ {\ mathbf {x} \ in \ mathbf {R} ^ {s}: a_ {i} \ leq x_ {i} lt;b_ {i} \} \,}$

где. ${\ displaystyle 0 \ leq a_ {i} lt;b_ {i} \ leq 1}$

Звезда несоответствие Д ^*Н ( Р) определяется аналогично, за исключением того, что верхняя грань берется по множеству J ^* прямоугольных коробок вида

${\ Displaystyle \ prod _ {я = 1} ^ {s} [0, и_ {я})}$

где u i находится в полуоткрытом интервале [0, 1).

Эти двое связаны между собой

${\ Displaystyle D_ {N} ^ {*} \ leq D_ {N} \ leq 2 ^ {s} D_ {N} ^ {*}. \,}$

Примечание: с этими определениями несоответствие представляет собой наихудшее или максимальное отклонение плотности точек однородного набора. Однако значимы и другие меры погрешности, ведущие к другим определениям и мерам вариации. Например, L2-несоответствие или модифицированное центрированное L2-несоответствие также интенсивно используются для сравнения качества однородных наборов точек. И то, и другое намного проще вычислить для больших N и s.

Пусть Ī ^s - s -мерный единичный куб, Ī ^s = [0, 1] ×... × [0, 1]. Пусть f имеет ограниченную вариацию V ( f) на ^s в смысле Харди и Краузе. Тогда для любых x 1,..., x N в I ^s = [0, 1) ×... × [0, 1),

${\ displaystyle \ left | {\ frac {1} {N}} \ sum _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s }} f (u) \, du \ right | \ leq V (f) \, D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}).}$

Коксма - Hlawka неравенство является точным в следующем смысле: для любой точки множества { х 1,..., х N } в Я ^ей и любой, существует функция F с ограниченной вариации и V ( ф) = 1 такой, что ${\ displaystyle \ varepsilongt; 0}$

${\ displaystyle \ left | {\ frac {1} {N}} \ sum _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s }} f (u) \, du \ right |gt; D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) - \ varepsilon.}$

Следовательно, качество правила численного интегрирования зависит только от расхождения D ^*N ( x 1,..., x N).

Пусть. Для нас пишут ${\ Displaystyle D = \ {1,2, \ ldots, d \}}$${\ Displaystyle \ emptyset \ neq и \ substeq D}$

${\ displaystyle dx_ {u}: = \ prod _ {j \ in u} dx_ {j}}$

и обозначим точкой, полученной из x заменой координат, не входящих в u, на. потом ${\ displaystyle (x_ {u}, 1)}$${\ displaystyle 1}$

${\ displaystyle {\ frac {1} {N}} \ sum _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s}} f (u) \, du = \ sum _ {\ emptyset \ neq u \ substeq D} (- 1) ^ {| u |} \ int _ {[0,1] ^ {| u |}} \ operatorname {disk } (x_ {u}, 1) {\ frac {\ partial ^ {| u |}} {\ partial x_ {u}}} f (x_ {u}, 1) \, dx_ {u},}$

где - функция невязки. ${\ displaystyle \ operatorname {disc} (z) = {\ frac {1} {N}} \ sum _ {i = 1} ^ {N} \ prod _ {j = 1} ^ {d} 1 _ {[0, z_ {j})} (x_ {i, j}) - \ prod _ {j = 1} ^ {d} z_ {i}}$

Применяя неравенство Коши – Шварца для интегралов и сумм к тождеству Главки – Зарембы, получаем версию неравенства Коксмы – Главки: ${\ displaystyle L ^ {2}}$

${\ displaystyle \ left | {\ frac {1} {N}} \ sum _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s }} f (u) \, du \ right | \ leq \ | f \ | _ {d} \ operatorname {disc} _ {d} (\ {t_ {i} \}),}$

где

${\ displaystyle \ operatorname {disc} _ {d} (\ {t_ {i} \}) = \ left (\ sum _ {\ emptyset \ neq u \ substeq D} \ int _ {[0,1] ^ { | u |}} \ operatorname {disc} (x_ {u}, 1) ^ {2} \, dx_ {u} \ right) ^ {1/2}}$

а также

${\ Displaystyle \ | е \ | _ {d} = \ left (\ sum _ {u \ substeq D} \ int _ {[0,1] ^ {| u |}} \ left | {\ frac {\ partial ^ {| u |}} {\ partial x_ {u}}} f (x_ {u}, 1) \ right | ^ {2} dx_ {u} \ right) ^ {1/2}.}$

Расхождение L2 имеет большое практическое значение, поскольку для данного набора точек возможны быстрые явные вычисления. Таким образом, легко создавать оптимизаторы набора точек, используя в качестве критериев несоответствие L2.

Вычислительно сложно найти точное значение невязки больших наборов точек. Erdős - Туран - Коксм неравенство дает верхнюю границу.

Пусть x 1,..., x N - точки в I ^s, а H - произвольное положительное целое число. потом

${\ displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ leq \ left ({\ frac {3} {2}} \ right) ^ {s} \ left ( {\ frac {2} {H + 1}} + \ sum _ {0 lt;\ | h \ | _ {\ infty} \ leq H} {\ frac {1} {r (h)}} \ left | { \ frac {1} {N}} \ sum _ {n = 1} ^ {N} e ^ {2 \ pi i \ langle h, x_ {n} \ rangle} \ right | \ right)}$

где

${\ displaystyle r (h) = \ prod _ {i = 1} ^ {s} \ max \ {1, | h_ {i} | \} \ quad {\ t_dv {for}} \ quad h = (h_ { 1}, \ ldots, h_ {s}) \ in \ mathbb {Z} ^ {s}.}$

Гипотеза 1. Существует постоянная c s, зависящая только от размерности s, такая, что

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq c_ {s} {\ frac {(\ ln N) ^ {s-1}} {N} }}$

для любого конечного точечного множества { x 1,..., x N }.

Гипотеза 2. Существует константа с ^'S, зависящим только от х, такой, что

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq c '_ {s} {\ frac {(\ ln N) ^ {s}} {N} }}$

для бесконечного числа N для любой бесконечной последовательности x 1, x 2, x 3,....

Эти предположения эквивалентны. Они были доказаны для s ≤ 2 В. М. Шмидтом. В более высоких измерениях соответствующая проблема все еще остается открытой. Наиболее известные нижние оценки получены Майклом Лейси и соавторами.

Пусть s  = 1. Тогда

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq {\ frac {1} {2N}}}$

для любого конечного точечного множества { x 1,...,  x N }.

Пусть s  = 2. В. М. Шмидт доказал, что для любого конечного точечного множества { x 1,...,  x N },

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq C {\ frac {\ log N} {N}}}$

где

${\ displaystyle C = \ max _ {a \ geq 3} {\ frac {1} {16}} {\ frac {a-2} {a \ log a}} = 0,023335 \ точек.}$

К.Ф. Рот для произвольных размерностей s  gt; 1 доказал, что

${\ displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq {\ frac {1} {2 ^ {4s}}} {\ frac {1} {(( s-1) \ log 2) ^ {\ frac {s-1} {2}}}} {\ frac {\ log ^ {\ frac {s-1} {2}} N} {N}}}$

для любого конечного точечного множества { x 1,...,  x N }. Йозеф Бек добился двукратного улучшения этого результата в трех измерениях. Это было улучшено Д. Билыком и М. Т. Лейси до степени единственного логарифма. Наиболее известная оценка для s  gt; 2 принадлежит Д. Билыку, М. Т. Лейси и А. Вагаршакяну. Для s  gt; 2 существует t  gt; 0, так что

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq t {\ frac {\ log ^ {{\ frac {s-1} {2}} + t } N} {N}}}$

для любого конечного точечного множества { x 1,...,  x N }.

Поскольку любое распределение случайных чисел может быть отображено в однородное распределение, а квазислучайные числа отображаются таким же образом, эта статья касается только генерации квазислучайных чисел в многомерном равномерном распределении.

Известны конструкции последовательностей такие, что

${\ displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ leq C {\ frac {(\ ln N) ^ {s}} {N}}.}$

где C - некоторая постоянная, зависящая от последовательности. После гипотезы 2 считается, что эти последовательности имеют наилучший порядок сходимости. Примеры ниже являются ван - дер - последовательности Корпута, в последовательности Halton, и последовательностей Соболь. Одним из общих ограничений является то, что методы построения обычно могут гарантировать только порядок сходимости. На практике низкое расхождение может быть достигнуто только в том случае, если N достаточно велико, а при большом заданном s этот минимум N может быть очень большим. Это означает, что выполнение анализа Монте-Карло, например, с s = 20 переменными и N = 1000 точками из генератора последовательности с низким расхождением, может дать лишь очень незначительное улучшение точности.

Случайные числа

Последовательности квазислучайных чисел могут быть сгенерированы из случайных чисел путем наложения отрицательной корреляции на эти случайные числа. Один из способов сделать это, чтобы начать с набором случайных чисел на и числах конструкта квазислучайных, равномерные на использовании: ${\ displaystyle r_ {i}}$${\ displaystyle [0,0.5)}$${\ displaystyle s_ {i}}$${\ displaystyle [0,1)}$

${\ displaystyle s_ {i} = r_ {i}}$для нечетных и для четных. ${\ displaystyle i}$${\ displaystyle s_ {i} = 0,5 + r_ {i}}$${\ displaystyle i}$

Второй способ сделать это с начальными случайными числами - построить случайное блуждание со смещением 0,5, как в:

${\ displaystyle s_ {i} = s_ {i-1} + 0,5 + r_ {i} {\ pmod {1}}. \,}$

То есть возьмите предыдущее квазислучайное число, сложите 0,5 и случайное число и возьмите результат по модулю  1.

Для более чем одного измерения можно использовать латинские квадраты соответствующего измерения для обеспечения смещения, чтобы гарантировать равномерное покрытие всей области.

Покрытие единицы кв. Слева для аддитивных квазислучайных чисел с c  = 0,5545497..., 0,308517... Справа для случайных чисел. Сверху донизу. 10, 100, 1000, 10000 очков.

Аддитивное повторение

Для любого иррационального последовательность ${\ displaystyle \ alpha}$

${\ Displaystyle s_ {п} = \ {s_ {0} + п \ альфа \}}$

имеет тенденцию к несоответствию. Обратите внимание, что последовательность может быть определена рекурсивно с помощью ${\ displaystyle 1 / N}$

${\ displaystyle s_ {n + 1} = (s_ {n} + \ alpha) {\ bmod {\,}} 1 \ ;.}$

Хорошее значение дает меньшее расхождение, чем последовательность независимых однородных случайных чисел. ${\ displaystyle \ alpha}$

Несоответствие может быть ограничена аппроксимации экспоненты в. Если показатель аппроксимации равен, то для любого имеет место следующая оценка: ${\ displaystyle \ alpha}$${\ displaystyle \ mu}$${\ displaystyle \ varepsilongt; 0}$

${\ Displaystyle D_ {N} ((s_ {n})) = O _ {\ varepsilon} (N ^ {- 1 / (\ mu -1) + \ varepsilon}).}$

По теореме Туэ – Зигеля – Рота показатель приближения любого иррационального алгебраического числа равен 2, что дает оценку выше. ${\ displaystyle N ^ {- 1+ \ varepsilon}}$

Приведенное выше рекуррентное отношение аналогично рекуррентному отношению, используемому линейным конгруэнтным генератором, генератором псевдослучайных чисел низкого качества:

${\ displaystyle r_ {i} = (ar_ {i-1} + c) {\ bmod {m}}}$

Для описанной выше аддитивной повторяемости с низким расхождением a и m выбраны равными 1. Обратите внимание, однако, что это не будет генерировать независимых случайных чисел, поэтому не должно использоваться для целей, требующих независимости.

Значение с наименьшим расхождением равно ${\ displaystyle c}$

${\ displaystyle c = {\ frac {{\ sqrt {5}} - 1} {2}} \ приблизительно 0,618034.}$

Еще одно значение, которое почти так же хорошо, это:

${\ displaystyle c = {\ sqrt {2}} - 1 \ приблизительно 0,414214. \,}$

В более чем одном измерении для каждого измерения необходимы отдельные квазислучайные числа. Удобный набор используемых значений - это квадратные корни из простых чисел от двух вверх, взятые по модулю 1:

${\ displaystyle c = {\ sqrt {2}}, {\ sqrt {3}}, {\ sqrt {5}}, {\ sqrt {7}}, {\ sqrt {11}}, \ ldots \,}$

Однако было показано, что набор значений, основанный на обобщенном золотом сечении, дает более равномерно распределенные точки.

В списке генераторов псевдослучайных чисел перечислены методы генерации независимых псевдослучайных чисел. Примечание. В некоторых измерениях рекурсивное повторение приводит к однородным наборам хорошего качества, но для больших s (например, sgt; 8) другие генераторы наборов точек могут предложить гораздо меньшие расхождения.

последовательность ван дер Корпута

Основная статья: последовательность ван дер Корпута

Позволять

${\ Displaystyle п = \ сумма _ {к = 0} ^ {L-1} d_ {к} (п) Ь ^ {к}}$

- b -арное представление натурального числа n ≥ 1, т. е. 0 ≤ d k ( n) lt; b. Набор

${\ displaystyle g_ {b} (n) = \ sum _ {k = 0} ^ {L-1} d_ {k} (n) b ^ {- k-1}.}$

Тогда существует постоянная C, зависящая только от b такая, что ( g b ( n)) n ≥ 1 удовлетворяет

${\ displaystyle D_ {N} ^ {*} (g_ {b} (1), \ dots, g_ {b} (N)) \ leq C {\ frac {\ log N} {N}},}$

где D ^*N - звездная невязка.

Последовательность Холтона

Первые 256 точек (2,3) последовательности Халтона Основная статья: последовательность Холтона

Последовательность Халтона является естественным обобщением последовательности Ван дер Корпута на более высокие измерения. Пусть s - произвольная размерность, а b 1,..., b s - произвольные взаимно простые целые числа больше 1. Определим

${\ displaystyle x (n) = (g_ {b_ {1}} (n), \ dots, g_ {b_ {s}} (n)).}$

Тогда существует константа C, зависящая только от b 1,..., b s, такая, что последовательность { x ( n)} n ≥1 является s -мерной последовательностью с

${\ displaystyle D_ {N} ^ {*} (x (1), \ dots, x (N)) \ leq C '{\ frac {(\ log N) ^ {s}} {N}}.}$

Набор Хаммерсли

2D набор Хаммерсли размера 256

Пусть Ь 1,..., б ы -1 быть взаимно простым целыми положительными числами больше 1. При заданной ей и N, то ев - мерном Хаммерл набор размера N определяется путем

${\ displaystyle x (n) = (g_ {b_ {1}} (n), \ dots, g_ {b_ {s-1}} (n), {\ frac {n} {N}})}$

для п = 1,..., N. потом

${\ Displaystyle D_ {N} ^ {*} (х (1), \ точки, х (N)) \ leq C {\ frac {(\ log N) ^ {s-1}} {N}}}$

где C - постоянная, зависящая только от b 1,..., b s −1. Примечание: формулы показывают, что множество Хаммерсли на самом деле является последовательностью Халтона, но мы бесплатно получаем еще одно измерение, добавляя линейную развертку. Это возможно только в том случае, если заранее известно N. Линейное множество - это также множество с минимально возможным одномерным несоответствием в целом. К сожалению, для более высоких измерений такие «наборы записей несоответствия» не известны. Для s  = 2 большинство генераторов наборов точек с малым расхождением выдают расхождения, по крайней мере, почти оптимальные.

Последовательность Соболя

Основная статья: Последовательность Соболя

Вариант Антонова – Салеева последовательности Соболя генерирует числа от нуля до единицы непосредственно как двоичные дроби длины из набора специальных двоичных дробей, называемых числами направления. Биты кода Грея из,, используются для выбора номера направления. Чтобы получить значение последовательности Соболя, возьмите исключающее ИЛИ двоичного значения кода Грея с соответствующим номером направления. Количество требуемых размеров влияет на выбор. ${\ displaystyle w}$${\ displaystyle w}$${\ Displaystyle V_ {я}, я = 1,2, \ точки, ш}$ ${\ displaystyle i}$${\ Displaystyle G (я)}$${\ displaystyle s_ {i}}$ ${\ displaystyle i}$${\ displaystyle V_ {i}}$

Выборка диска Пуассона

Основная статья: суперсэмплинг § диск Пуассона

Выборка диска Пуассона популярна в видеоиграх для быстрого размещения объектов так, чтобы они выглядели случайными, но гарантируют, что каждые две точки разделены по крайней мере на указанное минимальное расстояние. Это не гарантирует низкого расхождения (как, например, Соболь), но по крайней мере значительно меньшее расхождение, чем чистая случайная выборка. Цель этих шаблонов выборки основана на частотном анализе, а не на несоответствии, типе так называемых шаблонов «синего шума».

Точки, нанесенные ниже, - это первые 100, 1000 и 10000 элементов последовательности типа Соболь. Для сравнения также показаны 10000 элементов последовательности псевдослучайных точек. Последовательность с низким расхождением была сгенерирована алгоритмом 659 TOMS. Реализация алгоритма на Фортране доступна в Netlib.

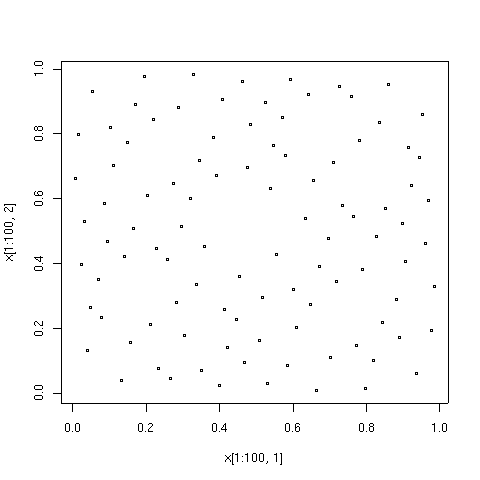Первые 100 точек в последовательности с малым расхождением типа Соболя. 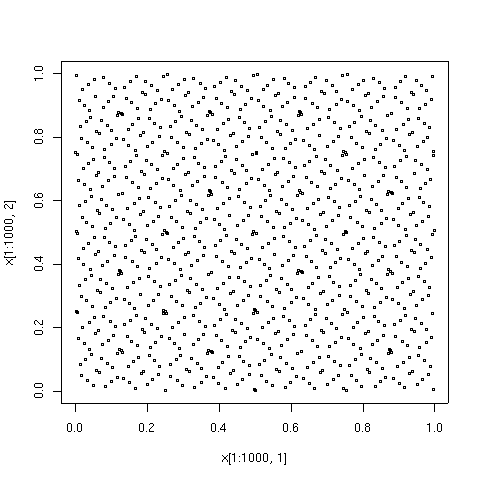Первые 1000 точек в той же последовательности. Эти 1000 составляют первые 100 с еще 900 очками. 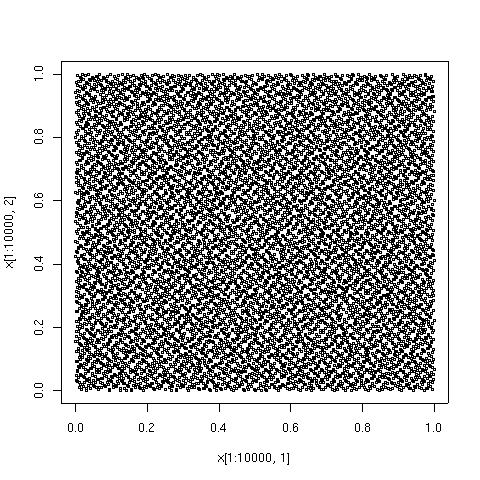Первые 10000 точек в той же последовательности. Эти 10000 составляют первую 1000 с еще 9000 очками. 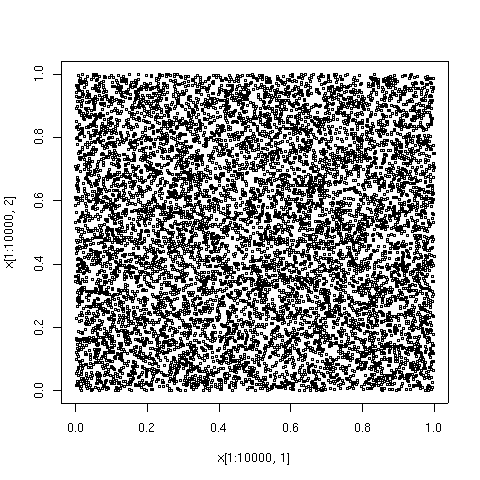Для сравнения - первые 10000 точек в последовательности равномерно распределенных псевдослучайных чисел. Очевидны области большей и меньшей плотности.

• Теория несоответствия
• Цепь Маркова Монте-Карло
• Квази-Монте-Карло метод
• Разреженная сетка

• Йозеф Дик и Фридрих Пиллихсхаммер, Цифровые сети и последовательности. Теория несоответствия и интеграция квази-Монте-Карло, Cambridge University Press, Кембридж, 2010, ISBN   978-0-521-19159-3
• Kuipers, L.; Нидеррейтер, Х. (2005), Равномерное распределение последовательностей, Dover Publications, ISBN   0-486-45019-8
• Харальд Нидеррайтер. Генерация случайных чисел и методы квази-Монте-Карло. Общество промышленной и прикладной математики, 1992. ISBN   0-89871-295-5
• Майкл Дрмота и Роберт Ф. Тихи, Последовательности, несоответствия и приложения, Лекционные заметки по математике., 1651, Springer, Berlin, 1997, ISBN   3-540-62606-9
• Уильям Х. Пресс, Брайан П. Фланнери, Сол А. Теукольски, Уильям Т. Веттерлинг. Численные Рецепты в C. Кембридж, Великобритания: Издательство Кембриджского университета, второе издание, 1992 г. ISBN   0-521-43108-5 (см. Раздел 7.7 для менее технического обсуждения последовательностей с низким расхождением)

• Собранные алгоритмы ACM (см. Алгоритмы 647, 659 и 738.)
• Квазислучайные последовательности из научной библиотеки GNU
• Квазислучайная выборка с ограничениями на FinancialMat Mathematics.Com
• C ++ генератор последовательности Соболя