Поворот Дена

редактировать

Положительный поворот Дена, примененный к цилиндру вокруг красной кривой c, изменяет зеленая кривая, как показано.

В геометрической топологии, ветви математики, поворот Дена представляет собой определенный тип самогомеоморфизма поверхности поверхности (двумерное многообразие ).

Содержание

1 Определение
2 Пример
3 Группа классов отображения
4 См. Также
5 Ссылки

Определение

Общее скручивание Дена на компактной поверхности, представленное буквой n -gon.

Предположим, что c - простая замкнутая кривая на замкнутой ориентируемой поверхности S. Пусть A - трубчатая окрестность точки c. Тогда A является кольцом, гомеоморфным декартову произведению окружности и единичного интервала I:

c ⊂ A ≅ S 1 × I. {\ displaystyle c \ subset A \ cong S ^ {1} \ times I.}

{\ displaystyle c \ subset A \ cong S ^ {1} \ times I.}

Дайте координаты A (s, t), где s - комплексное число в форме $ei θ {\ displaystyle e ^ { я \ theta}}$ $e ^ {я \ theta}$ с $θ ∈ [0, 2 π], {\ displaystyle \ theta \ in [0,2 \ pi],}$ ${\ displaystyle \ theta \ in [0,2 \ pi],}$ и t ∈ [ 0, 1].

Пусть f будет отображением S в себя, которое является тождеством вне A, а внутри A мы имеем

f (s, t) = (s e i 2 π t, t). {\ displaystyle f (s, t) = \ left (se ^ {i2 \ pi t}, t \ right).}

{\ displaystyle f (s, t) = \ left (se ^ {i2 \ pi t}, t \ right).}

Тогда f является поворотом Дена вокруг кривой c.

Скручивания Дена также могут быть определены на неориентируемой поверхности S, при условии, что они начинаются с двусторонней простой замкнутой кривой c на S.

Пример

Пример скручивания Дена на торе вдоль замкнутой кривой a, выделенной синим цветом, где a - ребро фундаментального многоугольника, представляющего тор.

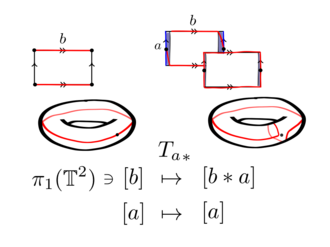
Автоморфизм на фундаментальной группе тора, индуцированный самовоспроизведением. гомеоморфизм скручивания Дена вдоль одного из образующих тора.

Рассмотрим тор, представленный фундаментальным многоугольником с ребрами a и b

T 2 ≅ R 2 / Z 2. {\ displaystyle \ mathbb {T} ^ {2} \ cong \ mathbb {R} ^ {2} / \ mathbb {Z} ^ {2}.}

{\ displaystyle \ mathbb {T} ^ {2} \ cong \ mathbb {R} ^ {2} / \ mathbb {Z} ^ {2}.}

Пусть замкнутая кривая будет линией вдоль края a, называемого $γ a {\ displaystyle \ gamma _ {a}}$ $\ gamma_a$ .

Учитывая выбор склейки гомеоморфизма на рисунке, трубчатая окрестность кривой $γ a {\ displaystyle \ gamma _ {a}}$ $\ gamma_a$ будет выглядеть как обвязка, обвязанная вокруг пончика. Эта окрестность гомеоморфна кольцу, скажем,

a (0; 0, 1) = {z ∈ C: 0 < | z | < 1 } {\displaystyle a(0;0,1)=\{z\in \mathbb {C} :0<|z|<1\}}

{\ displaystyle a (0; 0,1) = \ {z \ in \ mathbb {C}: 0 <| z | <1 \}}

на комплексной плоскости.

Путем продолжения на тор скручивающее отображение $(ei θ, t) ↦ (ei (θ + 2 π t), t) {\ displaystyle \ left (e ^ {i \ theta}, t \ right) \ mapsto \ left (e ^ {i \ left (\ theta +2 \ pi t \ right)}, t \ right)}$ ${\ Displaystyle \ влево (е ^ {я \ тета}, т \ вправо) \ mapsto \ влево (е ^ {я \ влево (\ тета +2 \ пи т \ вправо)}, т \ вправо)}$ кольца через гомеоморфизмы кольца к открытый цилиндр в окрестности $γ a {\ displaystyle \ gamma _ {a}}$ $\ gamma_a$ , дает скручивание тора Дена на a.

T a: T 2 → T 2 {\ displaystyle T_ {a}: \ mathbb {T} ^ {2} \ to \ mathbb {T} ^ {2}}

{\ displaystyle T_ {a}: \ mathbb {T} ^ {2} \ to \ mathbb {T} ^ {2}}

Этот собственный гомеоморфизм действует на замкнутом кривая по б. В трубчатой окрестности он проходит кривую b один раз вдоль кривой a.

Гомеоморфизм между топологическими пространствами индуцирует естественный изоморфизм между их фундаментальными группами. Следовательно, имеется автоморфизм

T a ∗: π 1 (T 2) → π 1 (T 2): [x] ↦ [T a (x)] {\ displaystyle {T_ {a}} _ {\ ast }: \ pi _ {1} \ left (\ mathbb {T} ^ {2} \ right) \ to \ pi _ {1} \ left (\ mathbb {T} ^ {2} \ right): [x] \ mapsto \ left [T_ {a} (x) \ right]}

{\ displaystyle {T_ {a}} _ {\ ast}: \ pi _ {1} \ left (\ mathbb {T} ^ {2} \ right) \ to \ pi _ {1} \ left (\ mathbb {T} ^ {2} \ right): [x] \ mapsto \ left [T_ {a} (x) \ right]}

где [x] - гомотопические классы замкнутой кривой x в торе. Обратите внимание: $T a ∗ ([a]) = [a] {\ displaystyle {T_ {a}} _ {\ ast} ([a]) = [a]}$ ${T_a} _ \ ast ([a]) = [a]$ и $T a * ([b]) = [b * a] {\ displaystyle {T_ {a}} _ {\ ast} ([b]) = [b * a]}$ ${\ displaystyle {T_ {a}} _ {\ ast} ([b]) = [b * a]}$ , где $b ∗ a {\ displaystyle b * a}$ $б * a$ - это путь, пройденный вокруг точки b, затем a.

Группа классов отображения

Кривые 3g - 1 из теоремы о скручивании, показанные здесь для g = 3.

Теорема Макса Дена отображает эту форму генерировать группу классов отображения из изотопических классов сохраняющих ориентацию гомеоморфизмов любого замкнутого, ориентированного рода - $g {\ displaystyle g}$ $g$ поверхность. В. Б. Р. Ликориш позже переоткрыл этот результат с помощью более простого доказательства и, кроме того, показал, что Ден скручивает по $3 g - 1 {\ displaystyle 3g-1}$ ${\ displaystyle 3g-1}$ явные кривые, генерирующие группу классов отображения (это называется каламбурным названием «Лизкоришная теорема о твисте»); это число было позже улучшено до $2 g + 1 {\ displaystyle 2g + 1}$ $2g + 1$ для $g>1 {\ displaystyle g>1}$ $g>1$ , которое, как он показал, было минимальным числом. 120>

Ликориш также получил аналогичный результат для неориентируемых поверхностей, которые требуют не только скручивания Дена, но и «Y-гомеоморфизмов.»

См. Также

Фонарь отношение

Ссылки

Эндрю Дж. Кассон, Стивен А. Блейлер, Автоморфизмы поверхностей по Нильсену и Терстону, Cambridge University Press, 1988. ISBN 0-521-34985-0.
Стивен П. Хамфрис, «Генераторы для группы классов отображений», в: Топология многообразий низкой размерности (Proc. Second Sussex Conf., Chelwood Gate, 1977), стр. 44– 47, Lecture Notes in Math., 722, Springer, Berlin, 1979. MR 0547453
WBR Lickorish, "Представление ориентируемых комбинаторные 3-многообразия. Ann. математики. (2) 76 1962 531—540. MR 0151948
W. Б. Р. Ликориш, "Конечный набор образующих для гомотопической группы двумерного многообразия", Proc. Cambridge Philos. Soc. 60 (1964), 769–778. MR 0171269