Войти
В математике, константный пучок на топологическом пространстве X, связанный с набором A - это пучок множеств на X, все стебли которого равны A. Он обозначается A или A X. Константа предварительный пучок со значением A - это предварительный пучок, который присваивает каждому непустому открытому подмножеству X значение A, и все карты ограничений которого являются тождественное отображение A → A. Постоянный пучок, связанный с A, является связкой постоянного предварительного пучка, связанного с A.
В некоторых случаях набор A может быть заменен на объект A в некоторой категории C(например, когда C является категорией абелевых групп или коммутативных колец ).
Постоянные пучки абелевых групп появляются, в частности, как коэффициенты в когомологии пучков.
Пусть X - топологическое пространство, а A - множество. Сечения постоянного пучка A над открытым множеством U можно интерпретировать как непрерывные функции U → A, где A задана дискретная топология . Если U подключен, то эти локально постоянные функции постоянны. Если f: X → {pt} - это уникальное отображение в одноточечное пространство и A рассматривается как пучок на {pt}, то обратное изображение fA - это константа пучок A на X. Пространство пучков кольца A - это отображение проекции X × A → X (где A задана дискретная топология).
Постоянный предпучок на двухточечном дискретном пространстве 
Двухточечное дискретное топологическое пространство Пусть X будет топологическим пространством, состоящим из двух точек p и q с дискретная топология. X имеет четыре открытых множества: ∅, {p}, {q}, {p, q}. Пять нетривиальных включений открытых множеств X показаны на диаграмме.
Предварительный пучок на X выбирает набор для каждого из четырех открытых наборов X и карту ограничений для каждого из девяти включений (пять нетривиальных включений и четыре тривиальных). Константа предварительный пучок со значением Z, который мы обозначим как F, является предварительным пучком, который выбирает все четыре набора как Z, целые числа и все ограничительные карты. быть личностью. F - функтор, следовательно, предпучок, поскольку он постоянен. F удовлетворяет аксиоме склейки, но это не пучок, потому что он не удовлетворяет аксиоме локального тождества на пустом множестве. Это связано с тем, что пустое множество покрывается пустым семейством множеств: Вакуумно любые две секции F над пустым множеством равны, если ограничены любым множеством в пустом семействе. Таким образом, из аксиомы локального тождества следует, что любые две секции F на пустом множестве равны, но это неверно.
Аналогичный предпучок G, удовлетворяющий аксиоме локального тождества над пустым множеством, строится следующим образом. Пусть G (∅) = 0, где 0 - одноэлементное множество. На всех непустых наборах присвойте G значение Z . Для каждого включения открытых множеств G возвращает либо уникальную карту в 0, если меньший набор пуст, либо карту идентичности на Z.
Промежуточный шаг для постоянного пучка Обратите внимание, что как следствие аксиомы локальной идентичности для пустого множества все карты ограничений, включающие пустое множество, утомительны. Это верно для любого предпучка, удовлетворяющего аксиоме локальной идентичности для пустого множества, и, в частности, для любого пучка.
G является отделенным предпучком (то есть удовлетворяет аксиоме локального тождества), но, в отличие от F, не удовлетворяет аксиоме склейки. {p, q} покрывается двумя открытыми наборами {p} и {q}, и эти множества имеют пустое пересечение. Раздел на {p} или на {q} является элементом Z, то есть это число. Выберите сечение m над {p} и n над {q} и предположите, что m ≠ n. Поскольку m и n ограничиваются одним и тем же элементом 0 над ∅, аксиома склейки требует существования единственного сечения s на G ({p, q}), которое ограничивается до m на {p} и n на {q}. Но поскольку отображение ограничения из {p, q} в {p} является тождественным, s = m, и аналогично s = n, поэтому m = n, противоречие.
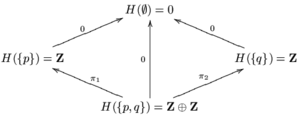Постоянный пучок в двухточечном топологическом пространстве G ({p, q}) слишком мал, чтобы нести информацию как о {p}, так и о {q}. Чтобы увеличить его так, чтобы он удовлетворял аксиоме склейки, пусть H ({p, q}) = Z⊕ Z. Пусть π 1 и π 2 - две карты проекции Z⊕ Z→ Z. Определите H ({p}) = im (π 1) = Z и H ({q}) = im (π 2) = Z . Для остальных открытых множеств и включений пусть H равно G. H - пучок, называемый постоянным пучком на X со значением Z . Поскольку Z - кольцо, а все отображения ограничения - гомоморфизмы колец, H - пучок коммутативных колец.
