Каталонское число

редактировать

Рекурсивная целочисленная последовательность

C 5 = 42 непересекающиеся разделы Набор из 5 элементов (ниже, другие 10 разделов 52 )

В комбинаторной математике, каталонские числа образуют последовательность из натуральные числа, которые встречаются в различных задачах подсчета, часто с рекурсивно определенными объектами. Они названы в честь бельгийского математика Эжена Шарля Каталана (1814–1814). 1894).

n-е каталонское число дается непосредственно через биномиальные коэффициенты как

C n = 1 n + 1 (2 nn) = (2 n)! (N + 1)! N! = ∏ К = 2 nn + kk для n ≥ 0. {\ displaystyle C_ {n} = {\ frac {1} {n + 1}} {2n \ choose n} = {\ frac { (2n)!} {(N + 1)! \, N!}} = \ Prod \ limits _ {k = 2} ^ {n} {\ frac {n + k} {k}} \ qquad {\ text {for}} n \ geq 0.}

C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}=\prod \limits _{k=2}^{n}{\frac {n+k}{k}}\qquad {\text{for }}n\geq 0.

Первые каталонские числа для n = 0, 1, 2, 3,...:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452,... (последовательность A000>в составе 359>1 Свойства

2 Приложения в комбинаторике

3 Доказательство формулы

3.1 Первое доказательство
3.2 Второе доказательство
3.3 Третье доказательство
3.4 Четвертое доказательство
3.5 Пятое доказательство
3.6 Шестое доказательство

4 Матрица Ганкеля

5 История

6 Обобщения

7 См. Также

8 Примечания

9 Ссылки

10 Внешние ссылки

Свойства

Альтернативное выражение для C n -

C n = (2 nn) - (2 nn + 1) = 1 n + 1 (2 nn) для n ≥ 0, {\ displaystyle C_ {n} = {2n \ choose n} - {2n \ choose n + 1} = {1 \ over n + 1} {2n \ choose n} \ quad {\ text {for}} n \ geq 0,}

C_ {n} = {2n \ choose n} - {2n \ choose n + 1} = {1 \ over n + 1} {2n \ choose n} \ quad {\ текст {for}} n \ geq 0,

, что эквивалентно приведенному выше выражению, потому что $(2 nn + 1) = nn + 1 (2 nn) {\ displaystyle {\ tbinom {2n} {n + 1}} = {\ tfrac {n } {n + 1}} {\ tbinom {2n} {n}}}$ ${\ tbinom {2n} {n + 1}} = {\ tfrac {n} {n + 1}} {\ tbinom {2n } {n}}$ . Это показывает, что C n является целым числом, что не сразу очевидно из первой приведенной формулы. Это выражение составляет основу доказательства правильности формулы.

. Каталонские числа удовлетворяют рекуррентным соотношениям

C 0 = 1 и C n + 1 = ∑ i = 0 n C i C n - я для n ≥ 0, {\ displaystyle C_ {0} = 1 \ quad {\ text {and}} \ quad C_ {n + 1} = \ sum _ {i = 0} ^ {n} C_ { i} \, C_ {ni} \ quad {\ text {for}} n \ geq 0,}

C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_ {i}\,C_{ni}\quad {\text{for }}n \geq 0,

∑ i 1 + ⋯ + im = n, i 1,…, im ≥ 0 C i 1 ⋯ C im = {m (n + 1) (n + 2) ⋯ (n + m / 2 - 1) 2 (n + m / 2 + 2) (n + m / 2 + 3) ⋯ (n + m) C n + m / 2, m даже m (n + 1) (n + 2) ⋯ (n + (m - 1) / 2) (n + (m + 3) / 2) (n + (m + 3) / 2 + 1) ⋯ (N + m) C N + (m - 1) / 2, m нечетное, {\ displaystyle \ sum _ {i_ {1} + \ cdots + i_ {m} = n, i_ {1}, \ ldots, i_ {m} \ geq 0} C_ {i_ {1}} \ cdots C_ {i_ {m}} = {\ begin {cases} {\ dfrac {m (n + 1) (n + 2) \ cdots (n + m / 2-1)} {2 (n + m / 2 + 2) (n + m / 2 + 3) \ cdots (n + m)}} C_ {n + m / 2}, m {\ text {even}} \\ [5pt] {\ dfrac {m (n + 1) (n + 2) \ cdots (n + (m-1) / 2)} {(n + (m + 3) / 2) (n + (m + 3) / 2 + 1) \ cdots (n + m)}} C_ {n + (m-1) / 2}, m {\ text {odd,}} \ end {case}} }

\sum _{i_{1}+\cdots +i_{m}=n,i_{1},\ldots,i_{m}\geq 0}C_{i_{1}}\cdots C_{i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2)(n+m/2+3)\cdots (n+m)}}C_{n+m/2},m{\text{ even}}\\[5pt]{\dfrac {m(n+1)(n+2)\cdots (n+(m-1)/2)}{(n+(m+3)/2)(n+(m+3)/2+1)\cdots (n+m)}}C_{n+(m-1)/2},m{\text{ odd,}}\end{cases}}

C 0 = 1 и C n + 1 = 2 (2 n + 1) n + 2 C n. {\ displaystyle C_ {0} = 1 \ quad {\ text {and}} \ quad C_ {n + 1} = {\ frac {2 (2n + 1)} {n + 2}} C_ {n}.}

{\ displaystyle C_ {0} = 1 \ quad {\ text {and}} \ quad C_ {n + 1} = {\ frac {2 (2n + 1) } {n + 2}} C_ {n}.}

Асимптотически каталонские числа растут как

C n ∼ 4 nn 3/2 π {\ displaystyle C_ {n} \ sim {\ frac {4 ^ {n}} {n ^ {3/2} { \ sqrt {\ pi}}}}}

C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}

в том смысле, что частное n-го каталонского числа и выражения справа стремится к 1, когда n приближается к бесконечности. Это можно доказать с помощью приближения Стирлинга для n! или через производящие функции.

Нечетными являются только каталонские числа C n, для которых n = 2 - 1; все остальные равны. Единственными простыми каталонскими числами являются C 2 = 2 и C 3 = 5.

Каталонские числа имеют целочисленное представление

C n = ∫ 0 4 xn ρ (x) dx, {\ displaystyle C_ {n} = \ int _ {0} ^ {4} x ^ {n} \ rho (x) \, dx,}

C_{n}=\int _{0}^{4}x^{n}\rho (x)\,dx,

где $ρ (x) = 1 2 π 4 - хх. {\ displaystyle \ rho (x) = {\ tfrac {1} {2 \ pi}} {\ sqrt {\ tfrac {4-x} {x}}}.}$ $\ rho (x) = {\ tfrac {1} {2 \ pi}} {\ sqrt {\ tfrac {4-x} {x}}}.$ Это означает, что каталонский числа являются решением версии проблемы моментов Хаусдорфа.

Приложения в комбинаторике

В комбинаторике существует множество задач счета, решение которых дается каталонскими числами. Книга «Перечислительная комбинаторика: том 2» комбинаториста Ричарда П. Стэнли содержит набор упражнений, описывающих 66 различных интерпретаций каталонских чисел. Ниже приведены некоторые примеры с иллюстрациями случаев C 3 = 5 и C 4 = 14.

Решетка из 14 слов Дайка длины 8 - (и), интерпретируемых как вверх и вниз

Cn- это количество слов Дика длиной 2n. Слово Дика - это строка , состоящая из n X и n Y, так что ни один начальный сегмент строки не имеет больше Y, чем X. Например, следующие слова Дика длины 6:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.

Повторная интерпретация символа X как открытой круглой скобки и Y как закрывающей скобки, C n подсчитывает количество правильно сопоставленных выражений, содержащих n пар круглых скобок:

((())) () (()) () () () (()) () (() ())

Cn- это количество различных способов, которыми n + 1 факторов могут быть полностью заключены в скобки (или количество способов связать n приложений бинарного оператора ). Для n = 3, например, у нас есть следующие пять различных скобок для четырех факторов:

((ab) c) d (a (bc)) d (ab) (cd) a ((bc) d) a (b (cd))

ассоциаэдр порядка 4 с полными бинарными деревьями C 4 = 14 с 5 листьями

Последовательные применения бинарного оператора могут быть представлены в терминах полного двоичного дерева. (Бинарное дерево с корнем является полным, если каждая вершина имеет двух дочерних элементов или их нет.) Отсюда следует, что C n - это количество полных двоичных деревьев с n + 1 листьями:

двоичное дерево каталонских чисел example.png

Cn- количество неизоморфных упорядоченных (или плоских) деревьев с n + 1 вершинами.
Cn- количество монотонных путей решетки по краям сетки с n × n квадратных ячеек, которые не выходят за диагональ. Монотонный путь - это путь, который начинается в нижнем левом углу, заканчивается в верхнем правом углу и полностью состоит из ребер, направленных вправо или вверх. Подсчет таких путей эквивалентен подсчету слов Дика: X означает «двигаться вправо», а Y означает «двигаться вверх».

На следующих диаграммах показан случай n = 4:

Это можно кратко представить, перечислив Каталонские элементы по высоте столбца:

[0,0,0,0] [0,0,0,1] [0,0,0,2] [0,0,1,1] [0,1,1,1] [0,0,1,2] [0,0,0,3] [0,1,1,2] [0,0,2,2] [ 0,0,1,3] [0,0,2,3] [0,1,1,3] [0,1,2,2] [0,1,2,3]

Треугольники соответствуют внутренним узлам бинарных деревьев.

A выпуклый многоугольник с n + 2 сторонами можно разрезать на треугольники, соединив вершины непересекающимися отрезками линии (форма триангуляции многоугольника ). Количество образованных треугольников равно n, и количество различных способов, которыми это может быть достигнуто, равно C n. Следующие шестиугольники иллюстрируют случай n = 4:

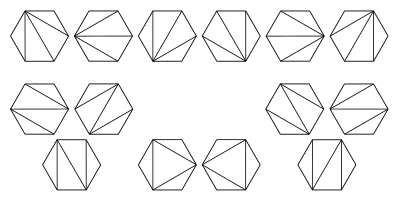
Cn- это количество стека -сортируемых перестановок из {1,..., n}. Перестановка w называется сортируемой по стеку, если S (w) = (1,..., n), где S (w) определяется рекурсивно следующим образом: напишите w = unv, где n - наибольшее элемент в w и u и v являются более короткими последовательностями и устанавливают S (w) = S (u) S (v) n, где S является тождеством для одноэлементных последовательностей.
Cn- количество перестановок {1,..., n}, которые избегают шаблона перестановки 123 (или, альтернативно, любого из других шаблонов длины 3); то есть количество перестановок без трехчленной возрастающей подпоследовательности. Для n = 3 эти перестановки равны 132, 213, 231, 312 и 321. Для n = 4 это 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312. и 4321.
Cn- количество непересекающихся разделов набора {1,..., n}. Тем более, C n никогда не превышает n-го Белл-числа. C n - это также количество непересекающихся разделов множества {1,..., 2n}, в котором каждый блок имеет размер 2. Соединение этих двух фактов может использоваться в доказательстве с помощью математическая индукция, что все свободные кумулянты степени больше 2 из закона полукруга Вигнера равны нулю. Этот закон важен в теории свободной вероятности, а теория случайных матриц.
Cn- это количество способов замостить ступеньку высотой n n прямоугольниками. На следующем рисунке показан случай n = 4:

Cn- это количество способов сформировать «горный хребет» с n ходами вверх и n ходами вниз, которые все остаются выше горизонтальной линии. Интерпретация горного хребта состоит в том, что горы никогда не уйдут за горизонт.

Cn- это число стандартных таблиц Юнга, диаграмма которых представляет собой прямоугольник 2 на n. Другими словами, это количество способов, которыми числа 1, 2,..., 2n могут быть расположены в прямоугольнике 2 на n так, чтобы каждая строка и каждый столбец увеличивались. Таким образом, формула может быть получена как частный случай формулы длины крюка ..
Cn- это количество способов, которыми вершины выпуклого 2n-угольника могут быть спарены так, чтобы отрезки линии, соединяющие парные вершины, делали не пересекаются. Это в точности условие, которое гарантирует, что парные ребра могут быть идентифицированы (сшиты вместе) для образования замкнутой поверхности нулевого рода (топологической двумерной сферы).
Cn- количество полупорядков на n немаркированные элементы.
В химической инженерии C n − 1 - это количество возможных последовательностей разделения, которые могут разделить смесь из n компонентов.

Доказательство формулы

Есть несколько способов объяснить, почему формула

C n = 1 n + 1 (2 nn) {\ displaystyle C_ {n} = {\ frac {1} {n + 1}} {2n \ choose n} }

C_{n}={\frac {1}{n+1}}{2n \choose n}

решает комбинаторные проблемы, перечисленные выше. В первом доказательстве ниже используется производящая функция . Остальные доказательства являются примерами биективных доказательств ; они включают в себя буквальный подсчет набора каких-то объектов, чтобы прийти к правильной формуле.

Первое доказательство

Сначала заметим, что все комбинаторные задачи, перечисленные выше, удовлетворяют рекуррентному соотношению Сегнера

C 0 = 1 и C n + 1 Знак равно ∑ я знак равно 0 N С я С N - я для N ≥ 0. {\ Displaystyle C_ {0} = 1 \ quad {\ text {и}} \ quad C_ {n + 1} = \ sum _ {i = 0} ^ {n} C_ {i} \, C_ {ni} \ quad {\ text {for}} n \ geq 0.}

C_ {0} = 1 \ quad {\ text {and}} \ quad C_ {n + 1} = \ sum _ {i = 0 } ^ {n} C_ {i} \, C_ {ni} \ quad {\ text {for}} n \ geq 0.

Например, каждое слово Дика w длины ≥ 2 может быть записано в уникальный способ в форме

w = Xw 1Yw2

с (возможно, пустыми) словами Дика w 1 и w 2.

Производящая функция для каталонских чисел определяется следующим образом:

c (x) = n = 0 ∞ C nxn. {\ displaystyle c (x) = \ sum _ {n = 0} ^ {\ infty} C_ {n} x ^ {n}.}

c(x)=\sum _{n=0}^{\infty }C_{n}x^{n}.

Рекуррентное соотношение, приведенное выше, можно затем резюмировать в форме производящей функции с помощью соотношение

c (x) = 1 + xc (x) 2; {\ displaystyle c (x) = 1 + xc (x) ^ {2};}

c(x)=1+xc(x)^{2};

другими словами, это уравнение следует из рекуррентного соотношения путем разложения обеих сторон в степенной ряд. С одной стороны, рекуррентное соотношение однозначно определяет каталонские числа; с другой стороны, соотношение производящей функции может быть решено алгебраически, давая

c (x) = 1 ∓ 1 - 4 x 2 x = 2 1 ± 1 - 4 x. {\ displaystyle c (x) = {\ frac {1 \ mp {\ sqrt {1-4x}}} {2x}} = {\ frac {2} {1 \ pm {\ sqrt {1-4x}}} }.}

{\ displaystyle c (x) = {\ frac {1 \ mp {\ sqrt {1-4x}}} {2x}} = {\ frac { 2} {1 \ pm {\ sqrt {1-4x}}}}.}

Если выбрать знак минус (в первом выражении), дробь будет иметь степенной ряд с номером 0, поэтому ее коэффициенты должны быть каталонскими числами. Это решение удовлетворяет условию

lim x → 0 + c (x) = C 0 = 1 {\ displaystyle \ lim _ {x \ to 0 ^ {+}} c (x) = C_ {0} = 1}

\lim _{x\to 0^{+}}c(x)=C_{0}=1

Другое решение со знаком плюс имеет полюс в 0, поэтому оно не может быть допустимым решением для c (x).

Член квадратного корня можно разложить в степенной ряд, используя тождество

1 + y = ∑ n = 0 ∞ (1 2 n) yn = ∑ n = 0 ∞ (- 1) n + 1 4 N (2 N - 1) (2 NN) YN знак равно 1 + 1 2 Y - 1 8 Y 2 + ⋯. {\ displaystyle {\ sqrt {1 + y}} = \ sum _ {n = 0} ^ {\ infty} {{\ frac {1} {2}} \ select n} y ^ {n} = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n + 1}} {4 ^ {n} (2n-1)}} {2n \ choose n} y ^ {n} = 1 + {\ frac {1} {2}} y - {\ frac {1} {8}} y ^ {2} + \ cdots.}

{\ displaystyle {\ sqrt {1 + y}} = \ sum _ {n = 0} ^ {\ infty } {{\ frac {1} {2}} \ choose n} y ^ {n} = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n + 1}} {4 ^ {n} (2n-1)}} {2n \ choose n} y ^ {n} = 1 + {\ frac {1} {2}} y - {\ frac {1} {8}} y ^ {2} + \ cdots.}

Это частный случай обобщенной биномиальной теоремы Ньютона. ; как и в случае с общей теоремой, это может быть доказано путем вычисления производных для получения ряда Тейлора. Устанавливая y = −4x и подставляя этот степенной ряд в выражение для c (x) и сдвигая индекс суммирования n на 1, разложение упрощается до

c (x) = ∑ n = 0 ∞ (2 nn) xnn + 1. {\ displaystyle c (x) = \ sum _ {n = 0} ^ {\ infty} {2n \ choose n} {\ frac {x ^ {n}} {n + 1}}.}

c(x)=\sum _{n=0}^{\infty }{2n \choose n}{\frac {x^{n}}{n+1}}.

Коэффициенты теперь искомая формула для C n.

Другой способ получить c (x) - решить относительно xc (x) и заметить, что $∫ 0 xtndt {\ displaystyle \ int _ {0} ^ {x} \! t ^ {n} \, dt}$ $\int _{0}^{x}\!t^{n}\,dt$ появляется в каждом члене степенного ряда.

Вторая проба

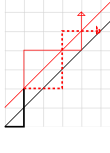Рис. 1. Неверный участок пути (сплошной красный цвет) перевернут. Плохие пути достигают (n - 1, n + 1) вместо (n, n).

Это доказательство зависит от трюка, известного как метод отражения Андре, который первоначально использовался в связи с Теорема Бертрана. (Принцип отражения широко приписывался Дезире Андре, но его метод фактически не использовал отражения; а метод отражения - разновидность Эбли и Мириманофф.) Мы считаем пути, которые начинаются и заканчиваются на диагональ сетки n × n. Все такие пути имеют n ступенек вправо и n ступенек вверх. Поскольку мы можем выбрать, какой из 2n шагов является восходящим (или, что то же самое, вправо), всего всего $(2 nn) {\ displaystyle {\ tbinom {2n} {n}}}$ ${\ tbinom {2n} {n}}$ монотонные пути этого типа. Плохой путь пересечет главную диагональ и коснется следующей более высокой (фатальной) диагонали (обозначенной красным на рисунке). Мы переворачиваем часть пути, возникшую после этого касания, по этой фатальной диагонали, как показано на рисунке; эта геометрическая операция сводится к тому, что после этого касания меняются местами все шаги вправо и вверх. На участке пути, который не отражается, на один шаг вверх больше, чем на шаги вправо, поэтому оставшийся участок неправильного пути имеет на один шаг вправо больше, чем шаг вверх (потому что он заканчивается на главной диагонали). Когда эта часть пути отражается, она также будет иметь на один шаг вверх больше, чем шаги вправо. Поскольку осталось еще 2n шагов, теперь должно быть n + 1 шагов вверх и n - 1 шагов вправо. Таким образом, вместо достижения цели (n, n) все плохие пути (после отражения части пути) будут заканчиваться в месте (n - 1, n + 1). Поскольку любой монотонный путь в сетке (n - 1) × (n + 1) должен встречаться с фатальной диагональю, этот процесс отражения устанавливает взаимно однозначное соответствие между плохими путями исходной сетки и монотонными путями этой новой сетки, поскольку отражение процесс обратим. Таким образом, количество неверных путей равно

(n - 1 + n + 1 n - 1) = (2 nn - 1) = (2 nn + 1) {\ displaystyle {n-1 + n + 1 \ choose n-1} = {2n \ choose n-1} = {2n \ choose n + 1}}

{n-1 + n + 1 \ choose n-1} = {2n \ choose n-1} = { 2n \ choose n + 1}

и количество каталонских путей (то есть хороших путей) получается удалением количества плохих путей из общего числа количество монотонных путей исходной сетки,

C n = (2 nn) - (2 nn + 1). {\ displaystyle C_ {n} = {2n \ choose n} - {2n \ choose n + 1}.}

C_{n}={2n \choose n}-{2n \choose n+1}.

В терминах слов Дика мы начинаем с (не-Дайковской) последовательности из n X и n Y и поменять местами все X и Y после первого Y, которое нарушает условие Дейка. В этом первом Y есть k + 1 Y и k X для некоторого k от 1 до n - 1.

Третье доказательство

Следующее биективное доказательство, хотя и более сложное, чем предыдущее. один, обеспечивает более естественное объяснение члену n + 1, фигурирующему в знаменателе формулы для C n. Обобщенную версию этого доказательства можно найти в статье Rukavicka Josef (2011).

Рисунок 2. Путь с превышением 5.

Предположим, нам дан монотонный путь, который может пересекать диагональ. Excedance пути определяется как количество вертикальных ребер, которые лежат выше диагонали. Например, на рисунке 2 ребра, лежащие выше диагонали, отмечены красным, поэтому превышение пути равно 5.

Теперь, если нам дан монотонный путь, превышение которого не равно нулю, тогда мы может применить следующий алгоритм для построения нового пути, превышение которого на единицу меньше того, с которого мы начали.

Начиная с нижнего левого угла, следуйте по траектории, пока она не пройдет выше диагонали.
Продолжайте следовать по траектории, пока она снова не коснется диагонали. Обозначьте X первое такое ребро, которое было достигнуто.
Поменяйте местами часть пути, идущую до X, на часть, идущую после X.

Следующий пример должен прояснить это. На рисунке 3 черная точка указывает точку, где путь сначала пересекает диагональ. Черный край - это X, и мы меняем местами красную часть с зеленой частью, чтобы создать новый путь, показанный на второй диаграмме.

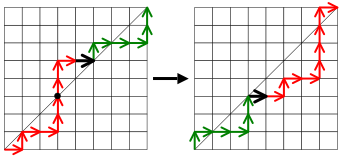Рисунок 3. Зеленая и красная части меняются местами.

Превышение снизилось с трех до двух. Фактически, алгоритм приведет к уменьшению превышения на единицу для любого пути, по которому мы его подаем, потому что первый вертикальный шаг, начинающийся по диагонали (в точке, отмеченной черной точкой), является уникальным вертикальным краем, который под действием операции проходит сверху по диагонали вниз; все остальные вертикальные края остаются на той же стороне диагонали.

Рис. 4. Все монотонные пути в сетке 3 × 3, иллюстрирующие алгоритм уменьшения превышения.

Также нетрудно увидеть, что этот процесс обратим: для любого пути P, превышение которого меньше n, существует ровно один путь, который дает P при применении к нему алгоритма. Действительно, (черный) край X, который изначально был первым горизонтальным шагом, заканчивающимся на диагонали, стал последним горизонтальным шагом, начинающимся на диагонали.

Это означает, что количество путей превышения n равно количеству путей превышения n - 1, что равно количеству путей превышения n - 2, и так далее, вплоть до нуля.. Другими словами, мы разделили набор всех монотонных путей на n + 1 классов одинакового размера, соответствующих возможным превышениям между 0 и n. Поскольку существуют

(2 n n) {\ displaystyle {2n \ choose n}}

{2n \ choose n}

монотонные пути, мы получаем искомую формулу

C n = 1 n + 1 (2 n n). {\ displaystyle C_ {n} = {\ frac {1} {n + 1}} {2n \ choose n}.}

C_ {n} = {\ frac {1} {n + 1}} {2n \ choose n}.

На рисунке 4 показана ситуация для n = 3. Каждый из 20 возможных монотонных путей где-то появляется. в таблице. В первом столбце показаны все пути превышения трех, которые полностью лежат выше диагонали. Столбцы справа показывают результат последовательных применений алгоритма, при этом превышение уменьшается на единицу за раз. Всего пять строк, то есть C 3 = 5.

Четвертое доказательство

В этом доказательстве используется определение триангуляции каталонских чисел для установления связи между C n и C n + 1. Для многоугольника P с n + 2 сторонами сначала отметьте одну из его сторон как основание. Если затем P триангулирован, мы можем дополнительно выбрать и сориентировать одно из его 2n + 1 ребер. Всего таких декорированных триангуляций (4n + 2) C n. Теперь, когда у многоугольника Q n + 3 стороны, снова отметьте одну из его сторон как основание. Если Q триангулирован, мы можем дополнительно отметить одну из сторон, отличную от основной. Всего таких декорированных триангуляций (n + 2) C n + 1. Тогда существует простое взаимно однозначное соответствие между этими двумя типами декорированных триангуляций: мы можем либо свернуть треугольник в Q, сторона которого отмечена, либо наоборот, развернуть ориентированное ребро в P до треугольника и отметить его новую сторону. Таким образом,

(4 n + 2) C n = (n + 2) C n + 1. {\ displaystyle (4n + 2) C_ {n} = (n + 2) C_ {n + 1}.}

(4n + 2) C_ {n} = (n + 2) C_ {n + 1}.

Биномиальная формула для C n сразу следует из этого соотношения и начального условия C 1 = 1.

Пятое доказательство

Это доказательство основано на интерпретации слов Дика каталонских чисел, поэтому C n - количество способов правильно сопоставить n пар скобок. Мы обозначаем (возможно, пустую) правильную строку с помощью c, а ее обратную строку (где "[" и "]" меняются местами) с помощью c. Поскольку любой c может быть однозначно разложен на c = [c 1 ] c 2, суммирование по возможным точкам для размещения закрывающей скобки немедленно дает рекурсивное определение

C 0 = 1 и С n + 1 знак равно ∑ я знак равно 0 N С я С N - я для n ≥ 0. {\ displaystyle C_ {0} = 1 \ quad {\ text {and}} \ quad C_ {n + 1} = \ sum _ {i = 0} ^ {n} C_ {i} \, C_ {ni} \ quad {\ text {for}} n \ geq 0.}

C_ {0} = 1 \ quad {\ text {and}} \ quad C_ {n + 1} = \ sum _ {i = 0 } ^ {n} C_ {i} \, C_ {ni} \ quad {\ text {for}} n \ geq 0.

Теперь пусть b обозначает сбалансированную строку длины 2n, то есть содержит равное количество «[» и «]» - и $B n = (2 nn) = dn C n {\ displaystyle \ textstyle B_ {n} = {2n \ choose n} = d_ {n} C_ {n}}$ $\ textstyle B_ {n} = {2n \ choose n} = d_ {n} C_ {n}$ с некоторым множителем d n ≥ 1. Как и выше, любая сбалансированная строка может быть однозначно разложена на [c] b или] c [b, поэтому

B n + 1 = 2 ∑ i = 0 n B i C n - i. {\ displaystyle B_ {n + 1} = 2 \ sum _ {i = 0} ^ {n} B_ {i} C_ {ni}.}

B_{n+1}=2\sum _ {i=0}^{n}B_{i}C_{n-i}.

Кроме того, любая неверно сбалансированная строка начинается с c], поэтому

Б N + 1 - С N + 1 знак равно ∑ я знак равно 0 N (2 я + 1 я) С N - я знак равно ∑ я знак равно 0 N 2 я + 1 я + 1 Б я С N - я. {\ displaystyle B_ {n + 1} -C_ {n + 1} = \ sum _ {i = 0} ^ {n} {2i + 1 \ select i} C_ {ni} = \ sum _ {i = 0} ^ {n} {\ frac {2i + 1} {i + 1}} B_ {i} C_ {ni}.}

B_{n+1}-C_{n+1}=\sum _{i=0}^{n}{ 2i+1 \choose i}C_{ni}=\sum _{i=0}^{n}{\frac {2i+1}{i+1}}B_{i}C_{ni}.

Вычитая приведенные выше уравнения и используя B i = d iCiдает

C n + 1 = 2 ∑ i = 0 ndi C i C n - i - ∑ i = 0 n 2 i + 1 i + 1 di C i C n - i = ∑ i = 0 ndii + 1 C i C n - i. {\ displaystyle C_ {n + 1} = 2 \ sum _ {i = 0} ^ {n} d_ {i} C_ {i} C_ {ni} - \ sum _ {i = 0} ^ {n} {\ гидроразрыв {2i + 1} {i + 1}} d_ {i} C_ {i} C_ {ni} = \ sum _ {i = 0} ^ {n} {\ frac {d_ {i}} {i + 1 }} C_ {i} C_ {ni}.}

C_{n+1}=2\sum _{i=0}^{n}d_{i}C_{i}C_{n-i}-\sum _{i=0}^{n}{\frac {2i+1}{i+1}}d_{i}C_{i}C_{n-i}=\sum _{i=0}^{n}{\frac {d_{i}}{i+1}}C_{i}C_{n-i}.

Сравнение коэффициентов с исходной формулой рекурсии для C n дает d i = i + 1, поэтому

C п = 1 п + 1 (2 нн). {\ displaystyle C_ {n} = {\ frac {1} {n + 1}} {2n \ choose n}.}

C_ {n} = {\ frac {1} {n + 1}} {2n \ choose n}.

Шестое доказательство

Это простое доказательство также основано на Слова Дика интерпретируют каталонские числа, но используют красивую лемму Цикла Дворецкого и Моцкина. Назовите последовательность X и Y доминирующими, если при чтении слева направо дисбаланс всегда положительный, то есть количество X всегда строго больше, чем количество Y. Лемма цикла утверждает, что любая последовательность $m {\ displaystyle m}$ $m$ X и $n {\ displaystyle n}$ $n$ Y, где $m>n { \ displaystyle m>n}$ $m>n$ , имеет точно $m - n {\ displaystyle mn}$ $m-n$ доминирующих циклических перестановок. Чтобы увидеть это, просто расположите заданную последовательность из $m + n {\ displaystyle m + n}$ $m+n$ X и Y по кругу и несколько раз удаляйте соседние пары XY, пока не останется только $m - n {\ displaystyle mn}$ $m-n$ X. Каждый из этих X был началом доминирующая циклическая перестановка до того, как что-либо было удалено. В частности, когда $m = n + 1 {\ displaystyle m = n + 1}$ ${\ displaystyle m = n + 1}$ , существует ровно одна доминирующая циклическая перестановка. Удаление ведущего X из он (доминирующая последовательность должна начинаться с X) оставляет последовательность Дика. Поскольку существует $C n = 1 2 n + 1 (2 n + 1 n) = 1 n + 1 (2 nn) {\ displaystyle C_ {n} = {\ frac {1} {2n + 1}} {2n + 1 \ choose n} = {\ frac {1} {n + 1}} {2n \ choose n}}$ ${\ displaystyle C_ {n} = {\ frac {1} {2n + 1}} {2n + 1 \ choose n} = {\ frac {1} {n + 1}} {2n \ choose n}}$ различных циклов $n + 1 {\ displaystyle n + 1}$ $n + 1$ X и $n {\ displaystyle n}$ $n$ Y, каждая из которых соответствует ровно одной последовательности Дика, $C n {\ displaystyle C_ {n}}$ $C_{n}$ подсчитывает последовательности Дика.

Матрица Ганкеля

Матрица Ганкеля n × n , чья запись (i, j) является каталонским числом C i + j − 2, имеет определитель 1, независимо от значения n. Например, для n = 4 имеем

det [1 1 2 5 1 2 5 14 2 5 14 42 5 14 42 132] = 1. {\ displaystyle \ det {\ begin {bmatrix} 1 1 2 5 \\ 1 2 5 14 \ \ 2 5 14 42 \\ 5 14 42 132 \ end {bmatrix}} = 1.}

\det {\begin{bmatrix}1125\\12514\\251442\\51442132\end{bmatrix}}=1.

Более того, если индексация "сдвинута" так, что запись (i, j) заполнена каталонским числом C i + j− 1, то определитель по-прежнему равен 1, независимо от значения n. Например, для n = 4 имеем

det [1 2 5 14 2 5 14 42 5 14 42 132 14 42 132 429] = 1. {\ displaystyle \ det {\ begin {bmatrix} 1 2 5 14 \\ 2 5 14 42 \ \ 5 14 42 132 \\ 14 42 132 429 \ end {bmatrix}} = 1.}

\det {\begin{bmatrix}12514\\251442\\51442132\\1442132429\end{bmatrix}}=1.

Взятые вместе, эти два условия однозначно определяют каталонские числа.

История

Каталонские числа в книге Минганту «Быстрый метод получения точного соотношения деления круга, том III»

Каталонская последовательность была описана в 18 веке Леонардом Эйлером, которого интересовало количество различных способов деления многоугольника на треугольники. Последовательность названа в честь Эжена Шарля Каталана, который обнаружил связь с выражениями, заключенными в скобки, во время исследования загадки Ханойских башен. Уловка подсчета слов Дейка была обнаружена Дезире Андре в 1887 году.

В 1988 году выяснилось, что каталонская числовая последовательность использовалась в Китае монгольским математиком Минганту к 1730 году. Именно тогда он начал писать свою книгу «Гэ Юань Ми Лу Цзе Фа» [Быстрый метод получения точного отношения деления круга], которую завершил его ученик Чэнь Цзисинь в 1774 году, но опубликован шестьдесят лет спустя. Питер Дж. Ларкомб (1999) обрисовал некоторые особенности творчества Минганту, в том числе стимул Пьера Жарту, который принес три бесконечных серии в Китай в начале 1700-х годов.

Например, Мин использовал каталонскую последовательность, чтобы выразить разложение последовательностей sin (2α) и sin (4α) через sin (α).

Обобщения

Двухпараметрическая последовательность неотрицательных целых чисел $(2 м)! (2 п)! (м + п)! м! п! {\ displaystyle {\ frac {(2m)! (2n)!} {(m + n)! m! n!}}}$ ${\ frac {(2m)! (2n)!} {(M + n)! M! N !}}$ - это обобщение каталонских чисел. Они были названы суперкаталонскими числами от Айры Гессель. Эти числа не следует путать с числами Шредера-Гиппарха, которые иногда также называют суперкаталонскими числами.

Для $m = 1 {\ displaystyle m = 1}$ $m=1$ это всего лишь в два раза больше обычных каталонских чисел, а для $m = n {\ displaystyle m = n}$ $m = n$ числа имеют простое комбинаторное описание. Однако другие комбинаторные описания известны только для $m = 2, 3 {\ displaystyle m = 2,3}$ ${\ displaystyle m = 2,3}$ и $4 {\ displaystyle 4}$ $4$ , и найти общую комбинаторную интерпретацию - открытая проблема.

Сергей Фомин и Натан Ридинг дали обобщенное каталонское число, ассоциированное с любой конечной кристаллографической группой Кокстера, а именно количество полностью коммутативных элементов группы; в терминах ассоциированной корневой системы , это количество антицепей (или идеалов порядка) в наборе положительных корней. Классическое каталонское число $C n {\ displaystyle C_ {n}}$ $C_{n}$ соответствует корневой системе типа $A n {\ displaystyle A_ {n}}$ $A_ {n}$ . Классическое рекуррентное соотношение обобщает: каталонское число диаграммы Кокстера равно сумме каталонских чисел всех ее максимальных собственных поддиаграмм.

См. Также

Математический портал

Примечания

Ссылки

Стэнли, Ричард П. (2015), каталонские числа. Cambridge University Press, ISBN 978-1-107-42774-7.
Конвей и Гай (1996) Книга чисел. Нью-Йорк: Коперник, стр. 96–106.
Гарднер, Мартин (1988), Путешествие во времени и другие математические недоумения, Нью-Йорк: W.H. Freeman and Company, pp. 253–266 (Ch. 20), ISBN 0-7167-1924-X
Коши, Томас (2008), Каталонские числа с приложениями, Oxford University Press, ISBN 978-0-19-533454-8
Koshy, Thomas Zhenguang Gao (2011) «Некоторые свойства делимости каталонского языка. числа », Mathematical Gazette 95: 96–102.
Ларкомб, П.Дж. (1999). «Китайское открытие 18 века каталонских чисел» (PDF). Математический спектр. 32: 5–7.
Стэнли, Ричард П. (1999), Перечислительная комбинаторика. Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, ISBN 978-0-521-56069-6, MR 1676282
Egecioglu, Omer (2009), Каталонская оценка детерминанта Ханкеля (PDF)
Георгичук, Ирина; Orelowitz, Gidon (2020), Супер-каталонские числа третьего и четвертого рода, arXiv : 2008.00133

Внешние ссылки

Стэнли, Ричард П. ( 1998), Каталонское приложение к Перечислительной комбинаторике, том 2 (PDF)
Вайсштейн, Эрик У. «Каталонское число». MathWorld.
Дикау, Роберт М.: Каталонские числа Дополнительные примеры.
Дэвис, Том: Каталонские числа. Еще примеры.
«Эквивалентность трех каталонских интерпретаций чисел» из проекта Wolfram Demonstrations Project [1]
Учебные материалы, относящиеся к числовым треугольникам, связанным с разделами в Викиверситете