Logit

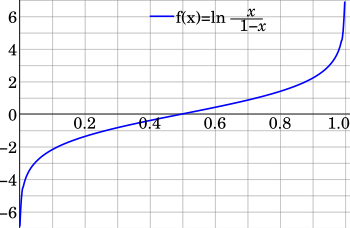
График логита (p) в диапазоне от 0 до 1, где основание логарифма равно e.

В статистике logit () или log-odds - это логарифм числа шансы $p\; 1\; -\; p\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{p\}\; \{1-p\}\}\}$где p - вероятность. Это тип функции, которая создает карту значений вероятности от $(0,\; 1)\; \{\backslash \; displaystyle\; (0,1)\}$до $(-\; \infty ,\; +\; \infty )\; \{\backslash \; displaystyle\; (-\; \backslash \; infty,\; +\; \backslash \; infty)\}$. Это инверсия сигмоидальной «логистической» функции или логистического преобразования, используемых в математике, особенно в статистике.

• 1 Определение
• 2 История
• 3 Использование и свойства
• 4 Сравнение с пробитом
• 5 См. Также
• 6 Ссылки
• 7 Дополнительная литература

Если p представляет собой вероятность, то p / (1 - p) представляет собой соответствующие шансы ; логит вероятности - это логарифм шансов, т.е.

$logit\; \; (p)\; =\; log\; \; (p\; 1\; -\; p)\; =\; log\; \; (p)\; -\; log\; \; (1\; -\; p)\; =\; -\; log\; \; (1\; п\; -\; 1).\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{logit\}\; (p)\; =\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{p\}\; \{1-p\}\}\; \backslash \; right)\; =\; \backslash \; log\; (p)\; -\; \backslash \; log\; (1-p)\; =\; -\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{p\}\}\; -\; 1\; \backslash \; right)\; \backslash ,.\}$

Основание используемой функции логарифма не имеет большого значения в данной статье, если оно больше 1, но чаще всего используется натуральный логарифм с основанием e. Выбор основания соответствует выбору логарифмической единицы для значения: основание 2 соответствует шеннону, основание e соответствует «nat », а основание 10 на Хартли ; эти единицы особенно используются в теоретико-информационных интерпретациях. Для каждого выбора базы функция логита принимает значения от отрицательной до положительной бесконечности.

«логистическая» функция любого числа $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$задается обратным логитом:

$logit\; -\; 1\; \; (\alpha )\; знак\; равно\; логистический\; \; (\alpha )\; =\; 1\; 1\; +\; ехр\; \; (-\; \alpha )\; =\; ехр\; \; (\alpha )\; ехр\; \; (\alpha )\; +\; 1\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{logit\}\; ^\; \{-\; 1\}\; (\backslash \; альфа)\; =\; \backslash \; operatorname\; \{logistic\}\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{1\}\; \{1+\; \backslash \; operatorname\; \{exp\}\; (-\; \backslash \; alpha)\}\}\; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{exp\}\; (\backslash \; alpha)\}\; \{\backslash \; operatorname\; \{exp\}\; (\backslash \; alpha)\; +1\}\}\}$

Разница между логитами двух вероятностей - это логарифм отношения шансов (R), что обеспечивает сокращение для записи правильной комбинации отношения шансов только добавлением и вычитанием :

$log\; \; (R)\; =\; log\; \; (p\; 1\; /\; (1\; -\; p\; 1)\; p\; 2\; /\; (1\; -\; p\; 2))\; =\; log\; \; (p\; 1\; 1\; -\; p\; 1)\; -\; журнал\; \; (p\; 2\; 1\; -\; p\; 2)\; =\; logit\; \; (p\; 1)\; -\; logit\; \; (p\; 2).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{log\}\; (R)\; =\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{\{p\_\; \{1\}\}\; /\; (1-p\_\; \{1\})\}\; \{\{p\_\; \{2\}\}\; /\; (1-p\_\; \{\; 2\})\}\}\; \backslash \; right)\; =\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{p\_\; \{1\}\}\; \{1-p\_\; \{1\}\}\}\; \backslash \; right)\; -\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{p\_\; \{2\}\}\; \{1-p\_\; \{2\}\}\}\; \backslash \; right)\; =\; \backslash \; operatorname\; \{logit\}\; (p\_\; \{1\})\; -\; \backslash \; operatorname\; \{logit\}\; (p\_\; \{2\})\; \backslash ,.\}$

Было предпринято несколько попыток адаптировать методы линейной регрессии к области, в которой выходными данными является значение вероятности $(0,\; 1)\; \{\backslash \; displaystyle\; (0,1)\}$вместо любого действительного числа. $(-\; \infty ,\; +\; \infty )\; \{\backslash \; displaystyle\; (-\; \backslash \; infty,\; +\; \backslash \; infty)\}$. Во многих случаях такие усилия были сосредоточены на моделировании этой проблемы путем сопоставления диапазона $(0,\; 1)\; \{\backslash \; displaystyle\; (0,1)\}$с $(-\; \infty ,\; +\; \infty )\; \{\backslash \; displaystyle\; (-\; \backslash \; infty,\; +\; \backslash \; infty)\}$, а затем запускает линейную регрессию для этих преобразованных значений. В 1934 году Честер Иттнер Блисс использовал кумулятивную функцию нормального распределения для выполнения этого сопоставления и назвал свою модель пробит сокращением для «вероятность способности и это ";. Однако это более затратно в вычислительном отношении. В 1944 году Джозеф Берксон использовал логарифм шансов и назвал эту функцию logit, сокращение от «log istic un it », следуя аналогии с пробит. Логарифмические коэффициенты широко использовались Чарльзом Сандерсом Пирсом (конец XIX века). Г. А. Барнард в 1949 г. ввел широко используемый термин логарифм-шансы; log-шансы события - это логит вероятности события.

• logit в логистической регрессии - особый случай функции связи в обобщенной линейной модели : это каноническая функция связи для распределения Бернулли.
• Функция logit является отрицательной от производной от бинарной энтропийной функции.
• logit также является центральным в вероятностной модели Раша для измерения, который, среди прочего, применяется в психологической и образовательной оценке.
• Функция обратного логита (то есть логистическая функция ) также иногда называется функция экспита.
• В эпидемиологии болезней растений логит используется для подгонки данных к логистической модели. В моделях Гомперца и мономолекулярной модели все три известны как модели семейства Ричардсов.
• Логарифмическая функция вероятностей часто используется в алгоритмах оценки состояния из-за ее численных преимуществ в случае малые вероятности. Вместо умножения очень маленьких чисел с плавающей запятой, вероятности логарифмических шансов можно просто суммировать для вычисления совместной вероятности (логарифм-шансов).

Сравнение логит-функции с масштабированный пробит (т.е. обратный CDF нормального распределения ), сравнивающий $логит\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{logit\}\; (x)\}$vs. $\Phi \; -\; 1\; (x)\; \pi \; /\; 8\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{\backslash \; Phi\; ^\; \{-\; 1\}\; (x)\}\; \{\backslash ,\; \{\backslash \; sqrt\; \{\backslash \; pi\; /\; 8\; \backslash ,\}\}\; \backslash ,\}\}\}$, что делает наклоны одинаковыми в исходной точке y.

Тесно связаны с функцией логита (и моделью логита ): функция пробита и пробит модель. Логит и пробит являются сигмоидными функциями с областью между 0 и 1, что делает их обе квантильными функциями, т. Е. Обратными кумулятивной функции распределения ( CDF) распределения вероятностей. Фактически, логит - это функция квантиля логистического распределения, а пробит - функция квантиля нормального распределения. Функция пробит обозначается $\Phi \; -\; 1\; (x)\; \{\backslash \; displaystyle\; \backslash \; Phi\; ^\; \{-\; 1\}\; (x)\}$, где $\Phi \; (x)\; \{\backslash \; displaystyle\; \backslash \; Phi\; (x)\}$- это CDF нормального распределения, как только что упоминалось:

$\Phi \; (x)\; =\; 1\; 2\; \pi \; \int \; -\; \infty \; xe\; -\; y\; 2\; 2\; dy.\; \{\backslash \; displaystyle\; \backslash \; Phi\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{x\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{y\; ^\; \{2\}\; \}\; \{2\}\}\}\; dy.\}$

Как показано на графике справа, функции logit и probit очень похожи, когда функция probit масштабируется, так что ее наклон при y = 0 совпадает с наклоном logit. В результате пробит-модели иногда используются вместо логит-моделей, потому что для определенных приложений (например, в байесовской статистике ) реализация проще.

• сигмоидальная функция, обратная логит-функции
• Дискретный выбор для двоичного логита, полиномиальный логит, условный логит, вложенный логит, смешанный логит, разнесенный логит и упорядоченный логит
• Ограниченная зависимая переменная
• Дэниел Макфадден, лауреат Нобелевской премии по экономике за разработку конкретной логит-модели, используемой в экономике
• Логит-анализ в маркетинге
• Мультиномиальный logit
• Ogee, кривая подобной формы
• Perceptron
• Probit, другая функция с тем же доменом и диапазоном, что и logit
• Ridit scoring
• Преобразование данных (статистика)
• Arcsin (преобразование)

• Ashton, Winifred D. (1972). Преобразование логита: с особым упором на его использование в биотесте. Статистические монографии и курсы Гриффина. 32 . Чарльз Гриффин. ISBN 978-0-85264-212-2.