Сумма Римана

Четыре из суммирования Римана методов для аппроксимации площади под кривыми. Правый и левый методы делают аппроксимацию, используя правую и левую конечные точки каждого подынтервала соответственно. Методы максимума и минимума делают приближение с использованием наибольшего и наименьшего значений конечных точек каждого подынтервала соответственно. Значения сумм сходятся по мере того, как подынтервалы уменьшаются вдвое от верхнего левого угла к нижнему правому.

В математике, сумма Римана определенный вид аппроксимации интеграла конечной суммой. Он назван в честь немецкого математика XIX века Бернхарда Римана. Одним из наиболее распространенных приложений является аппроксимация площади функций или линий на графике, а также длины кривых и других приближений.

Сумма вычисляется путем разделения области на формы ( прямоугольники, трапеции, параболы или кубики ), которые вместе образуют область, аналогичную измеряемой области, затем вычисляются площади для каждой из этих форм и, наконец, складываются все эти формы. небольшие участки вместе. Этот подход можно использовать для поиска численного приближения для определенного интеграла, даже если основная теорема исчисления не позволяет легко найти решение в замкнутой форме.

Поскольку область, заполненная маленькими формами, обычно не имеет точно такую ​​же форму, как измеряемая область, сумма Римана будет отличаться от измеряемой площади. Эту ошибку можно уменьшить, разделив область более мелко, используя все меньшие и меньшие формы. По мере того, как формы становятся все меньше и меньше, сумма приближается к интегралу Римана.

• 1 Определение
• 2 Некоторые особые типы сумм Римана
• 3 метода
  • 3.1 Левая сумма Римана
  • 3.2 Правая сумма Римана
  • 3.3 Правило средней точки
  • 3.4 Трапециевидное правило
• 4 Подключение с интеграцией
• 5 Пример
• 6 Высшие измерения
  • 6.1 Два измерения
  • 6.2 Три измерения
  • 6.3 Произвольное количество измерений
  • 6.4 Обобщение
• 7 См. Также
• 8 ссылки
• 9 Внешние ссылки

Позвольте быть функцией, определенной на отрезке действительных чисел,, и ${\ displaystyle f: [a, b] \ rightarrow \ mathbb {R}}$ ${\ Displaystyle [а, б]}$${\ Displaystyle \ mathbb {R}}$

${\ displaystyle P = \ left \ {[x_ {0}, x_ {1}], [x_ {1}, x_ {2}], \ dots, [x_ {n-1}, x_ {n}] \ верно\}}$,

быть разбиением I, где

${\ displaystyle a = x_ {0} lt;x_ {1} lt;x_ {2} lt;\ cdots lt;x_ {n} = b}$.

Сумма Римана из F над I с перегородкой P определяется как ${\ displaystyle S}$

${\ displaystyle S = \ sum _ {i = 1} ^ {n} f (x_ {i} ^ {*}) \, \ Delta x_ {i}}$

где и. В зависимости от того, какие из них выбраны, можно получить разные суммы Римана. В конце концов, это не имеет значения, если функция интегрируема по Риману, когда разность или ширина слагаемых приближается к нулю. ${\ displaystyle \ Delta x_ {i} = x_ {i} -x_ {i-1}}$${\ displaystyle x_ {i} ^ {*} \ in [x_ {i-1}, x_ {i}]}$${\ displaystyle x_ {i} ^ {*}}$ ${\ displaystyle \ Delta x_ {i}}$

Конкретный выбор дает нам различные типы сумм Римана: ${\ displaystyle x_ {i} ^ {*}}$

• Если для всех i, то S называется левым правилом или левой суммой Римана.${\ Displaystyle х_ {я} ^ {*} = х_ {я-1}}$
• Если для всех i, то S называется правым правилом или правой суммой Римана.${\ Displaystyle х_ {я} ^ {*} = х_ {я}}$
• Если для всех i, то S называется правилом средней точки или средней суммой Римана.${\ Displaystyle х_ {я} ^ {*} = (х_ {я} + х_ {я-1}) / 2}$
• Если (то есть, верхняя грань из F над), то S определена, чтобы быть верхней суммой Римана или верхняя сумма Дарбу.${\ displaystyle f (x_ {i} ^ {*}) = \ sup f ([x_ {i-1}, x_ {i}])}$ ${\ Displaystyle [х_ {я-1}, х_ {я}]}$
• Если (то есть, нижняя грань из F над), то S определено быть меньшую сумму Римана или понизить Дарбу сумму.${\ displaystyle f (x_ {i} ^ {*}) = \ inf f ([x_ {i-1}, x_ {i}])}$ ${\ Displaystyle [х_ {я-1}, х_ {я}]}$

Все эти методы являются одними из самых основных способов выполнения численного интегрирования. Грубо говоря, функция является интегрируемой по Риману, если все суммы Римана сходятся по мере того, как разбиение «становится все более и более тонким».

Хотя среднее значение левой и правой сумм Римана не выводится как сумма Римана, это трапециевидная сумма и один из самых простых способов аппроксимации интегралов с использованием средневзвешенных значений. За этим по сложности следуют правило Симпсона и формулы Ньютона – Котеса.

Любая сумма Римана на данном разбиении (то есть при любом выборе между и) содержится между нижней и верхней суммами Дарбу. Это составляет основу интеграла Дарбу, который в конечном итоге эквивалентен интегралу Римана. ${\ displaystyle x_ {i} ^ {*}}$${\ displaystyle x_ {i-1}}$${\ displaystyle x_ {i}}$

Четыре метода суммирования Римана обычно лучше всего подходят для разбиений равного размера. Таким образом, интервал [ a, b ] делится на подинтервалы, каждый из которых имеет длину ${\ displaystyle n}$

${\ displaystyle \ Delta x = {\ frac {ba} {n}}.}$

Тогда точки в разделе будут

${\ Displaystyle a, \; a + \ Delta x, \; a + 2 \ Delta x, \; \ ldots, \; a + (n-2) \ Delta x, \; a + (n-1) \ Delta x, \; b.}$

Левая сумма Римана

Левая сумма Римана x ³ на [0,2] с использованием 4 делений

Для левой суммы Римана аппроксимация функции ее значением в левой конечной точке дает несколько прямоугольников с основанием Δ x и высотой f ( a + i Δ x). Выполнение этого для i = 0, 1,…, n  - 1 и сложение результирующих областей дает

${\ Displaystyle A _ {\ mathrm {left}} = \ Delta x \ left [f (a) + f (a + \ Delta x) + f (a + 2 * \ Delta x) + \ cdots + f (b- \ Дельта x) \ вправо].}$

Влево сумма Римана составляет завышению, если F является монотонно убывает на этом интервале, и недооценке, если она монотонно возрастает.

Правая сумма Римана

Правая сумма Римана x ³ на [0,2] с использованием 4 делений

Здесь f аппроксимируется значением в правой конечной точке. Это дает несколько прямоугольников с основанием Δ x и высотой f ( a + i  Δ x). Выполнение этого для i = 1,…, n и сложение результирующих областей дает

${\ Displaystyle A _ {\ mathrm {right}} = \ Delta x \ left [f (a + \ Delta x) + f (a + 2 \, \ Delta x) + \ cdots + f (b) \ right].}$

Правая сумма Римана составляет недооценке, если F является монотонно убывающей, и завышению, если она монотонно возрастает. Ошибка этой формулы будет

${\ displaystyle \ left \ vert \ int _ {a} ^ {b} f (x) \, dx-A _ {\ mathrm {right}} \ right \ vert \ leq {\ frac {M_ {1} (ba) ^ {2}} {2n}}}$,

где максимальное значение абсолютной величины в на интервале. ${\ displaystyle M_ {1}}$ ${\ Displaystyle е ^ {\ прайм} (х)}$

Правило средней точки

Средняя сумма Римана x ³ на [0,2] с использованием 4 делений.

Аппроксимация f в середине интервалов дает f ( a + Δ x / 2) для первого интервала, для следующего f ( a + 3Δ x / 2) и так далее, пока f ( b  - Δ x / 2). Подводя итог по областям, мы получаем

${\ displaystyle A _ {\ mathrm {mid}} = \ Delta x \ left [f (a + {\ tfrac {\ Delta x} {2}}) + f (a + {\ tfrac {3 \, \ Delta x} { 2}}) + \ cdots + f (b - {\ tfrac {\ Delta x} {2}}) \ right]}$.

Ошибка этой формулы будет

${\ displaystyle \ left \ vert \ int _ {a} ^ {b} f (x) \, dx-A _ {\ mathrm {mid}} \ right \ vert \ leq {\ frac {M_ {2} (ba) ^ {3}} {24n ^ {2}}}}$,

где максимальное значение абсолютной величины в на интервале. ${\ displaystyle M_ {2}}$ ${\ Displaystyle е ^ {\ прайм \ прайм} (х)}$

Трапециевидная линейка

Трапециевидная сумма Римана x ³ на [0,2] с использованием 4 делений. Основная статья: Трапециевидное правило

В этом случае значения функции f на интервале аппроксимируются средним значением значений на левой и правой конечных точках. Таким же образом, как и выше, простой расчет с использованием формулы площади

${\ displaystyle A = {\ tfrac {1} {2}} h (b_ {1} + b_ {2})}$

для трапеции с параллельными сторонами b 1, b 2 и высотой h производит

${\ Displaystyle A _ {\ mathrm {trap}} = {\ tfrac {1} {2}} \, \ Delta x \ left [f (a) + 2f (a + \ Delta x) + 2f (a + 2 \, \ Delta x) + \ cdots + f (b) \ right].}$

Ошибка этой формулы будет

${\ displaystyle \ left \ vert \ int _ {a} ^ {b} f (x) \, dx-A _ {\ mathrm {trap}} \ right \ vert \ leq {\ frac {M_ {2} (ba) ^ {3}} {12n ^ {2}}},}$

где - максимальное значение модуля. ${\ displaystyle M_ {2}}$${\ Displaystyle е ^ {\ прайм \ прайм} (х)}$

Приближение, полученное с помощью правила трапеций для функции, такое же, как среднее значение левой и правой сумм этой функции.

Для одномерной суммы Римана по области, когда максимальный размер элемента разбиения сжимается до нуля (то есть предел нормы разбиения стремится к нулю), для некоторых функций все суммы Римана сходятся к одному и тому же значению. Это предельное значение, если оно существует, определяется как определенный интеграл Римана функции по области, ${\ Displaystyle [а, б]}$

${\ displaystyle \ int _ {a} ^ {b} \! е (x) \, dx = \ lim _ {\ | \ Delta x \ | \ rightarrow 0} \ sum _ {i = 1} ^ {n} f (x_ {i} ^ {*}) \, \ Delta x_ {i}.}$

Для домена конечного размера, если максимальный размер элемента раздела уменьшается до нуля, это означает, что количество элементов раздела стремится к бесконечности. Для конечных разбиений суммы Римана всегда являются приближениями к предельному значению, и это приближение становится лучше по мере того, как разбиение становится более точным. Следующие анимации помогают продемонстрировать, как увеличение количества разделов (при уменьшении максимального размера элемента раздела) лучше соответствует «площади» под кривой:

• 

  Левая сумма

• 

  Правильная сумма

• 

  Средняя сумма

Поскольку здесь предполагается, что красная функция является гладкой функцией, все три суммы Римана сходятся к одному и тому же значению, когда количество разбиений стремится к бесконечности.

Сравнение правых сумм функции y = x ² от 0 до 2 с интегралом от нее от 0 до 2. Визуальное представление площади под кривой y = x ² для интервала от 0 до 2. С использованием первообразных эта площадь составляет ровно 8/3. Аппроксимация площади от 0 до 2 с использованием сумм по правому правилу. 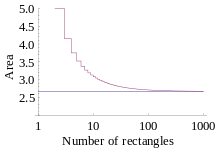Обратите внимание, что поскольку функция монотонно возрастает, правая сумма всегда будет завышать площадь, вносимую каждым членом в сумму (и делать это максимально).${\ Displaystyle у = х ^ {2}}$ Значение суммы Римана под кривой y = x ² от 0 до 2. По мере увеличения количества прямоугольников оно приближается к точной площади 8/3.

Например, площадь под кривой y = x ² между 0 и 2 может быть вычислена процедурно с использованием метода Римана.

Интервал [0, 2] сначала делится на n подинтервалов, каждому из которых дается ширина ; это ширина прямоугольников Римана (далее «коробки»). Поскольку должна использоваться правая сумма Римана, последовательность координат x для ящиков будет. Следовательно, последовательность высот ящиков будет. Это важный факт, и. ${\ Displaystyle {\ tfrac {2} {п}}}$${\ Displaystyle x_ {1}, x_ {2}, \ ldots, x_ {n}}$${\ Displaystyle x_ {1} ^ {2}, x_ {2} ^ {2}, \ ldots, x_ {n} ^ {2}}$${\ displaystyle x_ {i} = {\ tfrac {2i} {n}}}$${\ displaystyle x_ {n} = 2}$

Площадь каждого квадрата будет равна, и, следовательно, n- я правая сумма Римана будет: ${\ displaystyle {\ tfrac {2} {n}} \ times x_ {i} ^ {2}}$

${\ displaystyle {\ begin {align} S amp; = {\ frac {2} {n}} \ times \ left ({\ frac {2} {n}} \ right) ^ {2} + \ cdots + {\ frac {2} {n}} \ times \ left ({\ frac {2i} {n}} \ right) ^ {2} + \ cdots + {\ frac {2} {n}} \ times \ left ({\ frac {2n} {n}} \ right) ^ {2} \\ amp; = {\ frac {8} {n ^ {3}}} \ left (1+ \ cdots + i ^ {2} + \ cdots + n ^ {2} \ right) \\ amp; = {\ frac {8} {n ^ {3}}} \ left ({\ frac {n (n + 1) (2n + 1)} {6}} \ справа) \\ amp; = {\ frac {8} {n ^ {3}}} \ left ({\ frac {2n ^ {3} + 3n ^ {2} + n} {6}} \ right) \\ amp; = {\ frac {8} {3}} + {\ frac {4} {n}} + {\ frac {4} {3n ^ {2}}} \ end {align}}}$

Если рассматривать предел как n → ∞, можно сделать вывод, что приближение приближается к фактическому значению площади под кривой по мере увеличения количества прямоугольников. Следовательно:

${\ displaystyle \ lim _ {n \ to \ infty} S = \ lim _ {n \ to \ infty} \ left ({\ frac {8} {3}} + {\ frac {4} {n}} + {\ frac {4} {3n ^ {2}}} \ right) = {\ frac {8} {3}}}$

Этот метод согласуется с определенным интегралом, вычисленным более механическими способами:

${\ displaystyle \ int _ {0} ^ {2} x ^ {2} \, dx = {\ frac {8} {3}}}$

Поскольку функция является непрерывной и монотонно возрастающей на интервале, правая сумма Римана завышает интеграл на наибольшую величину (в то время как левая сумма Римана занижает интеграл на наибольшую величину). Этот факт, который интуитивно понятен из диаграмм, показывает, как характер функции определяет, насколько точно оценивается интеграл. Хотя простые, правые и левые суммы Римана часто менее точны, чем более продвинутые методы оценки интеграла, такие как правило трапеций или правило Симпсона.

В примере функции есть простая для поиска антипроизводная, поэтому оценка интеграла с помощью сумм Римана в основном является академическим упражнением; однако следует помнить, что не все функции имеют антипроизводные, поэтому оценка их интегралов путем суммирования практически важна.

Основная идея, лежащая в основе суммы Римана, состоит в том, чтобы «разбить» область посредством разделения на части, умножить «размер» каждой части на некоторое значение, которое функция принимает для этой части, и просуммировать все эти продукты. Это можно обобщить, чтобы можно было использовать суммы Римана для функций в областях более чем одного измерения.

Хотя интуитивно процесс разделения домена прост для понимания, технические детали того, как домен может быть разделен, становятся намного сложнее, чем в одномерном случае, и включают аспекты геометрической формы домена.

Два измерения

В двух измерениях домен можно разделить на несколько ячеек, например. В двух измерениях каждая ячейка может быть интерпретирована как имеющая «область», обозначенную значком. Сумма Римана равна ${\ displaystyle A}$${\ displaystyle A_ {i}}$${\ textstyle A = \ bigcup _ {i} A_ {i}}$${\ displaystyle \ Delta A_ {i}}$

${\ displaystyle S = \ sum _ {i = 1} ^ {n} f (x_ {i} ^ {*}, y_ {i} ^ {*}) \, \ Delta A_ {i},}$

где. ${\ displaystyle (x_ {i} ^ {*}, y_ {i} ^ {*}) \ in A_ {i}}$

Три измерения

В трех измерениях обычно используется буква для домена, например, под разделом и это «объем» ячейки, проиндексированной. Тогда трехмерная сумма Римана может быть записана как ${\ displaystyle V}$${\ textstyle V = \ bigcup _ {i} V_ {i}}$${\ displaystyle \ Delta V_ {i}}$${\ displaystyle i}$

${\ displaystyle S = \ sum _ {i = 1} ^ {n} f (x_ {i} ^ {*}, y_ {i} ^ {*}, z_ {i} ^ {*}) \, \ Delta V_ {i}}$

с. ${\ displaystyle (x_ {i} ^ {*}, y_ {i} ^ {*}, z_ {i} ^ {*}) \ in V_ {i}}$

Произвольное количество измерений

Суммы Римана с более высокой размерностью следуют тому же принципу, что и от одного до двух или трех измерений. Для произвольной размерности n сумма Римана может быть записана как

${\ displaystyle S = \ sum _ {i} f (P_ {i} ^ {*}) \, \ Delta V_ {i}}$

где, то есть это точка в n-мерной ячейке с n-мерным объемом. ${\ displaystyle P_ {i} ^ {*} \ in V_ {i}}$${\ displaystyle V_ {i}}$${\ displaystyle \ Delta V_ {i}}$

Обобщение

В общих чертах суммы Римана можно записать

${\ Displaystyle S = \ сумма _ {я} f (P_ {i} ^ {*}) \ mu (V_ {i})}$

где обозначает любую произвольную точку, содержащуюся в элементе разбиения, и является мерой на нижележащем множестве. Грубо говоря, мера - это функция, которая дает «размер» набора, в данном случае размер набора ; в одном измерении это часто можно интерпретировать как длину интервала в двух измерениях, площадь, в трех измерениях, объем и т. д. ${\ displaystyle P_ {i} ^ {*}}$${\ displaystyle V_ {i}}$${\ displaystyle \ mu}$ ${\ displaystyle V_ {i}}$

• Первообразный
• Метод Эйлера и середины метод, родственные методы решения дифференциальных уравнений
• Интеграл Лебега
• Интеграл Римана, предел сумм Римана, когда разбиение становится бесконечно тонким
• Правило Симпсона, мощный численный метод, более мощный, чем простые суммы Римана или даже правило трапеций
• Правило трапеции, численный метод на основе среднего значения левой и правой суммы Римана

• Вайсштейн, Эрик В. «Риман Сумма». MathWorld.
• Моделирование, показывающее сходимость сумм Римана