Трапецеидальная линейка

Метод численного интегрирования Функция f (x) (синим цветом) аппроксимируется линейной функцией (красным цветом).

В математике, а точнее в численном анализе, правило трапеции (также известное как правило трапеций или правило трапеции ) - это метод аппроксимации определенного интеграла.

$\int \; abf\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\}$.

Правило трапеции работает путем аппроксимации области под графиком функции $f\; (x)\; \{\backslash \; displaystyle\; f\; (x)\}$как трапеции и вычисления ее площади. Отсюда следует, что

$\int \; abf\; (x)\; dx\; \approx \; (b\; -\; a)\; \cdot \; f\; (a)\; +\; f\; (b)\; 2\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; (ba)\; \backslash \; cdot\; \{\backslash \; tfrac\; \{f\; (a)\; +\; f\; (b)\}\; \{2\}\}\}$.

Правило трапеции можно рассматривать как результат, полученный путем усреднения левого и справа Риман суммирует, и иногда его определяют таким образом. Интеграл можно еще лучше аппроксимировать, разделив интервал интегрирования, применив правило трапеции к каждому подинтервалу и суммируя результаты. На практике это «сцепленное» (или «составное») правило трапеции обычно подразумевается под «интеграцией с правилом трапеции». Пусть $\{xk\}\; \{\backslash \; displaystyle\; \backslash \; \{x\_\; \{k\}\; \backslash \}\}$будет разделом $[a,\; b]\; \{\backslash \; displaystyle\; [a,\; b]\}$таким образом, что и $\Delta \; xk\; \{\backslash \; displaystyle\; \backslash \; Delta\; x\_\; \{k\}\}$быть длиной $k\; \{\backslash \; displaystyle\; k\}$-й подынтервал (то есть $\Delta \; xk\; =\; xk\; -\; xk\; -\; 1\; \{\backslash \; displaystyle\; \backslash \; Delta\; x\_\; \{k\}\; =\; x\_\; \{k\}\; -x\_\; \{k-1\}\}$), то

$\int \; abf\; (x)\; dx\; \approx \; \sum \; k\; =\; 1\; N\; f\; (xk\; -\; 1)\; +\; f\; (xk)\; 2\; \Delta \; xk\; =\; \Delta \; x\; 2\; (f\; (x\; 0)\; +\; 2\; f\; (Икс\; 1)\; +\; 2\; е\; (Икс\; 2)\; +\; 2\; е\; (Икс\; 3)\; +\; 2\; е\; (Икс\; 4)\; +\; \cdots \; +\; 2\; е\; (Икс\; N\; -\; 1)\; +\; е\; (Икс\; N))\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{\; a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{f\; (x\_\; \{k-1\})\; +\; f\; (x\_\; \{k\})\}\; \{\; 2\}\}\; \backslash \; Delta\; x\_\; \{k\}\; =\; \{\backslash \; tfrac\; \{\backslash \; Delta\; x\}\; \{2\}\}\; \backslash \; left\; (f\; (x\_\; \{0\})\; +\; 2f\; (x\_\; \{1\})\; +\; 2f\; (x\_\; \{2\})\; +\; 2f\; (x\_\; \{3\})\; +\; 2f\; (x\_\; \{4\})\; +\; \backslash \; cdots\; +\; 2f\; (x\_\; \{N-1\})\; +\; f\; (x\_\; \{N\})\; \backslash \; right)\}$.

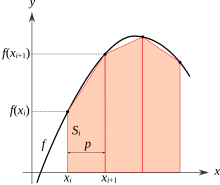
Анимация, показывающая правило трапеции есть и как ошибка аппроксимации уменьшается по мере уменьшения размера шага Иллюстрация «цепной трапециевидной линейки», используемой на неравномерно разнесенном разделе $[\; a,\; b]\; \{\backslash \; displaystyle\; [a,\; b]\}$.

Приближение становится более точным по мере увеличения разрешения раздела (то есть для больших $N\; \{\backslash \; displaystyle\; N\}$, $\Delta \; xk\; \{\backslash \; displaystyle\; \backslash \; Delta\; x\_\; \{k\}\}$уменьшается). Когда разделение имеет постоянный интервал, как это часто бывает, формулу можно упростить для повышения эффективности вычислений.

Как обсуждается ниже, также возможно установить границы погрешности для точности значения определенного интеграла, оцененного с использованием правила трапеций.

• 1 История
• 2 Численная реализация
  • 2.1 Неравномерная сетка
  • 2.2 Однородная сетка
• 3 Анализ ошибок
  • 3.1 Доказательство
  • 3.2 Периодические и пиковые функции
  • 3.3 «Грубые» функции
• 4 Применимость и альтернативы
• 5 См. Также
• 6 Примечания
• 7 Ссылки
• 8 Внешние ссылки

В документе 2016 года сообщается, что правило трапеции использовалось в Вавилоне до 50 г. до н.э. для интегрирования скорости Юпитера вдоль эклиптики.

Неравномерная сетка

Когда шаг сетки неравномерен, можно использовать формулу

$\int \; abf\; (x)\; dx\; \approx \; \sum \; k\; =\; 1\; N\; f\; (xk\; -\; 1)\; +\; f\; (xk)\; 2\; \Delta \; xk\; \{\; \backslash \; Displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{f\; (x\_\; \{k-1\})\; +\; f\; (x\_\; \{k\})\}\; \{2\}\}\; \backslash \; Delta\; x\_\; \{k\}\}$

Равномерная сетка

Для домена, дискретизированного на $N\; \{\backslash \; displaystyle\; N\}$панели с одинаковым интервалом, может произойти значительное упрощение. Пусть

$\Delta \; xk\; =\; \Delta \; x\; =\; b\; -\; a\; N\; \{\backslash \; displaystyle\; \backslash \; Delta\; x\_\; \{k\}\; =\; \backslash \; Delta\; x\; =\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\}$

, приближение к интегралу становится

$\int \; abf\; (Икс)\; dx\; \approx \; \Delta \; Икс\; 2\; \sum \; К\; знак\; равно\; 1\; N\; (е\; (xk\; -\; 1)\; +\; f\; (xk))\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; Delta\; x\}\; \{2\}\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \backslash \; left\; (f\; (x\_\; \{k-1\})\; +\; f\; (x\_\; \{k\})\; \backslash \; right)\}$

$=\; \Delta \; x\; 2\; (f\; (x\; 0)\; +\; 2\; f\; (x\; 1)\; +\; 2\; f\; (x\; 2)\; +\; 2\; f\; (x\; 3)\; +\; \cdots \; +\; 2\; f\; (x\; N\; -\; 1)\; +\; f\; (x\; N)).)\; \{\backslash \; displaystyle\; \{\}\; =\; \{\backslash \; frac\; \{\backslash \; Delta\; x\}\; \{2\}\}\; (f\; (x\_\; \{0\})\; +\; 2f\; (x\_\; \{1\})\; +\; 2f\; (x\_\; \{2\})\; +\; 2f\; (x\_\; \{3\}))\; +\; \backslash \; dotsb\; +\; 2f\; (x\_\; \{N-1\})\; +\; f\; (x\_\; \{N\}))\}$

$=\; \Delta \; x\; 2\; (f\; (x\; 0)\; +\; f\; (x\; N)\; +\; 2\; \sum \; k\; =\; 1\; N\; -\; 1\; е\; (xk))\; \{\backslash \; displaystyle\; \{\}\; =\; \{\backslash \; frac\; \{\backslash \; Delta\; x\}\; \{2\}\}\; \backslash \; left\; (f\; (x\_\; \{0\})\; +\; f\; (x\_\; \{N\})\; +\; 2\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N-1\}\; f\; (x\_\; \{k\})\; \backslash \; right)\}$

$=\; \Delta \; x\; (\sum \; k\; =\; 1\; N\; -\; 1\; f\; (xk)\; +\; f\; (x\; N)\; +\; f\; (x\; 0)\; 2)\; \{\backslash \; displaystyle\; \{\}\; =\; \backslash \; Delta\; x\; \backslash \; left\; (\backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N-1\}\; f\; (x\_\; \{k\})\; +\; \{\backslash \; frac\; \{f\; (x\_\; \{N\})\; +\; f\; (\; x\_\; \{0\})\}\; \{2\}\}\; \backslash \; right)\}$

, что требует меньшего количества вычислений функции для вычисления.

Анимация, показывающая, как улучшается аппроксимация трапециевидного правила с увеличением количества полос для интервала с $a\; =\; 2\; \{\backslash \; displaystyle\; a\; =\; 2\}$и $б\; =\; 8\; \{\backslash \; Displaystyle\; b\; =\; 8\}$. По мере увеличения количества интервалов $N\; \{\backslash \; displaystyle\; N\}$увеличивается и точность результата.

Ошибка составной трапециевидной линейки - это разница между значением интеграла и числовой результат:

$error\; =\; \int \; abf\; (x)\; dx\; -\; b\; -\; a\; N\; [f\; (a)\; +\; f\; (b)\; 2\; +\; \sum \; k\; =\; 1\; N\; -\; 1\; f\; (a\; +\; kb\; -\; a\; N)]\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{error\}\}\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; -\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; left\; [\{f\; (a)\; +\; f\; (\; б)\; \backslash \; over\; 2\}\; +\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N-1\}\; f\; \backslash \; left\; (a\; +\; k\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; right)\; \backslash \; right]\}$

Существует число ξ между a и b, такое, что

$error\; =\; -\; (b\; -\; a)\; 3\; 12\; N\; 2\; f\; ″\; (\xi )\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{error\}\}\; =\; -\; \{\backslash \; frac\; \{(ba)\; ^\; \{3\}\}\; \{12N\; ^\; \{2\}\}\}\; f\; \text{'}\text{'}\; (\backslash \; xi)\}$

Отсюда следует, что если подынтегральное выражение вогнуто вверх (и, следовательно, имеет положительную вторую производную), то ошибка отрицательная, и правило трапеции переоценивает истинное значение. Это также видно из геометрической картины: трапеции охватывают всю область под кривой и проходят над ней. Аналогично, функция вогнутая вниз дает заниженную оценку, поскольку площадь под кривой не учитывается, но не учитывается выше. Если интервал аппроксимируемого интеграла включает точку перегиба, ошибку выявить труднее.

Асимптотическая оценка ошибки при N → ∞ дается как

$error\; =\; -\; (b\; -\; a)\; 2\; 12\; N\; 2\; [f\; \prime \; (b)\; -\; f\; \prime \; (a)]\; +\; O\; (N\; -\; 3).\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{error\}\}\; =\; -\; \{\backslash \; frac\; \{(ba)\; ^\; \{2\}\}\; \{12N\; ^\; \{2\}\}\}\; \{\backslash \; big\; [\}\; f\; \text{'}(b)\; -f\text{'}\; (a)\; \{\backslash \; big]\}\; +\; O\; (N\; ^\; \{-\; 3\}).\}$

Дополнительные члены в этой оценке погрешности даются формулой суммирования Эйлера – Маклорена.

Для анализа ошибки можно использовать несколько методов, в том числе:

1. ряд Фурье
2. Исчисление остатков
3. Формула суммирования Эйлера – Маклорена
4. Полиномиальная интерполяция

. Утверждается, что скорость сходимости трапецеидального правила отражает и может использоваться в качестве определения классов гладкости функций.

Доказательство

Сначала предположим, что $h\; =\; b\; -\; a\; N\; \{\backslash \; displaystyle\; h\; =\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\}$и $ak\; =\; a\; +\; (k\; -\; 1)\; h\; \{\backslash \; displaystyle\; a\_\; \{k\}\; =\; a\; +\; (k-1)\; h\}$. Пусть $gk\; (t)\; =\; 1\; 2\; t\; [f\; (ak)\; +\; f\; (ak\; +\; t)]\; -\; \int \; akak\; +\; tf\; (x)\; dx\; \{\backslash \; displaystyle\; g\_\; \{k\}\; (t)\; =\; \{\backslash \; frac\; \{1\; \}\; \{2\}\}\; t\; [f\; (a\_\; \{k\})\; +\; f\; (a\_\; \{k\}\; +\; t)]\; -\; \backslash \; int\; \_\; \{a\_\; \{k\}\}\; ^\; \{a\_\; \{k\}\; +\; t\}\; f\; (x)\; dx\}$- функция, такая что $|\; g\; k\; (h)\; |\; \{\backslash \; displaystyle\; |\; g\_\; \{k\}\; (h)\; |\}$- ошибка правила трапеции на одном из интервалов, $[ak,\; ak\; +\; h]\; \{\backslash \; displaystyle\; [a\_\; \{k\},\; а\_\; \{k\}\; +\; h]\}$. Тогда

$dgkdt\; =\; 1\; 2\; [f\; (ak)\; +\; f\; (ak\; +\; t)]\; +\; 1\; 2\; t\; \cdot \; f\; \prime \; (ak\; +\; t)\; -\; f\; (ak\; +\; t),\; \{\backslash \; displaystyle\; \{dg\_\; \{k\}\; \backslash \; над\; dt\}\; =\; \{1\; \backslash \; над\; 2\}\; [f\; (a\_\; \{k\})\; +\; f\; (a\_\; \{k\}\; +\; t)]\; +\; \{1\; \backslash \; over\; 2\}\; t\; \backslash \; cdot\; f\; \text{'}(a\_\; \{k\}\; +\; t)\; -\; f\; (a\_\; \{k\}\; +\; t),\}$

и

$d\; 2\; gkdt\; 2\; =\; 1\; 2\; t\; \cdot \; f\; ″\; (ak\; +\; t).\; \{\backslash \; displaystyle\; \{d\; ^\; \{2\}\; g\_\; \{k\}\; \backslash \; over\; dt\; ^\; \{2\}\}\; =\; \{1\; \backslash \; over\; 2\}\; t\; \backslash \; cdot\; f\; \text{'}\text{'}\; (a\_\; \{k\}\; +\; t).\}$

Теперь предположим, что $|\; f\; ″\; (x)\; |\; \le \; е\; ″\; (\xi ),\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; vert\; f\; \text{'}\text{'}\; (x)\; \backslash \; right\; \backslash \; vert\; \backslash \; leq\; f\; \text{'}\text{'}\; (\backslash \; xi),\}$который выполняется, если $f\; \{\backslash \; displaystyle\; f\}$достаточно гладкий. Отсюда следует, что

$|\; f\; ″\; (a\; k\; +\; t)\; |\; \le \; е\; ″\; (\xi )\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; vert\; f\; \text{'}\text{'}\; (a\_\; \{k\}\; +\; t)\; \backslash \; right\; \backslash \; vert\; \backslash \; leq\; f\; \text{'}\text{'}\; (\backslash \; xi)\}$

, что эквивалентно $-\; f\; ″\; (\Xi )\; \le \; е\; ″\; (ak\; +\; t)\; \le \; f\; ″\; (\xi )\; \{\backslash \; displaystyle\; -f\; \text{'}\text{'}\; (\backslash \; xi)\; \backslash \; leq\; f\; \text{'}\text{'}\; (a\_\; \{k\}\; +\; t)\; \backslash \; leq\; f\; \text{'}\text{'}\; (\backslash \; xi)\}$, или $-\; f\; ″\; (\xi )\; t\; 2\; \le \; gk\; ″\; (t)\; \le \; f\; ″\; (\xi )\; t\; 2.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; t\}\; \{2\}\}\; \backslash \; leq\; g\_\; \{k\}\; \text{'}\text{'}\; (t)\; \backslash \; leq\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; t\}\; \{2\}\; \}.\}$

Поскольку $gk\; \prime \; (0)\; =\; 0\; \{\backslash \; displaystyle\; g\_\; \{k\}\; \text{'}(0)\; =\; 0\}$и $gk\; (0)\; =\; 0\; \{\backslash \; displaystyle\; g\_\; \{k\}\; (0)\; =\; 0\}$,

$\int \; 0\; tgk\; ″\; (x)\; dx\; =\; gk\; \prime \; (t)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{t\}\; g\_\; \{k\}\; \text{'}\text{'}\; (x)\; dx\; =\; g\_\; \{k\}\; \text{'}(t)\}$и $\int \; 0\; tgk\; \prime \; (x)\; dx\; =\; gk\; (t).\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{t\}\; g\_\; \{k\}\; \text{'}(x)\; dx\; =\; g\_\; \{k\}\; (t).\}$

Используя эти результаты, находим

$-\; f\; ″\; (\xi )\; t\; 2\; 4\; \le \; gk\; \prime \; (t)\; \le \; f\; ″\; (\xi )\; t\; 2\; 4\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; t\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; leq\; g\_\; \{k\}\; \text{'}\; (t)\; \backslash \; leq\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; t\; ^\; \{2\}\}\; \{4\}\}\}$

и

$-\; f\; ″\; (\xi )\; t\; 3\; 12\; \le \; gk\; (t)\; \le \; f\; ″\; (\Xi )\; t\; 3\; 12\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; t\; ^\; \{3\}\}\; \{12\}\}\; \backslash \; leq\; g\_\; \{k\}\; (t)\; \backslash \; leq\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; t\; ^\; \{3\}\}\; \{12\}\}\}$

Полагая $t\; =\; h\; \{\backslash \; displaystyle\; t\; =\; h\}$, мы находим

$-\; f\; ″\; (\xi )\; h\; 3\; 12\; \le \; gk\; (h)\; \le \; f\; ″\; (\xi )\; h\; 3\; 12.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{3\}\}\; \{12\}\}\; \backslash \; leq\; g\_\; \{k\}\; (h)\; \backslash \; leq\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{\; 3\}\}\; \{12\}\}.\}$

Суммируя все члены локальной ошибки, мы находим

$\sum \; k\; =\; 1\; N\; gk\; (h)\; =\; b\; -\; a\; N\; [f\; (a)\; +\; f\; (b)\; 2\; +\; K\; =\; 1\; N\; -\; 1\; f\; (a\; +\; kb\; -\; a\; N)]\; -\; \int \; abf\; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; g\_\; \{k\}\; (h)\; =\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; left\; [\{f\; (a)\; +\; f\; (b)\; \backslash \; over\; 2\}\; +\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N-1\}\; f\; \backslash \; left\; (a\; +\; k\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; right)\; \backslash \; right]\; -\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; dx.\}$

Но мы также имеем

$-\; \sum \; k\; =\; 1\; N\; f\; ″\; (\xi )\; h\; 3\; 12\; \le \; \sum \; k\; =\; 1\; N\; gk\; (h)\; \le \; \sum \; k\; =\; 1\; N\; f\; ″\; (\xi )\; час\; 3\; 12\; \{\backslash \; displaystyle\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{3\}\}\; \{12\}\}\; \backslash \; leq\; \backslash \; sum\; \_\; \{k\; =\; 1\; \}\; ^\; \{N\}\; g\_\; \{k\}\; (h)\; \backslash \; leq\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{3\}\}\; \{12\}\}\}$

и

$\sum \; k\; =\; 1\; N\; f\; ″\; (\xi )\; h\; 3\; 12\; =\; f\; ″\; (\xi )\; h\; 3\; N\; 12,\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{f\; \text{'}\; \text{'}(\backslash \; xi)\; h\; ^\; \{3\}\}\; \{12\}\}\; =\; \{\backslash \; frac\; \{f\text{'}\; \text{'}(\backslash \; xi)\; h\; ^\; \{3\}\; N\}\; \{12\}\},\}$

так что

$-\; f\; ″\; (\Xi )\; h\; 3\; N\; 12\; \le \; b\; -\; a\; N\; [f\; (a)\; +\; f\; (b)\; 2\; +\; \sum \; k\; =\; 1\; N\; -\; 1\; f\; (a\; +\; kb\; -\; a\; N)]\; -\; \int \; abf\; (x)\; dx\; \le \; f\; ″\; (\xi )\; h\; 3\; N\; 12.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{3\}\; N\}\; \{12\}\}\; \backslash \; leq\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; left\; [\{f\; (a)\; +\; f\; (b)\; \backslash \; over\; 2\}\; +\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N-1\}\; f\; \backslash \; left\; (a\; +\; k\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; right)\; \backslash \; right]\; -\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; dx\; \backslash \; leq\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{3\}\; N\}\; \{12\}\}.\}$

Следовательно, общая ошибка ограничена величиной

$error\; =\; \int \; abf\; (x)\; dx\; -\; b\; -\; a\; N\; [f\; (a)\; +\; f\; (b)\; 2\; +\; \sum \; k\; =\; 1\; N\; -\; 1\; f\; (a\; +\; kb\; -\; a\; N)]\; =\; f\; ″\; (\xi )\; h\; 3\; N\; 12\; =\; f\; ″\; (\xi )\; (б\; -\; а)\; 3\; 12\; N\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{error\}\}\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; dx\; -\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; left\; [\{f\; (a)\; +\; f\; (b)\; \backslash \; over\; 2\}\; +\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N-1\}\; f\; \backslash \; left\; (a\; +\; k\; \{\backslash \; frac\; \{ba\}\; \{N\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; h\; ^\; \{3\}\; N\}\; \{12\}\}\; =\; \{\backslash \; frac\; \{f\; \text{'}\text{'}\; (\backslash \; xi)\; (ba)\; ^\; \{3\}\}\; \{12N\; ^\; \{2\}\}\}.\}$

Периодические и пиковые функции

Правило трапеции быстро сходится для периодических функций. Это простое следствие формулы суммирования Эйлера-Маклорена, которая гласит, что если $f\; \{\backslash \; displaystyle\; f\}$равно $p\; \{\backslash \; displaystyle\; p\}$раз непрерывно дифференцируемые с периодом $T\; \{\backslash \; displaystyle\; T\}$

$\sum \; k\; =\; 0\; N\; -\; 1\; f\; (kh)\; h\; =\; \int \; 0\; T\; f\; (x)\; dx\; +\; \sum \; k\; =\; 1\; \lfloor \; p\; /\; 2\; \rfloor \; B\; 2\; k\; (\; 2\; к)!\; (е\; (2\; К\; -\; 1)\; (Т)\; -\; е\; (2\; К\; -\; 1)\; (0))\; -\; (-\; 1)\; php\; \int \; 0\; ТБ\; ~\; p\; (x\; /\; T)\; f\; (p)\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{N-1\}\; f\; (kh)\; h\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{T\}\; f\; (x)\; \backslash ,\; dx\; +\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; lfloor\; p\; /\; 2\; \backslash \; rfloor\}\; \{\backslash \; frac\; \{B\_\; \{2k\}\}\; \{(2k)!\}\}\; (F\; ^\; \{(2k-1)\}\; (T)\; -f\; ^\; \{(2k-1)\}\; (0))\; -\; (\; -1)\; ^\; \{p\}\; h\; ^\; \{p\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{T\}\; \{\backslash \; tilde\; \{B\}\}\; \_\; \{p\}\; (x\; /\; T)\; f\; ^\; \{(p)\}\; (x)\; \backslash ,\; \backslash \; mathrm\; \{d\}\; x\}$

где $h:\; =\; T\; /\; N\; \{\backslash \; displaystyle\; h:\; =\; T\; /\; N\}$и $B\; ~\; p\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\; B\}\}\; \_\; \{p\}\}$- периодическое расширение $p\; \{\backslash \; displaystyle\; p\}$-го многочлена Бернулли. Из-за периодичности производные в конечной точке отменяются, и мы видим, что ошибка составляет $O\; (hp)\; \{\backslash \; displaystyle\; O\; (h\; ^\; \{p\})\}$.

Аналогичный эффект доступен для функций типа пика., такие как Гауссов, Экспоненциально модифицированный Гауссов и другие функции с производными в пределах интегрирования, которыми можно пренебречь. Оценка полного интеграла функции Гаусса по правилу трапеций с точностью 1% может быть произведена с использованием всего 4 точек. Правило Симпсона требует в 1,8 раза больше точек для достижения той же точности.

Хотя были предприняты некоторые усилия по распространению формулы суммирования Эйлера-Маклорена на более высокие измерения, наиболее прямым доказательством быстрой сходимости правила трапеций в высших измерениях является сведение проблемы к проблеме сходимости рядов Фурье. Это рассуждение показывает, что если $f\; \{\backslash \; displaystyle\; f\}$периодичен в $n\; \{\backslash \; displaystyle\; n\}$-мерном пространстве с $p\; \{\; \backslash \; displaystyle\; p\}$непрерывные производные, скорость сходимости равна $O\; (hp\; /\; d)\; \{\backslash \; displaystyle\; O\; (h\; ^\; \{p\; /\; d\})\}$. Для очень большого измерения результаты показывают, что интеграция методом Монте-Карло, скорее всего, является лучшим выбором, но для 2-х и 3-х измерений эффективна равномерная выборка. Это используется в вычислительной физике твердого тела, где равномерная выборка по примитивным ячейкам в обратной решетке известна как интеграция Монкхорста-Пак.

«Грубые» функции

Для функций, которых нет в C, граница ошибки, указанная выше, не применима. Тем не менее, границы ошибок для таких грубых функций могут быть получены, которые обычно показывают более медленную сходимость с количеством вычислений функции $N\; \{\backslash \; displaystyle\; N\}$, чем $O\; (N\; -\; 2)\; \{\backslash \; displaystyle\; O\; (N\; ^\; \{-\; 2\})\}$поведение, указанное выше. Интересно, что в этом случае правило трапеции часто имеет более точные границы, чем правило Симпсона для того же количества вычислений функции.

Правило трапеции является одним из семейство формул для численного интегрирования, называемое формулами Ньютона – Котеса, из которых правило средней точки аналогично правилу трапеций. Правило Симпсона является другим членом того же семейства и в целом имеет более быструю сходимость, чем правило трапеций, для функций, которые дважды непрерывно дифференцируемы, хотя и не во всех конкретных случаях. Однако для различных классов более грубых функций (с более слабыми условиями гладкости) правило трапеций имеет более быструю сходимость, чем правило Симпсона.

Более того, правило трапеций имеет тенденцию становиться чрезвычайно точным, когда периодические функции интегрированы по своим периодам, которые могут быть проанализированы различными способами. Аналогичный эффект доступен для функций пика.

Однако для непериодических функций методы с неравномерно разнесенными точками, такие как квадратурная формула Гаусса и квадратура Кленшоу – Кертиса, являются как правило, гораздо точнее; Квадратуру Кленшоу – Кертиса можно рассматривать как замену переменных для выражения произвольных интегралов в терминах периодических интегралов, при этом правило трапеций может применяться точно.

• Квадратура Гаусса
• Формулы Ньютона – Котеса
• Метод прямоугольников
• Метод Ромберга
• Правило Симпсона
• Интегральное уравнение Вольтерра # Численное решение с использованием правила трапеции

1. ^Оссендрейвер, Матье (29 января 2016 г.). «Древние вавилонские астрономы вычислили положение Юпитера на основе графика времени-скорости». Наука. 351 (6272): 482–484. doi : 10.1126 / science.aad8085. PMID 26823423. S2CID 206644971.
2. ^Аткинсон (1989, уравнение (5.1.7))
3. ^(Weideman 2002, стр. 23, раздел 2)
4. ^Аткинсон (1989, уравнение (5.1.9))
5. ^Аткинсон (1989, стр. 285)
6. ^Burden Faires (2011, стр. 194) harvtxt error: no target: CITEREFBurdenFaires2011 (help )
7. ^ (Rahman Schmeisser 1990)
8. ^Kress, Rainer (1998). Numerical Analysis, volume 181 of Graduate Texts in Mathematics. Springer-Verlag.
9. ^Goodwin, ET (1949). «Вычисление интегралов формы». Mathematical Proceedings of the Cambridge Philosophical Society. 45 (2): 241–245. doi : 10.1017 / S0305004100024786. ISSN 1469-8064.
10. ^ Каламбет, Юрий; Козьмин, Юрий; Самохин, Андрей (2018). «Сравнение правил интегрирования в случае очень узкой хроматографии. пики ». Хемометрия и интеллектуальные лабораторные системы. 179 : 22–30. doi : 10.1016 / j.chemolab.2018.06.001. ISSN 0169-7439.
11. ^ (Weideman 2002)
12. ^«Формула суммирования Эйлера-Маклорена для множественных сумм». Math.stackexchange.com.
13. ^Томпсон, Ник. » Численное интегрирование по зонам Бриллюэна ". bandgap.io. Проверено 19 декабря 2017 г.
14. ^ (Cruz-Uribe Neugebauer 2002)

Викиучебник Математика A-level имеет страницу по теме: Правило трапеции

• , Энциклопедия математики, изд. М. Хазевинкель
• Заметки о сходимости квадратуры трапеции
• Реализация квадратуры трапеции, предоставленная Boost.Math