Угловой диаметр

редактировать

Угловой диаметр, угловой размер, кажущийся диаметр, или кажущийся размер - угловое измерение, описывающее, насколько большой сфера или круг выглядит с данной точки зрения. В науках о зрении это называется углом обзора, а в оптике это угловая апертура (из объектив ). В качестве альтернативы угловой диаметр можно рассматривать как угол, на который глаз или камера должны повернуться, чтобы смотреть с одной стороны видимого круга на противоположную. Угловой радиус равен половине углового диаметра.

Содержание

1 Формула
2 Оценка углового диаметра с помощью руки
3 Использование в астрономии
- 3.1 Некруглые объекты
- 3.2 Дефект освещения
4 См. Также
5 Ссылки
6 Внешние ссылки

Формула

Диаграмма для формулы углового диаметра

Угловой диаметр окружности, плоскость которой перпендикулярна вектору смещения между точкой вид и центр указанного круга можно рассчитать по формуле

δ = 2 arctan ⁡ (d 2 D), {\ displaystyle \ delta = 2 \ arctan \ left ({\ frac {d} {2D}} \ справа),}

\ delta = 2 \ arctan \ left ({\ frac {d} {2D}} \ right),

, где $δ {\ displaystyle \ delta}$ $\ delta$ - угловой диаметр, а $d {\ displaystyle d}$ $d$ - фактический диаметр объекта, а $D {\ displaystyle D}$ $D$ - расстояние до объекта. Когда $D ≫ d {\ displaystyle D \ gg d}$ $D \ gg d$ , мы имеем $δ ≈ d / D {\ displaystyle \ delta \ приблизительно d / D}$ $\ delta \ приблизительно d / D$ , и полученный результат выражен в радианах.

. Для сферического объекта, фактический диаметр которого равен $dact, {\ displaystyle d _ {\ mathrm {act}},}$ $d _ {\ mathrm {act}},$ и где $D {\ displaystyle D}$ $D$ - расстояние до центра сферы, угловой диаметр можно найти по формуле

δ = 2 arcsin ⁡ (dact 2 D) {\ displaystyle \ delta = 2 \ arcsin \ left ({\ frac {d _ {\ mathrm {act}}} {2D}} \ right)}

\ delta = 2 \ arcsin \ left ({\ frac {d _ {\ mathrm {act}}} {2D}} \ right)

Разница в том, что видимые края сферы являются точками касания, которые находятся ближе к наблюдателю, чем к центру сферы. Для практического использования различие имеет значение только для сферических объектов, которые находятся относительно близко, поскольку приближение малых углов справедливо для $x ≪ 1 {\ displaystyle x \ ll 1}$ $x \ ll 1$ :

arcsin ⁡ x ≈ arctan ⁡ x ≈ x {\ displaystyle \ arcsin x \ приблизительно \ arctan x \ приблизительно x}

\ arcsin x \ приблизительно \ arctan x \ приблизительно x

Оценка углового диаметра с помощью руки

Приблизительные углы 10 °, 20 °, 5 ° и 1 ° для длина вытянутой руки.

Оценки углового диаметра могут быть получены, если держать руку под прямым углом к полностью вытянутой руке, как показано на рисунке.

Использование в астрономии

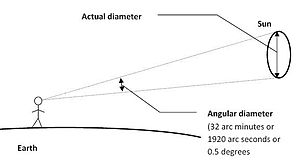Угловой диаметр: угол, образуемый объектом

В астрономии размеры небесных объектов часто задаются в терминах их углового диаметра, как видно из Земля, а не их реальные размеры. Поскольку эти угловые диаметры обычно малы, их принято представлять в угловых секундах (″). Угловая секунда равна 1/3600 одной градуса (1 °), а радиан - 180 / $π {\ displaystyle \ pi}$ $\ pi$ градусов. Таким образом, один радиан равен 3600 * 180 / $π {\ displaystyle \ pi}$ $\ pi$ arcseconds, что составляет около 206 265 угловых секунд (1 рад ≈ 206 264,806247 дюймов). Следовательно, угловой диаметр объекта с физическим диаметром d на расстоянии D, выраженное в секундах дуги, определяется как:

δ = 206, 265 (d / D) arcseconds {\ displaystyle \ delta = 206,265 ~ (d / D) ~ \ mathrm {arcseconds}}

{\ displaystyle \ delta = 206,265 ~ (d / D) ~ \ mathrm {arcseconds}}

Эти объекты имеют угловой диаметр 1 ″:

объект диаметром 1 см на расстоянии 2,06 км
объект диаметром 725,27 км на расстоянии 1 астрономическая единица (AU)
объект диаметром 45 866 916 км на расстоянии 1 светового года
объект диаметром 1 AU (149 597 871 км) на расстоянии 1 парсек (пк)

Таким образом, угловой диаметр орбиты Земли вокруг Солнца, если смотреть с расстояния в 1 пк, равен 2 ″, поскольку 1 а.е. радиус орбиты Земли.

Угловой диаметр Солнца с расстояния в один световой год составляет 0,03 ″, а диаметр Ea rth 0,0003 ″. Угловой диаметр Солнца 0,03 дюйма, указанный выше, примерно такой же, как у человеческого тела на расстоянии диаметра Земли.

В этой таблице показаны угловые размеры примечательных небесных тел как видно с Земли:

Небесное тело	Угловой диаметр или размер	Относительный размер
Галактика Андромеды	3 ° 10 ′ на 1 °	Примерно в шесть раз больше Солнца или Луны. Без фотографии с большой выдержкой.
Солнце	31′27 ″ - 32′32 ″	в 30–31 раз больше максимального значения для Венеры (внизу) / 1887–1952 ″
Луна	29′20 ″ - 34′6 ″	в 28–32,5 раза больше максимального значения для Венеры (оранжевая полоса внизу) / 1760–2046 ″
Туманность Хеликс	примерно 16 'на 28'
Шпиль в туманности Орла	4'40 ″	длина 280 ″
Венера	9,7 ″ - 1 ′ 6 ″
Юпитер	29,8 ″ - 50,1 ″
Сатурн	14,5 ″ - 20,1 ″
Марс	3,5 ″ - 25,1 ″
Меркурий	4,5 ″ - 13,0 ″
Уран	3,3–4,1 дюйма
Нептун	2,2–2,4 дюйма
Церера	0,33–0,84 дюйма
Веста	0,20–0,64 дюйма
Плутон	0,06 ″ - 0,11 ″
R Doradus	0,052 ″ - 0,062 ″
Бетельгейзе	0,049 ″ - 0,060 ″
Эрис	0,034 ″ - 0,089 ″
Alphard	0,00909 ″
Альфа Центавра A	0,007 ″
Канопус	0,006 ″
Сириус	0,005936 ″
Альтаир	0,003 ″
Денеб	0,002 ″
Проксима Центавра	0,001 ″
Алнитак	0,000 5 ″
Горизонт событий черной дыры M87 * в центре галактики M87, полученный телескопом Event Horizon Telescope в 2019 году.	0,000025 ″ (2,5 × 10)
Звезда, подобная Альнитак, на таком расстоянии, на котором космический телескоп Хаббл сможет ее увидеть	6 × 10 угловых секунд

Сравнение углового диаметра Солнца, Луны и планет. Чтобы получить точное представление о размерах, просмотрите изображение с расстояния, в 103 раза превышающего ширину "Луны: макс." круг. Например, если на вашем мониторе ширина этого круга составляет 5 см, просматривайте его с расстояния 5,15 м.

На этой фотографии сравниваются видимые размеры Юпитера и его четырех галилеевых спутников ( Каллисто при максимальном удлинении ) с видимым диаметром полной Луны во время их соединения 10 апреля 2017 года.

Таблица показывает, что угловой диаметр Солнца, если смотреть с Земли, составляет приблизительно 32 '(1920 ″ или 0,53 °), как показано выше.

Таким образом, угловой диаметр Солнца примерно в 250 000 раз больше, чем у Сириуса. (Сириус имеет вдвое больший диаметр, а расстояние до него в 500000 раз больше; Солнце в 10 раз ярче, что соответствует соотношению угловых диаметров 10, поэтому Сириус примерно в 6 раз ярче на единицу телесного угла.)

Угловой диаметр Солнца также примерно в 250 000 раз больше, чем у Альфа Центавра A (у него примерно такой же диаметр, а расстояние в 250 000 раз больше; Солнце 4 В 10 раз ярче, что соответствует соотношению угловых диаметров 200000, поэтому Альфа Центавра A немного ярче на единицу телесного угла).

Угловой диаметр Солнца примерно такой же, как у Луны. (Диаметр Солнца в 400 раз больше, равно как и расстояние до него; Солнце в 200000-500000 раз ярче полной Луны (цифры меняются), что соответствует отношению углового диаметра от 450 до 700, то есть небесное тело с диаметром 2,5–4 ″ и такой же яркости на единицу телесного угла будет иметь такую же яркость, как полная Луна.)

Даже несмотря на то, что Плутон физически больше Цереры, если смотреть с Земли (например, через Космический телескоп Хаббла ) Церера имеет гораздо больший видимый размер.

Угловые размеры, измеряемые в градусах, полезны для больших участков неба. (Например, три звезды Пояса покрывают угловой размер около 4,5 °.) Однако для измерения угловых размеров галактик, туманностей или других объектов требуются гораздо более точные единицы измерения. ночное небо.

Следовательно, градусы подразделяются следующим образом:

360 градусов (°) по полному кругу
60 угловые минуты (′) в один градус
60 угловых секунд (″) за одну угловую минуту

Чтобы представить это в перспективе, полная Луна, если смотреть с Земли составляет около ⁄ 2 °, или 30 '(или 1800 ″). Движение Луны по небу можно измерить по угловому размеру: примерно 15 ° каждый час или 15 дюймов в секунду. Линия длиной в одну милю, нарисованная на лице Луны, будет казаться с Земли примерно 1 дюйм в длину.

Минимальное, среднее и максимальное расстояние от Луны до Земли с учетом ее углового диаметра, если смотреть с поверхности Земли, в масштабе

В астрономии обычно трудно напрямую измерить расстояние до объекта, но объект может иметь известный физический размер (возможно, он похож на более близкий объект с известным расстоянием) и измеримый угловой диаметр. В этом случае формулу углового диаметра можно инвертировать, чтобы получить расстояние по угловому диаметру до удаленных объектов как

d ≡ 2 D tan ⁡ (δ 2) {\ displaystyle d \ Equiv 2D \ tan \ left ({\ frac {\ delta} {2}} \ right)}

d \ Equiv 2D \ tan \ left ({\ frac {\ delta} {2}} \ right)

В неевклидовом пространстве, таком как наша расширяющаяся Вселенная, расстояние по угловому диаметру является лишь одним из нескольких определений расстояния, так что может быть разные «расстояния» до одного и того же объекта. См. Измерения расстояния (космология).

Некруглые объекты

Многие объекты глубокого космоса, такие как галактики и туманности кажутся некруглыми и, таким образом, обычно имеют две меры диаметра: большую ось и малую ось. Например, Малое Магелланово Облако имеет видимый диаметр 5 ° 20 ′ × 3 ° 5 ′.

Дефект освещения

Дефект освещения - максимальная угловая ширина неосвещенной части небесного тела, видимой данным наблюдателем. Например, если объект имеет диаметр 40 дюймов по дуге и освещен на 75%, дефект освещения составляет 10 дюймов.

См. Также

Ссылки

Внешние ссылки