Телесный угол

редактировать

Мера того, насколько большим объект кажется наблюдателю в данной точке трехмерного пространства

Телесный угол
Общие символы	Ω
Единица СИ	Стерадиан
Другие единицы	Квадратный градус
В Основные единицы СИ	м / м
Расширенный ?	Да
Интенсивный ?	No
Сохранение ?	No
Производные от. других величин	$Ω = A / r 2 {\ displaystyle \ Omega = A / r ^ {2}}$ ${\ displaystyle \ Omega = A / r ^ {2}}$
Размер	$1 {\ displaystyle 1}$ $1$

В геометрии телесный угол (символ: Ω) - это мера величины поля обзора с некоторой конкретной точки, в которой данный объект крышки. То есть это мера того, насколько большим объект кажется наблюдателю, смотрящему с этой точки. Точка, из которой рассматривается объект, называется вершиной телесного угла, и говорят, что объект расширяет свой телесный угол от этой точки.

В Международной системе единиц (СИ) телесный угол выражается в безразмерных единицах, называемых стерадиан (символ: SR). Один стерадиан соответствует одной единице площади на единичной сфере, окружающей вершину, поэтому объект, который блокирует все лучи от вершины, будет покрывать количество стерадианов, равное общей площади поверхности единичной сферы, $4 π {\ displaystyle 4 \ pi}$ $4 \ pi$ . Телесные углы также могут быть измерены в квадратах угловых единиц, таких как градусов, минуты и секунды.

Маленький объект поблизости может образовывать тот же телесный угол, что и более крупный объект дальше. Например, хотя Луна намного меньше Солнца, она также намного ближе к Земле. Действительно, если смотреть из любой точки на Земле, оба объекта имеют примерно одинаковый телесный угол и кажущийся размер. Это очевидно во время солнечного затмения.

Содержание

1 Определение и свойства
2 Практическое применение
3 Телесные углы для обычных объектов
- 3.1 Конус, сферическая крышка, полусфера
- 3.2 Тетраэдр
- 3.3 Пирамида
- 3.4 Прямоугольник широты и долготы
- 3.5 Солнце и Луна
4 Телесные углы в произвольных размерах
5 Ссылки
6 Дополнительная литература
7 Внешние ссылки

Определение и свойства

Телесный угол объекта в стерадианах равен площади сегмента единичной сферы с центром в вершине, который покрывает объект. Телесный угол в стерадианах равен площади сегмента единичной сферы точно так же, как плоский угол в радианах равен длине дуги единичной окружности ; следовательно, точно так же, как плоский угол в радианах - это отношение длины дуги окружности к ее радиусу, телесный угол в стерадианах - это следующее отношение:

Ω = A r 2 {\ displaystyle \ Omega = {\ frac {A} {r ^ {2}}}}

{\ displaystyle \ Omega = {\ frac {A} {r ^ {2}}}}

где A - площадь сферической поверхности, а r - радиус рассматриваемой сферы.

Телесные углы часто используются в астрономии, физике и, в частности, астрофизике. Телесный угол объекта, который находится очень далеко, примерно пропорционален отношению площади к квадрату расстояния. Здесь «площадь» означает площадь объекта при проецировании в направлении взгляда.

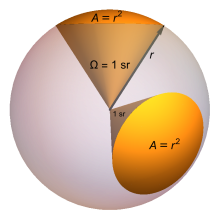
Любая область на сфере, площадь которой равна квадрату ее радиуса, если смотреть из ее центра, составляет ровно один стерадиан.

Телесный угол сферы, измеренный из любой точки внутри ее внутренней части, равен 4 π sr, а телесный угол, образуемый одной из его граней в центре куба, составляет одну шестую этого угла, или 2π / 3 sr. Телесные углы также могут быть измерены в квадратных градусах (1 sr = (180 / π) квадратных градусов), в квадратных минутах и квадратных секундах или в долях сферы (1 sr = 1 / 4π дробная площадь), также известный как spat (1 sp = 4π sr).

В сферических координатах есть формула для дифференциала,

d Ω = sin ⁡ θ d θ d φ {\ displaystyle d \ Omega = \ sin \ theta \, d \ theta \, d \ varphi}

d \ Omega = \ sin \ theta \, d \ theta \, d \ varphi

где θ - широта (угол от северного полюса), а φ - долгота.

Телесный угол для произвольной ориентированной поверхности S, обращенной в точку P, равен телесному углу проекции поверхности S на единичную сферу с центром P, который может быть вычисляется как интеграл поверхности :

Ω = ∬ S r ^ ⋅ n ^ d S r 2 = ∬ S sin ⁡ θ d θ d φ {\ displaystyle \ Omega = \ iint _ {S} {\ frac { {\ hat {r}} \ cdot {\ hat {n}} \, dS} {r ^ {2}}} \ = \ iint _ {S} \ sin \ theta \, d \ theta \, d \ varphi }

\ Omega = \ iint _ {S} {\ frac {{\ hat {r}} \ cdot {\ hat {n}} \, dS} {r ^ {2}}} \ = \ iint _ {S} \ sin \ theta \, d \ theta \, d \ varphi

где $r ^ = r → r {\ displaystyle {\ hat {r}} = {\ tfrac {\ vec {r}} {r}}}$ ${\ displaystyle {\ hat {r}} = {\ tfrac {\ vec {r}} { r}}}$ - это единичный вектор, соответствующий $r → {\ displaystyle {\ vec {r}}}$ ${\ vec {r}}$ , вектор положения бесконечно малой площади поверхности dS относительно точка P, и где $n ^ {\ displaystyle {\ hat {n}}}$ ${\ hat {n}}$ представляет единицу вектора нормали к dS. Даже если проекция единичной сферы на поверхность S не изоморфна, множественные складки правильно рассматриваются в соответствии с ориентацией поверхности, описываемой знаком скалярного произведения $r ^ ⋅ n ^ {\ displaystyle {\ hat {r}} \ cdot {\ hat {n}}}$ ${\ hat {r}} \ cdot {\ hat {n}}$ .

Таким образом, можно аппроксимировать телесный угол, образованный небольшой гранью с плоской поверхностью dS, ориентация $n ^ {\ displaystyle {\ hat {n}}}$ ${\ hat {n}}$ и расстояние r от зрителя как:

d Ω = 4 π (d SA) (r ^ ⋅ п ^) {\ displaystyle d \ Omega = 4 \ pi \ left ({\ frac {dS} {A}} \ right) \, ({\ hat {r}} \ cdot {\ hat {n}})}

{\ displaystyle d \ Omega = 4 \ pi \ left ({\ frac {dS} {A}} \ right) \, ({\ hat {r}} \ cdot {\ hat {n}) })}

, где площадь поверхности сферы равна A = 4πr.

Практическое применение

Определение силы света и яркости и соответствующих радиометрических величин интенсивности излучения и яркости
Расчет сферического избытка E сферического треугольника
Расчет потенциалов с использованием метода граничных элементов (БЭМ)
Оценка размера лиганды в металлических комплексах, см. угол конуса лиганда
Расчет электрического поля и напряженности магнитного поля вокруг зарядовых распределений
Получение Закон Гаусса
Расчет мощности излучения и излучения при теплопередаче
Расчет сечений в резерфордском рассеянии
Расчет сечений в комбинационном рассеянии
Телесный угол приемный конус оптического волокна

Телесные углы для обычных объектов

Конус, сферический колпачок, полусфера

Сечение конуса (1) и сферического колпачка (2) внутри сферы. На этом рисунке θ = A / 2 и r = 1.

Телесный угол конуса с вершиной на вершине телесного угла и с вершиной углом 2θ., это площадь сферической крышки на единичной сфере

Ω = 2 π (1 - cos ⁡ θ) = 4 π sin 2 ⁡ (θ 2) {\ displaystyle \ Omega = 2 \ pi \ left (1- \ cos {\ theta} \ right) \ = 4 \ pi \ sin ^ {2} \ left ({\ frac {\ theta} {2}} \ right) \}

{\ displaystyle \ Omega = 2 \ pi \ left (1- \ cos {\ theta} \ right) \ = 4 \ pi \ sin ^ {2} \ left ({\ frac {\ theta} {2}} \ right) \}

Для малых θ таких, что cos θ ≈ 1 - θ / 2, это сводится к площади круга πθ.

Вышеупомянутое находится путем вычисления следующего двойного интеграла с использованием единичного элемента поверхности в сферических координатах :

∫ 0 2 π ∫ 0 θ sin ⁡ θ ′ d θ ′ d ϕ знак равно 2 π ∫ 0 θ грех ⁡ θ ′ d θ ′ = 2 π [- cos ⁡ θ ′] 0 θ = 2 π (1 - cos ⁡ θ) {\ displaystyle \ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {\ theta} \ sin \ theta '\, d \ theta' \, d \ phi = 2 \ pi \ int _ {0} ^ {\ theta} \ sin \ theta '\, d \ theta '\ = 2 \ pi \ left [- \ cos \ theta' \ right] _ {0} ^ {\ theta} \ = 2 \ pi \ left (1- \ cos \ theta \ right) \}

\int _{0}^{2\pi }\int _{0}^{\theta }\sin \theta '\,d\theta '\,d\phi =2\pi \int _{0}^{\theta }\sin \theta '\,d\theta '\ =2\pi \left[-\cos \theta '\right]_{0}^{\theta }\ =2\pi \left(1-\cos \theta \right)\

Эту формулу можно также получить без использования исчисления. Более 2200 лет назад Архимед доказал, что площадь поверхности сферической шапки всегда равна площади круга, радиус которого равен расстоянию от края сферической шапки до точки, где находится ось симметрии крышки. пересекает шапку. На диаграмме этот радиус представлен как:

2 r sin ⁡ θ 2 {\ displaystyle 2r \ sin {\ frac {\ theta} {2}}}

{\ displaystyle 2r \ sin {\ frac {\ theta} {2}}}

Следовательно, для единичной сферы телесный угол сферической крышка задается как:

Ω = 4 π sin 2 ⁡ (θ 2) = 2 π (1 - cos ⁡ θ) {\ displaystyle \ Omega = 4 \ pi \ sin ^ {2} \ left ({\ frac {\ theta} {2}} \ right) = 2 \ pi \ left (1- \ cos {\ theta} \ right) \}

{\ displaystyle \ Omega = 4 \ pi \ sin ^ {2} \ left ({\ frac {\ theta} {2}} \ right) = 2 \ pi \ left (1- \ соз {\ тета} \ право) \}

Когда θ = π / 2, сферическая крышка становится полусферой с телесным углом 2π.

Телесный угол дополнения к конусу равен:

4 π - Ω = 2 π (1 + cos ⁡ θ) = 4 π cos 2 ⁡ (θ 2) {\ displaystyle 4 \ pi - \ Omega = 2 \ pi \ left (1+ \ cos {\ theta} \ right) = 4 \ pi \ cos ^ {2} \ left ({\ frac {\ theta} {2}} \ right)}

{\ displaystyle 4 \ pi - \ Omega = 2 \ pi \ left (1+ \ cos {\ theta} \ right) = 4 \ pi \ cos ^ {2} \ left ( {\ гидроразрыва {\ theta} {2}} \ right)}

Это также телесный угол той части небесной сферы, которую астрономический наблюдатель, находящийся на широте θ, может видеть при вращении Земли. На экваторе видна вся небесная сфера; на любом полюсе только одна половина.

Телесный угол, образованный сегментом сферической крышки, разрезанной плоскостью под углом γ от оси конуса и проходящей через вершину конуса, можно рассчитать по формуле:

Ω = 2 [arccos ⁡ (грех ⁡ γ грех ⁡ θ) - соз ⁡ θ arccos ⁡ (загар ⁡ γ загар ⁡ θ)] {\ displaystyle \ Omega = 2 \ left [\ arccos \ left ({\ frac {\ sin \ gamma} {\ sin \ theta}} \ right) - \ cos \ theta \ arccos \ left ({\ frac {\ tan \ gamma} {\ tan \ theta}} \ right) \ right] \}

\ Omega = 2 \ left [\ arccos \ left ({\ frac {\ sin \ gamma} {\ sin \ theta}} \ right) - \ cos \ theta \ arccos \ left ({\ frac {\ tan \ гамма} {\ tan \ theta}} \ right) \ right] \

Например, если γ = -θ, тогда формула сводится к формуле сферической крышки, приведенной выше: первый член становится π, а второй πcosθ.

Тетраэдр

Пусть OABC - это вершины тетраэдра с началом в точке O, к которому присоединяется треугольная грань ABC, где $a →, b →, c → {\ displaystyle {\ vec {a}} \, \, {\ vec {b}} \, \, {\ vec {c}}}$ ${\ vec {a}} \, \, {\ vec {b}} \, \, {\ vec {c}}$ - векторные позиции вершин A, B и C. Определите угол при вершине θ a как угол BOC и определите θ b, θ c соответственно. Пусть $ϕ ab {\ displaystyle \ phi _ {ab}}$ ${\ displaystyle \ phi _ {ab}}$ будет двугранным углом между плоскостями, содержащими тетраэдрические грани OAC и OBC, и определим $ϕ ac {\ displaystyle \ phi _ {ac}}$ ${\ displaystyle \ phi _ {ac }}$ , $ϕ bc {\ displaystyle \ phi _ {bc}}$ ${\ displaystyle \ phi _ {bc}}$ соответственно. Телесный угол Ω, образуемый треугольной поверхностью ABC, задается формулой

Ω = (ϕ ab + ϕ bc + ϕ ac) - π {\ displaystyle \ Omega = \ left (\ phi _ {ab} + \ phi _ { bc} + \ phi _ {ac} \ right) \ - \ pi \}

\ Omega = \ left (\ phi _ {ab} + \ phi _ {bc} + \ phi _ {ac} \ right) \ - \ pi \

Это следует из теории сферического избытка и приводит к тому, что существует аналогичная теорема теореме что «Сумма внутренних углов плоского треугольника равна π» для суммы четырех внутренних телесных углов тетраэдра следующим образом:

∑ i = 1 4 Ω i = 2 ∑ i = 1 6 ϕ я - 4 π {\ displaystyle \ sum _ {i = 1} ^ {4} \ Omega _ {i} = 2 \ sum _ {i = 1} ^ {6} \ phi _ {i} \ -4 \ pi \}

\ sum _ {i = 1} ^ {4} \ Omega _ {i} = 2 \ sum _ {i = 1} ^ {6} \ phi _ {i} \ - 4 \ pi \

где $ϕ i {\ displaystyle \ phi _ {i}}$ $\ phi _ {i}$ располагается по всем шести двугранным углам между любыми двумя плоскостями, которые содержат тетраэдрические грани OAB, OAC, OBC и ABC.

Полезная формула для вычисления телесного угла Ω, образованного треугольной поверхностью ABC, где $a →, b →, c → {\ displaystyle {\ vec {a}} \, \, { \ vec {b}} \, \, {\ vec {c}}}$ ${\ vec {a}} \, \, {\ vec {b}} \, \, {\ vec {c}}$ - векторные позиции ve точки A, B и C были даны Остеромом и Стракки (хотя результат был известен ранее Эйлером и Лагранжем):

tan ⁡ (1 2 Ω) = | a → b → c → | abc + (a → ⋅ b →) c + (a → ⋅ c →) b + (b → ⋅ c →) a {\ displaystyle \ tan \ left ({\ frac {1} {2}} \ Omega \ right) = {\ frac {\ left | {\ vec {a}} \ {\ vec {b}} \ {\ vec {c}} \ right |} {abc + \ left ({\ vec {a}} \ cdot {\ vec {b}} \ right) c + \ left ({\ vec {a}} \ cdot {\ vec {c}} \ right) b + \ left ({\ vec {b}} \ cdot {\ vec { c}} \ right) a}}}

\ tan \ left ({\ frac {1} {2}} \ Omega \ right) = {\ frac {\ left | {\ vec {a}} \ {\ vec {b }} \ {\ vec {c}} \ right |} {abc + \ left ({\ vec {a}} \ cdot {\ vec {b}} \ right) c + \ left ({\ vec {a}} \ cdot {\ vec {c}} \ right) b + \ left ({\ vec {b}} \ cdot {\ vec {c}} \ right) a}}

где

| a → b → c → | знак равно a → ⋅ (b → × c →) {\ displaystyle \ left | {\ vec {a}} \ {\ vec {b}} \ {\ vec {c}} \ right | = {\ vec {a} } \ cdot ({\ vec {b}} \ times {\ vec {c}})}

\ left | {\ vec {a}} \ {\ vec {b}} \ {\ vec {c}} \ right | = {\ vec {a}} \ cdot ({\ vec {b}} \ times {\ vec {c}})

обозначает тройное скалярное произведение трех векторов;

a → {\ displaystyle {\ vec {a}}}

{\ vec {a}}

- векторное представление точки A, а a - величина этого вектора (расстояние от начала до точки)

a → ⋅ b → {\ displaystyle {\ vec {a}} \ cdot {\ vec {b}}}

{\ vec {a}} \ cdot {\ vec {b}}

обозначает скалярное произведение.

. При реализации приведенного выше уравнения необходимо соблюдать осторожность функция, позволяющая избежать отрицательных или неправильных телесных углов. Одним из источников потенциальных ошибок является то, что скалярное тройное произведение может быть отрицательным, если a, b, c имеют неправильную обмотку . Вычисления - достаточное решение, поскольку никакая другая часть уравнения не зависит от обмотки. Другая ошибка возникает, когда скалярное тройное произведение положительно, а делитель отрицателен. В этом случае возвращается отрицательное значение, которое необходимо увеличить на π.

Еще одна полезная формула для вычисления телесного угла тетраэдра в начале координат O, который является чисто функцией углов при вершинах θ a, θ b, θ c определяется теоремой Л'Юилье как

tan ⁡ (1 4 Ω) = tan ⁡ (θ s 2) tan ⁡ (θ s - θ a 2) загар ⁡ (θ s - θ б 2) загар ⁡ (θ s - θ с 2) {\ displaystyle \ tan \ left ({\ frac {1} {4}} \ Omega \ right) = {\ sqrt {\ tan \ left ({\ frac {\ theta _ {s}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {a}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {b}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {c}} {2}} \ right)}}}

\ tan \ left ({\ frac {1} {4}} \ Omega \ right) = {\ sqrt {\ tan \ left ({\ frac {\ theta _ {s}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {a}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {b}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {c}} {2}} \ справа)}}

где

θ s = θ a + θ b + θ c 2 {\ displaystyle \ theta _ {s} = {\ frac {\ theta _ {a} + \ theta _ {b} + \ theta _ {c}} {2}}}

\ theta _ {s} = {\ frac {\ theta _ {a} + \ theta _ {b} + \ theta _ {c}} {2}}

Пирамида

Телесный угол четырехгранной правой прямоугольной пирамиды с вершиной углами a и b (двугранными углами, измеренными к противоположным боковым граням пирамиды) составляет

Ω = 4 arcsin ⁡ (sin ⁡ (a 2) sin ⁡ ( б 2)) {\ Displaystyle \ Omega = 4 \ arcsin \ left (\ sin \ left ({a \ over 2} \ right) \ sin \ left ({b \ over 2} \ right) \ right)}

\ Omega = 4 \ arc sin \ left (\ sin \ left ({a \ over 2} \ right) \ sin \ left ({b \ over 2} \ right) \ right)

Если обе стороны (α и β) основания пирамиды и расстояние (d) от центра базового прямоугольника до вершины пирамиды (центра сферы), то указанное выше уравнение можно изменить, чтобы получить

Ω Знак равно 4 arctan ⁡ α β 2 d 4 d 2 + α 2 + β 2 {\ displaystyle \ Omega = 4 \ arctan {\ frac {\ alpha \ beta} {2d {\ sqrt {4d ^ {2} + \ alpha ^ {2} + \ beta ^ {2}}}}}}

\ Omega = 4 \ arctan {\ гидроразрыва {\ альфа \ бета} {2d {\ sqrt {4d ^ {2} + \ alpha ^ {2} + \ beta ^ {2}}}}

Телесный угол прямой n-угольной пирамиды, в которой основание пирамиды представляет собой правильный n-сторонний многоугольник с описанным радиусом r, с высотой пирамиды h

Ω знак равно 2 π - 2 n arctan ⁡ (tan ⁡ (π n) 1 + r 2 h 2) {\ displaystyle \ Omega = 2 \ pi -2n \ arctan \ left ({\ frac {\ tan \ left ({\ pi \ over n} \ right)} {\ sqrt {1+ {r ^ {2} \ over h ^ {2}}}} \ right)}

\ Омега = 2 \ pi -2n \ arctan \ left ({\ frac {\ tan \ left ({\ pi \ over n} \ right)} {\ sqrt {1+ {r ^ {2} \ over h ^ {2 }}}}} \ right)

Телесный угол произвольной пирамиды с n-сторонняя база, определяемая последовательностью единичных векторов, представляющих ребра {s 1, s 2 },... s n, может быть эффективно вычислена по:

Ω = 2 π - arg ⁡ ∏ j = 1 n ((sj - 1 sj) (sjsj + 1) - (sj - 1 sj + 1) + i [sj - 1 sjsj + 1]) { \ Displaystyle \ Omega = 2 \ pi - \ arg \ prod _ {j = 1} ^ {n} \ left (\ left (s_ {j-1} s_ {j} \ right) \ left (s_ {j} s_ {j + 1} \ right) - \ left (s_ {j-1} s_ {j + 1} \ right) + i \ left [s_ {j-1} s_ {j} s_ {j + 1} \ right ] \ right)}

\ Omega = 2 \ pi - \ arg \ prod _ {j = 1 } ^ {n} \ left (\ left (s_ {j-1} s_ {j} \ right) \ left (s_ {j} s_ {j + 1} \ right) - \ left (s_ {j-1} s_ {j + 1} \ right) + i \ left [s_ {j-1} s_ {j} s_ {j + 1} \ right] \ right)

где круглые скобки (* *) - это скалярное произведение, а квадратные скобки [* * *] - это тройное скалярное произведение, а i - мнимая единица. Индексы циклически меняются: s 0 = s n и s 1 = s n + 1.

прямоугольник широты-долготы

Телесный угол прямоугольника широты и долготы на глобусе равен

(sin ⁡ ϕ N - sin ⁡ ϕ S) (θ E - θ W) sr {\ displaystyle \ left (\ sin \ phi _ {\ mathrm {N}} - \ sin \ phi _ {\ mathrm {S}} \ right) \ left (\ theta _ {\ mathrm {E}} - \ theta _ {\ mathrm {W}} \, \! \ right) \; \ mathrm {sr}}

{\ displaystyle \ left (\ sin \ phi _ {\ mathrm {N}} - \ si n \ phi _ {\ mathrm {S}} \ right) \ left (\ theta _ {\ mathrm {E}} - \ theta _ {\ mathrm {W}} \, \! \ right) \; \ mathrm { sr}}

где φ N и φ S - северная и южная линии широты ( измеряется от экватора в радианах с углом, увеличивающимся к северу), а θ E и θ W являются линиями востока и запада долгота (где угол в радианах увеличивается в восточном направлении). Математически это представляет собой дугу угла ϕ N - ϕ S, охватывающую сферу на θ E - θ W радиан. Когда долгота составляет 2π радиан, а широта - π радиан, телесный угол равен углу сферы.

Прямоугольник широты и долготы не следует путать с телесным углом прямоугольной пирамиды. Все четыре стороны прямоугольной пирамиды пересекают поверхность сферы по дугам большого круга. В прямоугольнике широты и долготы только линии долготы являются дугами большого круга; линий широты нет.

Солнце и Луна

Солнце видно с Земли при среднем угловом диаметре 0,5334 градуса или 9,310 × 10 радиан. Луна видна с Земли со средним угловым диаметром 9,22 × 10 радиан. Мы можем подставить их в приведенное выше уравнение для телесного угла, образованного конусом с вершиной углом 2θ:

Ω = 2 π (1 - cos ⁡ θ) {\ displaystyle \ Omega = 2 \ pi \ left (1- \ cos {\ theta} \ right)}

{\ displaystyle \ Omega = 2 \ пи \ влево (1- \ соз {\ тета} \ вправо)}

Результирующее значение для Солнца составляет 6,807 × 10 стерадиан. Результирующее значение для Луны составляет 6,67 × 10 стерадиан. Что касается всей небесной сферы, то Солнце и Луна увеличивают доли площади 0,000542% (5,42 ppm ) и 0,000531% (5,31 ppm) соответственно.. В среднем Солнце больше на небе, чем Луна, хотя оно намного, намного дальше.

Телесные углы в произвольных размерах

Телесный угол, образованный полной (d - 1) -мерной сферической поверхностью единичной сферы в d-мерном евклидовом пространстве, может быть определенным в любом количестве измерений d. Этот коэффициент телесного угла часто требуется при расчетах со сферической симметрией. Он задается формулой

Ω d = 2 π d 2 Γ (d 2) {\ displaystyle \ Omega _ {d} = {\ frac {2 \ pi ^ {\ frac {d} {2}}} {\ Gamma \ left ({\ frac {d} {2}} \ right)}} \}

\ Omega _ {d} = {\ frac {2 \ pi ^ {\ frac {d} {2}}} {\ Gamma \ left ({\ frac {d} {2}} \ right)}} \

где Γ - гамма-функция. Когда d является целым числом, гамма-функцию можно вычислить явно. Отсюда следует, что

Ω d = {1 (d 2 - 1)! 2 π d 2 d даже (1 2 (d - 1))! (d - 1)! 2 d π 1 2 (d - 1) d нечетное {\ displaystyle \ Omega _ {d} = {\ begin {cases} {\ frac {1} {\ left ({\ frac {d} {2}} - 1 \ right)!}} 2 \ pi ^ {\ frac {d} {2}} \ d {\ text {even}} \\ {\ frac {\ left ({\ frac {1} {2}} \ left (d-1 \ right) \ right)!} {(d-1)!}} 2 ^ {d} \ pi ^ {{\ frac {1} {2}} (d-1)} \ d {\ text {odd}} \ end {ases}}}

\ Omega _ { d} = {\ begin {cases} {\ frac {1} {\ left ({\ frac {d} {2}} - 1 \ right)!}} 2 \ pi ^ {\ frac {d} {2} } \ d {\ text {even}} \\ {\ frac {\ left ({\ frac {1} {2}} \ left (d-1 \ right) \ right)!} {(d-1)! }} 2 ^ {d} \ pi ^ {{\ frac {1} {2}} (d-1)} \ d {\ text {odd}} \ end {cases}}

Это дает ожидаемые результаты 4π стерадианов для трехмерной сферы, ограниченной поверхностью площадью 4πr и 2π радиан для двумерной окружности, ограниченной окружностью длиной 2πr. Это также дает немного менее очевидное значение 2 для одномерного случая, в котором одномерная «сфера» с центром в начале координат является интервалом [−r, r] и ограничена двумя предельными точками.

Аналог векторной формулы в произвольной размерности был получен Аомото и независимо Рибандо. Он выражает их как бесконечный многомерный ряд Тейлора:

Ω = Ω d | det ⁡ (V) | (4 π) d / 2 ∑ a → ∈ N (d 2) [(- 2) ∑ i < j a i j ∏ i < j a i j ! ∏ i Γ ( 1 + ∑ m ≠ i a i m 2) ] α → a →. {\displaystyle \Omega =\Omega _{d}{\frac {|\operatorname {det} (V)|}{(4\pi)^{d/2}}}\sum _{{\vec {a}}\in \mathbb {N} ^{\binom {d}{2}}}\left[{\frac {(-2)^{\sum _{i

{\ displaystyle \ Omega = \ Omega _ {d} {\ frac {| \ operatorname {det} (V) |} {(4 \ pi) ^ {d / 2}}} \ sum _ {{\ vec {a}} \ in \ mathbb {N} ^ {\ binom {d} {2}}} \ left [{\ frac {(-2) ^ {\ sum _ {i <j} a_ {ij}}} {\ prod _ {i <j} a_ {ij}!}} \ prod _ {i} \ Gamma \ left ({\ frac {1+ \ sum _ {m \ neq i} a_ {im}} {2}} \ right) \ right] {\ vec {\ alpha}} ^ {\ vec {a}}.}

Даны d единичных векторов $vi → {\ displaystyle {\ vec {v_ {i}}}}$ ${\ displaystyle {\ vec {v_ {i}}}}$ , определяя угол, пусть V обозначает матрицу, образованную их объединением, поэтому i-й столбец имеет вид $vi → {\ displaystyle {\ vec {v_ {i}}}}$ ${\ displaystyle {\ vec {v_ {i}}}}$ , и $α ij = vi → ⋅ vj → = α ji, α ii = 1 {\ displaystyle \ alpha _ {ij} = {\ vec {v_ {i}}} \ cdot {\ vec {v_ {j}} } = \ alpha _ {ji}, \ alpha _ {ii} = 1}$ ${\ displaystyle \ alpha _ {ij} = {\ vec {v_ {i}}} \ cdot {\ vec { v_ {j}}} = \ alpha _ {ji}, \ alpha _ {ii} = 1}$ . Переменные $α ij, 1 ≤ i < j ≤ d {\displaystyle \alpha _{ij},1\leq i$ ${\ displaystyle \ alpha _ {ij}, 1 \ leq i <j \ leq d}$ образуют многомерную $α → = (α 12,…, α 1 d, α 23,…, α d - 1, d) ∈ R (d 2) {\ displaystyle {\ vec {\ alpha}} = (\ alpha _ {12}, \ dotsc, \ alpha _ {1d}, \ alpha _ {23}, \ dotsc, \ alpha _ {d- 1, d}) \ in \ mathbb {R} ^ {\ binom {d} {2}}}$ ${\ displaystyle {\ vec {\ alpha}} = (\ alpha _ {12}, \ dotsc, \ alpha _ {1d}, \ alpha _ {23}, \ dotsc, \ alpha _ {d-1, d}) \ in \ mathbb {R} ^ {\ binom {d} {2}}}$ . Для «конгруэнтной» целочисленной мультиэкспоненты $a → = (a 12,…, a 1 d, a 23,…, ad - 1, d) ∈ N (d 2) {\ displaystyle {\ vec {a}} = (a_ {12}, \ dotsc, a_ {1d}, a_ {23}, \ dotsc, a_ {d-1, d}) \ in \ mathbb {N} ^ {\ binom {d} {2}} }$ ${\ displaystyle {\ vec {a}} = (a_ {12}, \ dotsc, a_ {1d}, a_ {23}, \ dotsc, a_ {d-1, d}) \ in \ mathbb {N} ^ {\ binom {d} {2}}}$ мы определяем $α → a → = ∏ α ijaij {\ displaystyle {\ vec {\ alpha}} ^ {\ vec {a}} = \ prod \ alpha _ {ij} ^ { а_ {ij}}}$ ${\ displaystyle {\ vec {\ альфа}} ^ {\ vec {a}} = \ prod \ alpha _ {ij} ^ {a_ {ij}}}$ . Обозначение $α ji {\ displaystyle \ alpha _ {ji}}$ ${\ displaystyle \ alpha _ {ji}}$ для $j>i {\ displaystyle j>i}$ $j>i$ означает переменную $α ij {\ displaystyle \ alpha _ {ij}}$ $\ alpha_ {ij}$ , аналогично для показателей $aji {\ displaystyle a_ {ji}}$ $a_ {ji}$ . Следовательно, термин $∑ m ≠ lalm {\ displaystyle \ sum _ {m \ neq l} a_ {lm}}$ ${\ displaystyle \ sum _ {m \ neq l} a_ {lm}}$ означает сумму по всем членам в $a → {\ displaystyle {\ vec {a}}}$ ${\ vec {a}}$ , где l отображается как первый или второй индекс. Когда этот ряд сходится, он сходится к телесному углу, определяемому векторами.

Ссылки

Дополнительная литература

Jaffey, AH (1954). «Телесный угол, образуемый круглой апертурой в точечных и рассеянных источниках: формулы и некоторые таблицы». Rev. Sci. Instrum. 25 . Pp. 349–354. Bibcode : 1954RScI... 25..349J. doi : 10.1063 / 1.17710 61.
Маскет, А. Виктор (1957). «Контурные интегралы телесного угла, ряды и таблицы». Rev. Sci. Instrum. 28 (3). п. 191. Bibcode : 1957RScI... 28..191M. doi : 10.1063 / 1.1746479.
Найто, Минору (1957). «Метод вычисления телесного угла, образуемого круглой апертурой». J. Phys. Soc. Jpn. 12 (10). С. 1122–1129. Bibcode : 1957JPSJ... 12.1122N. doi : 10.1143 / JPSJ.12.1122.
Пакстон, Ф. (1959). «Расчет телесного угла круглого диска». Rev. Sci. Instrum. 30 (4). п. 254. Bibcode : 1959RScI... 30..254P. doi : 10,1063 / 1,1716590.
Gardner, R.P.; Карнесейл, А. (1969). «Телесный угол, ограниченный в точке круглым диском». Nucl. Instrum. Методы. 73 (2). С. 228–230. Bibcode : 1969NucIM..73..228G. doi : 10.1016 / 0029-554X (69) 90214-6.
Gardner, R.P.; Verghese, К. (1971). «О телесном угле, образованном круговым диском». Nucl. Instrum. Методы. 93 (1). С. 163–167. Bibcode : 1971NucIM..93..163G. doi : 10.1016 / 0029-554X (71) 90155-8.
Асвестас, Джон С. Инглунд, Дэвид С. (1994). «Вычисление телесного угла, представленного плоской фигурой». Опт. Англ. 33 (12). С. 4055–4059. Bibcode : 1994OptEn..33.4055A. doi : 10.1117 / 12.183402.
Трика, Станислав (1997). «Угловое распределение телесного угла в точке, охватываемой круговым диском». Опт. Commun. 137 (4–6). С. 317–333. Bibcode : 1997OptCo.137..317T. doi : 10.1016 / S0030-4018 (96) 00789-4.
Прата, М. Дж. (2004). «Аналитический расчет телесного угла, полученного дисковым детектором с точечным косинусом». Nucl. Instrum. Методы Phys. Res. А. 521 . п. 576. arXiv : math-ph / 0305034. Bibcode : 2004NIMPA.521..576P. doi : 10.1016 / j.nima.2003.10.098.
Тимус, Д. М.; Prata, M. J.; Kalla, S.L.; Abbas, M. I.; Oner, F.; Галиано, Э. (2007). «Некоторые дальнейшие аналитические результаты о телесном угле, образованном в точке круглым диском с использованием эллиптических интегралов». Nucl. Instrum. Методы Phys. Res. А. 580 . С. 149–152. Bibcode : 2007NIMPA.580..149T. doi : 10.1016 / j.nima.2007.05.055.

На Викискладе есть материалы, связанные с Телесным углом.

Внешние ссылки

Теория многоугольника HCR ( телесный угол, образуемый любым многоугольником) из Academia.edu
Arthur P. Norton, A Star Atlas, Gall and Inglis, Edinburgh, 1969.
M. Г. Кендалл, Курс геометрии N измерений, № 8 Статистических монографий и курсов Гриффина, изд. М. Г. Кендалл, Чарльз Гриффин и Ко. Лтд., Лондон, 1961
Вайсштейн, Эрик У. "Solid Angle". MathWorld.