Тороидальные координаты

Иллюстрация тороидальных координат, которые получаются вращением двухмерной биполярной системы координат вокруг разделяющей оси его два фокуса. Фокусы расположены на расстоянии 1 от вертикальной оси z. Часть красной сферы, которая лежит над плоскостью $ xy $, является изоповерхностью σ = 30 °, синий тор - изоповерхностью τ = 0,5, а желтая полуплоскость - изоповерхностью φ = 60 °. Зеленая полуплоскость отмечает плоскость x-z, от которой отсчитывается φ. Черная точка расположена на пересечении красной, синей и желтой изоповерхностей с декартовыми координатами примерно (0,996, -1,725, 1,911).

Тороидальные координаты представляют собой трехмерные ортогональные система координат, которая возникает в результате вращения двухмерной биполярной системы координат вокруг оси, разделяющей два ее фокуса. Таким образом, два foci $F\; 1\; \{\backslash \; displaystyle\; F\_\; \{1\}\}$и $F\; 2\; \{\backslash \; displaystyle\; F\_\; \{2\}\}$в биполярных координатах стать кольцом радиуса $a\; \{\backslash \; displaystyle\; a\}$в $xy\; \{\backslash \; displaystyle\; xy\}$плоскости тороидального система координат; ось $z\; \{\backslash \; displaystyle\; z\}$- это ось вращения. Фокальное кольцо также известно как контрольный круг.

• 1 Определение
  • 1.1 Координатные поверхности
  • 1.2 Обратное преобразование
  • 1.3 Масштабные коэффициенты
• 2 Тороидальные гармоники
  • 2.1 Стандартное разделение
  • 2.2 Альтернативное разделение
• 3 Ссылки
• 4 Библиография
• 5 Внешние ссылки

Наиболее распространенное определение тороидальных координат $(\sigma ,\; \tau ,\; \varphi )\; \{\backslash \; displaystyle\; (\backslash \; sigma,\; \backslash \; tau,\; \backslash \; phi)\}$is

$x\; =\; a\; sinh\; \; \tau \; cosh\; \; \tau \; -\; cos\; \; \sigma \; cos\; \; \varphi \; \{\backslash \; displaystyle\; x\; =\; a\; \backslash \; \{\backslash \; frac\; \{\backslash \; sinh\; \backslash \; tau\}\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; соз\; \backslash \; сигма\}\}\; \backslash \; соз\; \backslash \; фи\}$

$у\; =\; а\; зп\; \; \tau \; сш\; \; т\; -\; соз\; \; \sigma \; грех\; \; \varphi \; \{\backslash \; Displaystyle\; у\; =\; а\; \backslash \; \{\backslash \; гидроразрыва\; \{\backslash \; зп\; \backslash \; тау\}\; \{\backslash \; соз\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\; \backslash \; sin\; \backslash \; phi\}$

$z\; =\; a\; sin\; cos\; \sigma \; cosh\; \; \tau \; -\; cos\; \; \sigma \; \{\backslash \; displaystyle\; z\; =\; a\; \backslash \; \{\backslash \; frac\; \{\backslash \; sin\; \backslash \; sigma\}\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\}$

вместе с $sign\; (\sigma )\; =\; sign\; (z\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{sign\}\; (\backslash \; sigma)\; =\; \backslash \; mathrm\; \{sign\}\; (z\}$). $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$координата точки $P\; \{\backslash \; displaystyle\; P\}$равна gle $F\; 1\; PF\; 2\; \{\backslash \; displaystyle\; F\_\; \{1\}\; PF\_\; \{2\}\}$и координата $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$равна натуральный логарифм отношения расстояний $d\; 1\; \{\backslash \; displaystyle\; d\_\; \{1\}\}$и $d\; 2\; \{\backslash \; displaystyle\; d\_\; \{2\}\}$к противоположным сторонам фокального кольца

$\tau \; =\; ln\; \; d\; 1\; d\; 2.\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \backslash \; ln\; \{\backslash \; frac\; \{d\_\; \{1\}\}\; \{d\_\; \{2\}\}\}.\}$

Диапазоны координат: и $\tau \; \ge \; 0\; \{\backslash \; displaystyle\; \backslash \; tau\; \backslash \; geq\; 0\}$и

Координатные поверхности

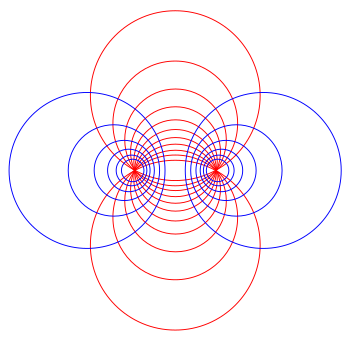
Вращение этой двумерной биполярной системы координат вокруг вертикальной оси дает трехмерная тороидальная система координат выше. Круг на вертикальной оси становится красной сферой, тогда как круг на горизонтальной оси становится синим тором.

Поверхности константы $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$соответствуют сферам разного радиуса

$(x\; 2\; +\; y\; 2)\; +\; (z\; -\; раскладушка\; \; \sigma )\; 2\; =\; a\; 2\; sin\; 2\; \; \sigma \; \{\backslash \; displaystyle\; \backslash \; left\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; \backslash \; right)\; +\; \backslash \; left\; (za\; \backslash \; cot\; \backslash \; sigma\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{\backslash \; sin\; ^\; \{2\}\; \backslash \; sigma\}\}\}$

что все проходят через фокальное кольцо, но не концентрически. Поверхности константы $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$представляют собой непересекающиеся торы разных радиусов

$z\; 2\; +\; (x\; 2\; +\; y\; 2\; -\; a\; coth\; \; \tau )\; 2\; =\; a\; 2\; зп\; 2\; \; \tau \; \{\backslash \; displaystyle\; z\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\}\; -\; a\; \backslash \; coth\; \backslash \; tau\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{\backslash \; sinh\; ^\; \{2\}\; \backslash \; tau\}\}\}$

, которые окружают фокальное кольцо. Центры сфер с константой- $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$лежат вдоль оси $z\; \{\backslash \; displaystyle\; z\}$, тогда как постоянная- $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$торы центрируются в плоскости $xy\; \{\backslash \; displaystyle\; xy\}$.

Обратное преобразование

Координаты $(\sigma ,\; \tau ,\; \varphi )\; \{\backslash \; displaystyle\; (\backslash \; sigma,\; \backslash \; tau,\; \backslash \; phi)\}$могут быть вычислены из Декартовы координаты (x, y, z) выглядят следующим образом. Азимутальный угол $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$дается формулой

$tan\; \; \varphi \; =\; yx\; \{\backslash \; displaystyle\; \backslash \; tan\; \backslash \; phi\; =\; \{\backslash \; frac\; \{y\}\; \{x\}\}\; \}$

Цилиндрический радиус $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$точки P определяется как

$\rho \; 2\; =\; x\; 2\; +\; y\; 2\; \{\backslash \; displaystyle\; \backslash \; rho\; ^\; \{2\}\; =\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}$

, а расстояние от него до фокусов в плоскости, определенной как $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$, определяется как

$d\; 1\; 2\; знак\; равно\; (\rho \; +\; a)\; 2\; +\; z\; 2\; \{\backslash \; displaystyle\; d\_\; \{1\}\; ^\; \{2\}\; =\; (\backslash \; rho\; +\; a)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\}$

$d\; 2\; 2\; =\; (\rho \; -\; a)\; 2\; +\; z\; 2\; \{\backslash \; displaystyle\; d\_\; \{2\}\; ^\; \{2\}\; =\; (\backslash \; rho\; -a)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\}$

Геометрическая интерпретация координат σ и τ точки П . Наблюдаемые в плоскости постоянного азимутального угла $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$, тороидальные координаты эквивалентны биполярным координатам. Угол $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$образован двумя фокусами в этой плоскости и P, тогда как $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$- логарифм отношения расстояний до фокусов. Соответствующие круги константы $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$и $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$показаны красным и синим цветом соответственно и пересекаются в прямые углы (пурпурный прямоугольник); они ортогональны.

Координата $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$равна натуральному логарифму фокусных расстояний

$\tau \; =\; ln\; \; d\; 1\; d\; 2\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \backslash \; ln\; \{\backslash \; frac\; \{d\_\; \{1\}\}\; \{d\_\; \{2\}\}\}\}$

тогда как $|\; \sigma \; |\; \{\backslash \; displaystyle\; |\; \backslash \; sigma\; |\}$равен углу между лучами и фокусами, который можно определить по закону косинусов

$cos\; \; \sigma \; =\; d\; 1\; 2\; +\; d\; 2\; 2\; -\; 4\; а\; 2\; 2\; д\; 1\; д\; 2.\; \{\backslash \; displaystyle\; \backslash \; cos\; \backslash \; sigma\; =\; \{\backslash \; frac\; \{d\_\; \{1\}\; ^\; \{2\}\; +\; d\_\; \{2\}\; ^\; \{2\}\; -4a\; ^\; \{2\}\}\; \{2d\_\; \{1\}\; d\_\; \{2\}\}\}.\}$

Или явно, включая знак,

$\sigma \; =\; sign\; (z)\; arccos\; \; r\; 2\; -\; a\; 2\; ((r\; 2\; +\; a\; 2)\; 2-4\; \rho \; 2\; a\; 2\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \backslash \; mathrm\; \{sign\; \}\; (z)\; \backslash \; arccos\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; -a\; ^\; \{2\}\}\; \{\backslash \; sqrt\; \{((r\; ^\; \{2\}\; +\; a\; ^\; \{2\})\; ^\; \{2\}\; -4\; \backslash \; rho\; ^\; \{\; 2\}\; a\; ^\; \{2\}\}\}\}$

где $r\; =\; x\; 2\; +\; y\; 2\; +\; z\; 2\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\}\}\}$.

Преобразования между цилиндрическими и тороидальными координатами могут быть выражены в сложных обозначениях как

$z\; +\; i\; \rho \; =\; ia\; coth\; \; \tau \; +\; i\; \sigma \; 2,\; \{\backslash \; displaystyle\; z\; +\; i\; \backslash \; rho\; \backslash \; =\; ia\; \backslash \; coth\; \{\backslash \; frac\; \{\backslash \; tau\; +\; i\; \backslash \; sigma\}\; \{2\}\},\}$

$\tau \; +\; i\; \sigma \; =\; ln\; \; z\; +\; i\; (\rho \; +\; a)\; z\; -\; i\; (\rho \; -\; a).\; \{\backslash \; displaystyle\; \backslash \; tau\; +\; i\; \backslash \; sigma\; \backslash \; =\; \backslash \; ln\; \{\backslash \; frac\; \{z\; +\; i\; (\backslash \; rho\; +\; a)\}\; \{zi\; (\backslash \; rho\; -a)\}\}.\}$

Коэффициенты масштабирования

Масштаб коэффициенты для тороидальных координат $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$и $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$равны

$h\; \sigma \; =\; h\; \tau \; =\; a\; соз\; \; \tau \; -\; соз\; \; \sigma \; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; sigma\}\; =\; h\; \_\; \{\backslash \; tau\}\; =\; \{\backslash \; frac\; \{a\}\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; c\; os\; \backslash \; sigma\}\}\}$

тогда как коэффициент азимутального масштабирования равен

$h\; \varphi \; =\; a\; sinh\; \; \tau \; ch\; \; \tau \; -\; cos\; \; \sigma \; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; phi\}\; =\; \{\backslash \; frac\; \{a\; \backslash \; sinh\; \backslash \; tau\; \}\; \{\backslash \; ch\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\}$

Таким образом, бесконечно малый элемент объема равен

$d\; V\; =\; a\; 3\; sinh\; \; \tau \; (ch\; \; \tau \; -\; cos\; \; \sigma )\; 3\; d\; \sigma \; d\; \tau \; d\; \varphi \; \{\backslash \; displaystyle\; dV\; =\; \{\backslash \; frac\; \{a\; ^\; \{3\}\; \backslash \; sinh\; \backslash \; tau\}\; \{\backslash \; left\; (\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\; \backslash \; right)\; ^\; \{3\}\}\}\; \backslash ,\; d\; \backslash \; sigma\; \backslash ,\; d\; \backslash \; tau\; \backslash ,\; d\; \backslash \; phi\}$

, а лапласиан определяется как

$\nabla \; 2\; \Phi \; =\; (ch\; \; \tau \; -\; cos\; \; \sigma )\; 3\; a\; 2\; sinh\; \; \tau \; [sinh\; \; \tau \; \partial \; \partial \; \sigma \; (1\; ch\; \; \tau \; -\; cos\; \; \sigma \; \partial \; \Phi \; \partial \; \sigma )\; +\; \partial \; \partial \; \tau \; (sinh\; \; \tau \; ch\; \; \tau \; -\; cos\; \; \sigma \; \partial \; \Phi \; \partial \; \tau )\; +\; 1\; sinh\; \; \tau \; (cosh\; \; \tau \; -\; cos\; \; \sigma )\; \partial \; 2\; \Phi \; \partial \; \varphi \; 2\; ]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; Phi\; =\; \{\backslash \; frac\; \{\backslash \; left\; (\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\; \backslash \; right)\; ^\; \{3\}\}\; \{a\; ^\; \{2\}\; \backslash \; sinh\; \backslash \; tau\}\}\; \backslash \; left\; [\backslash \; sinh\; \backslash \; tau\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; sigma\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; sigma\}\}\; \backslash \; right)\; \backslash \; right.\; \backslash \backslash \; [8pt]\; \{\}\; \backslash \; quad\; +\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; tau\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; sinh\; \backslash \; tau\}\; \{\backslash \; ch\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; tau\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sinh\; \backslash \; tau\; \backslash \; left\; (\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\; \backslash \; right)\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; phi\; ^\; \{2\}\}\}\; \backslash \; right]\; \backslash \; end\; \{align\}\}\}$

Другие дифференциальные операторы, такие как $\nabla \; \cdot \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\}$и $\nabla \; \times \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\}$может быть выражено в координатах $(\sigma ,\; \tau ,\; \varphi )\; \{\backslash \; displaystyle\; (\backslash \; sigma,\; \backslash \; tau,\; \backslash \; phi)\}$путем замены масштабных коэффициентов в общие формулы, найденные в ортогональные координаты.

Стандартное разделение

Три переменных Уравнение Лапласа

$\nabla \; 2\; \Phi \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; Phi\; =\; 0\}$

допускает решение через разделение переменных в тороидальных координатах. Делая замену

$\Phi \; =\; U\; cosh\; \; \tau \; -\; cos\; \; \sigma \; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; U\; \{\backslash \; sqrt\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\}$

, получается разделимое уравнение. Частное решение, полученное с помощью разделения переменных, выглядит следующим образом:

$\Phi \; =\; cosh\; \; \tau \; -\; cos\; \; \sigma \; S\; \nu \; (\sigma )\; T\; \mu \; \nu \; (\tau )\; V\; \mu \; (\varphi )\; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; \{\backslash \; sqrt\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}\; \backslash ,\; \backslash ,\; S\; \_\; \{\backslash \; nu\}\; (\backslash \; sigma)\; T\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; (\backslash \; tau)\; V\; \_\; \{\backslash \; mu\}\; (\backslash \; phi)\}$

где каждая функция представляет собой линейную комбинацию:

$S\; \nu \; (\sigma )\; =\; ei\; \nu \; \sigma \; и\; -\; i\; \nu \; \sigma \; \{\backslash \; displaystyle\; S\; \_\; \{\backslash \; nu\}\; (\backslash \; sigma)\; =\; e\; ^\; \{i\; \backslash \; nu\; \backslash \; sigma\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathrm\; \{и\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; i\; \backslash \; nu\; \backslash \; sigma\}\}$

$T\; \mu \; \nu \; (\tau )\; =\; P\; \nu \; -\; 1/2\; \mu \; (\; соз\; \; \tau )\; и\; Q\; \nu \; -\; 1/2\; \mu \; (соз\; \tau )\; \{\backslash \; displaystyle\; T\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; (\backslash \; tau)\; =\; P\; \_\; \{\backslash \; nu\; -1/2\}\; ^\; \{\backslash \; mu\}\; (\backslash \; cosh\; \backslash \; tau)\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathrm\; \{and\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; Q\; \_\; \{\backslash \; nu\; -1/2\}\; ^\; \{\backslash \; mu\}\; (\backslash \; ch\; \backslash \; tau)\}$

$V\; \mu \; (\; \varphi )\; знак\; равно\; ei\; \mu \; \varphi \; и\; -\; я\; \mu \; \varphi \; \{\backslash \; Displaystyle\; V\; \_\; \{\backslash \; mu\}\; (\backslash \; phi)\; =\; e\; ^\; \{i\; \backslash \; mu\; \backslash \; phi\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathrm\; \{и\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; i\; \backslash \; mu\; \backslash \; phi\}\}$

Где P и Q - связанные функции Лежандра первого и второго рода. Эти функции Лежандра часто называют тороидальными гармониками.

Тороидальные гармоники обладают множеством интересных свойств. Если вы сделаете замену переменной $z\; =\; cosh\; \; \tau >1\; \{\backslash \; displaystyle\; z\; =\; \backslash \; cosh\; \backslash \; tau>1\}$затем, например, с порядком исчезновения $\mu \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mu\; =\; 0\}$(по соглашению не записывать порядок, когда он исчезает) и $\nu \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nu\; =\; 0\}$

$Q\; -\; 1\; 2\; (z)\; =\; 2\; 1\; +\; z\; K\; (\; 2\; 1\; +\; z)\; \{\backslash \; displaystyle\; Q\; \_\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (z)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{1\; +\; z\}\}\}\; K\; \backslash \; left\; (\{\backslash \; sqrt\; \{\; \backslash \; frac\; \{2\}\; \{1\; +\; z\}\}\}\; \backslash \; right)\}$

и

$P\; -\; 1\; 2\; (z)\; =\; 2\; \pi \; 2\; 1\; +\; z\; K\; (z\; -\; 1\; z\; +\; 1)\; \{\backslash \; displaystyle\; P\_\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (z)\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{1\; +\; z\}\}\}\; K\; \backslash \; left\; (\{\backslash \; sqrt\; \{\backslash \; frac\; \{z-1\}\; \{z\; +\; 1\}\}\}\; \backslash \; right)\}$

где $K\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; K\}$и $E\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; E\}$- это полные эллиптические интегралы типа первого и второго соответственно. Остальные тороидальные гармоники можно получить d, например, в терминах полных эллиптических интегралов, используя рекуррентные соотношения для ассоциированных функций Лежандра.

Классические применения тороидальных координат заключаются в решении уравнений в частных производных, например, уравнения Лапласа, для которого тороидальные координаты допускают разделение переменных или уравнение Гельмгольца, для которого тороидальные координаты не позволяют разделить переменные. Типичными примерами могут быть электрический потенциал и электрическое поле проводящего тора или, в вырожденном случае, кольцо электрического тока (Hulme 1982).

Альтернативное разделение

В качестве альтернативы можно сделать другую замену (Andrews 2006)

$\Phi \; =\; U\; \rho \; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; \{\backslash \; frac\; \{U\}\; \{\backslash \; sqrt\; \{\; \backslash \; rho\}\}\}\}$

где

$\rho \; =\; x\; 2\; +\; y\; 2\; =\; a\; sh\; \; \tau \; ch\; \; \tau \; -\; cos\; \; \sigma .\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{a\; \backslash \; sinh\; \backslash \; tau\}\; \{\backslash \; cosh\; \backslash \; tau\; -\; \backslash \; cos\; \backslash \; sigma\}\}.\}$

Снова получается разделимое уравнение. Частное решение, полученное с помощью разделения переменных, тогда:

$\Phi \; =\; a\; \rho \; S\; \nu \; (\sigma )\; T\; \mu \; \nu \; (\tau )\; V\; \mu \; (\varphi )\; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; \{\backslash \; frac\; \{\; a\}\; \{\backslash \; sqrt\; \{\backslash \; rho\}\}\}\; \backslash ,\; \backslash ,\; S\; \_\; \{\backslash \; nu\}\; (\backslash \; sigma)\; T\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; (\backslash \; tau)\; V\; \_\; \{\backslash \; mu\}\; (\backslash \; phi)\}$

где каждый функция представляет собой линейную комбинацию:

$S\; \nu \; (\sigma )\; =\; ei\; \nu \; \sigma \; и\; -\; я\; \nu \; \sigma \; \{\backslash \; displaystyle\; S\; \_\; \{\backslash \; nu\}\; (\backslash \; sigma)\; =\; e\; ^\; \{i\; \backslash \; nu\; \backslash \; sigma\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathrm\; \{и\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; i\; \backslash \; nu\; \backslash \; sigma\}\}$

$T\; \mu \; \nu \; (\tau )\; =\; P\; \mu \; -\; 1/2\; \nu \; (coth\; \; \tau )\; и\; Q\; \mu \; -\; 1/2\; \nu \; (coth\; \; \tau )\; \{\backslash \; Displaystyle\; T\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; (\backslash \; tau)\; =\; P\; \_\; \{\backslash \; mu\; -1/2\}\; ^\; \{\backslash \; nu\}\; (\backslash \; coth\; \backslash \; tau)\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathrm\; \{and\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; Q\; \_\; \{\backslash \; mu\; -1/2\}\; ^\; \{\backslash \; nu\}\; (\backslash \; coth\; \backslash \; tau)\}$

$V\; \mu \; (\varphi )\; =\; ei\; \mu \; \varphi \; и\; -\; i\; \mu \; \varphi .\; \{\backslash \; Displaystyle\; В\; \_\; \{\backslash \; му\}\; (\backslash \; фи)\; =\; е\; ^\; \{я\; \backslash \; му\; \backslash \; фи\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathrm\; \{и\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; е\; ^\; \{-\; я\; \backslash \; му\; \backslash \; phi\}.\}$

Обратите внимание, что, хотя тороидальные гармоники снова используются для функции T, аргумент $coth\; \; \tau \; \{\backslash \; displaystyle\; \backslash \; coth\; \backslash \; tau\}$, а не $cosh\; \; \tau \; \{\backslash \; displaystyle\; \backslash \; cosh\; \backslash \; tau\}$и $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$и $\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$обменены индексы. Этот метод полезен в ситуациях, в которых граничные условия не зависят от сферического угла $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, например заряженное кольцо, бесконечная полуплоскость или две параллельные плоскости. Для тождеств, связывающих тороидальные гармоники с гиперболическим косинусом аргумента с гармониками гиперболического котангенса аргумента, см. формулы Уиппла.

• Байерли, У., цилиндрические и эллипсоидальные гармоники с приложениями к задачам математической физики Ginn co. С. 264–266
• Arfken G (1970). Математические методы для физиков (2-е изд.). Орландо, Флорида: Academic Press. С. 112–115.
• Эндрюс, Марк (2006). «Альтернативное разделение уравнения Лапласа в тороидальных координатах и ​​его приложение к электростатике». Журнал электростатики. 64 (10): 664–672. CiteSeerX 10.1.1.205.5658. doi : 10.1016 / j.elstat.2005.11.005.
• Халм, А. (1982). «Заметка о магнитном скалярном потенциале электрического тока-кольца». Математические труды Кембриджского философского общества. 92 (1): 183–191. doi : 10.1017 / S0305004100059831.

• Морс П. М., Фешбах Н. (1953). Методы теоретической физики, часть I. Нью-Йорк: МакГроу – Хилл. п. 666.
• Корн Г. А., Корн Т. М. (1961). Математический справочник для ученых и инженеров. Нью-Йорк: Макгроу-Хилл. п. 182. LCCN 59014456.
• Маргенау Х., Мерфи Г.М. (1956). Математика физики и химии. Нью-Йорк: Д. ван Ностранд. Стр. 190 –192. LCCN 55010911.
• Мун П. Х., Спенсер Д. Э. (1988). «Тороидальные координаты (η, θ, ψ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (2-е изд., 3-е исправленное печатное издание). Нью-Йорк: Springer Verlag. С. 112–115 (Раздел IV, E4Ry). ISBN 978-0-387-02732-6.

• MathWorld описание тороидальных координат