Spin glass

редактировать

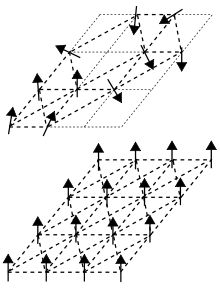
Схематическое изображение случайной спиновой структуры спинового стакана (вверху) и упорядоченный один из ферромагнетика (внизу)

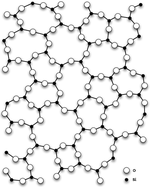
Стекло (аморфный SiO 2)

Кварц (кристаллический SiO 2)) Магнитный беспорядок спинового стекла по сравнению с ферромагнетиком аналогичен относительно позиционного беспорядка стекла (слева) по сравнению с кварцем (справа).

В физике конденсированного состояния спиновое стекло является моделью определенного типа Магнит. Магнитные спины, грубо говоря, представляют собой ориентацию северного и южного магнитных полюсов в трехмерном пространстве. В ферромагнитных твердых телах магнитные спины составляющих атомов атомов все выровнены Спиновые стекла контрастируют с ферромагнетиками как «неупорядоченные » магниты, в которых спины их атомов не выровнены по регулярной схеме.

Термин «стекло» происходит от аналогия между магнитным беспорядком в спине g Класс и беспорядок положения обычного химического стекла, например оконного стекла. В оконном стекле или любом аморфном твердом теле структура атомных связей сильно нерегулярна; напротив, кристалл имеет однородную структуру атомных связей. В ферромагнитных твердых телах все магнитные спины ориентированы в одном направлении; это аналог структуры кристалла на основе решетки.

Отдельные атомные связи в спиновом стекле представляют собой смесь примерно равного количества ферромагнитных связей (где соседи имеют одинаковую ориентацию) и антиферромагнитных связи (где соседи имеют прямо противоположную ориентацию: северный и южный полюса перевернуты на 180 градусов). Эти паттерны выровненных и несовпадающих атомных магнитов создают так называемые фрустрированные взаимодействия - искажения в геометрии атомных связей по сравнению с тем, что можно было бы увидеть в обычном, полностью выровненном твердом теле. Они также могут создавать ситуации, когда стабильно более чем одно геометрическое расположение атомов.

Спиновые стекла и сложные внутренние структуры, возникающие внутри них, называются «метастабильными », потому что они «застревают» в стабильных конфигурациях, отличных от конфигурации с наименьшей энергией (который был бы совмещенным и ферромагнитным). Математическую сложность этих структур трудно, но полезно изучить экспериментально или в моделированиях ; с приложениями к физике, химии, материаловедению и искусственным нейронным сетям в информатике.

Содержание

1 Магнитное поведение
2 Модель Эдвардса – Андерсона
3 Модель Шеррингтона и Киркпатрика
4 Модель с бесконечным диапазоном
5 Неэргодическое поведение и приложения
6 Самоиндуцированное спиновое стекло
7 История поля
8 См. Также
9 Примечания
10 Ссылки
11 Литература
12 Внешние ссылки

Магнитные свойства

Это временная зависимость отличает спиновые стекла от других магнитных систем.

Выше температуры перехода спинового стекла , T c спиновое стекло демонстрирует типичное магнитное поведение (такое как парамагнетизм ).

Если магнитное поле приложено, когда образец охлаждается до температуры перехода, намагниченность образца увеличивается, как описано законом Кюри. При достижении T c образец становится спиновым стеклом, и дальнейшее охлаждение приводит к небольшому изменению намагниченности. Это называется намагничиванием с полевым охлаждением.

Когда внешнее магнитное поле удаляется, намагниченность спинового стекла быстро падает до более низкого значения, известного как остаточная намагниченность.

Затем намагниченность медленно спадает по мере приближения к нулю (или некоторой небольшой части исходного значения - это остается неизвестным ). Это затухание не является экспоненциальным, и никакая простая функция не может адекватно соответствовать кривой намагниченности в зависимости от времени. Этот медленный распад характерен для спиновых стекол. Экспериментальные измерения в течение нескольких дней показали постоянные изменения, превышающие уровень шума оборудования.

Спиновые стекла отличаются от ферромагнетиков тем, что после удаления внешнего магнитного поля с ферромагнетика намагниченность остается неопределенной. по остаточной стоимости. Парамагнетики отличаются от спиновых стекол тем, что после снятия внешнего магнитного поля намагниченность быстро падает до нуля без остаточной намагниченности. Затухание быстрое и экспоненциальное.

Если образец охлаждают ниже T c в отсутствие внешнего магнитного поля и магнитное поле прикладывается после перехода в фазу спинового стекла, происходит быстрое начальное увеличение до значения, называемого намагниченностью при нулевом охлаждении поля. Затем происходит медленный дрейф вверх в сторону намагниченности, охлаждаемой полем.

Удивительно, но сумма двух сложных функций времени (охлаждение с нулевым полем и остаточная намагниченность) является постоянной величиной, а именно значением с полевым охлаждением, и, таким образом, обе имеют идентичные функциональные формы с течением времени, при хотя бы в пределе очень малых внешних полей.

Модель Эдвардса – Андерсона

В этой модели у нас есть спины, расположенные на $d {\ displaystyle d}$ $d$ -мерной решетке с подобными взаимодействиями только ближайших соседей. к модели Ising. Эта модель может быть решена точно для критических температур, и стеклообразная фаза наблюдается при низких температурах. Гамильтониан для этой спиновой системы задается следующим образом:

H = - ∑ ⟨ij⟩ J ij S i S j, {\ displaystyle H = - \ sum _ {\ langle ij \ rangle} J_ {ij} S_ {i} S_ {j},}

{\ displaystyle H = - \ sum _ {\ langle ij \ rangle} J_ {ij} S_ {i} S_ {j},}

где $S i {\ displaystyle S_ {i}}$ $S_ {i}$ относится к спиновой матрице Паули для Половина спина частицы в точке решетки $i {\ displaystyle i}$ $i$ . Отрицательное значение $J ij {\ displaystyle J_ {ij}}$ $J_ {ij}$ обозначает взаимодействие антиферромагнитного типа между спинами в точках $i {\ displaystyle i}$ $i$ и $j {\ displaystyle j}$ $j$ . Сумма проходит по всем ближайшим соседним позициям на решетке любой размерности. Переменные $J i j {\ displaystyle J_ {ij}}$ $J_ {ij}$ , представляющие магнитную природу спин-спиновых взаимодействий, называются связующими переменными.

Чтобы определить статистическую сумму для этой системы, необходимо усреднить свободную энергию $f [J ij] = - 1 β ln ⁡ Z [J ij] {\ displaystyle f \ left [ J_ {ij} \ right] = - {\ frac {1} {\ beta}} \ ln {\ mathcal {Z}} \ left [J_ {ij} \ right]}$ ${\ displaystyle f \ left [J_ {ij} \ right] = - {\ frac {1} {\ beta }} \ ln {\ mathcal {Z}} \ left [J_ {ij} \ right]}$ где $Z [J ij] = Tr S ⁡ (е - β H) {\ displaystyle {\ mathcal {Z}} \ left [J_ {ij} \ right] = \ operatorname {Tr} _ {S} \ left (e ^ {- \ beta H} \ right)}$ ${\ displaystyle {\ mathcal {Z}} \ left [J_ {ij } \ right] = \ OperatorName {Tr} _ {S} \ left (e ^ {- \ beta H} \ right)}$ по всем возможным значениям $J ij {\ displaystyle J_ {ij}}$ $J_ {ij}$ . Распределение значений $J ij {\ displaystyle J_ {ij}}$ $J_ {ij}$ считается гауссовым со средним значением $J 0 {\ displaystyle J_ {0}}$ $J_ {0}$ и дисперсия $J 2 {\ displaystyle J ^ {2}}$ $J ^ {2}$ :

P (J ij) = N 2 π J 2 exp ⁡ {- N 2 J 2 (J ij - J 0 N) 2 }. {\ Displaystyle P (J_ {ij}) = {\ sqrt {\ frac {N} {2 \ pi J ^ {2}}}} \ exp \ left \ {- {\ frac {N} {2J ^ {2 }}} \ left (J_ {ij} - {\ frac {J_ {0}} {N}} \ right) ^ {2} \ right \}.}

{\ displaystyle P (J_ {ij}) = {\ sqrt {\ frac {N} {2 \ pi J ^ {2}}}} \ exp \ left \ {- {\ frac {N} {2J ^ {2}}} \ left (J_ {ij} - {\ frac {J_ {0}} {N}} \ right) ^ {2} \ right \}.}

Решение для свободной энергии с использованием Метод реплики, ниже определенной температуры обнаруживается новая магнитная фаза, называемая фазой спинового стекла (или стеклообразной фазой) системы, которая характеризуется исчезающей намагниченностью $m = 0 {\ displaystyle m = 0}$ $m = 0$ вместе с ненулевым значением двухточечной корреляционной функции между спинами в одной и той же точке решетки, но в двух разных репликах:

q = ∑ i = 1 NS i α S i β ≠ 0, {\ displaystyle q = \ sum _ {i = 1} ^ {N} S_ {i} ^ {\ alpha} S_ {i} ^ {\ beta} \ neq 0,}

{\ displaystyle q = \ sum _ {i = 1} ^ {N} S_ {i} ^ {\ alpha} S_ {i} ^ {\ beta} \ neq 0,}

где $α, β {\ displaystyle \ alpha, \ beta}$ $\ alpha, \ beta$ - индексы реплик. параметр порядка для фазового перехода ферромагнетик в спиновое стекло, следовательно, равен $q {\ displaystyle q}$ $q$ , а для парамагнетика в спиновое стекло снова равен $q {\ displaystyle q}$ $q$ . Следовательно, новый набор параметров порядка, описывающих три магнитные фазы, состоит из $m {\ displaystyle m}$ $m$ и $q {\ displaystyle q}$ $q$ .

В предположении симметрии реплики, свободная энергия среднего поля определяется выражением:

β f = - β 2 J 2 4 (1 - q) 2 + β J 0 m 2 2 - ∫ exp ⁡ (- z 2 2) log ⁡ ( 2 ch ⁡ (β J z + β J 0 m)) dz. {\ displaystyle {\ begin {align} \ beta f = {} - {\ frac {\ beta ^ {2} J ^ {2}} {4}} (1-q) ^ {2} + {\ frac {\ beta J_ {0} m ^ {2}} {2}} \\ - \ int \ exp \ left (- {\ frac {z ^ {2}} {2}} \ right) \ log \ left (2 \ cosh \ left (\ beta Jz + \ beta J_ {0} m \ right) \ right) \, \ mathrm {d} z. \ End {align}}}

{\ displaystyle {\ begin {align} \ бета f = {} - {\ frac {\ beta ^ {2} J ^ {2}} {4}} (1-q) ^ {2} + {\ frac {\ beta J_ {0} m ^ { 2}} {2}} \\ - \ int \ exp \ left (- {\ frac {z ^ {2}} {2}} \ right) \ log \ left (2 \ ch \ left (\ beta Jz + \ beta J_ {0} m \ right) \ right) \, \ mathrm {d} z. \ end {align}}}

Модель Шеррингтона и Киркпатрика

Помимо необычных экспериментальных свойств спиновые стекла являются предметом обширных теоретических и вычислительных исследований. Значительная часть ранних теоретических работ по спиновым стеклам касалась формы теории среднего поля, основанной на наборе реплик статистической суммы системы.

Важная, точно решаемая модель спинового стекла была предложена Дэвидом Шеррингтоном и Скоттом Киркпатриком в 1975 году. Это модель Изинга с фрустрированными ферро-ферро-ферроотсеками на больших расстояниях. а также антиферромагнитные муфты. Это соответствует приближению среднего поля спиновых стекол, описывающему медленную динамику намагниченности и сложное неэргодическое состояние равновесия.

В отличие от модели Эдвардса – Андерсона (EA), хотя в системе рассматриваются только двухспиновые взаимодействия, диапазон каждого взаимодействия потенциально может быть бесконечным (порядка размера решетки). Таким образом, мы видим, что любые два спина могут быть связаны ферромагнитной или антиферромагнитной связью, и их распределение дается точно так же, как в случае модели Эдвардса – Андерсона. Гамильтониан для модели SK очень похож на модель EA:

H = - ∑ i < j J i j S i S j {\displaystyle H=-\sum _{i

H = - \ sum_ {i <j} J_ {ij} S_i S_j

, где $J ij, S i, S j {\ displaystyle J_ {ij}, S_ {i}, S_ {j}}$ ${\ displaystyle J_ {ij}, S_ {i}, S_ {j}}$ имеют те же значения, что и в модели EA. Равновесное решение модели после некоторых первоначальных попыток Шеррингтона, Киркпатрика и других было найдено Джорджио Паризи в 1979 году с помощью метода реплик. Последующая работа по интерпретации решения Паризи - М. Мезаром, Ж. Паризи, М. А. Вирасоро и многими другими - выявила сложную природу стекловидной низкотемпературной фазы, характеризующейся нарушением эргодичности, ультраметричностью и несамоусредненностью. Дальнейшие разработки привели к созданию метода полости, который позволил исследовать низкотемпературную фазу без реплик. Строгое доказательство решения Паризи было предоставлено в работе Франческо Герра и Мишеля Талаграна.

Формализм теории среднего поля реплики также применялся при изучении нейронной сетей, где он позволяет вычислять такие свойства, как емкость памяти простых архитектур нейронных сетей, не требуя разработки или реализации алгоритма обучения (такого как обратное распространение ).

Более реалистичные модели спинового стекла с короткодействующими фрустрированными взаимодействиями и беспорядком, такие как модель Гаусса, в которой связи между соседними спинами следуют распределению Гаусса, также широко изучались, особенно с использованием Моделирование Монте-Карло. Эти модели отображают фазы спинового стекла, граничащие с резкими фазовыми переходами.

Помимо своей значимости для физики конденсированных сред, теория спинового стекла приобрела строго междисциплинарный характер, с приложениями к теории нейронных сетей, информатике, теоретическая биология, эконофизика и др.

Модель с бесконечным радиусом действия

Модель с бесконечным радиусом действия является обобщением модели Шеррингтона – Киркпатрика, где мы рассматриваем не только два спиновых взаимодействия, но и $r { \ displaystyle r}$ $r$ -спиновые взаимодействия, где $r ≤ N {\ displaystyle r \ leq N}$ $r \ leq N$ и $N {\ displaystyle N}$ $N$ - общее количество вращений. В отличие от модели Эдвардса – Андерсона, аналогичной модели SK, диапазон взаимодействия по-прежнему бесконечен. Гамильтониан для этой модели описывается следующим образом:

H = - ∑ i 1 < i 2 < ⋯ < i r J i 1 … i r S i 1 ⋯ S i r {\displaystyle H=-\sum _{i_{1}

H = - \ sum_ {i_1 <i_2 <\ cdots <i_r} J_ {i_1 \ dots i_r} S_ {i_1} \ cdots S_ {i_r}

где $J i 1… ir, S i 1,…, S ir {\ displaystyle J_ {i_ {1} \ dots i_ {r}}, S_ {i_ {1}}, \ dots, S_ {i_ {r}}}$ $J_ {i_1 \ dots i_r}, S_ { i_1}, \ точки, S_ {i_r}$ имеют те же значения, что и в модели EA. Предел $r → ∞ {\ displaystyle r \ to \ infty}$ $r \ to \ infty$ этой модели известен как модель случайной энергии. В этом пределе можно видеть, что вероятность существования спинового стекла в конкретном состоянии зависит только от энергии этого состояния, а не от отдельных спиновых конфигураций в нем. Обычно для решения этой модели предполагается гауссово распределение магнитных связей по решетке. Ожидается, что любое другое распределение даст такой же результат, как следствие центральной предельной теоремы. Функция распределения Гаусса со средним значением $J 0 N {\ displaystyle {\ frac {J_ {0}} {N}}}$ ${\ displaystyle {\ frac {J_ {0}} {N} }}$ и дисперсией $J 2 N {\ displaystyle {\ frac {J ^ {2}} {N}}}$ ${\ displaystyle {\ frac {J ^ {2}} {N}}}$ , задается как:

P (J i 1 ⋯ ir) = N r - 1 J 2 π r! ехр ⁡ {- N r - 1 J 2 r! (J я 1 ⋯ ir - J 0 р! 2 N r - 1)} {\ displaystyle P \ left (J_ {i_ {1} \ cdots i_ {r}} \ right) = {\ sqrt {\ frac {N ^ {r-1}} {J ^ {2} \ pi r!}}} \ exp \ left \ {- {\ frac {N ^ {r-1}} {J ^ {2} r!}} \ left (J_ {i_ {1} \ cdots i_ {r}} - {\ frac {J_ {0} r!} {2N ^ {r-1}}} \ right) \ right \}}

{\ displaystyle P \ left (J_ {i_ {1} \ cdots i_ {r}} \ right) = {\ sqrt {\ frac {N ^ {r-1}} {J ^ {2} \ pi r!}}} \ exp \ left \ {- {\ frac {N ^ {r-1}} {J ^ {2} r!}} \ left (J_ {i_ {1} \ cdots i_ {r}} - {\ frac {J_ {0} r!} {2N ^ {r- 1}}} \ right) \ right \}}

Порядок параметры для этой системы задаются намагниченностью $m {\ displaystyle m}$ $m$ и двухточечной корреляцией спинов между спинами в одном и том же месте $q {\ displaystyle q}$ $q$ , в двух разных репликах, которые такие же, как у модели SK. Эта модель с бесконечным радиусом действия может быть явно решена для свободной энергии в терминах $m {\ displaystyle m}$ $m$ и $q {\ displaystyle q}$ $q$ в предположении симметрии реплики, а также нарушение симметрии 1-реплики.

β f = 1 4 β 2 J 2 qr - 1 2 r β 2 J 2 qr - 1 4 β 2 J 2 + 1 2 β J 0 rmr + 1 4 2 π r β 2 J 2 qr - 1 + ∫ exp ⁡ (- 1 2 z 2) log ⁡ (2 ch ⁡ (β J z 1 2 rqr - 1 + 1 2 β J 0 rmr - 1)) dz { \ displaystyle {\ begin {align} \ beta f = {} {\ frac {1} {4}} \ beta ^ {2} J ^ {2} q ^ {r} - {\ frac {1} {2 }} r \ beta ^ {2} J ^ {2} q ^ {r} - {\ frac {1} {4}} \ beta ^ {2} J ^ {2} + {\ frac {1} {2 }} \ beta J_ {0} rm ^ {r} + {\ frac {1} {4 {\ sqrt {2 \ pi}}}} r \ beta ^ {2} J ^ {2} q ^ {r- 1} + {} \\ \ int \ exp \ left (- {\ frac {1} {2}} z ^ {2} \ right) \ log \ left (2 \ cosh \ left (\ beta Jz {\ sqrt {{\ frac {1} {2}} rq ^ {r-1}}} + {\ frac {1} {2}} \ beta J_ {0} rm ^ {r-1} \ right) \ right) \, \ mathrm {d} z \ end {align}}}

{\ displaystyle {\ begin {align} \ beta f = {} {\ frac {1} {4}} \ beta ^ {2} J ^ {2} q ^ {r} - {\ frac {1} {2}} r \ beta ^ {2} J ^ {2} q ^ {r} - {\ frac {1} {4}} \ beta ^ {2} J ^ {2} + {\ frac {1} {2}} \ beta J_ {0} rm ^ {r} + {\ frac {1} {4 {\ sqrt {2 \ pi}}}} r \ beta ^ {2} J ^ {2} q ^ {r-1} + {} \\ \ int \ exp \ left (- {\ frac {1} {2}} z ^ {2} \ right) \ log \ left (2 \ ch \ left (\ beta Jz {\ sqrt {{\ frac {1} {2}} rq ^ {r-1}}} + {\ frac {1} {2}} \ beta J_ {0} rm ^ {r-1} \ right) \ right) \, \ mathrm {d} z \ end {выровнено} }}

Неэргодическое поведение и приложения

Термодинамическая система эргодична, если для любого (равновесного) экземпляра системы em, он в конечном итоге посещает любое другое возможное (равновесное) состояние (с той же энергией). Одной из характеристик спиновых стеклянных систем является то, что ниже температуры замерзания $T f {\ displaystyle T _ {\ text {f}}}$ ${\ displaystyle T _ {\ text {f}}}$ экземпляры оказываются в ловушке «неэргодического» набора состояний : система может колебаться между несколькими состояниями, но не может переходить в другие состояния с эквивалентной энергией. Интуитивно можно сказать, что система не может выйти из глубоких минимумов иерархически неупорядоченного энергетического ландшафта; расстояния между минимумами задаются ультраметрическим с высокими энергетическими барьерами между минимумами. Подсчитывается количество состояний, доступных из данного экземпляра, то есть количество состояний, которые участвуют в основном состоянии.

. Для физических систем, таких как разбавленный марганец в меди, температура замерзания обычно равна низкое, как 30 кельвинов (-240 ° C), и поэтому магнетизм спинового стекла, кажется, практически не имеет применения в повседневной жизни. Однако неэргодические состояния и сложные энергетические ландшафты весьма полезны для понимания поведения определенных нейронных сетей, включая сети Хопфилда, а также многих проблем в компьютере. наука оптимизация и генетика.

Самоиндуцированное спиновое стекло

В 2020 году исследователи-физики из Университета Радбауд и Университета Упсалы объявили, что они наблюдали поведение, известное как самоиндуцированное спиновое стекло в атомной структуре неодима. Один из исследователей объяснил: «... мы специалисты в сканирующей туннельной микроскопии. Она позволяет нам видеть структуру отдельных атомов, и мы можем различать северный и южный полюса атомов. С помощью этого Благодаря прогрессу в области высокоточной визуализации мы смогли обнаружить поведение неодима, потому что смогли выявить невероятно малые изменения в магнитной структуре ». Неодим ведет себя сложным магнитным образом, который ранее не наблюдался в элементах периодической таблицы.

История поля

Подробное описание истории спиновых стекол с начала 1960-х годов до конец 1980-х годов можно найти в серии популярных статей Филипа В. Андерсона в Physics Today.

См. также

Примечания

Ссылки

Литература

Эдвардс, СФ; Андерсон, П.В. (1975), "Теория спиновых стекол", Journal of Physics F: Metal Physics, 5 (5): 965–974, Bibcode : 1975JPhF.... 5..965E, doi : 10.1088 / 0305-4608 / 5/5/017. [1]
Шеррингтон, Дэвид; Киркпатрик, Скотт (1975), "Решаемая модель спин-стекла", Physical Review Letters, 35 (26): 1792–1796, Bibcode : 1975PhRvL.. 35.1792S, doi : 10.1103 / PhysRevLett.35.1792. Обзор Papercore http://papercore.org/Sherrington1975
Nordblad, P.; Lundgren, L.; Сандлунд, Л. (1986), «Связь между релаксацией охлажденного нулевого поля и термоостаточной намагниченностью в спиновых стеклах», Journal of Magnetism and Magnetic Materials, 54 : 185–186, Bibcode : 1986JMMM... 54..185N, doi : 10.1016 / 0304-8853 (86) 90543-3.
Биндер, К. ; Янг, AP (1986), «Спиновые очки: экспериментальные факты, теоретические концепции и открытые вопросы», Reviews of Modern Physics, 58 (4): 801–976, Bibcode : 1986RvMP... 58..801B, doi : 10.1103 / RevModPhys.58.801.
Bryngelson, Joseph D.; Уолинс, Питер Г. (1987), "Спиновые очки и статистическая механика сворачивания белков", Proceedings of the National Academy of Sciences, 84(21): 7524–7528, Bibcode : 1987PNAS... 84.7524B, doi : 10.1073 / pnas.84.21.7524, PMC 299331, PMID 3478708.
Фишер, KH; Герц, Дж. А. (1991), Spin Glasses, Cambridge University Press.
Mezard, Marc; Паризи, Джорджио ; Вирасоро, Мигель Анхель (1987), Теория спинового стекла и не только, Сингапур: World Scientific, ISBN 978-9971-5-0115-0.
Mydosh, JA (1995), Spin Glasses, Taylor Francis.
Parisi, G. (1980), «Параметр порядка для спиновых стекол: функция на интервале 0-1» (PDF), J. Phys. A: Математика. Gen., 13 (3): 1101–1112, Bibcode : 1980JPhA... 13.1101P, doi : 10.1088 / 0305-4470 / 13/3/042 Резюме Papercore http://papercore.org/Parisi1980.
Talagrand, Michel (2000), «Реплика нарушение симметрии и экспоненциальные неравенства для Шеррингтона – Киркпатрика модель », Annals of Probability, 28 (3): 1018–1062, doi : 10.1214 / aop / 1019160325, JSTOR 2652978.
.Guerra, F.; Тонинелли, Флорида (2002), «Термодинамический предел в моделях спинового стекла среднего поля», Communications in Mathematical Physics, 230 (1): 71–79, arXiv : cond-mat / 0204280, Bibcode : 2002CMaPh.230... 71G, doi : 10.1007 / s00220-002-0699- y
Аминов Т.Г.; Новоторцев, В.Н. (2014), «Спиновые стекла в твердых растворах на основе Cu 0,5 Fe 0,5 Cr2S4», Неорганические материалы, 50 (13): 1343–00, doi : 10.1134 / s0020168514130020, ISSN 0020-1685

Внешние ссылки