Сеть Хопфилда

Хопфилда сеть (или Изинга модель нейронной сети или Изинг-Ленца-модели Литтла) является одной из форм рецидивирующих искусственной нейронной сети и типа спинового стекла системы популяризировал Хопфилд в 1982 году, как было описано ранее Литтл в 1974 году на основе Ernst Работа Изинга с Вильгельмом Ленцем над моделью Изинга. Сети Хопфилда служат в качестве систем памяти с адресной («ассоциативной») памятью с бинарными пороговыми узлами или с непрерывными переменными. Сети Хопфилда также предоставляют модель для понимания человеческой памяти.

СОДЕРЖАНИЕ

• 1 Происхождение
• 2 Структура
• 3 Обновление
  • 3.1. Нейроны «притягивают или отталкивают друг друга» в пространстве состояний
• 4 Принципы работы дискретных и непрерывных сетей Хопфилда
• 5 Энергия
• 6 Сеть Хопфилда в оптимизации
• 7 Инициализация и запуск
• 8 Обучение
  • 8.1 Правила обучения
  • 8.2 Правило обучения Hebbian для сетей Хопфилда
  • 8.3 Правило обучения аиста
• 9 ложных узоров
• 10 Вместимость
• 11 Человеческая память
• 12 Плотная ассоциативная память или современная сеть Хопфилда
  • 12.1 Дискретные переменные
  • 12.2 Непрерывные переменные
  • 12.3 Связь с классической сетью Хопфилда с непрерывными переменными
  • 12.4 Общая формулировка современной сети Хопфилда
  • 12.5 Иерархическая ассоциативная сеть памяти
• 13 См. Также
• 14 Ссылки
• 15 Внешние ссылки

Происхождение

Модель Изинга нейронной сети в качестве модели памяти впервые была предложена Уильямом А. Литтлом в 1974 году, что было признано Хопфилдом в его статье 1982 года. Сети с непрерывной динамикой были разработаны Хопфилдом в его статье 1984 года. В 2016 году Кротов и Хопфилд добились значительного прогресса в увеличении емкости памяти за счет изменения сетевой динамики и энергетической функции. Эта идея была далее расширена Демирджигилом и его сотрудниками в 2017 году. Непрерывная динамика моделей большой емкости памяти была развита в серии статей между 2016 и 2020 годами. Сети Хопфилда с большой емкостью памяти теперь называются плотными ассоциативными воспоминаниями или современными сетями Хопфилда.

Состав

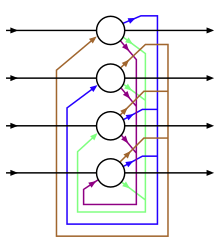Сетка Хопфилда с четырьмя звеньями

Единицы в сетях Хопфилда являются бинарными пороговыми единицами, то есть единицы принимают только два разных значения для своих состояний, и значение определяется тем, превышает ли вход единицы ее пороговое значение. Дискретные сети Хопфилда описывают отношения между бинарными (активными или неактивными) нейронами. В определенное время состояние нейронной сети описывается вектором, который записывает, какие нейроны срабатывают, в двоичном слове из N бит. ${\ displaystyle U_ {i}}$${\ displaystyle 1,2, \ ldots, i, j, \ ldots, N}$${\ displaystyle V}$

Взаимодействия между нейронами имеют единицы, которые обычно принимают значения 1 или -1, и это соглашение будет использоваться в этой статье. Однако в другой литературе могут использоваться единицы, принимающие значения 0 и 1. Эти взаимодействия «изучаются» с помощью закона ассоциации Хебба, так что для определенного состояния ${\ displaystyle w_ {ij}}$${\ Displaystyle V ^ {s}}$

${\ displaystyle w_ {ij} = V_ {i} ^ {s} V_ {j} ^ {s}}$

но. ${\ displaystyle w_ {ii} = 0}$

(Обратите внимание, что правило обучения Хебба принимает форму, когда единицы принимают значения в {0, 1}.) ${\ displaystyle w_ {ij} = (2V_ {i} ^ {s} -1) (2V_ {j} ^ {s} -1)}$

Как только сеть обучена, больше не развиваться. Если в нейронную сеть вводится новое состояние нейронов, сеть воздействует на нейроны так, что ${\ displaystyle w_ {ij}}$${\ Displaystyle V ^ {s '}}$

• ${\ Displaystyle V_ {я} ^ {s '} \ rightarrow 1}$ если ${\ displaystyle \ sum _ {j} w_ {ij} V_ {j} ^ {s '}gt; U_ {i}}$
• ${\ Displaystyle V_ {я} ^ {s '} \ rightarrow -1}$ если ${\ displaystyle \ sum _ {j} w_ {ij} V_ {j} ^ {s '} lt;U_ {i}}$

где - пороговое значение i-го нейрона (часто принимается равным 0). Таким образом, сети Хопфилда имеют возможность «запоминать» состояния, хранящиеся в матрице взаимодействия, потому что, если новое состояние подвергается воздействию матрицы взаимодействия, каждый нейрон будет изменяться, пока не будет соответствовать исходному состоянию (см. Раздел «Обновления» ниже). ${\ displaystyle U_ {i}}$${\ Displaystyle V ^ {s '}}$${\ Displaystyle V ^ {s}}$

Соединения в сети Хопфилда обычно имеют следующие ограничения:

• ${\ displaystyle w_ {ii} = 0, \ forall i}$ (никакая единица не связана сама с собой)
• ${\ displaystyle w_ {ij} = w_ {ji}, \ forall i, j}$ (соединения симметричны)

Ограничение, что веса являются симметричными, гарантирует, что функция энергии монотонно убывает при соблюдении правил активации. Сеть с асимметричным весом может демонстрировать периодическое или хаотическое поведение; однако Хопфилд обнаружил, что это поведение ограничено относительно небольшими частями фазового пространства и не ухудшает способность сети действовать как ассоциативная система памяти с адресацией по содержанию.

Хопфилд также смоделировал нейронные сети для непрерывных значений, в которых электрический выход каждого нейрона не двоичный, а некоторое значение от 0 до 1. Он обнаружил, что этот тип сети также может сохранять и воспроизводить запомненные состояния.

Обратите внимание, что каждая пара модулей i и j в сети Хопфилда имеет соединение, которое описывается весом связности. В этом смысле сеть Хопфилда можно формально описать как полный неориентированный граф, где представляет собой набор нейронов Мак-Каллоха – Питтса и является функцией, которая связывает пары единиц с реальным значением, весом связности. ${\ displaystyle w_ {ij}}$${\ Displaystyle G = \ langle V, f \ rangle}$${\ displaystyle V}$ ${\ displaystyle f: V ^ {2} \ rightarrow \ mathbb {R}}$

Обновление

Обновление одного блока (узла на графике, имитирующем искусственный нейрон) в сети Хопфилда выполняется по следующему правилу:

${\ displaystyle s_ {i} \ leftarrow \ left \ {{\ begin {array} {ll} +1 amp; {\ text {if}} \ sum _ {j} {w_ {ij} s_ {j}} \ geq \ theta _ {i}, \\ - 1 amp; {\ text {в противном случае.}} \ end {array}} \ right.}$

куда:

• ${\ displaystyle w_ {ij}}$ - сила веса соединения от единицы j к единице i (вес соединения).
• ${\ displaystyle s_ {i}}$ состояние i-го агрегата.
• ${\ displaystyle \ theta _ {я}}$ - порог единицы i.

Обновления в сети Hopfield могут выполняться двумя разными способами:

• Асинхронный: единовременно обновляется только один модуль. Этот отряд можно выбрать случайным образом или задать заранее определенный порядок с самого начала.
• Синхронно: все блоки обновляются одновременно. Для этого требуются центральные часы в системе, чтобы поддерживать синхронизацию. Некоторые считают этот метод менее реалистичным из-за отсутствия наблюдаемых глобальных часов, влияющих на аналогичные биологические или физические системы, представляющие интерес.

Нейроны «притягивают или отталкивают друг друга» в пространстве состояний

Вес между двумя единицами оказывает сильное влияние на значения нейронов. Рассмотрим вес связи между двумя нейронами i и j. Если, правило обновления подразумевает, что: ${\ displaystyle w_ {ij}}$${\ displaystyle w_ {ij}gt; 0}$

• когда вклад j во взвешенную сумму положительный. Таким образом, j притягивается к своему значению${\ displaystyle s_ {j} = 1}$${\ displaystyle s_ {i}}$${\ displaystyle s_ {i} = 1}$
• когда вклад j во взвешенную сумму отрицательный. Затем снова подталкивается j к его значению${\ displaystyle s_ {j} = - 1}$${\ displaystyle s_ {i}}$${\ displaystyle s_ {i} = - 1}$

Таким образом, значения нейронов i и j сойдутся, если вес между ними положительный. Точно так же они разойдутся, если вес отрицательный.

Принципы работы дискретных и непрерывных сетей Хопфилда

Брук пролил свет на поведение нейрона в дискретной сети Хопфилда, когда доказал его сходимость в своей статье 1990 года. В следующей статье было дополнительно исследовано поведение любого нейрона в сетях Хопфилда как с дискретным, так и с непрерывным временем, когда соответствующая функция энергии сводится к минимуму в процессе оптимизации. Брук показывает, что нейрон j меняет свое состояние тогда и только тогда, когда он дополнительно уменьшает следующий смещенный псевдоразрез. Дискретная сеть Хопфилда минимизирует следующий смещенный псевдоразрез для синаптической весовой матрицы сети Хопфилда.

${\ Displaystyle J_ {псевдо-вырез} (к) = \ сумма _ {я \ in C_ {1} (k)} \ sum _ {j \ in C_ {2} (k)} w_ {ij} + \ sum _ {j \ in C_ {1} (k)} {\ theta _ {j}}}$

где и представляет собой набор нейронов, которые имеют -1 и +1, соответственно, в момент времени. Для получения дополнительной информации см. Недавнюю статью. ${\ Displaystyle C_ {1} (к)}$${\ Displaystyle C_ {2} (к)}$${\ displaystyle k}$

Сеть Хопфилда с дискретным временем всегда минимизирует точно следующий псевдоразрез

${\ displaystyle U (k) = \ sum _ {i = 1} ^ {N} \ sum _ {j = 1} ^ {N} w_ {ij} (s_ {i} (k) -s_ {j} ( k)) ^ {2} +2 \ sum _ {j = 1} ^ {N} \ theta _ {j} s_ {j} (k)}$

Сеть Хопфилда с непрерывным временем всегда минимизирует верхнюю границу следующего взвешенного разреза

${\ displaystyle V (t) = \ sum _ {i = 1} ^ {N} \ sum _ {j = 1} ^ {N} w_ {ij} (f (s_ {i} (t)) - f ( s_ {j} (t)) ^ {2} +2 \ sum _ {j = 1} ^ {N} \ theta _ {j} f (s_ {j} (t))}$

где - сигмоидальная функция с нулевым центром. ${\ Displaystyle е (\ cdot)}$

С другой стороны, сложная сеть Хопфилда обычно стремится минимизировать так называемое «срезание тени» комплексной весовой матрицы сети.

Энергия

Энергетический ландшафт сети Хопфилда, подчеркивающий текущее состояние сети (в гору), состояние аттрактора, к которому она в конечном итоге сойдется, минимальный уровень энергии и область притяжения, заштрихованная зеленым. Обратите внимание на то, что обновление сети Хопфилда всегда идет на спад в энергетике.

Сети Хопфилда имеют скалярное значение, связанное с каждым состоянием сети, называемое «энергией» E сети, где:

${\ displaystyle E = - {\ frac {1} {2}} \ sum _ {i, j} w_ {ij} s_ {i} s_ {j} + \ sum _ {i} \ theta _ {i} s_ {я}}$

Это количество называется «энергией», потому что оно либо уменьшается, либо остается неизменным при обновлении сетевых модулей. Кроме того, при повторном обновлении сеть в конечном итоге сходится к состоянию, которое является локальным минимумом в функции энергии (которая считается функцией Ляпунова ). Таким образом, если состояние является локальным минимумом в функции энергии, это стабильное состояние для сети. Обратите внимание, что эта функция энергии принадлежит к общему классу моделей в физике под названием модели Изинга ; они, в свою очередь, являются частным случаем сетей Маркова, поскольку ассоциированная вероятностная мера, мера Гиббса, обладает свойством Маркова.

Сеть Хопфилда в оптимизации

Хопфилд и Танк представили сетевое приложение Хопфилда для решения классической задачи коммивояжера в 1985 году. С тех пор сеть Хопфилда широко используется для оптимизации. Идея использования сети Хопфилда в задачах оптимизации проста: если ограниченная / неограниченная функция затрат может быть записана в форме энергетической функции Хопфилда E, то существует сеть Хопфилда, точки равновесия которой представляют решения для ограниченной / неограниченной оптимизации. проблема. Минимизация функции энергии Хопфилда минимизирует целевую функцию и удовлетворяет ограничениям, так как ограничения «встроены» в синаптические веса сети. Хотя включение ограничений оптимизации в синаптические веса наилучшим образом является сложной задачей, на самом деле многие различные сложные задачи оптимизации с ограничениями в различных дисциплинах были преобразованы в функцию энергии Хопфилда: системы ассоциативной памяти, аналого-цифровое преобразование, проблема планирования рабочего места, квадратичное назначение и другие связанные с ней NP-полные проблемы, проблема распределения каналов в беспроводных сетях, проблема маршрутизации в мобильной сети ad-hoc, восстановление изображения, идентификация системы, комбинаторная оптимизация и т. д., и это лишь некоторые из них. Более подробную информацию можно найти, например, в статье.

Инициализация и запуск

Инициализация сетей Хопфилда выполняется путем установки значений единиц на желаемый стартовый образец. Затем выполняются повторные обновления до тех пор, пока сеть не сойдется к шаблону аттрактора. Сходимость обычно обеспечивается, поскольку Хопфилд доказал, что аттракторы этой нелинейной динамической системы стабильны, а не периодичны или хаотичны, как в некоторых других системах. Следовательно, в контексте сетей Хопфилда шаблон аттрактора - это окончательное стабильное состояние, шаблон, который не может изменить какое-либо значение в нем при обновлении.

Обучение

Тренировка сети Хопфилда включает в себя снижение энергии состояний, которые сеть должна «запоминать». Это позволяет сети служить системой памяти с адресацией по содержанию, то есть сеть будет сходиться к «запомненному» состоянию, если ей дана только часть состояния. Сеть может использоваться для восстановления после искаженного ввода до обученного состояния, которое наиболее похоже на этот ввод. Это называется ассоциативной памятью, потому что она восстанавливает воспоминания на основе сходства. Например, если мы обучаем сеть Хопфилда с пятью модулями так, чтобы состояние (1, −1, 1, −1, 1) было минимумом энергии, и мы даем сети состояние (1, −1, −1, −1, 1) он сходится к (1, −1, 1, −1, 1). Таким образом, сеть правильно обучается, когда энергия состояний, которую она должна запомнить, является локальным минимумом. Обратите внимание, что, в отличие от тренировки персептрона, пороговые значения нейронов никогда не обновляются.

Правила обучения

Существуют различные правила обучения, которые можно использовать для хранения информации в памяти сети Хопфилда. Желательно, чтобы правило обучения обладало обоими из следующих двух свойств:

• Локальный: правило обучения является локальным, если каждый вес обновляется с использованием информации, доступной нейронам по обе стороны от соединения, которое связано с этим конкретным весом.
• Пошаговый: новые шаблоны можно изучать без использования информации из старых шаблонов, которые также использовались для обучения. То есть, когда для обучения используется новый шаблон, новые значения весов зависят только от старых значений и от нового шаблона.

Эти свойства желательны, поскольку удовлетворяющее им правило обучения более правдоподобно с биологической точки зрения. Например, поскольку человеческий мозг постоянно изучает новые концепции, можно предположить, что человеческое обучение идет постепенно. Система обучения, которая не была инкрементальной, обычно обучалась только один раз с огромным пакетом обучающих данных.

Правило обучения Hebbian для сетей Хопфилда

Теория Хебба была введена Дональдом Хебба в 1949 году, для того, чтобы объяснить «ассоциативное обучение», в котором одновременно активацию нейронных клеток приводят к выраженному увеличению синаптической силы между этими клетками. Это часто резюмируется как «Нейроны, которые срабатывают вместе, соединяются вместе. Нейроны, которые срабатывают не синхронно, не могут связываться».

Правило Hebbian является одновременно локальным и инкрементным. Для сетей Хопфилда при изучении бинарных паттернов это реализуется следующим образом: ${\ displaystyle n}$

${\ displaystyle w_ {ij} = {\ frac {1} {n}} \ sum _ {\ mu = 1} ^ {n} \ epsilon _ {i} ^ {\ mu} \ epsilon _ {j} ^ { \ mu}}$

где представляет бит i из шаблона. ${\ displaystyle \ epsilon _ {я} ^ {\ mu}}$${\ displaystyle \ mu}$

Если биты, соответствующие нейронам i и j, равны по шаблону, то произведение будет положительным. Это, в свою очередь, положительно повлияет на вес, и значения i и j будут иметь тенденцию становиться равными. Обратное происходит, если биты, соответствующие нейронам i и j, различны. ${\ displaystyle \ mu}$${\ displaystyle \ epsilon _ {я} ^ {\ mu} \ epsilon _ {j} ^ {\ mu}}$${\ displaystyle w_ {ij}}$

Правило обучения аиста

Это правило было введено Амосом Сторки в 1997 году и является одновременно локальным и постепенным. Сторки также показал, что сеть Хопфилда, обученная с использованием этого правила, имеет большую пропускную способность, чем соответствующая сеть, обученная с использованием правила Хеббиана. Говорят, что весовая матрица аттракторной нейронной сети подчиняется правилу обучения Сторки, если она подчиняется:

${\ displaystyle w_ {ij} ^ {\ nu} = w_ {ij} ^ {\ nu -1} + {\ frac {1} {n}} \ epsilon _ {i} ^ {\ nu} \ epsilon _ { j} ^ {\ nu} - {\ frac {1} {n}} \ epsilon _ {i} ^ {\ nu} h_ {ji} ^ {\ nu} - {\ frac {1} {n}} \ эпсилон _ {j} ^ {\ nu} h_ {ij} ^ {\ nu}}$

где - форма локального поля на нейроне i. ${\ displaystyle h_ {ij} ^ {\ nu} = \ sum _ {k = 1 ~: ~ i \ neq k \ neq j} ^ {n} w_ {ik} ^ {\ nu -1} \ epsilon _ { k} ^ {\ nu}}$

Это правило обучения является локальным, поскольку синапсы учитывают только нейроны по бокам. Правило использует больше информации из шаблонов и весов, чем обобщенное правило Хебба, из-за эффекта локального поля.

Ложные узоры

Паттерны, которые сеть использует для обучения (называемые состояниями поиска), становятся аттракторами системы. Повторные обновления в конечном итоге приведут к сходимости к одному из состояний поиска. Однако иногда сеть сходится к ложным шаблонам (отличным от шаблонов обучения). Энергия в этих ложных паттернах также является локальным минимумом. Для каждого сохраненного шаблона x отрицание -x также является ложным шаблоном.

Ложное состояние также может быть линейной комбинацией нечетного числа состояний поиска. Например, при использовании 3 паттернов можно получить следующее ложное состояние: ${\ displaystyle \ mu _ {1}, \ mu _ {2}, \ mu _ {3}}$

${\ displaystyle \ epsilon _ {i} ^ {\ rm {mix}} = \ pm \ operatorname {sgn} (\ pm \ epsilon _ {i} ^ {\ mu _ {1}} \ pm \ epsilon _ {i } ^ {\ mu _ {2}} \ pm \ epsilon _ {i} ^ {\ mu _ {3}})}$

Ложные паттерны с четным числом состояний не могут существовать, так как они могут в сумме равняться нулю.

Емкость

Емкость сети в сетевой модели Хопфилда определяется количеством нейронов и связями в данной сети. Следовательно, количество воспоминаний, которые могут быть сохранены, зависит от нейронов и связей. Кроме того, было показано, что точность отзыва между векторами и узлами составляла 0,138 (примерно 138 векторов можно вызвать из памяти на каждые 1000 узлов) (Hertz et al., 1991). Следовательно, очевидно, что при попытке сохранить большое количество векторов произойдет много ошибок. Когда модель Хопфилда не запоминает правильный паттерн, возможно, что произошло вторжение, поскольку семантически связанные элементы имеют тенденцию вводить в заблуждение человека, и происходит запоминание неправильного паттерна. Таким образом, сетевая модель Хопфилда при извлечении путает один сохраненный элемент с другим. Идеальные отзывы и высокая емкость,gt; 0,14, могут быть загружены в сеть с помощью метода обучения Storkey; ETAM, эксперименты ETAM также проводятся. Позднее были разработаны дополнительные модели, вдохновленные сетью Хопфилда, для увеличения предела хранения и уменьшения количества ошибок при извлечении, при этом некоторые из них были способны к однократному обучению.

Емкость хранилища может быть задана как где - количество нейронов в сети. ${\ displaystyle C \ cong {\ frac {n} {2 \ log _ {2} n}}}$${\ displaystyle n}$

Человеческая память

Модель Хопфилда учитывает ассоциативную память за счет включения векторов памяти. Векторы памяти можно использовать немного, и это вызовет поиск наиболее похожего вектора в сети. Однако мы выясним, что из-за этого процесса могут происходить вторжения. В ассоциативной памяти для сети Хопфилда есть два типа операций: автоассоциация и гетероассоциация. Первый - когда вектор связан сам с собой, а второй - когда два разных вектора связаны в хранилище. Кроме того, оба типа операций можно хранить в одной матрице памяти, но только если данная матрица представления не является одной или другой из операций, а скорее является их комбинацией (автоассоциативной и гетероассоциативной). Важно отметить, что сетевая модель Хопфилда использует то же правило обучения, что и правило обучения Хебба (1949), которое в основном пытается показать, что обучение происходит в результате усиления весов, когда происходит активность.

Риццуто и Кахана (2001) смогли показать, что модель нейронной сети может учитывать повторение при точности отзыва путем включения алгоритма вероятностного обучения. Во время процесса поиска обучения не происходит. В результате веса сети остаются фиксированными, показывая, что модель может переключаться с этапа обучения на этап отзыва. Добавив контекстный дрейф, они смогли показать быстрое забвение, которое происходит в модели Хопфилда во время задания на вызов. Вся сеть способствует изменению активации любого отдельного узла.

Динамическое правило Маккаллоха и Питтса (McCulloch and Pitts, 1943), которое описывает поведение нейронов, делает это таким образом, чтобы показать, как активации нескольких нейронов отображаются на активацию скорости возбуждения нового нейрона и как веса нейронов усиливают синаптические связи между новым активированным нейроном (и теми, которые его активировали). Хопфилд использовал динамическое правило Маккаллоха – Питтса, чтобы показать, как поиск возможен в сети Хопфилда. Однако важно отметить, что Хопфилд делал это постоянно. Хопфилд будет использовать нелинейную функцию активации вместо использования линейной функции. Таким образом, это создаст динамическое правило Хопфилда, и с его помощью Хопфилд смог показать, что с помощью нелинейной функции активации динамическое правило всегда будет изменять значения вектора состояния в направлении одного из сохраненных шаблонов.

Плотная ассоциативная память или современная сеть Хопфилда

Сети Хопфилда - это рекуррентные нейронные сети с динамическими траекториями, сходящимися к состояниям аттрактора с фиксированной точкой и описываемые функцией энергии. Состояние каждого модельного нейрона определяется зависящей от времени переменной, которая может быть дискретной или непрерывной. Полная модель описывает математику того, как будущее состояние активности каждого нейрона зависит от известной текущей или предыдущей активности всех нейронов. ${\ textstyle i}$${\ displaystyle V_ {i}}$

В исходной модели ассоциативной памяти Хопфилда переменные были двоичными, а динамика описывалась однократным обновлением состояния нейронов. Была определена функция энергии, квадратичная по величине, и динамика заключалась в изменении активности каждого отдельного нейрона только в том случае, если это снизит общую энергию системы. Эта же идея была распространена на случай, когда она является непрерывной переменной, представляющей выходной сигнал нейрона, и является монотонной функцией входного тока. Динамика стала выражаться в виде набора дифференциальных уравнений первого порядка, для которых «энергия» системы всегда уменьшалась. Энергия в непрерывном случае имеет один член, который является квадратичным по (как в бинарной модели), и второй член, который зависит от функции усиления (функция активации нейрона). Обладая многими желательными свойствами ассоциативной памяти, обе эти классические системы страдают от небольшой емкости памяти, которая линейно масштабируется с количеством входных функций. ${\ displaystyle V_ {i}}$${\ displaystyle i}$${\ displaystyle V_ {i}}$${\ displaystyle i}$${\ displaystyle V_ {i}}$${\ displaystyle V_ {i}}$

Плотные ассоциативные воспоминания (также известные как современные сети Хопфилда) - это обобщения классических сетей Хопфилда, которые нарушают линейное масштабное соотношение между количеством входных функций и количеством сохраненных воспоминаний. Это достигается за счет введения более сильных нелинейностей (либо в функции энергии, либо в функциях активации нейронов), что приводит к сверхлинейной (даже экспоненциальной) емкости памяти в зависимости от количества функциональных нейронов. Сеть по-прежнему требует достаточного количества скрытых нейронов.

Ключевая теоретическая идея, лежащая в основе современных сетей Хопфилда, заключается в использовании энергетической функции и правила обновления, которое более резко выражено вокруг хранимых воспоминаний в пространстве конфигураций нейронов по сравнению с классической сетью Хопфилда.

Дискретные переменные

Простой пример современной сети Хопфилда можно записать в терминах двоичных переменных, которые представляют активное и неактивное состояние модельного нейрона.${\ displaystyle V_ {i}}$${\ displaystyle V_ {i} = + 1}$${\ displaystyle V_ {i} = - 1}$${\ displaystyle i}$

$${\ displaystyle E = - \ sum \ limits _ {\ mu = 1} ^ {N _ {\ text {mem}}} F {\ Big (} \ sum \ limits _ {i = 1} ^ {N_ {f} } \ xi _ {\ mu i} V_ {i} {\ Big)}}$$ В этой формуле веса представляют собой матрицу векторов памяти (индекс перечисляет различные воспоминания, а индекс перечисляет содержимое каждой памяти, соответствующей -й характеристическому нейрону), а функция является быстрорастущей нелинейной функцией. Правило обновления для отдельных нейронов (в асинхронном случае) можно записать в следующем виде${\ textstyle \ xi _ {\ му я}}$${\ displaystyle \ mu = 1... N _ {\ text {mem}}}$${\ displaystyle i = 1... N_ {f}}$${\ displaystyle i}$${\ Displaystyle F (х)}$ $${\ Displaystyle V_ {я} ^ {(t + 1)} = Знак {\ bigg [} \ sum \ limits _ {\ mu = 1} ^ {N _ {\ text {mem}}} {\ bigg (} F {\ Big (} \ xi _ {\ mu i} + \ sum \ limits _ {j \ neq i} \ xi _ {\ mu j} V_ {j} ^ {(t)} {\ Big)} - F {\ Big (} - \ xi _ {\ mu i} + \ sum \ limits _ {j \ neq i} \ xi _ {\ mu j} V_ {j} ^ {(t)} {\ Big)} { \ bigg)} {\ bigg]}}$$ в котором говорится, что для вычисления обновленного состояния -го нейрона сеть сравнивает две энергии: энергию сети с -м нейроном в состоянии ВКЛ и энергию сети с -м нейроном в состоянии ВЫКЛ., учитывая состояния оставшегося нейрона. Обновленное состояние -го нейрона выбирает состояние с наименьшей из двух энергий. ${\ textstyle i}$${\ displaystyle i}$${\ displaystyle i}$${\ displaystyle i}$

В предельном случае, когда нелинейная функция энергии является квадратичной, эти уравнения сводятся к знакомой функции энергии и правилу обновления для классической двоичной сети Хопфилда. ${\ Displaystyle F (х) = х ^ {2}}$

Емкость памяти этих сетей может быть рассчитана для случайных двоичных шаблонов. Для функции мощности и энергии максимальное количество запоминающих устройств, которые могут быть сохранены и извлечены из этой сети без ошибок, определяется выражением${\ Displaystyle F (х) = х ^ {п}}$

$${\ displaystyle N _ {\ text {mem}} ^ {max} \ приблизительно {\ frac {1} {2 (2n-3) !!}} {\ frac {N_ {f} ^ {n-1}} { \ ln (N_ {f})}}}$$ Для экспоненциальной энергетической функции емкость памяти экспоненциально зависит от количества характерных нейронов.${\ textstyle F (x) = e ^ {x}}$ $${\ displaystyle N _ {\ text {mem}} ^ {max} \ приблизительно 2 ^ {N_ {f} / 2}}$$ Рис.1 Пример непрерывной современной сети Хопфилда с характерными нейронами и нейронами памяти (скрытыми) с симметричными синаптическими связями между ними.${\ textstyle N_ {f} = 5}$${\ displaystyle N _ {\ text {mem}} = 11}$

Непрерывные переменные

Современные сети Хопфилда или плотная ассоциативная память лучше всего можно понять в непрерывных переменных и непрерывном времени. Рассмотрим архитектуру сети, показанную на рисунке 1, и уравнения эволюции состояний нейрона.

$${\ displaystyle {\ begin {cases} \ tau _ {f} {\ frac {dx_ {i}} {dt}} = \ sum \ limits _ {\ mu = 1} ^ {N_ {h}} \ xi _ {i \ mu} f _ {\ mu} -x_ {i} + I_ {i} \\\ tau _ {h} {\ frac {dh _ {\ mu}} {dt}} = \ sum \ limits _ {i = 1} ^ {N_ {f}} \ xi _ {\ mu i} g_ {i} -h _ {\ mu} \ end {case}}}$$

( 1)

где токи характерных нейронов обозначены, а токи нейронов памяти обозначены ( обозначает скрытые нейроны). Между нейронами признаков или нейронами памяти нет синаптических связей. Матрица обозначает силу синапсов от функционального нейрона к нейрону памяти. Предполагается, что синапсы являются симметричными, так что одно и то же значение характеризует другой физический синапс от нейрона памяти до особенного нейрона. Выходы нейронов памяти и характерных нейронов обозначены и, которые являются нелинейными функциями соответствующих токов. В общем, эти выходы могут зависеть от токов всех нейронов в этом слое, так что и. Эти функции активации удобно определить как производные от функций Лагранжа для двух групп нейронов${\ textstyle x_ {i}}$${\ displaystyle h _ {\ mu}}$${\ displaystyle h}$${\ Displaystyle \ хи _ {\ му я}}$${\ displaystyle i}$${\ displaystyle \ mu}$${\ displaystyle \ mu}$${\ displaystyle i}$${\ displaystyle f _ {\ mu}}$${\ displaystyle g_ {i}}$${\ Displaystyle е _ {\ му} = е (\ {ч _ {\ му} \})}$${\ textstyle g_ {i} = g (\ {x_ {i} \})}$

$${\ displaystyle f _ {\ mu} = {\ frac {\ partial L_ {h}} {\ partial h _ {\ mu}}}, \ \ \ \ {\ text {и}} \ \ \ \ g_ {i} = {\ frac {\ partial L_ {v}} {\ partial x_ {i}}}}$$

( 2)

Таким образом, конкретная форма уравнений для состояний нейрона полностью определяется после задания функций Лагранжа. Наконец, постоянные времени для двух групп нейронов обозначены и, это входной ток в сеть, который может управляться представленными данными. ${\ displaystyle \ tau _ {f}}$${\ displaystyle \ tau _ {h}}$${\ displaystyle I_ {i}}$

Рис.2. Эффективная теория характерных нейронов для различных распространенных вариантов функций Лагранжа. Модель A сводится к моделям, изучаемым в зависимости от выбора функции активации, модель B сводится к модели, изучаемой в, модель C сводится к модели.

Общие системы нелинейных дифференциальных уравнений могут иметь много сложного поведения, которое может зависеть от выбора нелинейностей и начальных условий. Однако для сетей Хопфилда это не так - динамические траектории всегда сходятся к состоянию аттрактора с неподвижной точкой. Это свойство достигается, потому что эти уравнения специально разработаны так, чтобы они имели основную функцию энергии

$${\ displaystyle E (t) = {\ Big [} \ sum \ limits _ {i = 1} ^ {N_ {f}} (x_ {i} -I_ {i}) g_ {i} -L_ {x} {\ Big]} + {\ Big [} \ sum \ limits _ {\ mu = 1} ^ {N_ {h}} h _ {\ mu} f _ {\ mu} -L_ {h} {\ Big]} - \ sum \ limits _ {\ mu, i} f _ {\ mu} \ xi _ {\ mu i} g_ {i}}$$

( 3)

Термины, сгруппированные в квадратные скобки, представляют преобразование Лежандра функции Лагранжа относительно состояний нейронов. Если матрицы Гессе функций Лагранжа положительно полуопределены, функция энергии гарантированно убывает на динамической траектории

$${\ displaystyle {\ frac {dE (t)} {dt}} = - \ tau _ {f} \ sum \ limits _ {i, j = 1} ^ {N_ {f}} {\ frac {dx_ {i }} {dt}} {\ frac {\ partial ^ {2} L_ {x}} {\ partial x_ {i} \ partial x_ {j}}} {\ frac {dx_ {j}} {dt}} - \ tau _ {h} \ sum \ limits _ {\ mu, \ nu = 1} ^ {N_ {h}} {\ frac {dh _ {\ mu}} {dt}} {\ frac {\ partial ^ {2 } L_ {h}} {\ partial h _ {\ mu} \ partial h _ {\ nu}}} {\ frac {dh _ {\ nu}} {dt}} \ leq 0}$$

( 4)

Это свойство позволяет доказать, что система динамических уравнений, описывающих временную эволюцию активности нейронов, в конечном итоге достигнет состояния аттрактора с фиксированной точкой.

В некоторых ситуациях можно предположить, что динамика скрытых нейронов уравновешивает в гораздо быстрее масштабе времени по сравнению с функцией нейронов. В этом случае стационарное решение второго уравнения в системе ( 1) может использоваться для выражения токов скрытых единиц через выходы характерных нейронов. Это позволяет свести общую теорию ( 1) к эффективной теории только для характерных нейронов. Полученные в результате эффективные правила обновления и энергии для различных общих выборов функций Лагранжа показаны на рисунке 2. В случае экспоненциальной функции Лагранжа с логарифмической суммой правило обновления (если применяется один раз) для состояний характерных нейронов - это механизм внимания, обычно используемый во многих современных системах ИИ (см. Ссылку для вывода этого результата из непрерывного формулировка времени). ${\ textstyle \ tau _ {h} \ ll \ tau _ {f}}$

Связь с классической сетью Хопфилда с непрерывными переменными

Классическую формулировку непрерывных сетей Хопфилда можно рассматривать как частный предельный случай современных сетей Хопфилда с одним скрытым слоем. Непрерывные сети Хопфилда для нейронов с градуированной реакцией обычно описываются динамическими уравнениями

$${\ displaystyle \ tau _ {f} {\ frac {dx_ {i}} {dt}} = \ sum \ limits _ {j = 1} ^ {N_ {f}} T_ {ij} V_ {j} -x_ {i} + I_ {i}}$$

( 5)

и энергетическая функция

$${\ displaystyle E = - {\ frac {1} {2}} \ sum \ limits _ {i, j = 1} ^ {N_ {f}} T_ {ij} V_ {i} V_ {j} - \ sum \ limits _ {i = 1} ^ {N_ {f}} V_ {i} I_ {i} + \ sum \ limits _ {i = 1} ^ {N_ {f}} \ int \ limits ^ {V_ {i }} g ^ {- 1} (z) \, dz}$$

( 6)

где, и - обратная функция активации. Эта модель представляет собой особый предел класса моделей, который называется моделями A, со следующим выбором функций Лагранжа${\ textstyle V_ {i} = g (x_ {i})}$${\ Displaystyle г ^ {- 1} (г)}$${\ displaystyle g (x)}$

$${\ displaystyle L_ {v} = \ sum \ limits _ {i = 1} ^ {N_ {f}} \ int \ limits ^ {x_ {i}} g (x) dx, \ \ \ \ \ \ {\ text {и}} \ \ \ \ \ L_ {h} = {\ frac {1} {2}} \ sum \ limits _ {\ mu = 1} ^ {N_ {h}} h _ {\ mu} ^ {2 }}$$

( 7)

что согласно определению ( 2) приводит к активационным функциям

$${\ Displaystyle V_ {я} = г (х_ {я}), \ \ \ \ \ {\ текст {и}} \ \ \ \ f _ {\ му} = ч _ {\ му}}$$

( 8)

Если мы проинтегрируем скрытые нейроны, система уравнений ( 1) сводится к уравнениям на характерных нейронах ( 5) с, а общее выражение для энергии ( 3) сводится к эффективной энергии${\ displaystyle T_ {ij} = \ sum \ limits _ {\ mu = 1} ^ {N_ {h}} \ xi _ {\ mu i} \ xi _ {\ mu j}}$

$${\ displaystyle E = - {\ frac {1} {2}} \ sum \ limits _ {i, j = 1} ^ {N_ {f}} T_ {ij} V_ {i} V_ {j} - \ sum \ limits _ {i = 1} ^ {N_ {f}} V_ {i} I_ {i} + \ sum \ limits _ {i = 1} ^ {N_ {f}} {\ Big (} x_ {i} V_ {i} - \ int \ limits ^ {x_ {i}} g (x) dx {\ Big)}}$$

( 9)

Хотя первые два члена в уравнении ( 6) такие же, как и в уравнении ( 9), третьи члены внешне выглядят иначе. В уравнении ( 9) это преобразование Лежандра лагранжиана для характерных нейронов, а в ( 6) третий член представляет собой интеграл обратной функции активации. Тем не менее, эти два выражения фактически эквивалентны, поскольку производные функции и ее преобразование Лежандра являются функциями, обратными друг другу. Самый простой способ увидеть, что эти два члена явно равны, - это дифференцировать каждый по. Результаты этих дифференцирований для обоих выражений равны. Таким образом, два выражения равны с точностью до аддитивной константы. Это завершает доказательство того, что классическая сеть Хопфилда с непрерывными состояниями является частным предельным случаем современной сети Хопфилда ( 1) с энергией ( 3). ${\ displaystyle x_ {i}}$${\ Displaystyle х_ {я} г (х_ {я}) '}$

Общая формулировка современной сети Хопфилда

Рис.3 Схема связности современной полносвязной сети Хопфилда, состоящей из пяти нейронов. Синаптические веса описываются симметричной матрицей.${\ displaystyle W_ {IJ}}$

Биологические нейронные сети имеют большую степень неоднородности с точки зрения различных типов клеток. В этом разделе описывается математическая модель полностью связанной современной сети Хопфилда, предполагающая крайнюю степень неоднородности: каждый нейрон индивидуален. В частности, функция энергии и соответствующие динамические уравнения описаны в предположении, что каждый нейрон имеет свою собственную функцию активации и кинетическую шкалу времени. Предполагается, что сеть полностью подключена, так что каждый нейрон подключен к каждому другому нейрону с использованием симметричной матрицы весов, индексов и перечисления различных нейронов в сети, см. Рисунок 3. Самый простой способ математически сформулировать эту проблему - определить архитектуру через функцию Лагранжа, которая зависит от активности всех нейронов в сети. Функция активации для каждого нейрона определяется как частная производная лагранжиана по активности этого нейрона.${\ displaystyle W_ {IJ}}$${\ displaystyle I}$${\ displaystyle J}$${\ Displaystyle L (\ {x_ {I} \})}$

$${\ displaystyle g_ {I} = {\ frac {\ partial L} {\ partial x_ {I}}}}$$

( 10)

С биологической точки зрения это можно рассматривать как аксональный выход нейрона. В простейшем случае, когда лагранжиан является аддитивным для разных нейронов, это определение приводит к активации, которая является нелинейной функцией активности этого нейрона. Для неаддитивных лагранжианов эта функция активации может зависеть от активности группы нейронов. Например, он может содержать контрастную (softmax) или разделительную нормализацию. Динамические уравнения, описывающие временную эволюцию данного нейрона, задаются следующим образом:${\ displaystyle g_ {I}}$${\ displaystyle I}$

$${\ displaystyle \ tau _ {I} {\ frac {dx_ {I}} {dt}} = \ sum \ limits _ {J = 1} ^ {N} W_ {IJ} g_ {J} -x_ {I} }$$

( 11)

Это уравнение принадлежит к классу моделей, называемых в нейробиологии моделями скорости увольнения. Каждый нейрон собирает аксональные сигналы от всех нейронов, взвешивает их с помощью синаптических коэффициентов и производит свою собственную зависящую от времени активность. Временная эволюция имеет постоянную времени, которая, как правило, может быть разной для каждого нейрона. Эта сеть выполняет глобальную энергетическую функцию.${\ displaystyle I}$${\ displaystyle g_ {J}}$${\ displaystyle W_ {IJ}}$${\ displaystyle x_ {I}}$${\ displaystyle \ tau _ {I}}$

$${\ displaystyle E = \ sum \ limits _ {I = 1} ^ {N} x_ {I} g_ {I} -L - {\ frac {1} {2}} \ sum \ limits _ {I, J = 1} ^ {N} g_ {I} W_ {IJ} g_ {J}}$$

( 12)

где первые два члена представляют преобразование Лежандра функции Лагранжа относительно токов нейронов. Временная производная этой энергетической функции может быть вычислена на динамических траекториях, ведущих к (подробности см.)${\ displaystyle x_ {I}}$

$${\ displaystyle {\ frac {dE} {dt}} = - \ sum \ limits _ {I, K = 1} ^ {N} {\ frac {dx_ {I}} {dt}} M_ {IK} {\ frac {dx_ {K}} {dt}} \ leq 0, \ \ \ \ {\ text {where}} \ \ \ \ M_ {IK} = \ tau _ {I} {\ frac {\ partial ^ {2 } L} {\ partial x_ {I} \ partial x_ {K}}}}$$

( 13)

Последний знак неравенства имеет место при условии, что матрица (или ее симметричная часть) положительно полуопределенная. Если, в дополнение к этому, функция энергии ограничена снизу, нелинейные динамические уравнения гарантированно сходятся к состоянию аттрактора с неподвижной точкой. Преимущество формулировки этой сети в терминах функций Лагранжа состоит в том, что она позволяет легко экспериментировать с различными вариантами функций активации и различными архитектурными схемами нейронов. Для всех этих гибких вариантов условия сходимости определяются свойствами матрицы и существованием нижней границы функции энергии. ${\ displaystyle M_ {IK}}$${\ displaystyle M_ {IJ}}$

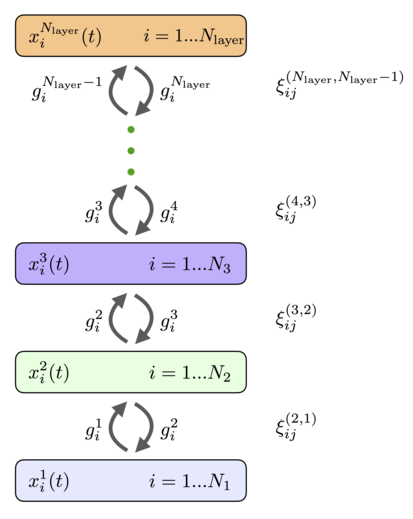Рис.4 Схема связности многоуровневой сети иерархической ассоциативной памяти. Каждый слой может иметь разное количество нейронов, разные функции активации и разные временные шкалы. Веса прямой связи и веса обратной связи равны.

Иерархическая ассоциативная сеть памяти

Нейроны могут быть организованы по слоям так, чтобы каждый нейрон в данном слое имел одинаковую функцию активации и одну и ту же динамическую шкалу времени. Если мы предположим, что нет горизонтальных связей между нейронами внутри слоя (боковые связи) и нет соединений пропущенного уровня, общая полносвязная сеть ( 11), ( 12) сводится к архитектуре, показанной на рисунке 4. Он имеет слои рекуррентно связанных нейронов с состояниями, описываемыми непрерывными переменными и функциями активации, индекс перечисляет уровни сети, а индекс перечисляет отдельные нейроны в этом слое. Функции активации могут зависеть от активности всех нейронов слоя. На каждом слое может быть разное количество нейронов. Эти нейроны периодически связаны с нейронами предыдущего и последующих слоев. Матрицы весов, которые соединяют нейроны в слоях и обозначаются (порядок верхних индексов весов такой же, как порядок нижних индексов, в приведенном выше примере это означает, что индекс перечисляет нейроны в слое, а индекс перечисляет нейроны в слое). Веса прямой связи и веса обратной связи равны. Динамические уравнения для состояний нейронов можно записать в виде${\ displaystyle N _ {\ text {layer}}}$${\ displaystyle x_ {i} ^ {A}}$${\ displaystyle g_ {i} ^ {A}}$${\ displaystyle A}$${\ displaystyle i}$${\ displaystyle N_ {A}}$${\ displaystyle A}$${\ displaystyle B}$${\ Displaystyle \ хи _ {я} ^ {(А, В)}}$${\ displaystyle i}$${\ displaystyle A}$${\ displaystyle j}$${\ displaystyle B}$

$${\ displaystyle \ tau _ {A} {\ frac {dx_ {i} ^ {A}} {dt}} = \ sum \ limits _ {j = 1} ^ {N_ {A-1}} \ xi _ { ij} ^ {(A, A-1)} g_ {j} ^ {A-1} + \ sum \ limits _ {j = 1} ^ {N_ {A + 1}} \ xi _ {ij} ^ { (A, A + 1)} g_ {j} ^ {A + 1} -x_ {i} ^ {A}}$$

( 14)

с граничными условиями

$${\ displaystyle g_ {i} ^ {0} = 0, \ \ \ \ \ {\ text {and}} \ \ \ \ g_ {i} ^ {N _ {\ text {layer}} + 1} = 0 }$$

( 15)

Основное отличие этих уравнений от обычных сетей с прямой связью - наличие второго члена, который отвечает за обратную связь от более высоких уровней. Эти нисходящие сигналы помогают нейронам нижних слоев принять решение о своей реакции на предъявляемые стимулы. Следуя общему рецепту, удобно ввести функцию Лагранжа для -го скрытого слоя, которая зависит от активности всех нейронов в этом слое. Функции активации в этом слое могут быть определены как частные производные лагранжиана${\ Displaystyle L ^ {A} (\ {x_ {i} ^ {A} \})}$${\ displaystyle A}$

$${\ displaystyle g_ {i} ^ {A} = {\ frac {\ partial L ^ {A}} {\ partial x_ {i} ^ {A}}}}$$

( 16)

С этими определениями функция энергии (Ляпунова) дается формулой

$${\ displaystyle E = \ sum \ limits _ {A = 1} ^ {N _ {\ text {layer}}} {\ Big [} \ sum \ limits _ {i = 1} ^ {N_ {A}} x_ { i} ^ {A} g_ {i} ^ {A} -L ^ {A} {\ Big]} - \ sum \ limits _ {A = 1} ^ {N _ {\ text {layer}} - 1} \ сумма \ пределы _ {i = 1} ^ {N_ {A + 1}} \ sum \ limits _ {j = 1} ^ {N_ {A}} g_ {i} ^ {A + 1} \ xi _ {ij } ^ {(A + 1, A)} g_ {j} ^ {A}}$$

( 17)

Если функции Лагранжа или, что эквивалентно, функции активации, выбраны таким образом, что гессианы для каждого слоя являются положительно полуопределенными, а общая энергия ограничена снизу, эта система гарантированно сходится к состоянию аттрактора с фиксированной точкой. Временная производная этой энергетической функции определяется выражением

$${\ displaystyle {\ frac {dE} {dt}} = - \ sum \ limits _ {A = 1} ^ {N _ {\ text {layer}}} \ tau _ {A} \ sum \ limits _ {i, j = 1} ^ {N_ {A}} {\ frac {dx_ {j} ^ {A}} {dt}} {\ frac {\ partial ^ {2} L ^ {A}} {\ partial x_ {j } ^ {A} \ partial x_ {i} ^ {A}}} {\ frac {dx_ {i} ^ {A}} {dt}} \ leq 0}$$

( 18)

Таким образом, иерархическая многоуровневая сеть действительно является аттракторной сетью с глобальной энергетической функцией. Эта сеть описывается иерархическим набором синаптических весов, которые можно узнать для каждой конкретной проблемы.

Смотрите также

• Ассоциативная память (значения)
• Автоассоциативная память
• Машина Больцмана - похожа на сеть Хопфилда, но использует отожженную выборку Гиббса вместо градиентного спуска.
• Модель динамических систем познания
• Модель Изинга
• Хеббийская теория

использованная литература

• Хебб, Д. О. (2005) [1949]. Организация поведения: нейропсихологическая теория. Психология Press. ISBN   978-1-135-63190-1.
• Герц, Джон А. (2018) [1991]. Введение в теорию нейронных вычислений. CRC Press. ISBN   978-0-429-96821-1.
• Маккаллох, WS; Питтс, WH (1943). «Логический расчет идей, присущих нервной деятельности». Вестник математической биофизики. 5 (4): 115–133. DOI : 10.1007 / BF02478259.
• Polyn, SM; Кахана, MJ (2008). «Поиск в памяти и нейронное представление контекста». Тенденции в когнитивных науках. 12 (1): 24–30. DOI : 10.1016 / j.tics.2007.10.010. PMC   2839453. PMID   18069046.
• Риццуто, DS; Кахана, MJ (2001). «Модель автоассоциативной нейронной сети парно-ассоциативного обучения». Нейронные вычисления. 13 (9): 2075–2092. CiteSeerX   10.1.1.45.7929. DOI : 10.1162 / 089976601750399317. PMID   11516358. S2CID   7675117.
• Крузе, Рудольф; Боргельт, Кристиан; Клавонн, Франк; Моуэз, Кристиан; Штайнбрехер, Маттиас; Хелд, Паскаль (2013). Вычислительный интеллект: методологическое введение. Springer. ISBN   978-1-4471-5013-8.

внешние ссылки

• Рохас, Рауль (12 июля 1996 г.). «13. Модель Хопфилда» (PDF). Нейронные сети - систематическое введение. ISBN   978-3-540-60505-8.
• Javascript сети Хопфилда
• Задача коммивояжера - JAVA-апплет нейронной сети Хопфилда
• Хопфилд, Джон (2007). «Сеть Хопфилда». Scholarpedia. 2 (5): 1977. DOI : 10,4249 / scholarpedia.1977.
• Флетчер, Тристан. "Обучение сети Хопфилда с использованием детерминированных скрытых переменных" (PDF) (Учебное пособие). Архивировано из оригинального (PDF) 05.10.2011.
• Графический интерфейс нейронной лаборатории - графический интерфейс нейронной сети Хопфилда (Python amp; gtk)