Войти
В физике конденсированного состояния термин геометрическое разочарование (или кратко: расстройство ) относится к явлению, при котором атомы стремятся придерживаться нетривиальных положений или где на регулярной кристаллической решетке возникают конфликтующие межатомные силы (каждая один предпочитает довольно простые, но разные структуры) приводят к довольно сложным структурам. Как следствие нарушения геометрии или сил, множество различных основных состояний может возникнуть при нулевой температуре, а обычное тепловое упорядочение может подавляться при более высоких температурах. Наиболее изученными примерами являются аморфные материалы, стекла или разбавленные магниты.
. Термин «разочарование» в контексте магнитных систем был введен Автор Жерар Тулуза (1977). Действительно, фрустрированные магнитные системы изучались еще раньше. Ранняя работа включает исследование модели Изинга на треугольной решетке со спинами ближайшего соседа , связанными антиферромагнитно, Г. H. Wannier, опубликовано в 1950 году. Связанные с этим особенности возникают в магнитах с конкурирующими взаимодействиями, где присутствуют как ферромагнитные, так и антиферромагнитные связи между парами спинов или магнитных моментов, причем тип взаимодействия зависит от от расстояния разделения спинов. В этом случае может возникнуть соизмеримость, такая как спиральная компоновка вращения, как это первоначально обсуждалось, в частности, А. Йошимори, Т. А. Каплан, Р. Дж. Эллиотт и другие, начиная с 1959 г., для описания результатов экспериментов с редкоземельными металлами. Возобновленный интерес к таким спиновым системам с фрустрированными или конкурирующими взаимодействиями возник примерно два десятилетия спустя, начиная с 1970-х годов, в контексте спиновых стекол и пространственно модулированных магнитных сверхструктур. В спиновых стеклах разочарование усиливается стохастическим беспорядком во взаимодействиях, что может происходить экспериментально в нестехиометрических магнитных сплавах. Тщательно проанализированные спиновые модели с фрустрацией включают модель Шеррингтона – Киркпатрика, описывающую спиновые стекла, и модель ANNNI, описывающую соизмеримость магнитных сверхструктур.
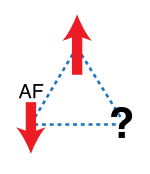Рисунок 1: Антиферромагнитно взаимодействующие спины в треугольном расположении 
Рисунок 2: Антиферромагнитно взаимодействующие спины в тетраэдрическом расположении 
Рисунок 3: Спины вдоль легкие оси тетраэдра 
Рис. 4: Разочарованные легкие вращения в тетраэдре Геометрические расстройства - важная особенность магнетизма, где они проистекают из относительного расположения спинов. Простой двумерный пример показан на рисунке 1. Три магнитных иона находятся в углах треугольника с антиферромагнитными взаимодействиями между ними; энергия минимизируется, когда каждый спин ориентирован напротив соседей. Как только первые два спина выровнены антипараллельно, третий фрустрирован, потому что его две возможные ориентации, вверх и вниз, дают одинаковую энергию. Третий спин не может одновременно минимизировать свои взаимодействия с обоими другими двумя. Поскольку этот эффект возникает для каждого спина, основное состояние является шестикратным вырожденным. Только два состояния, где все вращения вверх или вниз, имеют больше энергии.
Аналогичным образом в трех измерениях четыре спина, расположенные в тетраэдре (рис. 2), могут испытывать геометрическое расстройство. Если между спинами существует антиферромагнитное взаимодействие, то спины невозможно расположить так, чтобы все взаимодействия между спинами были антипараллельными. Существует шесть взаимодействий ближайших соседей, четыре из которых антипараллельны и, следовательно, благоприятны, но два из которых (между 1 и 2 и между 3 и 4) являются неблагоприятными. Невозможно иметь все взаимодействия благоприятно, и система расстраивается.
Геометрическое разочарование также возможно, если вращения расположены не коллинеарно образом. Если мы рассмотрим тетраэдр со спином на каждой вершине, направленным вдоль легкой оси (то есть прямо к центру тетраэдра или от него), то можно расположить четыре спина так, чтобы не было чистого спина (рис. 3). Это в точности эквивалентно наличию антиферромагнитного взаимодействия между каждой парой спинов, поэтому в этом случае нет геометрического разочарования. С этими осями возникает геометрическое разочарование, если существует ферромагнитное взаимодействие между соседями, когда энергия минимизируется параллельными спинами. Наилучшее возможное расположение показано на рисунке 4, где два вращения направлены в сторону центра, а два - в противоположную сторону. Чистый магнитный момент направлен вверх, максимизируя ферромагнитные взаимодействия в этом направлении, но левый и правый векторы компенсируются (т.е. выровнены антиферромагнитно), как и вперед, и назад. Существует три различных эквивалентных устройства с двумя выходами и двумя входами, поэтому основное состояние вырождено в три раза.
Математическое определение простое (и аналогично так называемой петле Вильсона в квантовой хромодинамике ): выражения («полные энергии» или «гамильтонианы») вида
где G - рассматриваемый график, в то время как величины I kν,kμпредставляют собой так называемые «энергии обмена» между ближайшими соседями, которые (в рассматриваемых единицах энергии) принимают значения ± 1 (математически это знаковый график ), тогда как S kν·Skμявляются внутренними произведениями скалярных или векторных спинов или псевдоспинов. Если граф G имеет квадратичные или треугольные грани P, появляются так называемые «плакеточные переменные» P W, «циклические продукты» следующего вида:
и 
соответственно,, которые также называются «продуктами разочарования». По этим произведениям нужно произвести сумму, просуммированную по всем плакетам. Результат для одной плакетки - +1 или -1. В последнем случае табличка «геометрически фрустрирована».
Можно показать, что результат имеет простую калибровочную инвариантность : он не меняется - как и другие измеримые величины, например «полная энергия» 
Здесь числа ε i и ε k являются произвольными знаками, т.е. + 1 или -1, так что измененная структура может выглядеть совершенно случайной.
Рисунок 5: Схема молекул водяного льда Хотя большинство предыдущих и текущих исследований разочарования сосредоточено на спиновых системах, это явление впервые было изучено на обычном льде. В 1936 году Джок и Стаут опубликовали «Энтропию воды и третий закон термодинамики». Теплоемкость льда от 15 K до 273 K, сообщающая об измерениях калориметром воды в процессе замерзания и испарения до высокотемпературной газовой фазы. энтропия была рассчитана путем интегрирования теплоемкости и добавления вкладов скрытой теплоты ; низкотемпературные измерения были экстраполированы к нулю с использованием недавно полученной формулы Дебая. Полученная энтропия, S 1 = 44,28 кал / (К · моль) = 185,3 Дж / (моль · К), сравнивалась с теоретическим результатом статистической механики идеального газа, S 2 = 45,10 кал / (К · моль) = 188,7 Дж / (моль · К). Эти два значения различаются на S 0 = 0,82 ± 0,05 кал / (К · моль) = 3,4 Дж / (моль · К). Этот результат был затем объяснен Линусом Полингом в превосходном приближении, который показал, что лед обладает конечной энтропией (оцениваемой как 0,81 кал / (К · моль) или 3,4 Дж / (моль · К)) при нуле. температура из-за конфигурационного беспорядка, присущего протонам во льду.
В гексагональной или кубической ледяной фазе ионы кислорода образуют тетраэдрическую структуру со связью O – O длина 2,76 Å (276 пм ), в то время как длина связи O – H составляет всего 0,96 Å (96 пм). Каждый ион кислорода (белый) окружен четырьмя ионами водорода (черный), и каждый ион водорода окружен двумя ионами кислорода, как показано на рисунке 5. Сохранение внутренней структуры молекулы H 2 O, минимальная энергия положение протона не находится посередине между двумя соседними ионами кислорода. Есть два эквивалентных положения, которые водород может занимать на линии связи O – O, дальнее и ближнее положение. Таким образом, правило приводит к фрустрации положений протона для конфигурации основного состояния: для каждого кислорода два соседних протона должны находиться в дальней позиции, а два из них - в ближней позиции, так называемые 'правила льда '. Полинг предположил, что открытая тетраэдрическая структура льда обеспечивает множество эквивалентных состояний, удовлетворяющих правилам льда.
Далее Полинг вычислил конфигурационную энтропию следующим образом: рассмотрим один моль льда, состоящий из NO и 2N протонов. Каждая связь O – O имеет два положения для протона, что приводит к двум возможным конфигурациям. Однако из 16 возможных конфигураций, связанных с каждым кислородом, только 6 являются энергетически выгодными, поддерживая ограничение молекулы H 2 O. Тогда верхняя граница чисел, которые может принимать основное состояние, оценивается как Ω < 2(6/16). Correspondingly the configurational entropy S0= k B ln (Ω) = Nk B ln (3/2) = 0,81. кал / (К · моль) = 3,4 Дж / (моль · К) удивительно согласуется с недостающей энтропией, измеренной Джиуком и Стаутом.
Хотя в расчетах Полинга не учитывались как глобальное ограничение на количество протонов, так и локальное ограничение, возникающее из-за замкнутых контуров на решетке Вюрцита, впоследствии было показано, что оценка имеет превосходную точность.
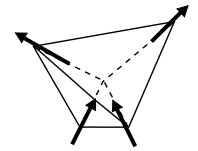Рисунок 6: Схема вращающихся молекул льда Математически аналогичная ситуация вырождению водяного льда обнаружена в спиновом льде. Обычная структура спинового льда показана на рисунке 6 в кубической структуре пирохлора с одним магнитным атомом или ионом, находящимся на каждом из четырех углов. Из-за сильного кристаллического поля в материале каждый из магнитных ионов может быть представлен дублетом основного состояния Изинга с большим моментом. Это предлагает картину спинов Изинга, находящихся на тетраэдрической решетке с общими углами, со спинами, закрепленными вдоль локальной оси квантования, кубических осей , которые совпадают с линиями, соединяющими каждую тетраэдрическую вершину с центром. Каждая тетраэдрическая ячейка должна иметь два направленных внутрь и два направленных спина, чтобы минимизировать энергию. В настоящее время модель спинового льда приближенно реализована на реальных материалах, в первую очередь на пирохлорах редкоземельных элементов Ho2Ti2O7, Dy2Ti2O7 и. Все эти материалы показывают отличную от нуля остаточную энтропию при низкой температуре.
Модель спинового льда - это лишь одно из подразделений неудовлетворенных систем. Слово разочарование было первоначально введено для описания неспособности системы одновременно минимизировать энергию конкурирующего взаимодействия между ее компонентами. В целом разочарование вызвано либо конкурирующими взаимодействиями из-за беспорядка узлов (см. Также модель Злодея, либо структурой решетки, например, в треугольной, гранецентрированной кубической (ГЦК), гексагонально-плотноупакованные, тетраэдр, пирохлор и решетки кагоме с антиферромагнитным взаимодействием. Таким образом, расстройства делятся на две категории: первая соответствует на спиновое стекло, которое имеет как беспорядок в структуре, так и фрустрацию спина; второе - геометрическое фрустрация с упорядоченной структурой решетки и фрустрация спина. Фрустрация спинового стекла понимается в рамках модель RKKY, в которой свойство взаимодействия, ферромагнитное или антиферромагнитное, зависит от расстояния между двумя магнитными ионами. Из-за беспорядка решетки в спиновом стекле один интересующий спин и его ближайшие соседи могут находиться на разных расстояниях и иметь разное взаимодействие n, что, таким образом, приводит к различному предпочтительному выравниванию спина.
С помощью методов литографии можно изготавливать магнитные островки субмикрометрового размера, геометрическое расположение которых воспроизводит фрустрацию, присущую естественным материалам спинового льда. Недавно R. F. Wang et al. сообщил об открытии искусственного геометрически фрустрированного магнита, состоящего из массивов литографически изготовленных однодоменных ферромагнитных островков. Эти острова расположены вручную, чтобы создать двумерный аналог спинового льда. Магнитные моменты упорядоченных «спиновых» островков были отображены с помощью магнитно-силовой микроскопии (MFM), а затем было тщательно изучено локальное размещение фрустрации. В своей предыдущей работе над квадратной решеткой фрустрированных магнитов они наблюдали как ледоподобные короткодействующие корреляции, так и отсутствие дальнодействующих корреляций, точно так же, как в спиновом льду при низкой температуре. Эти результаты укрепляют неизведанную основу, на которой настоящая физика разочарования может быть визуализирована и смоделирована с помощью этих искусственных геометрически фрустрированных магнитов, и вдохновляют на дальнейшую исследовательскую деятельность.
Эти искусственно разрушенные ферромагнетики могут проявлять уникальные магнитные свойства при изучении их глобального отклика на внешнее поле с использованием магнитооптического эффекта Керра. В частности, обнаружена немонотонная угловая зависимость коэрцитивной силы квадратной решетки, связанная с беспорядком в системе искусственного спинового льда.
Другой тип геометрического разочарования возникает из-за распространения местного порядка. Главный вопрос, который стоит перед физиком конденсированного состояния, - это объяснить устойчивость твердого тела.
Иногда можно установить некоторые местные правила химической природы, которые приводят к низкоэнергетическим конфигурациям и, следовательно, регулируют структурный и химический порядок. Обычно это не так, и часто локальный порядок, определяемый локальными взаимодействиями, не может свободно распространяться, что приводит к геометрическому разочарованию. Общей чертой всех этих систем является то, что даже с простыми локальными правилами они представляют большой набор, часто сложных, структурных реализаций. Геометрические расстройства играют роль в областях конденсированного состояния, от кластеров и аморфных твердых тел до сложных жидкостей.
Общий метод решения этих проблем состоит из двух этапов. Во-первых, ограничение идеального заполнения пространства снимается с учетом кривизны пространства. В этом изогнутом пространстве определена идеальная структура без фрустрации. Затем к этому идеальному шаблону применяются определенные искажения, чтобы встроить его в трехмерное евклидово пространство. Конечная структура представляет собой смесь упорядоченных областей, локальный порядок которых аналогичен порядку в шаблоне, и дефектов, возникающих в результате внедрения. Среди возможных дефектов важную роль играют дисклинации.
Разбивка плоскости на пятиугольники невозможна, но может быть реализована на сфере в форме пятиугольного додекаэдра, как показано в квазикристаллах Двухмерные примеры полезно для понимания происхождения конкуренции между местными правилами и геометрией в целом. Рассмотрим сначала расположение идентичных дисков (модель гипотетического двухмерного металла) на плоскости; мы предполагаем, что взаимодействие между дисками изотропно и локально имеет тенденцию располагать диски как можно более плотно. Наилучшее расположение трех дисков - это тривиально равносторонний треугольник с центрами дисков, расположенными в вершинах треугольника. Поэтому изучение структуры дальнего действия можно свести к изучению плоских мозаик с равносторонними треугольниками. Хорошо известное решение - треугольная мозаика с полной совместимостью локальных и глобальных правил: система называется «нефрустрированной».
Но теперь предполагается, что энергия взаимодействия будет минимальной, когда атомы находятся в вершинах правильного пятиугольника. Попытка распространить на большие расстояния упаковку этих пятиугольников, имеющих общие ребра (атомные связи) и вершины (атомы), невозможна. Это связано с невозможностью замощить плоскость правильными пятиугольниками просто потому, что угол при вершине пятиугольника не делит 2π. Три таких пятиугольника легко умещаются в общей вершине, но между двумя ребрами остается зазор. Именно такое несоответствие называется «геометрическим разочарованием». Есть один способ преодолеть эту трудность. Пусть поверхность, которую нужно выложить плиткой, не будет иметь какой-либо предполагаемой топологии, и давайте построим мозаику со строгим применением правила локального взаимодействия. В этом простом примере мы видим, что поверхность наследует топологию сферы и, следовательно, получает кривизну. Окончательная структура, в данном случае пятиугольный додекаэдр, обеспечивает идеальное распространение пятиугольного порядка. Она называется «идеальной» (бездефектной) моделью рассматриваемой конструкции.
Тетраэдрическая упаковка: двугранный угол тетраэдра не соизмерим с 2π; следовательно, остается отверстие между двумя гранями упаковки из пяти тетраэдров с общим ребром. Упаковка из двадцати тетраэдров с общей вершиной таким образом, что двенадцать внешних вершин образуют неправильный икосаэдр Стабильность металлов - давний вопрос физики твердого тела, который можно понять только в рамках квантовой механики, должным образом с учетом взаимодействия положительно заряженных ионов с валентными электронами и электронами проводимости. Тем не менее, можно использовать очень упрощенную картину металлических связей и сохранить только изотропный тип взаимодействий, что приводит к структурам, которые могут быть представлены как плотно упакованные сферы. И действительно, кристаллические простые металлические структуры часто представляют собой либо плотноупакованные гранецентрированные кубические (ГЦК), либо гексагональные плотноупакованные (ГПУ) решетки. До некоторой степени аморфные металлы и квазикристаллы также можно моделировать плотной упаковкой сфер. Локальный атомный порядок хорошо моделируется плотной упаковкой тетраэдров, что приводит к несовершенному икосаэдрическому порядку.
Правильный тетраэдр - это самая плотная конфигурация для упаковки четырех равных сфер. Таким образом, проблема плотной случайной упаковки твердых сфер может быть отображена на задаче тетраэдрической упаковки. Это практическое упражнение, чтобы попытаться упаковать мячи для настольного тенниса так, чтобы образовались только четырехгранные конфигурации. Каждый начинает с четырех шаров, расположенных в виде идеального тетраэдра, и пытается добавить новые сферы, образуя новые тетраэдры. Следующее решение с пятью шарами тривиально представляет собой два тетраэдра, имеющих общую грань; Обратите внимание, что уже с этим решением ГЦК-структура, которая содержит отдельные тетраэдрические отверстия, не показывает такой конфигурации (у тетраэдров общие ребра, а не грани). Из шести шаров построены три правильных тетраэдра, и кластер несовместим со всеми компактными кристаллическими структурами (ГЦК и ГПУ). Добавление седьмой сферы дает новый кластер, состоящий из двух «осевых» шаров, соприкасающихся друг с другом, и пяти других, соприкасающихся с последними двумя шарами, причем внешняя форма представляет собой почти правильную пятиугольную бипирамиду. Однако теперь мы сталкиваемся с реальной проблемой упаковки, аналогичной той, что встречалась выше с пятиугольной мозаикой в двух измерениях. Двугранный угол тетраэдра не соизмерим с 2π; следовательно, между двумя гранями соседних тетраэдров остается дыра. Как следствие, идеальное замощение евклидова пространства R невозможно с правильными тетраэдрами. Разочарование носит топологический характер: невозможно заполнить евклидово пространство тетраэдрами, даже сильно искаженными, если мы наложим, что постоянное количество тетраэдров (здесь пять) имеет общее ребро.
Следующий шаг имеет решающее значение: поиск нефрустрированной структуры с учетом кривизны в пространстве, чтобы локальные конфигурации распространялись одинаково и без дефектов по всему пространству.
600-ячеечный : многогранник {3,3,5} Пакет из двадцати неправильных тетраэдров с общей вершиной в таким образом, что двенадцать внешних вершин образуют правильный икосаэдр. Действительно, длина l края икосаэдра немного больше радиуса описанной сферы r (l ≈ 1.05r). Есть решение с правильными тетраэдрами, если пространство не евклидово, а сферическое. Это многогранник {3,3,5}, в нотации Шлефли, также известный как 600-ячеечный.
. Сто двадцать вершин, которые все принадлежат гиперсфере S с радиусом, равным золотому сечению (φ = 1 + √5 / 2), если ребра имеют единичную длину. Шестьсот ячеек представляют собой правильные тетраэдры, сгруппированные по пять вокруг общего ребра и по двадцать вокруг общей вершины. Эта структура называется многогранником (см. Коксетер ), что является общим названием в высшей размерности в серии, содержащей многоугольники и многогранники. Даже если эта структура встроена в четыре измерения, она рассматривается как трехмерное (искривленное) многообразие. Этот момент концептуально важен по следующей причине. Идеальные модели, представленные в искривленном пространстве, - это трехмерные искривленные шаблоны. Локально они выглядят как трехмерные евклидовы модели. Итак, многогранник {3,3,5}, который представляет собой замощение тетраэдрами, обеспечивает очень плотную атомную структуру, если атомы расположены в его вершинах. Поэтому он, естественно, используется в качестве шаблона для аморфных металлов, но не следует забывать, что это происходит за счет последовательных идеализаций.
