Pons asinorum

редактировать

Утверждение, что углы, противоположные равным сторонам равнобедренного треугольника, сами по себе равны

Pons asinorum в издании Бирна Элементов, показывающее часть доказательства Евклида.

В геометрия, утверждение, что углы, противоположные равным сторонам равнобедренного треугольника равнобедренного треугольника, сами равны, известно как pons asinorum (латинское :, английский: ), обычно переводится как «мост задниц ". Это утверждение является предложением 5 книги 1 в Elements Евклида, а также известно как теорема о равнобедренном треугольнике . Верно и обратное: если два угла треугольника равны, то и противоположные им стороны также равны. Этот термин также применяется к теореме Пифагора.

Название этого утверждения также используется метафорически для проблемы или вызова, которые отделят уверенный разум от простого, стремительного мыслителя от медленного, решительного. от более скромного, чтобы представить критический тест на способности или понимание. Его первое известное использование было в 1645 году.

Содержание

1 Доказательства
- 1.1 Евклид и Прокл
- 1.2 Папп
- 1.3 Другие
2 Во внутренних пространствах продукта
3 Этимология и родственные термины
4 Метафорическое употребление
5 Ссылки
6 Внешние ссылки

Доказательства

Доказательство Прокла

Книга 1 Евклида, утверждение 5; pons asinorum

Евклид и Прокл

Утверждение Евклида о pons asinorum включает второй вывод о том, что если равные стороны треугольника вытянуты ниже основания, то углы между удлинениями и основанием также равны равно. Доказательство Евклида включает в себя дополнительные линии этих расширений. Но, как указывает комментатор Евклида Прокл, Евклид никогда не использует второй вывод, и его доказательство можно несколько упростить, вместо этого проведя вспомогательные линии по сторонам треугольника, а остальная часть доказательства будет продолжаться более или менее. меньше так же.

Было много предположений и споров о том, почему Евклид добавил второй вывод к теореме, учитывая, что это усложняет доказательство. Одно правдоподобное объяснение, данное Проклом, состоит в том, что второй вывод может использоваться в возможных возражениях против доказательств более поздних предложений, где Евклид не охватывает все случаи. Доказательство в значительной степени опирается на то, что сегодня называется бок-угол-сторона, предыдущее предложение в Элементах.

Вариант доказательства Евклида Прокл состоит в следующем:. Пусть ABC - равнобедренный треугольник, стороны AB и AC равны. Выберите произвольную точку D на стороне AB и постройте E на AC так, чтобы AD = AE. Проведите линии BE, DC и DE.. Рассмотрим треугольники BAE и CAD; BA = CA, AE = AD, и $∠ A {\ displaystyle \ angle A}$ ${\ displaystyle \ angle A}$ равен самому себе, поэтому по схеме сторона-угол-сторона треугольники совпадают, а соответствующие стороны и углы равны равно.. Следовательно, $∠ ABE = ∠ ACD {\ displaystyle \ angle ABE = \ angle ACD}$ ${\ displaystyle \ angle ABE = \ angle ACD}$ и $∠ ADC = ∠ AEB {\ displaystyle \ angle ADC = \ angle AEB}$ ${\ displaystyle \ angle ADC = \ angle AEB}$ и BE = CD.. Поскольку AB = AC и AD = AE, BD = CE путем вычитания равных частей.. Теперь рассмотрим треугольники DBE и ECD; BD = CE, BE = CD и $∠ DBE = ∠ ECD {\ displaystyle \ angle DBE = \ angle ECD}$ ${\ displaystyle \ angle DBE = \ angle ECD}$ только что были показаны, поэтому снова применяя сторону-угол-сторону, треугольники конгруэнтны.. Следовательно, угол BDE = угол CED, а угол BED = угол CDE.. Поскольку угол BDE = угол CED и угол CDE = угол BED, угол BDC = угол CEB путем вычитания равных частей.. Рассмотрим третью пару треугольников, BDC и CEB; DB = EC, DC = EB и угол BDC = угол CEB, поэтому, применяя стороны-угол-стороны в третий раз, треугольники совпадают.. В частности, угол CBD = BCE, который необходимо было доказать.

Папп

Прокл дает гораздо более короткое доказательство, приписываемое Паппу Александрийскому. Это не только проще, но и не требует дополнительных конструкций. Метод доказательства состоит в том, чтобы нанести треугольник и его зеркальное отображение под углом. Более современные авторы, подражая методу доказательства, данному для предыдущего предложения, описывают это как поднятие треугольника, его переворачивание и возложение на себя. Чарльз Лютвидж Доджсон в Евклид и его современные соперники высмеивает этот метод, называя его «ирландским быком », потому что он явно требует, чтобы треугольник был пополам. местами сразу.

Доказательство таково:. Пусть ABC - равнобедренный треугольник, стороны которого равны AB и AC.. Рассмотрим треугольники ABC и ACB, где ACB считается вторым треугольником с вершинами A, C и B, соответствующими соответственно A, B и C в исходном треугольнике.. $∠ A {\ displaystyle \ angle A}$ ${\ displaystyle \ angle A}$ равняется самому себе, AB = AC и AC = AB, так что по стороне-углу-стороне треугольники ABC и ACB конгруэнтны.. В частности, $∠ B = ∠ C {\ displaystyle \ angle B = \ angle C}$ ${\ displaystyle \ angle B = \ angle C}$ .

Другое

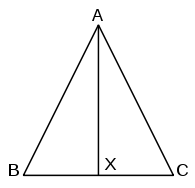Учебное доказательство

Стандартный метод учебника - построить биссектрису угла в A. Это проще, чем доказательство Евклида, но Евклид не представляет конструкции биссектрисы угла до предложения 9. Таким образом, порядок представления предложений Евклида должен быть изменен, чтобы избежать возможности круговых рассуждений.

Доказательство происходит следующим образом:. Как и раньше, пусть треугольник будет ABC с AB = AC.. Постройте биссектрису угла $∠ B A C {\ displaystyle \ angle BAC}$ $\ angle BAC$ и продолжите ее до пересечения с BC в точке X.. AB = AC и AX равен самому себе.. Кроме того, $∠ B A X = ∠ C A X {\ displaystyle \ angle BAX = \ angle CAX}$ ${\ displaystyle \ angle BAX = \ angle CAX}$ , поэтому, применяя сторону-угол-сторону, треугольник BAX и треугольник CAX конгруэнтны.. Следовательно, углы при B и C равны.

Лежандр использует аналогичную конструкцию в Éléments de géométrie, но принимает X за середину BC. Доказательство аналогично, но сторона-сторона-сторона должна использоваться вместо стороны-угла-стороны, а сторона-сторона-сторона не приводится Евклидом до тех пор, пока не появится более поздняя часть «Элементов».

Во внутренних пространствах продукта

Теорема о равнобедренном треугольнике выполняется в внутренних пространствах продукта над действительными или комплексными числами. В таких пространствах он принимает форму, которая говорит о векторах x, y и z, что если

x + y + z = 0 и ‖ x ‖ = ‖ y ‖, {\ displaystyle x + y + z = 0 { \ text {and}} \ | x \ | = \ | y \ |,}

{\ displaystyle x + y + z = 0 {\ text {and}} \ | x \ | = \ | y \ |,}

, тогда

‖ x - z ‖ = ‖ y - z ‖. {\ displaystyle \ | xz \ | = \ | yz \ |.}

{\ displaystyle \ | xz \ | = \ | yz \ |.}

Поскольку

‖ x - z ‖ 2 = ‖ x ‖ 2 - 2 x ⋅ z + ‖ z ‖ 2, {\ displaystyle \ | xz \ | ^ {2} = \ | x \ | ^ {2} -2x \ cdot z + \ | z \ | ^ {2},}

{\ displaystyle \ | xz \ | ^ {2} = \ | x \ | ^ {2} -2x \ cdot z + \ | z \ | ^ {2},}

x ⋅ z = ‖ x ‖ ‖ z ‖ соз ⁡ θ {\ displaystyle x \ cdot z = \ | x \ | \ | z \ | \ cos \ theta}

{\ displaystyle x \ cdot z = \ | x \ | \ | z \ | \ cos \ theta}

где θ - угол между двумя векторами, вывод этой пространственной формы внутреннего продукта теоремы равносильно утверждению о равенстве углов.

Этимология и связанные с ней термины

Еще одним средневековым термином pons asinorum был Элефуга, который, согласно Роджеру Бэкону, происходит от греческого elegia «страдание». ", а латинская фуга" бегство ", то есть" бегство негодяев ". Хотя эта этимология сомнительна, она перекликается с тем, что Чосер использует термин «флеминг порочных» для теоремы.

Есть два возможных объяснения названия pons asinorum, простейшее из которых что используемая диаграмма напоминает настоящий мост. Но более популярное объяснение состоит в том, что это первая настоящая проверка в Элементах интеллекта читателя и функционирует как «мост» к более сложным предложениям, которые следуют далее. Гаусс предположительно когда-то придерживался аналогичной веры в необходимость немедленного понимания личности Эйлера в качестве ориентира для того, чтобы стать первоклассным математиком.

Точно так же имя Дулкарнон было дано 47-му утверждению Книги I Евклида, более известная как теорема Пифагора, после арабского Dhū 'l qarnain ذُو ٱلْقَرْنَيْن, что означает «владелец двух рогов», поскольку диаграммы теоремы показывают два меньшие квадраты, похожие на рожки, вверху рисунка. Этот термин также используется как метафора для дилеммы. Теорема также иногда называлась «Ветряная мельница» по аналогичным причинам.

Метафорическое использование

Использование pons asinorum в качестве метафоры включает:

Филобиблон Ричарда Аунгервилля содержит отрывок «Quot Euclidis disculos retrojecit Elefuga quasi scopulos eminens et abruptus, qui nullo scalarum Suffragio scandi posset! Дурус, спрашивай, есть его sermo; quis potest eum audire?», в котором теорема сравнивается с крутой скалой, по которой никакая лестница не поможет взобраться и спрашивает, сколько потенциальных геометров отвергли.
Термин pons asinorum в обоих значениях как мост и как тест используется как метафора для нахождения среднего термина силлогизм.
Поэт 18-го века Томас Кэмпбелл написал юмористическое стихотворение под названием «Pons asinorum», в котором класс геометрии оспаривает теорему, как рота солдат может атаковать крепость; битва не обошлась без жертв.
Экономист Джон Стюарт Милль назвал Закон Рикардо основным звеном экономики
Pons Asinorum - это имя, данное конкретной конфигурации Кубика Рубика.
Эрик Рэймонд упомянул проблему синтаксически значимых пробелов в языке программирования Python в качестве основы asinorum.
финская aasinsilta и шведская åsnebrygga - это литературный прием, в котором устанавливается слабая, даже надуманная связь между двумя аргументами или темами, что почти, но не совсем non sequitur, используется как неудобный переход между ними. В серьезном тексте это считается стилистической ошибкой, поскольку он принадлежит собственно к потоку сознания - или причина письма. Типичными примерами являются завершение раздела рассказом о том, о чем идет речь в следующем разделе, без необходимости объяснять, почему темы связаны, расширение случайного упоминания до подробного рассмотрения или обнаружение надуманной связи между темами (например, «Мы купили красного вина ; говоря о красных жидкостях, завтра Всемирный день донора крови ").
В голландском ezelsbruggetje (« маленький мост ослов ») - это слово, обозначающее мнемоническое. То же самое верно и для немецкого Eselsbrücke.
В чешском oslí můstek имеет два значения - он может описывать либо надуманную связь между двумя темами, либо мнемонику.

Ссылки

^Смит, Дэвид Юджин (1925). История математики. II. Джинн и компания. стр. 284. Он образовался у моста, по которому глупцы не могли надеяться пройти, и поэтому был известен как pons asinorum, или мост глупцов.. 1. Этот термин применяется к теореме Пифагора.
^Pons asinorum - Определение и многое другое из Free Merriam
^Heath стр. 251–255
^После Прокла с. 53
^Например, Ф. Катбертсон Учебник по геометрии (Оксфорд, 1876 г.) стр. 7
^Чарльз Латвидж Доджсон, Евклид и его современные соперники Акт I Сцена II §6
^После Прокла с. 54
^Хит стр. 254 для раздела
^Например, Дж. М. Уилсон Элементарная геометрия (1878 г. Оксфорд) стр. 20
^Вслед за Уилсоном
^А. M. Legendre Éléments de géométrie (1876 Libr. De Firmin-Didot et Cie) с. 14
^Дж. Р. Ретерфорд, Гильбертово пространство, Cambridge University Press, 1993, стр. 27.
^ А. Ф. Уэст и Х. Д. Томпсон "О Дулькарноне, Элефуге и Pons Asinorum как причудливых названиях для геометрических утверждений" Бюллетень Принстонского университета Vol. 3 № 4 (1891) с. 84
^Д.Э. История математики Смита (Довер, 1958 г.) стр. 284
^Дербишир, Джон (2003). Основная одержимость: Бернхард Риман и величайшая нерешенная проблема математики. 500 Fifth Street, NW, Вашингтон, округ Колумбия, 20001: Джозеф Генри Пресс. п. 202. ISBN 0-309-08549-7. первоклассный математик.CS1 maint: location (ссылка )
^Чарльз Латвидж Доджсон, Евклид и его современные соперники Акт I, сцена II §1
^WE Aytoun (Ed.) Поэтические произведения Томаса Кэмпбелла (1864, Little, Brown) стр. 385 Google Книги
^Джон Стюарт Милль Принципы политической экономии (1866: Longmans, Green, Reader, and Дайер) Книга 2, Глава 16, стр. 261
^Рейд, Майкл (28 октября 2006 г.) «Шаблоны кубика Рубика». Www.cflmath.com. Архивировано с оригинала 12 декабря 2012 г. Дата обращения 22 сентября 2019 г.
^Эрик С. Раймонд, «Почему Python?», Linux Journal, 30 апреля 2000 г.
^Aasinsilta on laiskurin apuneuvo | Yle Uutiset | yle.fi

External ссылки

Найдите pons asinorum в Wiktionary, бесплатном словаре.

Wikisource содержит исходный текст, относящийся к этой статье: Предложение 5 элементов Евклида