Метод усреднения

В математике, более конкретно в динамических системах, то метод усреднения (также называемая теория усреднения) использует системы, содержащие разделения временных масштабов: а быстрое колебание по сравнению с медленным дрейфом. Это предполагает, что мы выполняем усреднение за заданный промежуток времени, чтобы сгладить быстрые колебания и наблюдать качественное поведение по результирующей динамике. Приближенное решение сохраняется при конечном времени, обратно пропорциональном параметру, обозначающему медленный масштаб времени. Оказывается, это обычная проблема, когда существует компромисс между тем, насколько хорошо приближенное решение сбалансировано тем, сколько времени оно остается близким к исходному решению.

Точнее, система имеет следующий вид

$${\ displaystyle \ quad {\ dot {x}} = \ varepsilon f (x, t, \ varepsilon), \ quad 0 \ leq \ varepsilon \ ll 1}$$ переменное фазовое пространство быстро колебания определяются в сравнении с медленным дрейфом в. Метод усреднения дает автономную динамическую систему ${\ displaystyle x.}$${\ displaystyle f}$ ${\ displaystyle {\ dot {x}}}$ $${\ displaystyle \ quad {\ dot {y}} = \ varepsilon {\ frac {1} {T}} \ int _ {0} ^ {T} f (y, s, 0) ~ ds =: \ varepsilon { \ bar {f}} (y)}$$ который аппроксимирует кривые решения внутри связной и компактной области фазового пространства и во времени. ${\ displaystyle {\ dot {x}}}$${\ displaystyle 1 / \ varepsilon}$

При применимости этого метода усреднения асимптотическое поведение исходной системы фиксируется динамическим уравнением для. Таким образом, качественные методы для автономных динамических систем могут быть использованы для анализа состояний

равновесия и более сложных структур, таких как медленное многообразие и инвариантные многообразия, а также их устойчивости в фазовом пространстве усредненной системы. ${\ displaystyle y}$

Кроме того, в физическом приложении было бы разумно или естественно заменить математическую модель, которая дается в форме дифференциального уравнения для, соответствующей усредненной системой, чтобы использовать усредненную систему для прогнозирования, а затем проверить предсказание по результатам физического эксперимента. ${\ displaystyle {\ dot {x}}}$${\ displaystyle {\ dot {y}}}$

Метод усреднения имеет долгую историю, которая уходит корнями в проблемы возмущений, возникшие в небесной механике (см., Например, в).

• 1 Первый пример
• 2 Определения
• 3 Теорема: усреднение в периодическом случае
  • 3.1 Замечания
  • 3.2 Стратегия доказательства
    • 3.2.1 Набросок доказательства
• 4 Неавтономный класс систем: еще примеры
  • 4.1 Замечания
  • 4.2 Пример: вводящие в заблуждение результаты усреднения
  • 4.3 Пример: уравнение Ван дер Поля
  • 4.4 Пример: ограничение временного интервала
  • 4.5 Затухающий маятник
• 5 Оценки ошибок расширения
• 6 Ссылки

Рисунок 1: Решение возмущенного уравнения логистического роста (синяя сплошная линия) и усредненного уравнения   (оранжевая сплошная линия). ${\ displaystyle {\ dot {x}} = \ varepsilon (x (1-x) + \ sin {t}) ~ x \ in \ mathbb {R}, ~ \ varepsilon = 0,05}$${\ displaystyle {\ dot {y}} = \ varepsilon y (1-y), ~ y \ in \ mathbb {R}}$

Рассмотрим нарушенный логистический рост

$${\ displaystyle \ quad {\ dot {x}} = \ varepsilon (x (1-x) + \ sin {t}) \ quad \ quad x \ in \ mathbb {R}, \ quad 0 \ leq \ varepsilon \ ll 1,}$$ и усредненное уравнение $${\ displaystyle \ quad {\ dot {y}} = \ varepsilon y (1-y) \ qquad y \ in \ mathbb {R}.}$$ Цель метода усреднения - рассказать нам о качественном поведении векторного поля, когда мы усредняем его за период времени. Это гарантирует, что решение будет аппроксимировано для времен В исключительных случаях: в этом примере приближение даже лучше, оно действительно для всех времен. Мы представляем это в разделе ниже. ${\ Displaystyle у (т)}$${\ Displaystyle х (т)}$${\ displaystyle t = {\ mathcal {O}} (1 / \ varepsilon).}$

Мы предполагаем, что векторное поле имеет

класс дифференцируемости с (или даже мы будем говорить только гладким), который мы будем обозначать. Мы разложим это зависящее от времени векторное поле в ряд Тейлора (по степеням) с остатком. Введем следующие обозначения: ${\ displaystyle f: \ mathbb {R} ^ {n} \ times \ mathbb {R} \ times \ mathbb {R} \ to \ mathbb {R} ^ {n}}$ ${\ displaystyle C ^ {r}}$${\ displaystyle r \ geq 2}$${\ displaystyle f \ in C ^ {r} (\ mathbb {R} ^ {n} \ times \ mathbb {R} \ times \ mathbb {R} ^ {+}; \ mathbb {R} ^ {n}) }$${\ Displaystyle \ varepsilon}$${\ Displaystyle е ^ {[к + 1]} (х, т, \ varepsilon)}$ $${\ Displaystyle \ четырехъядерный е (х, т, \ varepsilon) = f ^ {0} (x, t) + \ varepsilon f ^ {1} (x, t) + \ точки + \ varepsilon ^ {k} f ^ {k} (x, t) + \ varepsilon ^ {k + 1} f ^ {[k + 1]} (x, t, \ varepsilon),}$$

где - -я производная с. Поскольку нас интересуют задачи усреднения, в общем случае он равен нулю, поэтому оказывается, что нас будут интересовать векторные поля, заданные формулой ${\ displaystyle f ^ {j} = {\ frac {f ^ {(j)} (x, t, 0)} {j!}}}$${\ displaystyle j}$${\ Displaystyle 0 \ Leq J \ Leq K}$${\ displaystyle f ^ {0} (х, т)}$

$${\ Displaystyle \ четырехъядерный е (х, т, \ varepsilon) = \ varepsilon f ^ {[1]} (x, t, \ varepsilon) = \ varepsilon f ^ {1} (x, t) + \ varepsilon ^ { 2} f ^ {[2]} (x, t, \ varepsilon).}$$ Кроме того, мы определяем следующую задачу начальной стоимости в стандартной форме : $${\ displaystyle \ quad {\ dot {x}} = \ varepsilon f ^ {1} (x, t) + \ varepsilon ^ {2} f ^ {[2]} (x, t, \ varepsilon), \ qquad x (0, \ varepsilon) =: x_ {0} \ in D \ substeq \ mathbb {R} ^ {n}, \ quad 0 \ leq \ varepsilon \ ll 1.}$$

Рассмотрим для каждого связаны и ограничены, и каждый существуют и такие, что исходная система (неавтономная система динамической), задаваемое ${\ Displaystyle D \ подмножество \ mathbb {R} ^ {n}}$${\ displaystyle \ varepsilon _ {0}gt; 0}$${\ displaystyle Lgt; 0}$${\ displaystyle \ varepsilon \ leq \ varepsilon _ {0}}$

$${\ displaystyle \ quad {\ dot {x}} = \ varepsilon f ^ {1} (x, t) + \ varepsilon ^ {2} f ^ {[2]} (x, t, \ varepsilon), \ qquad x_ {0} \ in D \ substeq \ mathbb {R} ^ {n}, \ quad 0 \ leq \ varepsilon \ ll 1,}$$ имеет решение, в котором является периодическим с периодом, и оба с ограниченными на ограниченных множествах. Тогда существует постоянные такой, что решение о усредненной системе (автономная система динамической) является ${\ Displaystyle х (т, \ varepsilon)}$${\ displaystyle f ^ {1} \ in C ^ {r} (D \ times \ mathbb {R}; \ mathbb {R} ^ {n})}$ ${\ displaystyle T}$${\ displaystyle f ^ {[2]} \ in C ^ {r} (D \ times \ mathbb {R} \ times \ mathbb {R} ^ {+}; \ mathbb {R} ^ {n})}$${\ displaystyle r \ geq 2}$${\ displaystyle cgt; 0}$${\ Displaystyle у (т, \ varepsilon)}$ $${\ displaystyle \ quad {\ dot {y}} = \ varepsilon {\ frac {1} {T}} \ int _ {0} ^ {T} f ^ {1} (y, s) ~ ds =: \ varepsilon {\ bar {f}} ^ {1} (y), \ quad y (0, \ varepsilon) = x_ {0}}$$ является $${\ Displaystyle \ четырехъядерный \ | Икс (T, \ varepsilon) -y (t, \ varepsilon) \ | lt;c \ varepsilon}$$ для и. ${\ displaystyle 0 \ leq \ varepsilon \ leq \ varepsilon _ {0}}$${\ Displaystyle 0 \ Leq T \ Leq L / \ varepsilon}$

Замечания

• В этой так называемой оценке первого приближения есть два приближения: приведение векторного поля к среднему и пренебрежение членами. ${\ Displaystyle {\ mathcal {O}} (\ varepsilon ^ {2})}$
• Равномерность по отношению к начальному условию: если мы изменим, это повлияет на оценку и. Доказательство и обсуждение этого можно найти в книге Дж. Мердока. ${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle L}$${\ displaystyle c}$
• Снижение регулярности: существует более общая форма этой теоремы, которая требует только, чтобы быть

Липшица и непрерывно. Это более позднее доказательство, которое можно увидеть у Sanders et al.. Приведенная здесь формулировка теоремы основана на схеме доказательства, предложенной Крыловым-Боголюбовым, которая основана на введении преобразования, близкого к тождественному. Преимущество этого метода - расширение до более общих параметров, таких как бесконечномерные системы - уравнения в частных производных или дифференциальные уравнения с запаздыванием. ${\ displaystyle f ^ {1}}$ ${\ displaystyle f ^ {[2]}}$

Дж. Хейл представляет обобщение почти периодических векторных полей.

Стратегия доказательства

Крылов-Боголюбов понял, что медленная динамика системы определяет главный порядок асимптотического решения.

Чтобы доказать это, они предложили преобразование, близкое к тождественному, которое оказалось заменой координат с собственной шкалой времени, переводящей исходную систему в усредненную.

Набросок доказательства

1. Определение почти тождественного преобразования: гладкое отображение где предполагается достаточно регулярным и периодическим. Предлагаемое изменение координат представлено в виде. ${\ displaystyle y \ mapsto U (y, t, \ varepsilon) = y + \ varepsilon u ^ {[1]} (y, t, \ varepsilon)}$${\ displaystyle u ^ {[1]}}$${\ displaystyle T}$${\ Displaystyle х = U (у, т, \ varepsilon)}$
2. Выберите подходящий решающий

гомологическое уравнение теории усреднения:. ${\ displaystyle u ^ {[1]}}$${\ displaystyle {\ frac {\ partial u ^ {[1]}} {\ partial t}} = f ^ {1} (y, t) - {\ bar {f}} ^ {1} (y)}$

Изменение координат переводит исходную систему в ${\ displaystyle {\ dot {y}} = \ varepsilon {\ bar {f}} ^ {1} (y) + \ varepsilon ^ {2} f _ {*} ^ {[2]} (y, t, \ варепсилон).}$

Оценка ошибки из-за усечения и сравнения с исходной переменной.

В истории техники усреднения есть класс систем, которые широко изучены, и они дают нам содержательные примеры, которые мы обсудим ниже. Класс системы определяется:

$${\ displaystyle \ quad {\ ddot {z}} + z = \ varepsilon g (z, {\ dot {z}}, t), \ qquad z \ in \ mathbb {R}, \ quad z (0) = z_ {0} ~ \ mathrm {и} ~ {\ dot {z}} (0) = v_ {0},}$$

где гладко. Эта система похожа на линейную систему с небольшим нелинейным возмущением, задаваемым выражением: ${\ displaystyle g}$${\ displaystyle {\ begin {bmatrix} 0 \\\ varepsilon ~ g (z, {\ dot {z}}, t) \ end {bmatrix}}}$

$${\ displaystyle \ quad {\ begin {align} {\ dot {z_ {1}}} amp; = z_ {2}, amp; z_ {1} (0) amp; = z_ {0} \\ {\ dot {z_ {2} }}} amp; = - z_ {1} + \ varepsilon g (z_ {1}, z_ {2}, t), amp; z_ {2} (0) amp; = v_ {0}, \ end {выровнено}}}$$ отличается от стандартной формы. Следовательно, существует необходимость в явном преобразовании сделать его в стандартном виде. Мы можем изменять координаты, используя метод вариации констант. Рассмотрим невозмущенную систему, т. Е. Заданную формулой ${\ displaystyle \ varepsilon = 0}$ $${\ displaystyle {\ begin {bmatrix} {\ dot {z_ {1}}} \\ {\ dot {z_ {2}}} \ end {bmatrix}} = {\ begin {bmatrix} 0 amp; 1 \\ - 1 amp; 0 \ конец {bmatrix}} {\ begin {bmatrix} z_ {1} \\ z_ {2} \ end {bmatrix}} = A {\ begin {bmatrix} z_ {1} \\ z_ {2} \ end {bmatrix} }}$$

которая имеет фундаментальное решение, соответствующее повороту. Тогда зависящее от времени изменение координат: где - координаты, соответствующие стандартной форме. ${\ displaystyle \ Phi (t) = e ^ {At}}$${\ Displaystyle г (т) = \ фи (т) х}$${\ displaystyle x}$

Если мы возьмем производную по времени в обе стороны и обратим фундаментальную матрицу, получим

${\ displaystyle \ quad {\ dot {x}} = \ varepsilon e ^ {- At} {\ begin {bmatrix} 0 \\ ~ {\ tilde {g}} (x, {\ dot {x}}, t) \ end {bmatrix}} ~ {\ text {with}} ~ {\ tilde {g}} (x, {\ dot {x}}, t) = g (\ cos (t) x (t) + \ sin (t) {\ dot {x}} (t), - \ sin (t) x (t) + \ cos (t) {\ dot {x}} (t), t).}$

Замечания

• То же самое можно сделать с линейными частями, зависящими от времени. Хотя фундаментальное решение может быть нетривиальным для явного описания, процедура аналогична. См. Sanders et al. для получения дополнительной информации.
• Если не все собственные значения являются чисто мнимыми, это называется

условием гиперболичности. В этом случае уравнение возмущений может представлять некоторые серьезные проблемы, даже если оно ограничено, поскольку решение растет экспоненциально быстро. Однако качественно мы можем узнать асимптотическое решение, такое как результаты Хартмана-Гробмана и многое другое. ${\ displaystyle A}$ ${\ displaystyle g}$

Иногда, чтобы получить стандартные формы, с которыми легче работать, мы можем выбрать вращающийся набор координат системы отсчета - полярные координаты - которые также определяют начальное условие и определяют систему: ${\ Displaystyle Z_ {1} = r \ sin (t- \ phi) ~ \ mathrm {и} ~ z_ {2} = r \ cos (t- \ phi)}$${\ Displaystyle (г (0), \ фи (0))}$

$${\ displaystyle \ quad {\ begin {bmatrix} {\ dot {r}} \\ {\ dot {\ phi}} \ end {bmatrix}} = \ varepsilon {\ begin {bmatrix} \ cos (t- \ phi) g (r \ sin (t- \ phi), r \ cos (t- \ phi), t) \\ {\ frac {1} {r}} \ sin (t- \ phi) g (r \ sin (t- \ phi), r \ cos (t- \ phi), t) \ end {bmatrix}}.}$$ Если мы усредним его до тех пор, пока окрестности начала координат исключены (поскольку полярные координаты не работают), получаем: ${\ displaystyle g \ in C ^ {1}}$ $${\ displaystyle \ quad {\ begin {array} {lcr} {\ bar {f}} _ {1} ^ {1} (r) = {\ frac {1} {2 \ pi}} \ int _ {0 } ^ {2 \ pi} \ cos (s- \ phi) g (r \ sin (s- \ phi), r \ cos (s- \ phi), s) ds \\ {\ bar {f}} _ {2} ^ {1} (r) = {\ frac {1} {2 \ pi r}} \ int _ {0} ^ {2 \ pi} \ sin (s- \ phi) g (r \ sin ( s- \ phi), r \ cos (s- \ phi), s) ds, \ end {array}}}$$ где усредненная система $${\ displaystyle \ quad {\ begin {array} {lcr} {\ dot {\ bar {r}}} = \ varepsilon {\ bar {f}} _ {1} ^ {1} ({\ bar {r} }) \\ {\ dot {\ bar {\ phi}}} = \ varepsilon {\ bar {f}} _ {2} ^ {1} ({\ bar {r}}) \ end {array}}. }$$

Пример: вводящие в заблуждение результаты усреднения

Рисунок 2: Простой гармонический осциллятор с малым периодическим демпфирующим членом, заданным как. Численное моделирование исходного уравнения (синяя сплошная линия) сравнивается с системой усреднения (оранжевая пунктирная линия) и грубой усредненной системой (зеленая пунктирная линия). Левый график отображает решение, эволюционировавшее во времени, а правый график представляет собой фазовое пространство. Отметим, что грубое усреднение не соответствует ожидаемому решению. ${\ displaystyle {\ ddot {z}} + 4 \ varepsilon \ cos ^ {2} {(t)} {\ dot {z}} + z = 0, ~ z (0) = 0, ~ {\ dot { z}} (0) = 1; ~ \ varepsilon = 0,05}$

Метод содержит некоторые предположения и ограничения. Эти ограничения играют важную роль, когда мы усредняем исходное уравнение, которое не имеет стандартной формы, и мы можем обсудить контрпример к нему. Следующий пример, чтобы воспрепятствовать этому поспешному усреднению:

$${\ displaystyle \ quad {\ ddot {z}} + 4 \ varepsilon \ cos ^ {2} {(t)} {\ dot {z}} + z = 0, \ quad \ quad z (0) = 0, \ quad {\ dot {z}} (0) = 1,}$$ где мы положили в соответствии с предыдущими обозначениями. ${\ Displaystyle г (г, {\ точка {z}}, т) = - 4 \ соз ^ {2} (т) {\ точка {z}}}$

Эта система соответствует затухающему гармоническому осциллятору, где демпфирующий член колеблется между и. Усреднение члена трения за один цикл дает уравнение: ${\ displaystyle 0}$${\ displaystyle 4 \ varepsilon}$${\ displaystyle 2 \ pi}$

$${\ displaystyle \ quad {\ ddot {\ bar {z}}} + 2 \ varepsilon {\ dot {\ bar {z}}} + {\ bar {z}} = 0, \ quad \ quad {\ bar { z}} (0) = 0, \ quad {\ dot {\ bar {z}}} (0) = 1.}$$ Решение $${\ displaystyle {\ bar {z}} (t) = {\ frac {1} {(1- \ varepsilon ^ {2}) ^ {\ frac {1} {2}}}} e ^ {- \ varepsilon t} \ sin {((1- \ varepsilon ^ {2}) ^ {\ frac {1} {2}} t)}.}.$$ скорость сходимости к началу координат. Усредненная система, полученная из стандартной формы, дает: ${\ Displaystyle \ varepsilon}$ $${\ displaystyle \ quad {\ begin {array} {lcr} {\ dot {\ bar {r}}} = - {\ frac {1} {2}} \ varepsilon {\ bar {r}} (2+ \ cos (2 {\ bar {\ phi}})), ~ {\ bar {r}} (0) = 1 \\ {\ dot {\ bar {\ phi}}} = {\ frac {1} {2 }} \ varepsilon \ sin (2 {\ bar {\ phi}}), ~ {\ bar {\ phi}} (0) = 0, \ end {array}}}$$ что в прямоугольной координате явно показывает, что действительно скорость сходимости к началу координат отличается от предыдущей грубой усредненной системы: ${\ displaystyle {\ frac {3} {2}} \ varepsilon}$ $${\ displaystyle \ quad y (t) = e ^ {- {\ frac {3} {2}} \ varepsilon t} \ sin {t}}$$

Пример: уравнение Ван дер Поля

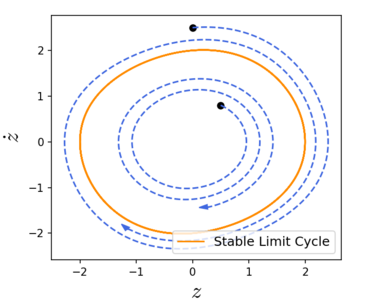
Рисунок 3: Фазовое пространство генератора Ван дер Поля с. Устойчивый предельный цикл (оранжевая сплошная линия) в системе правильно фиксируется качественным анализом усредненной системы. Для двух разных начальных условий (черные точки) мы наблюдаем траектории (пунктирная синяя линия), сходящиеся к периодической орбите. ${\ displaystyle \ varepsilon = 0,1}$

Ван дер Поль был озабочен получением приближенного решения для уравнений типа

$${\ displaystyle \ quad {\ ddot {z}} + \ varepsilon (1-z ^ {2}) {\ dot {z}} + z = 0,}$$ где следуют предыдущим обозначениям. Эта система называется осциллятором Ван дер Поля. Если мы применим периодическое усреднение к этому нелинейному осциллятору, это даст нам качественное знание фазового пространства без явного решения системы. ${\ Displaystyle г (г, {\ точка {z}}, т) = (1-z ^ {2}) {\ точка {z}}}$

Усредненная система

$${\ displaystyle \ quad {\ begin {array} {lcr} {\ dot {\ bar {r}}} = {\ frac {1} {2}} \ varepsilon {\ bar {r}} (1 - {\ frac {1} {4}} {\ bar {r}} ^ {2}) \\ {\ dot {\ bar {\ phi}}} = 0, \ end {array}}}$$ и мы можем проанализировать неподвижные точки и их устойчивость. В начале координат имеется неустойчивая неподвижная точка и устойчивый предельный цикл, представленный символом. ${\ displaystyle {\ bar {r}} = 2}$

Существование такого устойчивого предельного цикла можно сформулировать в виде теоремы.

Теорема (Существование периодической орбиты) : Если - гиперболическая неподвижная точка ${\ displaystyle p_ {0}}$

$${\ displaystyle \ quad {\ dot {y}} = \ varepsilon {\ bar {f}} ^ {1} (y)}$$ Тогда существует такое, что для всех, ${\ displaystyle \ varepsilon _ {0}gt; 0}$${\ displaystyle 0 lt;\ varepsilon lt;\ varepsilon _ {0}}$ $${\ displaystyle \ quad {\ dot {x}} = \ varepsilon f ^ {1} (x, t) + \ varepsilon ^ {2} f ^ {[2]} (x, t, \ varepsilon)}$$ имеет единственную гиперболическую периодическую орбиту того же типа устойчивости, что и. ${\ Displaystyle \ гамма _ {\ varepsilon} (т) = p_ {0} + {\ mathcal {O}} (\ varepsilon)}$${\ displaystyle p_ {0}}$

Доказательства можно найти у Гукенхаймера и Холмса, Сандерса и др. и для углового корпуса в Chicone.

Пример: ограничение временного интервала

Рисунок 4: График изображает две фундаментальные величины, на которых основан метод усреднения: ограниченная и связная область фазового пространства и продолжительность действия усредненного решения (определяемая константой). В этом случае. Обратите внимание, что оба решения взорвутся за конечное время. Следовательно, было выбрано соответственно, чтобы сохранить ограниченность решения, и временной интервал применимости приближения составляет. ${\ displaystyle D}$${\ displaystyle c}$${\ textstyle {\ ddot {z}} + z = 8 \ varepsilon \ cos {(t)} {\ dot {z}} ^ {2}, ~ z (0) = 0, ~ {\ dot {z} } (0) = 1; ~ 8 \ varepsilon = {\ frac {2} {15}}}$${\ displaystyle D}$${\ Displaystyle 0 \ Leq \ varepsilon т lt;L lt;{\ гидроразрыва {1} {3}}}$

Теорема о среднем предполагает наличие связной и ограниченной области, которая влияет на временной интервал достоверности результата. Следующий пример указывает на это. Рассмотрим ${\ Displaystyle D \ подмножество \ mathbb {R} ^ {n}}$${\ displaystyle L}$

$${\ displaystyle \ quad {\ ddot {z}} + z = 8 \ varepsilon \ cos {(t)} {\ dot {z}} ^ {2}, ~ z (0) = 0, ~ {\ dot { z}} (0) = 1,}$$ где. Усредненная система состоит из ${\ displaystyle g (z, {\ dot {z}}, t) = 8 {\ dot {z}} ^ {2} \ cos (t)}$ $${\ displaystyle \ quad {\ begin {array} {lcr} {\ dot {\ bar {r}}} = 3 \ varepsilon {\ bar {r}} ^ {2} \ cos ({\ bar {\ phi} }), ~ {\ bar {r}} (0) = 1 \\ {\ dot {\ bar {\ phi}}} = - \ varepsilon {\ bar {r}} \ sin ({\ bar {\ phi }}), ~ {\ bar {\ phi}} (0) = 0, \ end {array}}}$$ что при этом начальном условии указывает, что исходное решение ведет себя как $${\ displaystyle \ quad z (t) = {\ frac {\ sin (t)} {1-3 \ varepsilon t}} + {\ mathcal {O}} (\ varepsilon),}$$ где он держится на ограниченной области над. ${\ Displaystyle 0 \ Leq \ varepsilon т \ Leq L lt;{\ гидроразрыва {1} {3}}}$

Затухающий маятник

Рассмотрим демпфированный маятник, точка подвеса которого колеблется вертикально под действием высокочастотного сигнала небольшой амплитуды (обычно это называется дизерингом ). Уравнение движения такого маятника имеет вид

${\ Displaystyle м (l {\ ddot {\ theta}} - ak \ omega ^ {2} \ sin \ omega t \ sin \ theta) = - mg \ sin \ theta -k (l {\ dot {\ theta}) } + a \ omega \ cos \ omega t \ sin \ theta)}$

где описывает движение точки подвеса, описывает затухание маятника, - угол, образованный маятником с вертикалью. ${\ Displaystyle а \ грех \ омега т}$${\ displaystyle k}$${\ displaystyle \ theta}$

Фазовое пространство форма этого уравнения дается формулой

${\ displaystyle {\ begin {align} {\ dot {t}} amp; = 1 \\ {\ dot {\ theta}} amp; = p \\ {\ dot {p}} amp; = {\ frac {1} { ml}} (mak \ omega ^ {2} \ sin \ omega t \ sin \ theta -mg \ sin \ theta -k (lp + a \ omega \ cos \ omega t \ sin \ theta)) \ end {выровнено} }}$

где мы ввели переменную и записали систему как

автономную систему первого порядка в -пространстве. ${\ displaystyle p}$${\ Displaystyle (т, \ тета, р)}$

Предположим, что угловая частота вертикальных колебаний,, гораздо больше, чем собственная частота маятника,. Предположим также, что амплитуда вертикальных колебаний много меньше длины маятника. Траектория маятника в фазовом пространстве будет описывать

спираль вокруг кривой, двигаясь с медленной скоростью, но перемещаясь вокруг нее с большой скоростью. Радиус спирали вокруг будет мал и пропорционален. Среднее поведение траектории в масштабе времени, намного превышающем, будет следовать кривой. ${\ displaystyle \ omega}$${\ displaystyle {\ sqrt {g / l}}}$${\ displaystyle a}$${\ displaystyle l}$ ${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle {\ sqrt {g / l}}}$${\ displaystyle \ omega}$${\ displaystyle C}$${\ displaystyle a}$${\ displaystyle 2 \ pi / \ omega}$${\ displaystyle C}$

Методика усреднения для задач с начальным значением до сих пор обрабатывалась оценками ошибок достоверности порядка. Однако бывают обстоятельства, при которых оценки можно продлить на большее время, даже на все времена. Ниже мы имеем дело с системой, содержащей асимптотически устойчивую неподвижную точку. Такая ситуация повторяет то, что показано на рисунке 1. ${\ displaystyle 1 / \ varepsilon}$

Теорема (Экхаус / Санчес-Паленсия ) Рассмотрим задачу начального значения

$${\ displaystyle \ quad {\ dot {x}} = \ varepsilon f ^ {1} (x, t), \ qquad x_ {0} \ in D \ substeq \ mathbb {R} ^ {n}, \ quad 0 \ leq \ varepsilon \ ll 1.}$$ Предполагать $${\ displaystyle \ quad {\ dot {y}} = \ varepsilon \ lim _ {T \ to \ infty} {\ frac {1} {T}} \ int _ {0} ^ {T} f ^ {1} (y, s) ~ ds =: \ varepsilon {\ bar {f}} ^ {1} (y), \ quad y (0, \ varepsilon) = x_ {0}}$$ существует и содержит асимптотически устойчивую неподвижную точку в линейном приближении. Кроме того, непрерывно дифференцируем по in и имеет область притяжения. Для любого компакта и для всех ${\ displaystyle y = 0}$${\ displaystyle {\ bar {f}} ^ {1}}$${\ displaystyle y}$${\ displaystyle D}$${\ displaystyle D ^ {0} \ subset D}$${\ Displaystyle К \ подмножество D ^ {0}}$${\ displaystyle x_ {0} \ in K}$ $${\ displaystyle \ quad \ | x (t) -y (t) \ | = {\ mathcal {O}} (\ delta (\ varepsilon)), \ quad 0 \ leq t lt;\ infty,}$$

с в общем случае и в периодическом случае. ${\ Displaystyle \ дельта (\ varepsilon) = о (1)}$${\ Displaystyle {\ mathcal {O}} (\ varepsilon)}$